2_Pryamye_i_ploskosti_2022-2_2

1.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
ГЕОМЕТРИЧЕСКИЕ МОДЕЛИ ПРЯМЫХ И ПЛОСКОСТЕЙ
ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ПРЯМЫХ
L t A a t
ЛЮБАЯ ПРЯМАЯ ЛИНИЯ
МОЖЕТ БЫТЬ ОПРЕДЕЛЕНА
t>1
ДВУМЯ ТОЧКАМИ.
ОНА ПРОХОДИТ ЧЕРЕЗ НИХ
L(t) ПОЛОЖЕНИЕ ТОЧКИ
НА ПРЯМОЙ,
И ПРОДОЛЖАЕТСЯ
СООТВЕТСТВУЮЩЕЕ
В ОБОИХ
B (t=1)
ПАРАМЕТРУ t
НАПРАВЛЕНИЯХ
ОСНОВНЫЕ
ФОРМЫ
ПРЕДСТАВЛЕНИЯ
ПРЯМОЙ
a ( B A ) t 0 , 1
A (t=0)
t<0
1. ДВУХТОЧЕЧНОЕ
ПРЕДСТАВЛЕНИЕ ПРЯМОЙ
2. ПАРАМЕТРИЧЕСКОЕ
ПРЕДСТАВЛЕНИЕ ПРЯМОЙ
3.ТОЧЕЧНАЯ НОРМАЛЬНАЯ
ФОРМА ПРЯМОЙ
t
0
,
L t t 0 L 0 A
t 1,
L t t 1 L 1 B
t ,
ПАРАМЕТРИЧЕСКОЕ
ПРЕДСТАВЛЕНИЕ
L t A a t
ПРЯМОЙ

2.

ГМ в САПР. ПРЯМЫЕ
И ПЛОСКОСТИ
ПРИМЕР
1
НАЙТИ ПАРАМЕТРИЧЕСКУЮ ФОРМУ
ПРЯМОЙ,
ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ НА
ПЛОСКОСТИ:
A = (3, 5), В = (2, 7).
a B A 1, 2
L(t ) A a t 3 t , 5 2t
ПРИМЕР 2
НАЙТИ ПАРАМЕТРИЧЕСКУЮ ФОРМУ
ПРОСТРАНСТВЕННОЙ ПРЯМОЙ, ПРОХОДЯЩЕЙ
ЧЕРЕЗ ТОЧКИ : A = (3, 5, 6), В = (2, 7, 3).
a B A 1, 2, 3
L(t ) A a t 3 t , 5 2t ,6 3t

3.

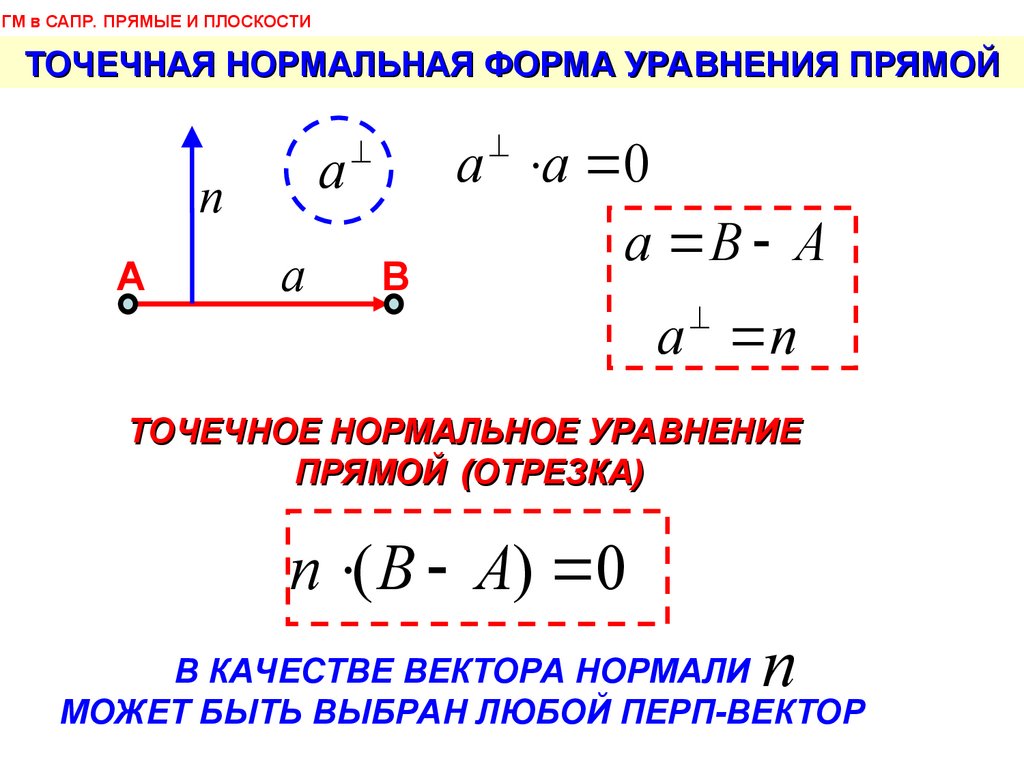
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
ТОЧЕЧНАЯ НОРМАЛЬНАЯ ФОРМА УРАВНЕНИЯ ПРЯМОЙ
n
A
a
a
B
a a 0
a B A
a n
ТОЧЕЧНОЕ НОРМАЛЬНОЕ УРАВНЕНИЕ
ПРЯМОЙ (ОТРЕЗКА)
n ( B A) 0
В КАЧЕСТВЕ ВЕКТОРА НОРМАЛИ n
МОЖЕТ БЫТЬ ВЫБРАН ЛЮБОЙ ПЕРП-ВЕКТОР

4.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
ПРИМЕР
ДЛЯ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТОЧКИ НА ПЛОСКОСТИ
ПОСТРОИТЬ
a B A ( 2 , 6 )
A = (3, 4), В = (5, -2)
ТОЧЕЧНУЮ НОРМАЛЬНУЮ ФОРМУ
n a ( a y , a x ) (6, 2)
ВЫБЕРЕМ В КАЧЕСТВЕ ПРОИЗВОЛЬНОЙ ТОЧКИ ПРЯМОЙ,
n
ТОЧКУ A = (3, 4), ТОГДА ИЗ ( B A) 0 ПОЛУЧИМ:
n a (6, 2) ( x, y ) (3, 4) 0
6 x 2 y 26 (*)
ОБЕ ЧАСТИ (*) МОЖНО РАЗДЕЛИТЬ НА 26
ИЛИ ЛЮБОЕ ДРУГОЕ ЧИСЛО ОТЛИЧНОЕ ОТ 0
ФОРМЫ В КАЧЕСТВЕ ВЕКТОРА n МОЖЕТ
ВЫСТУПАТЬ
ЛЮБОЙ ВЕКТОР, ПОЛУЧЕННЫЙ ИЗ a УМНОЖЕНИЕМ
СЛЕДОВАТЕЛЬНО ДЛЯ ПОСТРОЕНИЯ ТОЧЕЧНОЙ НОРМАЛЬНОЙ
ЕГО НА МАСШТАБИРУЮЩИЙ СКАЛЯР

5.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
СЛЕДОВАТЕЛЬНО НОРМАЛЬ К ПРЯМОЙ,
ПРЯМОЙ ЗАДАННОЙ
ОБЩИМ УРАВНЕНИЕМ ПРЯМОЙ ЛИНИИ НА ПЛОСКОСТИ
A x B y C 0
МОЖНО ПОЛУЧИТЬ СЛЕДУЮЩИМ ОБРАЗОМ:
A x B y C 0
f x g y 1
( f , g ) ( x, y ) 1
СЛЕДОВАТЕЛЬНО n ( f , g )
РАССМОТРИМ СВЯЗЬ МЕЖДУ ПАРАМЕТРИЧЕСКОЙ
ФОРМОЙ ПРЯМОЙ И ЕЁ ТОЧЕЧНОЙ НОРМАЛЬНОЙ ФОРМОЙ
L(t ) A a t
n a a
a n
ПАРАМЕТРИЧЕСКОЕ
ОПИСАНИЕ ПРЯМОЙ
ТАК КАК a n
ПАРАМЕТРИЧЕСКОЕ
ОПИСАНИЕ ПРЯМОЙ
ЧЕРЕЗ ВЕКТОР НОРМАЛИ
L(t ) A n t

6.

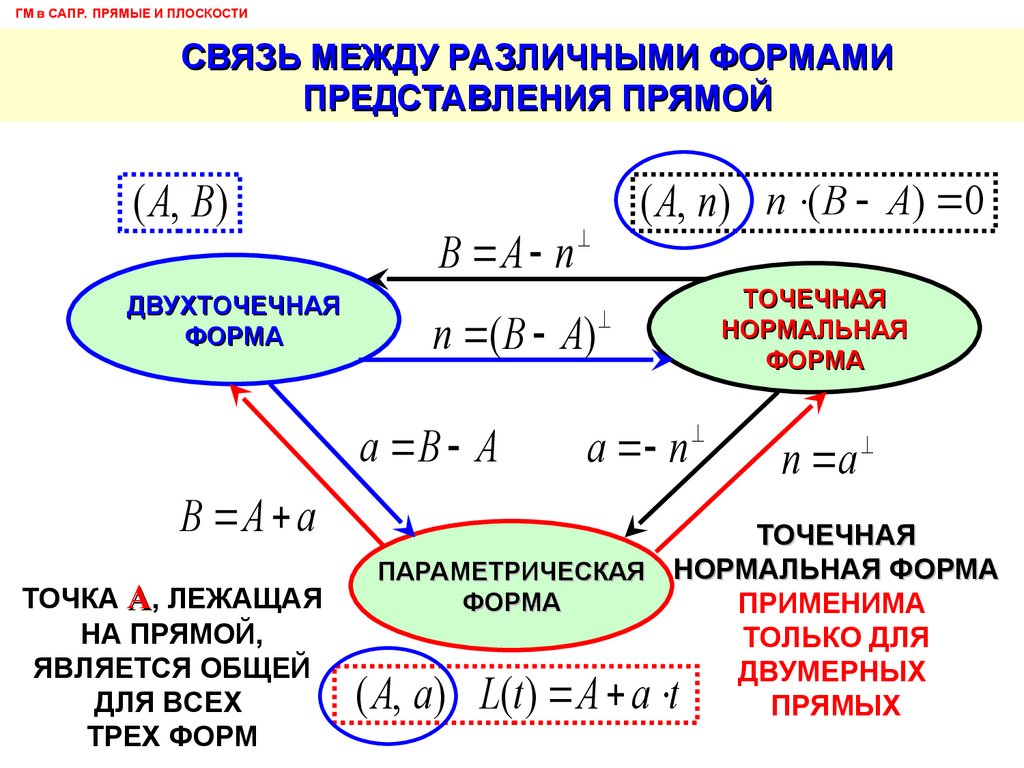
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
СВЯЗЬ МЕЖДУ РАЗЛИЧНЫМИ ФОРМАМИ
ПРЕДСТАВЛЕНИЯ ПРЯМОЙ
( A, B)
ДВУХТОЧЕЧНАЯ
ФОРМА
B A a
ТОЧКА А, ЛЕЖАЩАЯ
НА ПРЯМОЙ,
ЯВЛЯЕТСЯ ОБЩЕЙ
ДЛЯ ВСЕХ
ТРЕХ ФОРМ
B A n
n ( B A)
a B A
( A, n ) n ( B A) 0
a n
ТОЧЕЧНАЯ
НОРМАЛЬНАЯ
ФОРМА
n a
ТОЧЕЧНАЯ
ПАРАМЕТРИЧЕСКАЯ НОРМАЛЬНАЯ ФОРМА
ФОРМА
ПРИМЕНИМА
ТОЛЬКО ДЛЯ
ДВУМЕРНЫХ
ПРЯМЫХ
( A, a ) L(t ) A a t

7.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
МОДЕЛИ ПЛОСКОСТЕЙ В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
ПЛОСКОСТЬ — ОДНО ИЗ ФУНДАМЕНТАЛЬНЫХ ПОНЯТИЙ
В КОМПЬЮТЕРНОЙ ГРАФИКЕ
ПОДОБНО ПРЯМЫМ, ОНА ИМЕЕТ ТРИ ОСНОВНЫЕ ФОРМЫ
ОСНОВНЫЕ
ФОРМЫ
ПЛОСКОСТИ
1. ТРЕХТОЧЕЧНАЯ ФОРМА
2. ПАРАМЕТРИЧЕСКАЯ ФОРМА
3.ТОЧЕЧНАЯ НОРМАЛЬНАЯ ФОРМА
1. ТРЕХТОЧЕЧНАЯ ФОРМА ПЛОСКОСТИ
A
C
ЧЕРЕЗ ТРИ ТОЧКИ, НЕ ЛЕЖАЩИЕ НА ОДНОЙ ПРЯМОЙ,
ПРЯМОЙ
ПРОХОДИТ ПЛОСКОСТЬ И ПРИТОМ ТОЛЬКО ОДНА
B
ЭТА АКСИОМА ОДНОЗНАЧНО ОПРЕДЕЛЯЕТ
ПЛОСКОСТЬ С ПОМОЩЬЮ ЛЮБЫХ ТРЁХ ЕЁ ТОЧЕК,
НЕ ЛЕЖАЩИХ НА ОДНОЙ ПРЯМОЙ.
ПОЭТОМУ ПЛОСКОСТЬ МОЖНО ЗАДАВАТЬ
НЕ ЛЕЖАЩИМИ НА ОДНОЙ ПРЯМОЙ ТРЕМЯ ТОЧКАМИ

8.

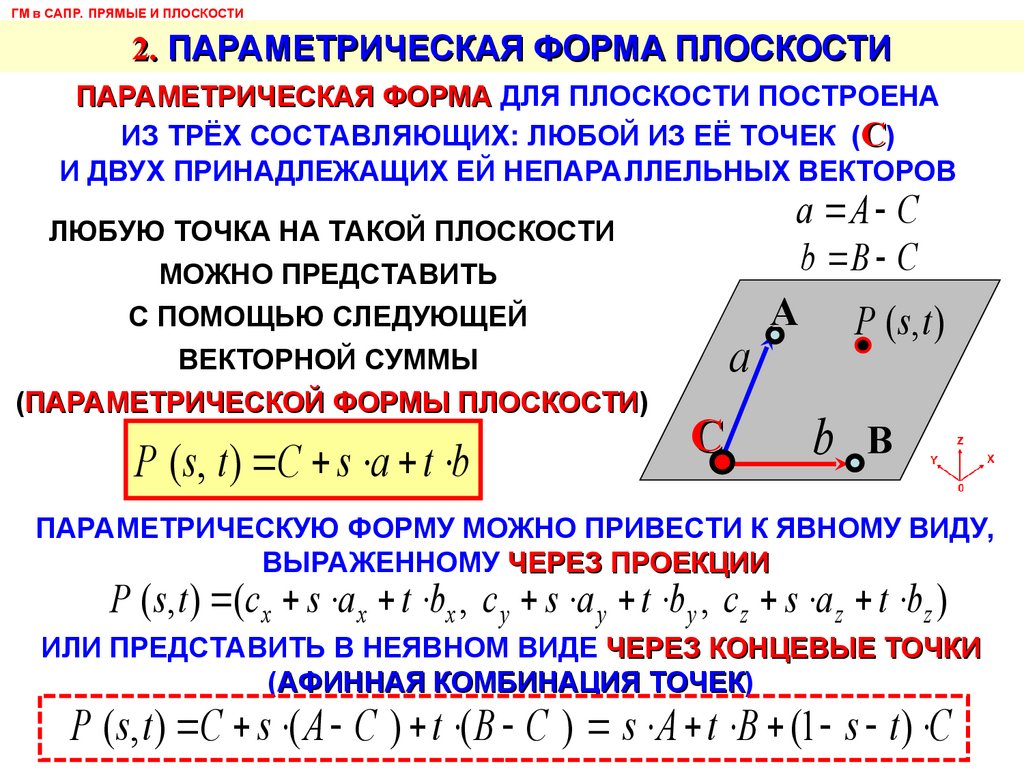
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
2. ПАРАМЕТРИЧЕСКАЯ ФОРМА ПЛОСКОСТИ
ПАРАМЕТРИЧЕСКАЯ ФОРМА ДЛЯ ПЛОСКОСТИ ПОСТРОЕНА
ИЗ ТРЁХ СОСТАВЛЯЮЩИХ: ЛЮБОЙ ИЗ ЕЁ ТОЧЕК (С)
И ДВУХ ПРИНАДЛЕЖАЩИХ ЕЙ НЕПАРАЛЛЕЛЬНЫХ ВЕКТОРОВ
ЛЮБУЮ ТОЧКА НА ТАКОЙ ПЛОСКОСТИ
МОЖНО ПРЕДСТАВИТЬ
С ПОМОЩЬЮ СЛЕДУЮЩЕЙ
ВЕКТОРНОЙ СУММЫ
(ПАРАМЕТРИЧЕСКОЙ ФОРМЫ ПЛОСКОСТИ)
ПЛОСКОСТИ
P ( s, t ) C s a t b
a A C
b B C
A
a
C
P ( s, t )
b B
ПАРАМЕТРИЧЕСКУЮ ФОРМУ МОЖНО ПРИВЕСТИ К ЯВНОМУ ВИДУ,
ВЫРАЖЕННОМУ ЧЕРЕЗ ПРОЕКЦИИ
P ( s, t ) (c x s a x t bx , c y s a y t by , c z s a z t bz )
ИЛИ ПРЕДСТАВИТЬ В НЕЯВНОМ ВИДЕ ЧЕРЕЗ КОНЦЕВЫЕ ТОЧКИ
(АФИННАЯ КОМБИНАЦИЯ ТОЧЕК)
ТОЧЕК
P ( s, t ) C s ( A C ) t ( B C ) s A t B (1 s t ) C

9.

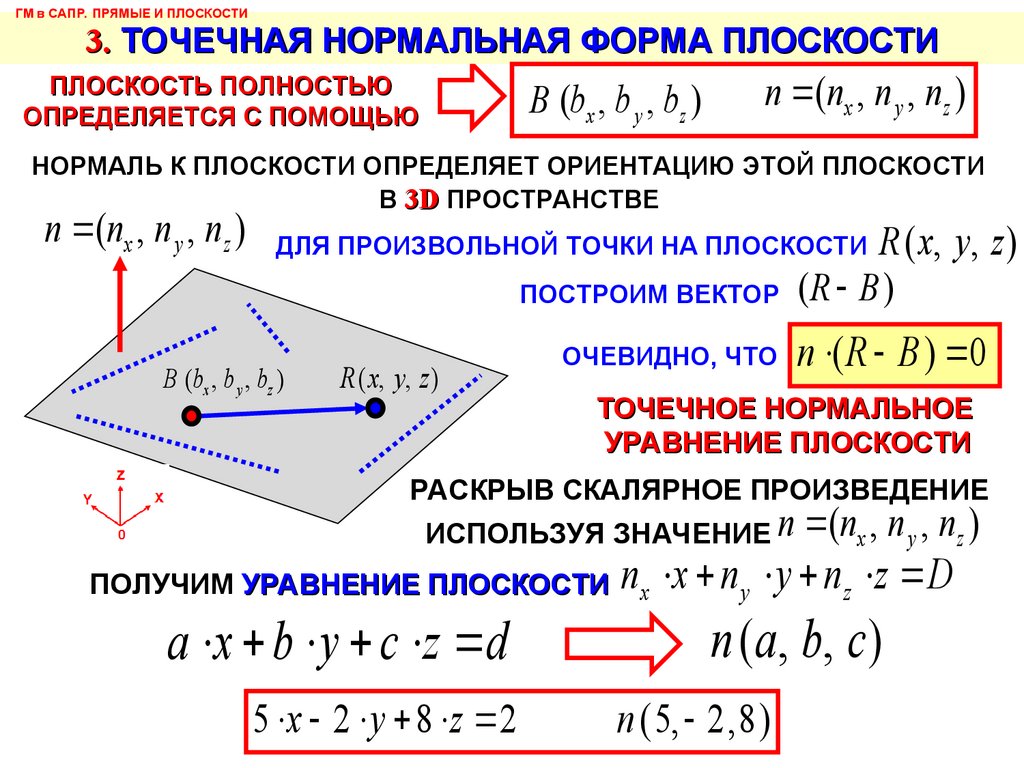
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
3. ТОЧЕЧНАЯ НОРМАЛЬНАЯ ФОРМА ПЛОСКОСТИ
ПЛОСКОСТЬ ПОЛНОСТЬЮ
ОПРЕДЕЛЯЕТСЯ С ПОМОЩЬЮ
B (bx , b y , bz )
n (nx , n y , nz )
НОРМАЛЬ К ПЛОСКОСТИ ОПРЕДЕЛЯЕТ ОРИЕНТАЦИЮ ЭТОЙ ПЛОСКОСТИ
В 3D ПРОСТРАНСТВЕ
n (nx , n y , nz )
ДЛЯ ПРОИЗВОЛЬНОЙ ТОЧКИ НА ПЛОСКОСТИ
ПОСТРОИМ ВЕКТОР
B (bx , b y , bz )
R ( x, y , z )
R ( x, y , z )
(R B )
ОЧЕВИДНО, ЧТО n ( R B ) 0
ТОЧЕЧНОЕ НОРМАЛЬНОЕ
УРАВНЕНИЕ ПЛОСКОСТИ
РАСКРЫВ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
ИСПОЛЬЗУЯ ЗНАЧЕНИЕ n ( nx , n y , nz )
ПОЛУЧИМ УРАВНЕНИЕ ПЛОСКОСТИ nx x n y y n z z D
a x b y c z d
5 x 2 y 8 z 2
n ( a , b, c )
n ( 5, 2 , 8 )

10.

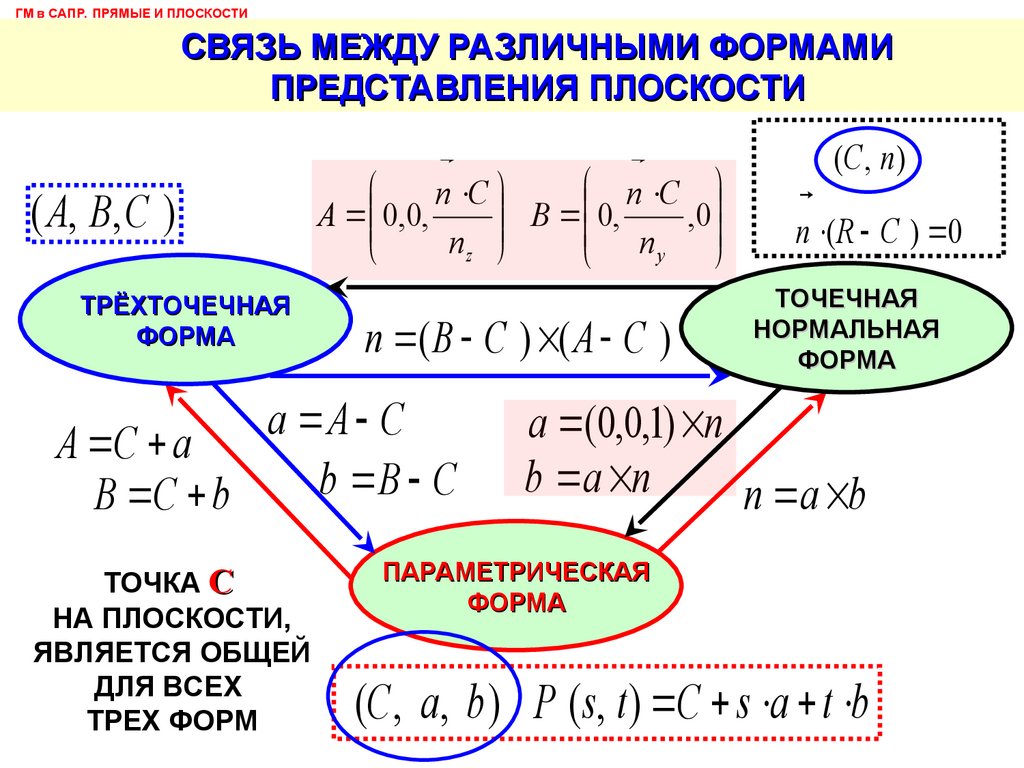
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
СВЯЗЬ МЕЖДУ РАЗЛИЧНЫМИ ФОРМАМИ
ПРЕДСТАВЛЕНИЯ ПЛОСКОСТИ
( A, B, C )
ТРЁХТОЧЕЧНАЯ
ФОРМА
n С
n С
B 0,
A 0,0,
,0
n
n
z
y
n ( B C ) ( A C )
a A C
A C a
b B С
B C b
ТОЧКА С
НА ПЛОСКОСТИ,
ЯВЛЯЕТСЯ ОБЩЕЙ
ДЛЯ ВСЕХ
ТРЕХ ФОРМ
(C , n )
n ( R C ) 0
ТОЧЕЧНАЯ
НОРМАЛЬНАЯ
ФОРМА
a (0,0,1) n
b a n
n a b
ПАРАМЕТРИЧЕСКАЯ
ФОРМА
(C , a, b ) P ( s, t ) C s a t b

11.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
a (0, 0,1) n b a n
ИМЕЯ НОРМАЛЬ n К ПЛОСКОСТИ ТРЕБУЕТСЯ
a Иb ,
НАЙТИ ДВА НЕКОЛЛИНЕАРНЫХ ВЕКТОРА
КОТОРЫЕ ПЕРПЕНДИКУЛЯРНЫ n ( nx , n y , nz )
n
ИСПОЛЬЗУЕМ ТО ОБСТОЯТЕЛЬСТВО, ЧТО ВЕКТОРНОЕ
ПРОИЗВЕДЕНИЕ ЛЮБОГО ВЕКТОРА НА
ПЕРПЕНДИКУЛЯРНО К
n.
ВЫБЕРЕМ ПРОСТЕЙШИЙ ВЕКТОР, НАПРИМЕР (0, 0,1) , И ПОСТРОИМ
a
a (0, 0,1) n n y , nx ,0
a n
n
КАК ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ЭТОГО ВЕКТОРА НА
b
n a
b a; b n
:
ИСПОЛЬЗУЕМ ЭТУ ЖЕ ИДЕЮ ДЛЯ ФОРМИРОВАНИЯ
ВЕКТОРА , НОРМАЛЬНОГО К ВЕКТОРАМ
И :
b n a nx nz , n y nz , nx2 n 2y

12.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
n С
n С
B 0,
A 0,0,
,0
n
n
z
y
ТАК КАК, ТОЧКА C УЖЕ ИЗВЕСТНА. ОСТАВШИЕСЯ ДВЕ ТОЧКИ
МОЖНО НАЙТИ ПРИ ПОМОЩИ КОНКРЕТНЫХ ЗНАЧЕНИЙ
САМОЙ
ТОЧЕЧНОЙ НОРМАЛЬНОЙ ФОРМЫ n ( R C ) 0
nx x n y y nz z n C
(1)
ВЫБЕРЕМ ТОЧКУ НА ПЛОСКОСТИ A 0 , 0 , a z
n C
ИЗ УРАВНЕНИЯ (1) НАХОДИМ a z
nz
АНАЛОГИЧНО ВЫБЕРЕМ ТОЧКУ B 0 , b y , 0
n C
ДЛЯ НАХОЖДЕНИЯ by
ny

13.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
ПРИМЕР
ТОЧКА B С КООРДИНАТАМИ (1, 2, 3)
3 ПРИНАДЛЕЖИТ
ПЛОСКОСТИ С НОРМАЛЬЮ (2, -1, -2).
-2)
ОПРЕДЕЛИТЬ ТОЧЕЧНУЮ НОРМАЛЬНУЮ ФОРМУ
И УРАВНЕНИЕ ПЛОСКОСТИ.
ТОЧЕЧНАЯ НОРМАЛЬНАЯ ФОРМА ИМЕЕТ ВИД: n ( R C ) 0
n ( R B ) ( 2 , 1 , 2 ) (( x , y , z ) ( 1 ,2 ,3 )) 0
УРАВНЕНИЕ ПЛОСКОСТИ ЗАПИШЕМ СЛЕДУЮЩИМ ОБРАЗОМ:
(2 , 1, 2) (( x, y, z ) (1, 2 , 3)) 0 ;
2 x y 2 z 6 0 ;
2 x y 2 z 6 ;

14.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
ПРИМЕР ПО ИЗВЕСТНОМУ УРАВНЕНИЮ ПЛОСКОСТИ 2x-y+3z=8
ОПРЕДЕЛИТЬ ПАРАМЕТРИЧЕСКУЮ ФОРМУ ОПИСАНИЯ ПЛОСКОСТИ
P ( s, t ) C s a t b
2 x y 3 z 8
( nx , n y , nz )
n (2 , 1, 3)
ЗАДАДИМ ПРОИЗВОЛЬНУЮ ТОЧКУ НА ЗАДАННОЙ ПЛОСКОСТИ C ( 4, 0, 0)
ЗАДАДИМ ДВА ПРОИЗВОЛЬНЫЕ ВЕКТОРА, СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
b (0, 3, 1) (b n 0)
КОТОРЫХ С НОРМАЛЬЮ БУДЕТ РАВНО 0
a (1, 5, 1) (a n 0)
P ( s, t ) (4, 0, 0) (1, 5,1) s (0, 3,1) t

15.

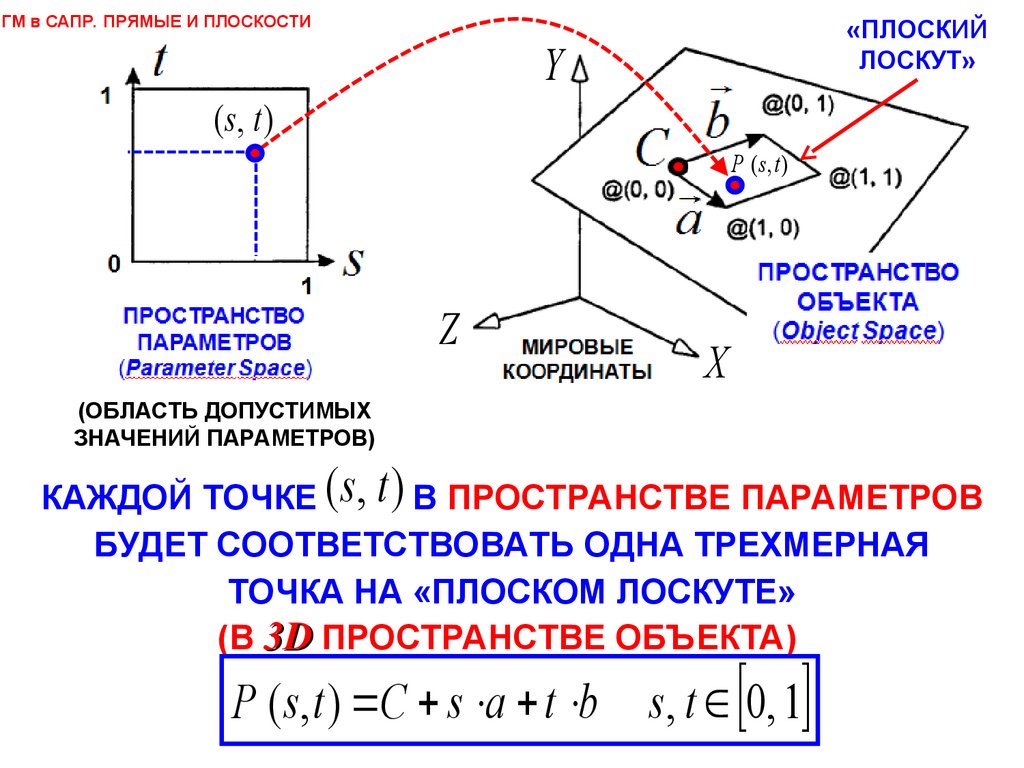
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
ОПИСАНИЕ ФРАГМЕНТОВ ПЛОСКОСТИ
«ПЛОСКИХ ЛОСКУТОВ»
P ( s, t ) C s a t b
s, t s, t
ФРАГМЕНТ ПЛОСКОСТИ НАЗЫВАЕТСЯ
«ПЛОСКИЙ ЛОСКУТ» (Planar Patch)
БОЛЬШАЯ ЧАСТЬ ПРАКТИЧЕСКОГО МОДЕЛИРОВАНИЯ ОБЪЁМНЫХ ТЕЛ
СВОДИТСЯ К СОБИРАНИЮ В ОДНО ЦЕЛОЕ ЛОСКУТОВ РАЗЛИЧНОЙ ФОРМЫ
ДЛЯ СОЗДАНИЯ ПОВЕРХНОСТИ ОБЪЕКТА
«ПЛОСКИЙ ЛОСКУТ»
ЛОСКУТ ФОРМИРУЕТСЯ ПРИ ОГРАНИЧЕНИИ
ДИАПАЗОНА ИЗМЕНЕНИЯ ДОПУСТИМЫХ ЗНАЧЕНИЙ
ПАРАМЕТРОВ s И t.
ЧАСТО БЫВАЕТ УДОБНО, ЧТОБЫ ЗНАЧЕНИЯ s И t ИЗМЕНЯЛИСЬ
ТОЛЬКО В ИНТЕРВАЛЕ ОТ 0 ДО 1
«ПЛОСКИЙ ЛОСКУТ»
ЛОСКУТ ПОЗИЦИОНИРУЕТСЯ И ОРИЕНТИРУЕТСЯ
ВЕКТОРОВ a , b И ТОЧКИ С
В ПРОСТРАНСТВЕ С ПОМОЩЬЮ СООТВЕТСТВУЮЩЕГО ПОДБОРА

16.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
«ПЛОСКИЙ
ЛОСКУТ»
Y
( s, t )
P ( s, t )
Z
X
(ОБЛАСТЬ ДОПУСТИМЫХ
ЗНАЧЕНИЙ ПАРАМЕТРОВ)
КАЖДОЙ ТОЧКЕ ( s, t ) В ПРОСТРАНСТВЕ ПАРАМЕТРОВ
БУДЕТ СООТВЕТСТВОВАТЬ ОДНА ТРЕХМЕРНАЯ
ТОЧКА НА «ПЛОСКОМ ЛОСКУТЕ»
(В 3D ПРОСТРАНСТВЕ ОБЪЕКТА)
P ( s, t ) C s a t b s, t 0, 1

17.

ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
P (0, 0) C ;
РАССМОТРЕННЫЙ «ПЛОСКИЙ ЛОСКУТ»
- ПАРАЛЛЕЛОГРАММ,
ВЕРШИНЫ КОТОРОГО
СООТВЕТСТВУЮТ 4-м ТОЧКАМ P ( s, t )
В ПРОСТРАНСТВЕ ПАРАМЕТРОВ
ОПРЕДЕЛЯЕМЫХ СЛЕДУЮЩИМ
ОБРАЗОМ:
P (1, 0) C b ;
P (0,1) C a ;
P (1,1) C a b
p (1, t ); p (s,1); p (0, t ); p (s, 0) ТРЕХМЕРНЫЕ ПРЯМЫЕ
ВЕКТОРЫ a И b ОПРЕДЕЛЯЮТ
ФОРМУ И ОРИЕНТАЦИЮ ЛОСКУТА
ЕСЛИ ВЕКТОРЫ a И b ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫ,
ТО ЛОСКУТ СТАНОВИТСЯ ПРЯМОУГОЛЬНЫМ
ЕСЛИ, КРОМЕ ТОГО, ОНИ ИМЕЮТ ОДИНАКОВУЮ ДЛИНУ,
ТО ЛОСКУТ СТАНОВИТСЯ КВАДРАТНЫМ
ИЗМЕНЕНИЕ КООРДИНАТ ТОЧКИ С ПРОСТО СДВИГАЕТ ЛОСКУТ
БЕЗ ИЗМЕНЕНИЯ ЕГО ФОРМЫ И ОРИЕНТАЦИИ

18.

ПРИМЕР
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
ТОЧКА C ( 1,3, 2 ) И ДВА ВЕКТОРА
ПУСТЬ
ИЗВЕСТНЫ
a ( 1,1,0 ) и b 1,4 , 2 РАСПОЛОЖЕННЫЕ
НА ОДНОЙ ПЛОСКОСТИ.
ОПРЕДЕЛИТЬ КООРДИНАТЫ ВЕРШИН P ( s ,t )
ФРАГМЕНТА ПЛОСКОСТИ,
ЗАДАННЫЕ ЭТИМИ ЭЛЕМЕНТАМИ
P ( s, t ) C s a t b
P (0, 0) C (1, 3 , 2) ;
P (1, 0) C a (1, 3, 2) (1,1, 0) (2, 4, 2) ;
P (0,1) C b (1, 3, 2) (1, 4, 2) (2, 7, 4) ;
P (1,1) C a b (1, 3, 2) (1,1, 0) (1, 4, 2) (3, 8, 4)

19.

ПРИМЕР
НАЙТИ ЗНАЧЕНИЯ ВЕКТОРОВ a , b И ТОЧКИ C , ОБРАЗУЮЩИХ
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
КВАДРАТНЫЙ ФРАГМЕНТ ПЛОСКОСТИ СО СТОРОНОЙ 4, С ЦЕНТРОМ
НАЧАЛЕ ОТСЧЕТА И ПАРАЛЛЕЛЬНЫЙ ПЛОСКОСТИ XZ
P ( s, t ) C s a t b
C ВЫБИРАЕМ
ЛЮБОЙ УГОЛ, НАПРИМЕР ( 2, 0, 2)
ВЫЧИСЛИМ a и b
В КАЧЕСТВЕ ТОЧКИ
КАЖДЫЙ ИЗ ВЕКТОРОВ ИМЕЕТ
ДЛИНУ 4 И ПАРАЛЛЕЛЕН ОДНОЙ
ИЗ ОСЕЙ X ИЛИ Z
b 0,0,4
Z
2
2, 0, 2
УГЛЫ ФРАГМЕНТА (x, y, z)
( 2 , 0, 2 ) ( 2 , 0, 2 )
( 2 , 0, 2 ) ( 2 , 0, 2 )
b P (0,1) C
P (1,1)
-2
1
-1
0
2, 0, 2
P (0,1)
1
2
P (1, 0)
-1
P (0, 0)
2, 0, 2
-2
2, 0, 2
a P ( 1, 0 ) C
X
C
a 4,0,0

20.

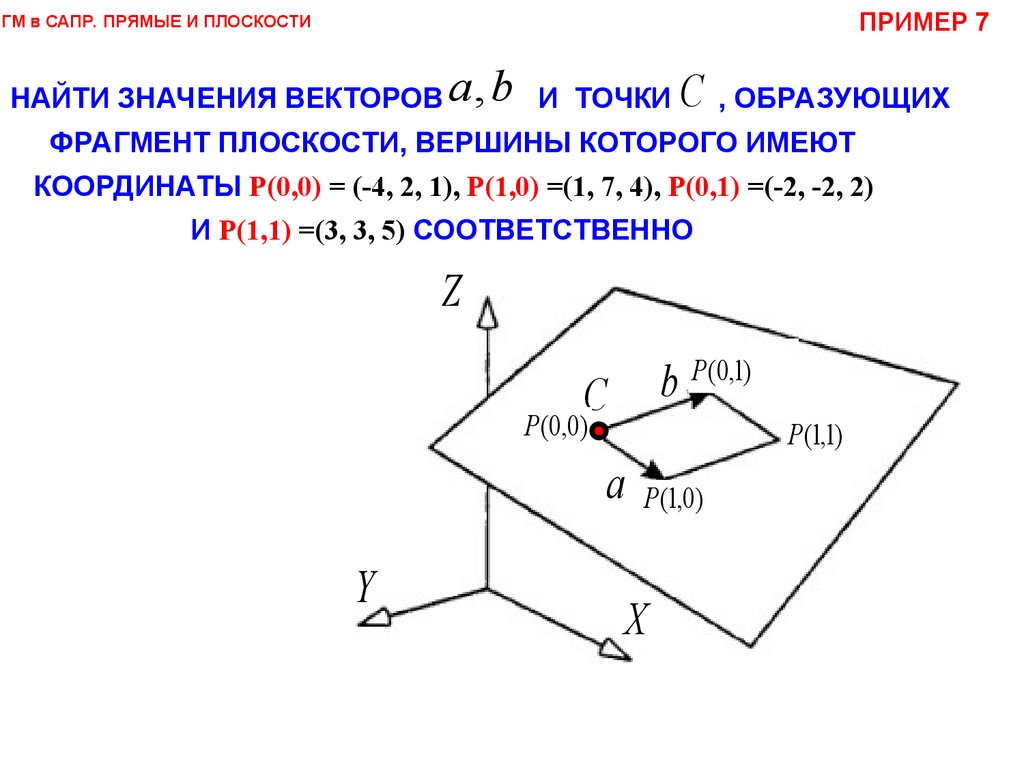
ПРИМЕР 7
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
НАЙТИ ЗНАЧЕНИЯ ВЕКТОРОВ a , b И ТОЧКИ C , ОБРАЗУЮЩИХ
ФРАГМЕНТ ПЛОСКОСТИ, ВЕРШИНЫ КОТОРОГО ИМЕЮТ
КООРДИНАТЫ P(0,0) = (-4, 2, 1), P(1,0) =(1, 7, 4), P(0,1) =(-2, -2, 2)
И P(1,1) =(3, 3, 5) СООТВЕТСТВЕННО
Z
b P(0,1)
C
P(0,0)
Y
a P(1,0)
X
P(1,1)

21.

ПРИМЕР 7
НАЙТИ ЗНАЧЕНИЯ ВЕКТОРОВ a , b И ТОЧКИ C , ОБРАЗУЮЩИХ
ГМ в САПР. ПРЯМЫЕ И ПЛОСКОСТИ
ФРАГМЕНТ ПЛОСКОСТИ, ВЕРШИНЫ КОТОРОГО ИМЕЮТ
КООРДИНАТЫ P(0,0) = (-4, 2, 1), P(1,0) =(1, 7, 4), P(0,1) =(-2, -2, 2)
И P(1,1) =(3, 3, 5) СООТВЕТСТВЕННО
ПРОВЕРИМ
ПУСТЬ
P ( 1, 1 ) C a b
C P ( 0 , 0 ) ( 4 , 2 , 1 )
ВЫЧИСЛИМ ВЕКТОРА
Так как P ( 0 ,1 ) C b то
b P ( 0 ,1 ) C
2 , 2 ,2 4 ,2 ,1 2 , 4 ,1
Так как P ( 1, 0 ) C a то
a P ( 1, 0 ) C
1,7 ,4 4 ,2 ,1 5 ,5 ,3
4 ,2 ,1 5 ,5 ,3 2 , 4 ,1
3,3,5