Similar presentations:
Уравнение прямой и плоскости
1.
GİRİŞ HİSSƏЛЕКЦИЯ 4
УРАВНЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
PLAN
Параметрическое и каноническое уравнение прямой
Общее уравнение прямой
Уравнение прямой в отрезках
Уравнение с угловым коэффициентом
Уравнение прямой, проходящей через две заданные точки
Взаимное расположение двух прямых
Общее уравнение плоскости
Взаимное расположение двух плоскостей
Уравнение прямой в пространстве
Взаимное расположение прямой и плоскости в пространств
2.
ЛИТЕРАТУРА1)
Под ред. Н.Ш.Кремера . Высшая математика для экономистов.
ЮНИТИ 2012
2)
Н.Дж.Мусаев, В.Я.Гюльмамедов. Лекции и задачи по курсу высшей
математики. 1-я и 2-я части, Баку2002
3)
В.А.Ильин . Э.Г.Позняк . Линейная алгебра.-М.: Наука, 2010
4)
В.А.Ильин .Э.Г. Позняк. Основы математического анализа.Часть 1-М.:Физматлит,2005
5)
Д.Т.Письменный. Конспект лекций по высшей математике .Москва.1-я
и 2-я части, 2018
6)
Под ред. В.И.Ермакова. Сборник задач по высшей математике для
экономистов-М.2006
7)
Ю.М.Протасов. Линейная алгебра и аналитическая геометрия .2017
3.
ВВЕДЕНИЕВ этой лекции мы приступим к изучению уравнения прямой и плоскости.
Выясним, какое уравнение может называться уравнением прямой, а какоеуравнением плоскости. Рассмотрим несколько видов уравнения прямой на
плоскости и несколько видов уравнения плоскости в пространстве.
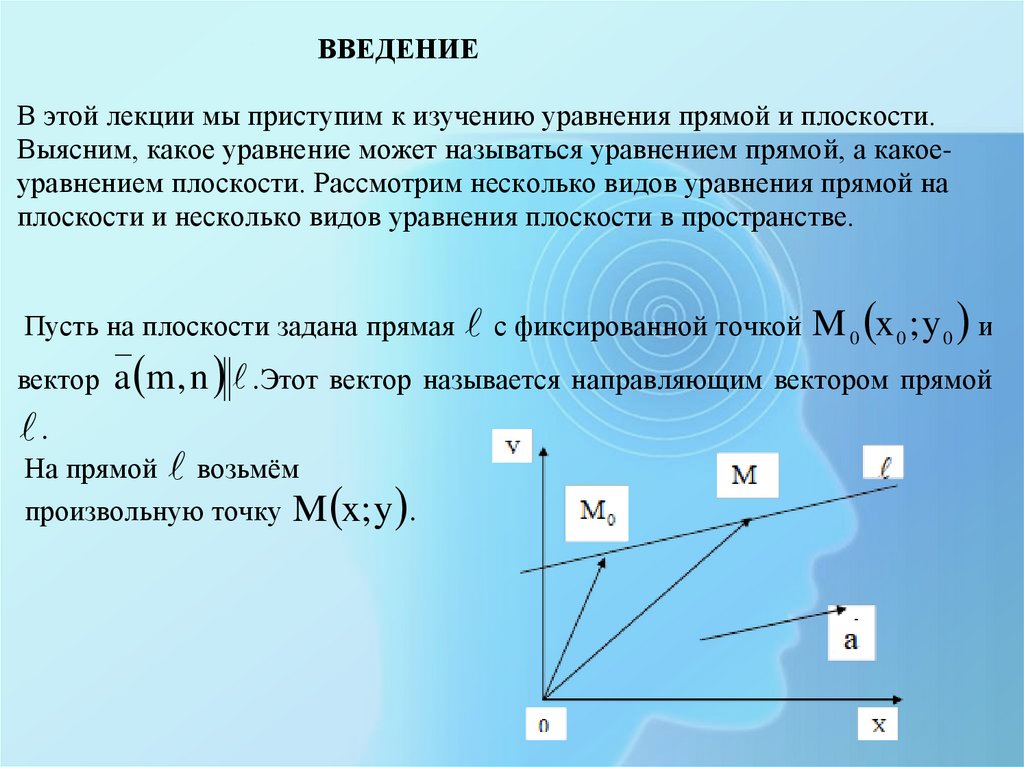
Пусть на плоскости задана прямая с фиксированной точкой M 0 x 0 ; y 0 и
вектор a m , n
.Этот вектор называется направляющим вектором прямой
.
На прямой возьмём
произвольную точку M x; y .
4.
Проведем радиус – векторы:r 0 OM 0 ; r OM .
MM r r 0 коллинеарен
вектору a , поэтому r r 0 t a -векторное уравнение прямой (1).
В координатной форме будет:
x x0 t m
x x 0 ; y y 0 t m ; t n
- параметрическое уравнение. (2)
y y0 t n
Решая систему относительно t получим:
x x0 y y0
- каноническое уравнение прямой.
(3)
m
n
Теперь возьмём вектор N A , B . Этот вектор называется
нормалью прямой .
N N M 0M N , M 0M 0
M 0M r r0 r r 0 , N 0
В координатной форме будет:
A x x 0 A y y 0 B 0
Ax Ax 0 By By 0 0
5.
Ax By Ax 0 By 0 0Ax By C 0 C Ax 0 By 0 - общее уравнение прямой
(4)
Рассмотрим следующие частичные случаи:
1) A 0, B 0, C 0 .
В этом случае уравнение (4) можно
A
C
y x
B
B
y kx b
записать в виде:
Где: k
A
,
B
b
C
B
(5)
k - называется условным коэффициентом и он равен : k tg ,
Где - угол, образованный прямой с положительным направлением оси ОХ;
b - величина отрезка, отсекаемого прямой на оси ОУ, считая от начала
координат.
2) A 0, B 0, C 0 .
Прямая проходит через начало координат.
6.
3) A 0, B 0,C 0
Прямая параллельна оси ОХ.
4) A 0, B 0,
C 0
Прямая параллельна оси ОУ.
5) A 0, B 0,
C 0
Прямая совпадает с осью ОХ.
y 0 - уравнение оси ОХ.
6) A 0, B 0,
C 0
Прямая совпадает с осью ОУ.
x 0 - уравнение оси ОУ.
Пусть прямая проходит через точку A x1 ; y1 и не параллельна оси ОУ.
Запишем уравнение этой прямой:
y y1 k x x1
(5)
Запишем уравнение прямой, проходящей через две данные точки:
A x1 ; y1 , B x 2 ; y 2 .
y y1
x x1
y 2 y1 x 2 x1
(6)
или
x
x1
x2
y
y1
y2
1
1 0
1
(7)
7.
УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ.РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ.
Пусть прямые 1 и 2 заданы их общими уравнениями:
A 1x B1y C1 0
A 2x B2y C 2 0
Угол между этими прямыми определяется как угол между нормалями,
проведенными к этим прямым:
N ,N
Cos
1
2
N1 N 2
A 1A 2 B1B 2
A B
2
1
2
1
A B
2
2
2
2
(8)
Если 0 , то есть прямые параллельны, то:
N1 N 2
A 1 B1
- условие параллельности двух прямых
A 2 B2
(9)
, то есть
Если
прямые
перпендикулярны,
то
2
A 1A 2 B1B2
Cos 0
0 A 1A 2 B1B2 0 - условие
2
2
2
2
2
A 1 B1 A 2 B2
перпендикулярности двух прямых.
(10)
8.
Пусть теперь прямые 1 и 2 заданы уравнениями:y k 1x b 1
y k 2x b 2
Где k 1 tg 1 ;
k 2 tg 2
tg tg 2 1
tg 2 tg 1
k k1
2
1 tg 1 tg 2 1 k 1k 2
(11)
В случае, когда прямые параллельны, 0 ,
тогда tg tg 0 0
k 2 k1
0.
1 k 1k 2
Отсюда получаем k 1 k 2 - условие параллельности двух прямых
В случае, когда прямые
(12).
перпендикулярны, то есть , имеем
2
tg 1 k 1k 2 0
2
- условие перпендикулярности двух прямых (13)
1
k1
k2
9.
Расстояние от точки M x 0 ; y 0 доопределяется по формуле:
d
Ax 0 By 0 C
A B
2
2
прямой
Ax By C 0
(14)
Расстояние между двумя параллельными прямыми, заданными их
A1x B1y C 0; A 2 x B2 y C 2 0 ,
общими
уравнениями
определяется по формуле:
d
C 2 C1
A 2 B2
Примеры.
1) Найти геометрическое место точек равноудаленных от точек A 0;3 и
B 2;0 .
10.
РешениеПусть точка K x; y находится на нужной нам прямой. Тогда по условию
задачи должно выполняться:
AK BK
То есть,
x 0 2 y 3 2 y 2 2 y 0 2
x y 6y 9 x 4x 4 y 4x 6y 5 0
2
2
2
-
2
- уравнение нужной нам прямой.
2). Написать уравнения прямой проходящей через точки A 2;3 и B 3;4 .
Решение
y y1
x x1
y 2 y1 x 2 x1
x 2 y 3
x y 1 0
3 2 4 3
3x y 5 0
3) Найти угол между прямыми: 2x y 1 0,
2 3 1 1
5
1
Cos
4 1 9 1
5 10
2
45o
11.
ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ В ПРОСТРАНСТВЕПусть в пространстве R 3 заданы плоскость с фиксированной точкой
M 0 x 0 , y 0 , z 0 и нормаль N A; B; C .
На плоскости возьмём произвольную
точку M x, y, z . Так как вектор M 0M
Z
лежит на плоскости , то M 0M N
r
0
0
N, r r 0
M
r0
N , M M 0
M 0M r r0
M
M0 0
N
У
Х
0
Запишем это в координатной форме:
A x x 0 B y y 0 C z z 0 0
Ax Ax 0 By By 0 Cz Cz 0 0
(15)
12.
Ax By Cz Ax 0 By 0 Cz 0 0D
Ax By Cz D 0
– уравнение плоскости, проходящей через точку M 0 x 0 , y 0 , z 0
(16) (15)
(16) – общее уравнение плоскости в R 3 .
Уравнение (16) в векторной форме имеет вид:
N, r D 0
Где:
D Ax 0 By 0 Cz 0
Обобщая уравнение (16) для случая
гиперплоскости:
(17)
R n n 3 , получим уравнение
A1x1 A 2 x 2 A n x n D 0
Рассмотрим следующие частные случаи:
1) A 0, B 0, C 0, D 0
Плоскость проходит через начало координат.
2) A 0, B 0, C 0, D 0
By Cz D 0 - уравнение плоскости, параллельной оси ОХ
N 0; B; C OX .
3) A 0, B 0, C 0, D 0
13.
Cz D 0 - уравнение плоскости параллельной плоскости ХОУ. Этаплоскость параллельна осям ОХ и ОУ.
4) A 0, B 0, C 0, D 0
Cz D 0 - уравнение плоскости ХОУ.
Угол между двумя плоскостями:
A1x B1y C1z D 1 0
и
A 21x B2 y C 2 z D 2 0
равен углу между нормалями:
N 1 A 1 ; B1 ; C1 , N 2 A 2 ; B2 ; C 2
N ,N
A A B B C C
Cos Cos N , N
1
1
2
2
N1 N 2
1
2
1
2
1
A B C
Если , то
2
A 1A 2 B1B2 C1C 2 0
условие перпендикулярности двух плоскостей.
2
1
2
2
1
1 2
2 2
2 2
A BC
2
2
(18)
(19)
14.
A 1 B1 C1A 2 B2 C 2
(20)
условие параллельности двух плоскостей.
Если выполняется условие:
A 1 B1 C1 D 1
,
A 2 B2 C 2 D 2
то плоскости совпадают.
Расстояние d от точки M 0 x 0 , y 0 , z 0 до плоскости
Ax By Cz D 0
определяется по формуле:
d
Ax 0 By 0 Cz 0 D
A B C
2
2
2
(21)
15.
УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙЧЕРЕЗ ТРИ ТОЧКИ
Пусть заданы три точки M 1 x1 , y1 , z1 , M 2 x 2 , y 2 , z 2 , M 3 x 3 , y 3 , z 3 , не
лежащие на одной прямой. Для того, чтобы написать уравнения плоскости,
проходящей через эти точки, возьмём на плоскости произвольную точку
M x, y, z . Тогда векторы
M1M x x1, y y1, z z1 , M1M 2 x 2 x1, y 2 y1, z 2 z1 ,
M 1M 3 x 3 x1 , y 3 y1 , z 3 z1 будут лежать на этой плоскости и будут
выполняться равенства:
N , M M 0
N , M M 0
N , M M 0
1
1
2
1
3
Записав эти равенства в координатной форме, получим систему:
A x x1 B y y1 C z z1 0
A x 2 x1 B y 2 y1 C z 2 z1 0
A x 3 x1 B y 3 y1 C z 3 z1 0
16.
Для существования нетривиального решения этой системы необходимо идостаточно, чтобы выполнялось:
x x1
x 2 x1
x 3 x1
y y1
y 2 y1
y 3 y1
z z1
z 2 z1 0
z 3 z1
.
Уравнение плоскости, проходящей через данную точку M 0 x 0 , y 0 , z 0 и
параллельной векторам: a m1 ; n 1 ; p 1 , b m 2 n 2 p 2 имеет вид:
x x0
m1
m2
y y0
n1
n2
z z0
p1 0
p2
(23)
17.
Уравнение плоскости, проходящей через две данные точки M 1 x1 , y1 , z1 ,M 2 x 2 , y 2 , z 2 и параллельной вектору a m, n , p , имеет вид:
x x1 y y1 z z1
x 2 x1 y 2 y1 z 2 z1 0
(24)
m
n
p
Уравнение плоскости, проходящей через точки M 1 x1 , y1 , z1 , M 2 x 2 , y 2 , z 2
и перпендикулярной плоскости Ax By Cz D 0 , имеет вид:
x x1 y y1 z z1
x 2 x1 y 2 y1 z 2 z1 0
(25)
A
B
C
18.
Примеры1) Написать уравнение плоскости, проходящей через точку A 1;3;5 и
имеющей нормаль N 5;3;1 .
Решение
A x x 0 B y y 0 C z z 0 0
5 x 1 3 y 3 1 z 5 0
5x 3y z 5 9 5 0
5x 3y z 19 0
2) Найти угол между плоскостями x 2y 2z 1 0 и x y 4 0
.
19.
CosA 1A 2 B1B 2 C1C 2
A 12 B12 C12
1 2 0
2
2
2
1 4 4 1 1
A 2 B2 C 2
3
1
9 2
2
45o
3) Показать, что данные плоскости
x 2y z 7 0; 2x y z 2 0; x 3y 2z 11 0
Пересекаются в одной единственной точке, и найти координаты этой точки.
20.
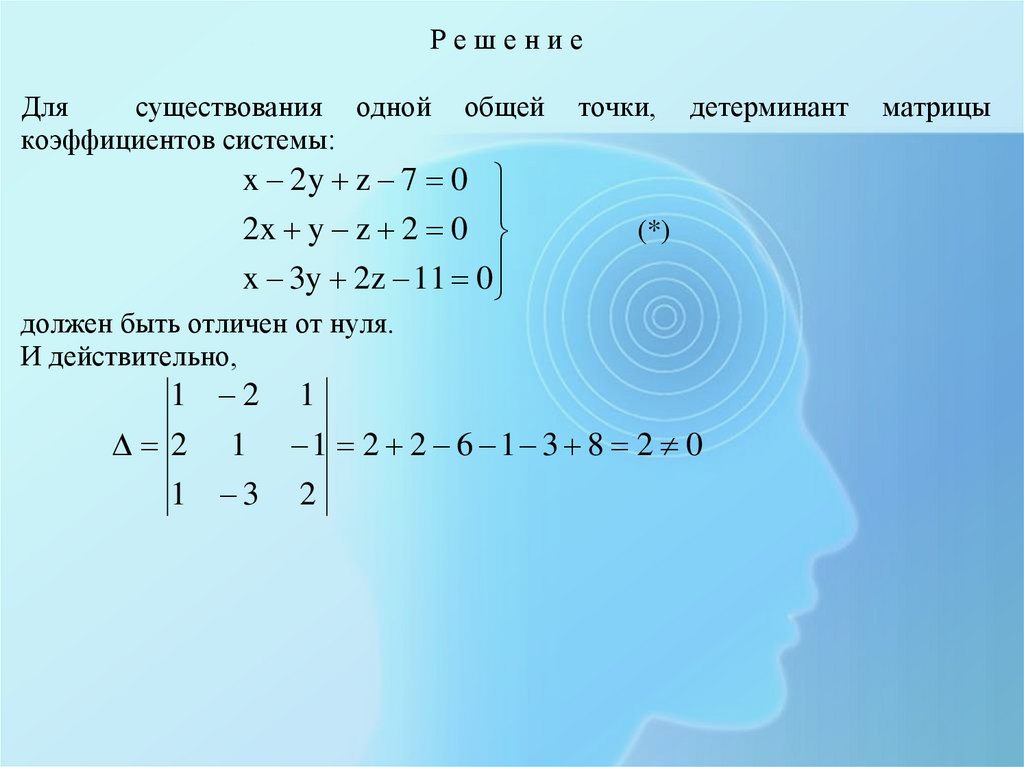
РешениеДля
существования одной
коэффициентов системы:
общей
x 2y z 7 0
2x y z 2 0
x 3y 2z 11 0
точки,
детерминант
(*)
должен быть отличен от нуля.
И действительно,
1 2 1
2 1 1 2 2 6 1 3 8 2 0
1 3 2
матрицы
21.
Для того, чтобы найти координаты точки пересечения заданныхплоскостей, решим систему (*) методом Крамера:
7 2 1
1 2 1 1 14 22 6 11 21 8 2
11 3 2
1 7
1
2 2 2 1 4 7 22 2 28 11 4
1 11 2
1 2 7
3 2 1 2 11 4 42 7 6 44 4
1 3 11
3 4
1 2
2 4
X
1;
2;
Z
2
У
2
2
2
(1; -2; 2) – точка пересечения.
22.
УРАВНЕНИЯ ПРЯМОЙ В ПРОСТРАНСТВЕ.Пусть в R 3 задана прямая , с
фиксированной точкой M 0 x 0 , y 0 , z 0
и задан направляющий вектор
S m, n , p параллельный прямой
На прямой возьмём произвольную
точку M x, y, z .
Так как M 0M лежит на прямой , то
M 0M и S коллинеарны M 0M r r0
r r 0 t s - векторное уравнение
(26)
Запишем это уравнение в координатной форме. Получим:
x x0 t m
y y0 t n
z z 0 t p
- параметрическое уравнение
(27).
23.
Решая эту систему относительно параметра t , получим:x x0 y y0 z z0
- каноническое уравнение
m
n
p
(28)
В пространстве расстояние от точки до прямой определяется по формуле:
d
y1 y 0
n
z1 z 0
z1 z 0
p
p
2
x1 x 0
x1 x 0
m
m
2
m n p
2
2
y1 y 0
n
2
2
(29)
Уравнение прямой, проходящей через точки M 1 x1 , y1 , z1 и M 2 x 2 , y 2 , z 2
имеет вид:
x x1
y y1
z z1
x 2 x1 y 2 y1 z 2 z1
(30)
Угол между прямыми, заданными каноническими уравнениями:
x x1 y y1 z z1
m1
n1
p1
x x2 y y2 z z2
m2
n2
p2
и
24.
Определяется как угол между направляющими векторами этих прямых, тоесть между s1 m 1 ; n 1 ; p 1 и s2 m 2 ; n 2 ; p 2 .
s,s
Cos
1
m 1 m 2 n 1n 2 p 1p 2
2
s1 s2
m n p
2
1
2
1
2
1
m n p
2
2
2
2
(31)
2
2
m1 n 1 p1
- условие параллельности.
m2 n2 p2
m1m 2 n 1n 2 p1p 2 0 - условие перпендикулярности.
Пусть прямая в R 3 задана каноническим уравнением
x x0 y y0 z z0
,
m
n
p
а плоскость – общим уравнением
Ax By Cz D 0
25.
Угол между этими прямой и плоскостью определяется как угол междунаправляющим вектором s m ; n ; p прямой и нормалью N A ; B; C
плоскости:
Sin
A m Bn C p
A B C
2
Если 0 , то Sin 0
2
2
(32)
m n p
A m Bn C p
2
2
2
A B C m n p
2
2
2
2
2
2
0
A m Bn C p 0 - условие параллельности прямой и плоскости.
A m Bn C p
1
Если , то Sin
2
2
2
2
2
2
2
2
A B C m n p
A B C
- условие перпендикулярности прямой и плоскости.
m n p
26.
Примеры1) Написать каноническое уравнение прямой, проходящей через точку
A 2;0; 3 и имеющей направляющий вектор s 2; 3;5
Решение
x x0 y y0 z z0
m
n
p
x 2
y z 3
2
3
5
x 3 y 1 z 3
2) Найти угол между прямой
и плоскостью
2
3
2
x 2y 2z 6 0 .
Решение
sin
2 6 4
0 0 параллельны.
1 4 4 4 9 4
Условия параллельности также выполняется:
A m Bn C p 2 6 4 0
3). Найти точку пересечения прямой:
x 3 y 1 z 3
и плоскости x 2y 2z 6 0 .
2
3
2
27.
РешениеНапишем параметрическое уравнение прямой:
x 2t 3
x 3 y 1 z 3
t y 3t 1
2
3
2
z 2t 3
Учитывая эти равенства в уравнении плоскости, получим:
2t 3 2 3t 1 2 2t 3 6 0
2t 3 6t 2 4t 6 6 0
1 0
Данные прямая и плоскость не пересекаются они параллельны.
4) Доказать параллельность прямых
2x 2y z 10 0
,
x y z 22 0
x 7 y 5 z 9
3
1
4
28.
РешениеДанная система содержит уравнения двух плоскостей, пересечением
которых является данная прямая. Приведем уравнение прямой к
каноническому виду.
2x 2y z 10 0
x 12 y
x 3y 12 0
3
1
x y z 22 0
2x 2y z 10 0
z 34 y
4
y
z
34
0
4
1
x y z 22 0
И так, получим:
x 12 y z 34
3
1
4
Выполняется условие параллельности двух прямых:
m1 n 1 p1
m2 n2 p2
3 1 4
3 1 4
29.
ИТОГИтак, в этой лекции мы рассмотрели несколько видов уравнения прямой на
плоскости , несколько видов уравнения плоскости в пространстве, а также
уравнение прямой в пространстве. Определили взаимное расположение двух
прямых на плоскости, двух плоскостей в пространстве и взаимное
расположение прямой и плоскости в пространстве.
30.
КОНТРОЛЬНЫЕ ВОПРОСЫКакое уравнение называется общим уравнением прямой на
1)
плоскости
2)
Какое уравнение называется параметрическим,а какоеканоническим уравнением прямой
3)
Написать уравнение прямой, проходящей через две заданные
точки
4)
Как определяется угол между двумя прямыми на плоскости
5)
Условие параллельности и перпендикулярности двух прямых
6)
Общее уравнение плоскости
7)
Взаимное расположение двух плоскостей
8)
Уравнение прямой в пространстве
9)
Взаимное расположение прямой и плоскости в пространстве




























 mathematics
mathematics








