Непрерывность функции

1. Непрерывность функции

Метод интервалов

2. Непрерывность функции

• Если lim f x f x0 то функцию f (x)
x x0
называют непрерывной в точке х0.
• Если функция непрерывна в каждой точке
некоторого промежутка, то ее называют
непрерывной на этом промежутке. (сам
промежуток называют промежутком
непрерывности функции)
• График функции на этом промежутке
представляет собой непрерывную линию, о
которой говорят, что ее можно «нарисовать, не
отрывая карандаша от бумаги».

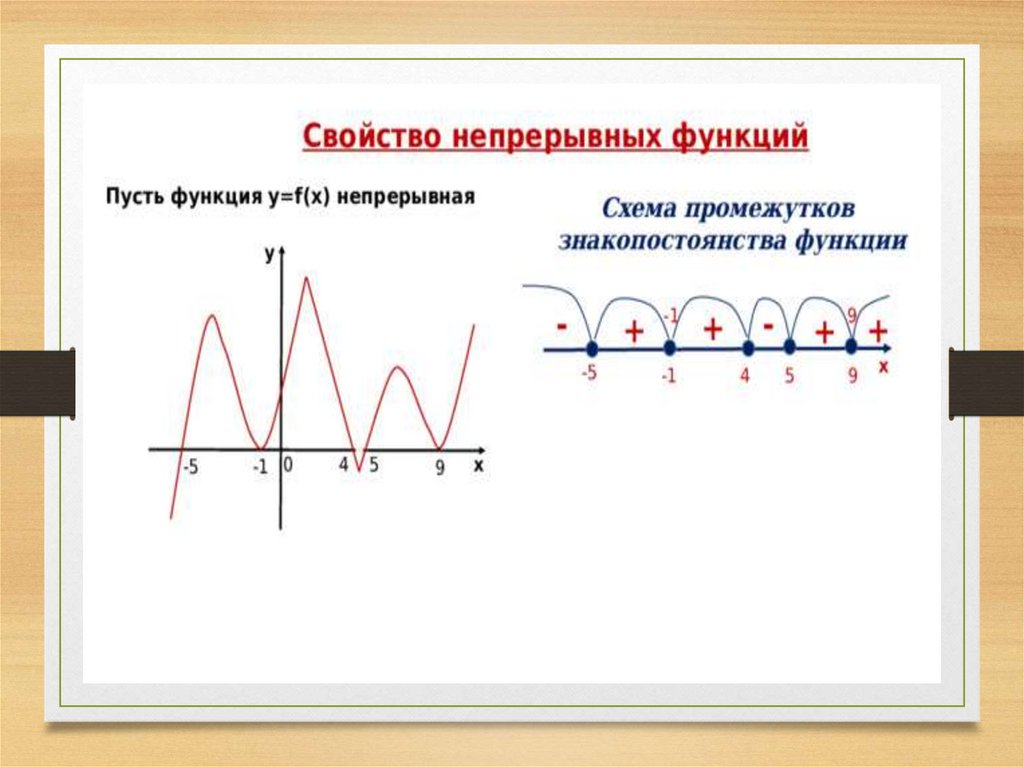
3. Главное свойство непрерывных функций

• Если на интервале (a ; b) функция
непрерывна и не обращается в ноль,
то она на этом интервале сохраняет
постоянный знак.
• На этом свойстве основан метод
решения неравенств с одной
переменной – метод интервалов.

4.

5.

6.

7.

8.

9. Связь между непрерывностью и дифференцируемостью функции

Теорема
Если функция f(x) дифференцируема в некоторой
точке, то она непрерывна в ней.
!!! Обратное утверждение не верно: непрерывная
функция может не иметь производной.

10. Метод интервалов

Пусть функция непрерывна и обращается в ноль
в конечном числе точек. По свойству
непрерывных функций этими точками ОДЗ
разбивается на интервалы, в каждом из которых
непрерывная функция сохраняет постоянный
знак.
+
+
+
a
-
b
c
-
d
x

11.

Алгоритм решения неравенств
методом интервалов
Если неравенство имеет вид f(x)<0 (а также f(x) > 0 или f(x) ≤ 0 или
f(x) ≥0), то его удобно решать методом интервалов.
1. Сначала находят нули каждого множителя, а если в левой части
неравенства – дробь, то находят нули числителя и нули знаменателя.
(Нули числителя и знаменателя – это значения переменной, при
которых числитель и знаменатель становятся равными нулю). Для
этого каждый множитель левой части (числитель и
знаменатель) приравнивают к нулю, и решают полученные
уравнения.
*Примечание. Важно понимать, что нулями каждого множителя
левой части (нулями числителя и знаменателя) могут быть любые
числа, среди которых может отсутствовать число 0.

12.

2. На числовую прямую наносят точки, соответствующие найденным в
пункте 1) нулям. (Не обязательно соблюдать единичные отрезки,
достаточно придерживаться известного правила: точка с меньшей
координатой находится левее точки с большей координатой). После этого
определяют, как их надо изобразить: темными или светлыми (выколотыми).
При решении строгого неравенства (со знаком < или >) все точки
изображаются светлыми (выколотыми). При решении нестрогого
неравенства (со знаком ≤ или ≥) точки, отвечающие нулям знаменателя,
изображаются вколотыми. Все отмеченные точки разбивают координатную
прямую на несколько числовых промежутков.
3. Определяют знаки выражения f(x) из левой части решаемого неравенства на
каждом промежутке и над ними проставляются + или − в соответствии с
определенными знаками.
4. Наконец, при решении неравенства со знаком < или ≤ штриховку наносят
над промежутками, отмеченными знаком «− », а при решении неравенства со
знаком > или ≥ – над промежутками, отмеченными знаком «+». В результате
получается геометрическое представление числового множества, которое и
является искомым решением неравенства.

13.

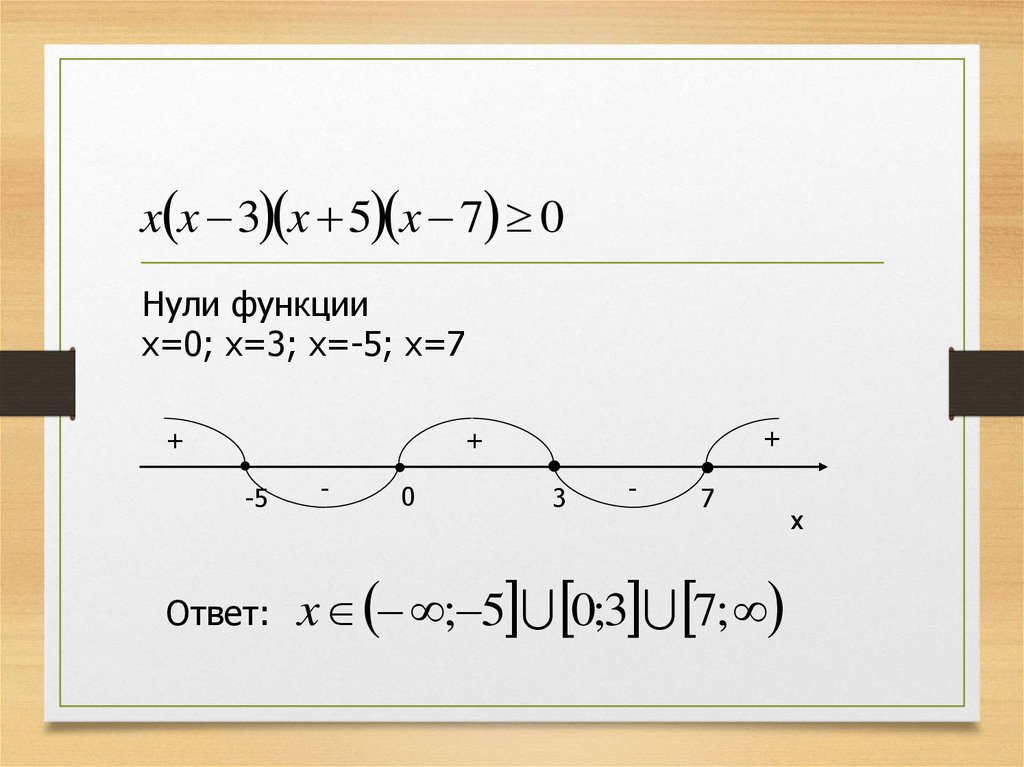
x x 3 x 5 x 7 0
Нули функции
x=0; x=3; x=-5; x=7
+
+
+
-5
Ответ:
-
0
3
-
7
x ; 5 0;3 7;
x

14.

x 3 x 5 0
x 2 x 1
Нули функции
x=3; x=-5
Функция не существует
x=-2; x=1
+
+
-5
-
-2
+
1
Ответ: x 5; 2 1;3
-
3
x

15.

x 4 x 5 0
x 2 x 7
Нули функции
x=4; x=-5
Функция не существует
x=-2; x=-7
+
+
-7
Ответ:
-
-5
+
-2
-
4
x
x ; 7 5; 2 4;

16.

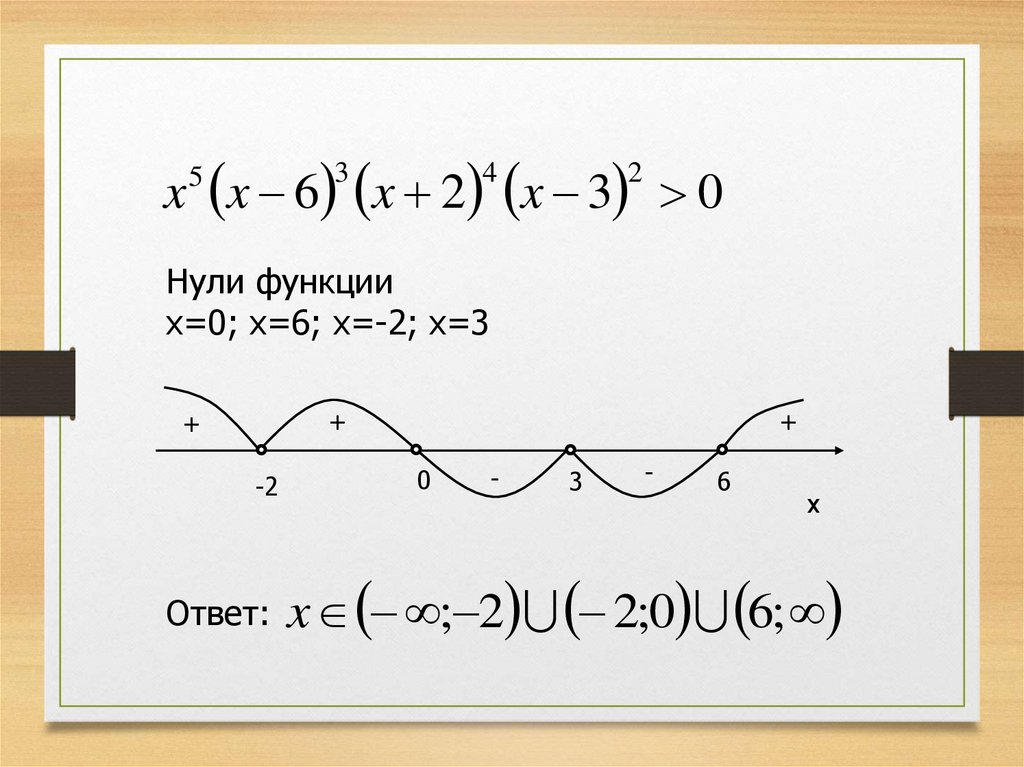
x x 6 x 2 x 3 0
3
5
4
2
Нули функции
x=0; x=6; x=-2; x=3
+
+
+
0
-2
-
3
-
6
x
Ответ: x ; 2 2;0 6;

17.

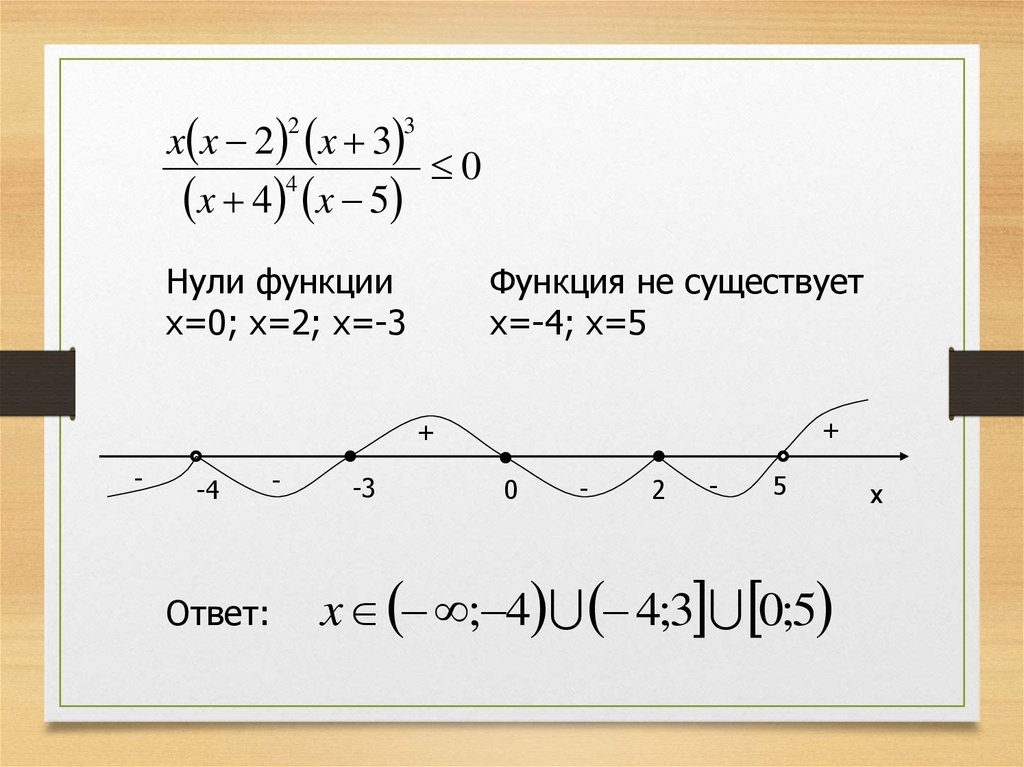
x x 2 x 3
0
4
x 4 x 5
2
3
Нули функции
x=0; x=2; x=-3
Функция не существует
x=-4; x=5
+
+
-
-4
Ответ:
-
-3
0
-
2
-
5
x ; 4 4;3 0;5
x