Similar presentations:
Алгебраические уравнения и неравенства
1. Тема 1. Алгебраические уравнения и неравенства.
Решение уравнений1 и 2 степени.
2. Уравнения с одной переменной
Определениеf ( x) g ( x)
Равенство с переменной
называется уравнением с одной
переменной.
Корень уравнения Значение переменной, при котором
уравнение обращается в верное
равенство.
3.
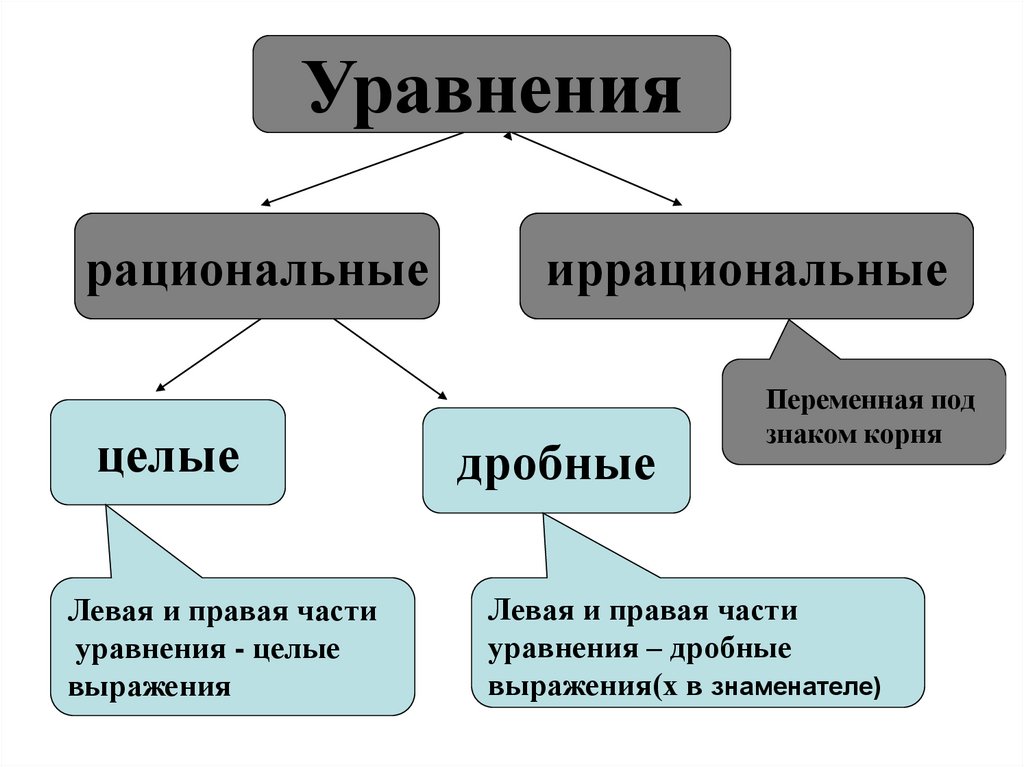
Уравнениярациональные
целые
Левая и правая части
уравнения - целые
выражения
иррациональные
дробные
Переменная под
знаком корня
Левая и правая части
уравнения – дробные
выражения(х в знаменателе)
4. Целые уравнения
Линейные уравнения и уравнения,приводимые к виду
ax b
Квадратные уравнения и уравнения,
приводимые к виду
ax bx c 0
2
5.
Линейным уравнением с одной переменнойназывается уравнение вида
ax b ,
где
x - переменная, a и b – числа.
Решение линейного уравнения
b
Если a 0, то x - единственный корень.
a
Если
, то корней нет.
Если a 0 и
, то корнем является
любое число.
a 0
b 0
6. Приведение уравнения к виду
ax b1.Раскрытие скобок
2.Перенос слагаемых с
противоположным знаком
3.Приведение подобных слагаемых
4.Приведение к общему знаменателю
7. Пример
1. 5 x 20 4 x 1505 x 100 4 x 150;
5 x 4 x 150 100;
x 50.
Ответ: 50
2. Решить самостоятельно:
7 x 0,5 6 1,5 2x 1
Ответ: 0,5
8.
3. x 2 2 x3
5
15
x 2 5 2 15 x 3
5 x 10 30 3 x
5 x 3x 10 30
2 x 40
x 40 : 2
x 20
Ответ: 20
ОЗ 3;5 15
9.
4. Решить самостоятельно:x 1 2x 5x
2
3
6
Ответ: 1,5
10.
Квадратным уравнением называется уравнениевида
ax bx c 0
2
,
где коэффициенты a, b, c – любые действительные числа,
причем
Полное, если b и с отличны от нуля
Неполное , если b или с равны нулю
x2+4x=0
-5x2+45=0
4x2=0
11.
Решение полных квадратных уравненийax2+bx+c=0
D=b2-4ac
Если b=2k, то
•если D<0, то
корней нет
•если D=0, то один
корень
D1=k2-ac
b
x
2a
•Если D>0, то два
корня:
b D
x1
2a
x2
b D
2a
k D1
x1
a
x2
k D1
a
Теорема Виета
(обратная)
Свойства
1) если
a+b+c=0, то
x1 x 2
x1 x 2
c
a
b
a
x1=1, x2=c/a
2) если
a-b+c=0, то
x1=-1, x2=-c/a
12. Пример
5. 2 x 2 7 x 4 0.D 7 2 4 2 ( 4) 49 32 81
D 0,2корня
7 81 7 9 1
x1
2 2
4
2
7 9
x2
4
4
Ответ: 0,5 и -4
13.
№6.x 5x 6 0
2
x1 x2 6
x1 x2 5
x1 2, x2 3
№ 7. 2 x 3 x 5 0
2 3 5 0
5
x1 1, x2 2,5
2
2
№8. 3 x 4 x 1 0
3 4 1 0
1
x1 1, x2
3
2
14. Решить самостоятельно:
№9.№10.
6х х 1 0
2
2х 9х 4 0
2
№11.
х 7 х 10 0
№12.
2х 5х 3 0
№13.
2
2
5 х 3х 8 0
2
Ответы:
№9. 1/3 и -0,5
№10. 4 и 0,5
№11. 2 и 5
№12. 1 и 1,5
№13. -1 и 1,6
15.
Решение неполных квадратных уравнений:вид
ax2=0
ax2+c=0
ax2+bx=0
решение
x=0
ax 2 c 0;
ax 2 bx 0;
x ax b 0;
x 0 или ax b 0
ax b
b
x
a
ax 2 c;
c
x2
a
c
Если.
0,
a
c
x1, 2
a
c
Если
0, то
a
корней нет
16. Пример
45 0 №15. x 8 x 0;x x 8 0
2
5 x 45
x 0 или x 8 0
№14. 5 x
2
2
x 45 : 5
2
x 8
x 9
2
x 3
Ответ: 3 и -3
Ответ: 0 и 8
17. Решить самостоятельно
№16.5 x 20 x 0
№17.
2 x 32 0
№18.
4 x 16 0
2
2
Ответ:
№16. 0 и -4
№17. 4 и -4
№18. нет корней
2
18. Домашнее задание
Принести тонкуютетрадь для
проверочных работ.
2. Скачать с
server1/general/матем
атика
Методичку по теме
«Уравнения и
неравенства».
3. Решить уравнения:
1.
1,2 x 2 2 x 4 1,2 x
x 3 x 2
3
6
8
2
2 x 3x 5 0
6 x 12 x 0
2
3 x 75 0
2
19. Ответы:
51. 1
11
3
2. 9
7
3. -1 и 2,5
4. 0 и -2
5. 5 и -5






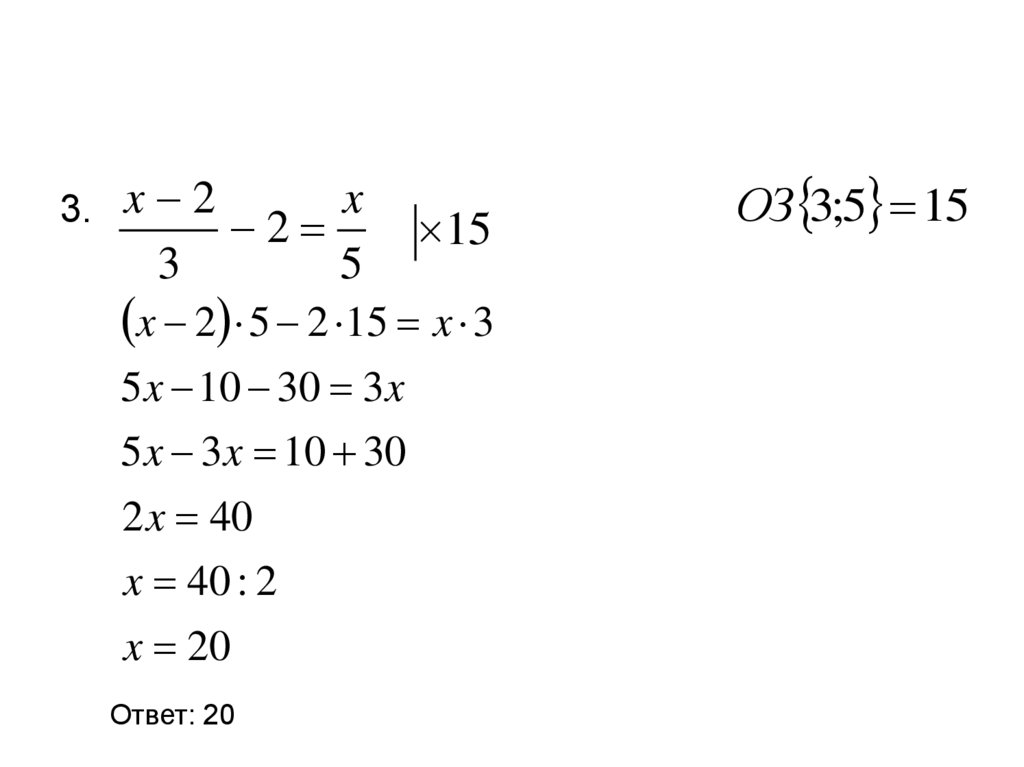




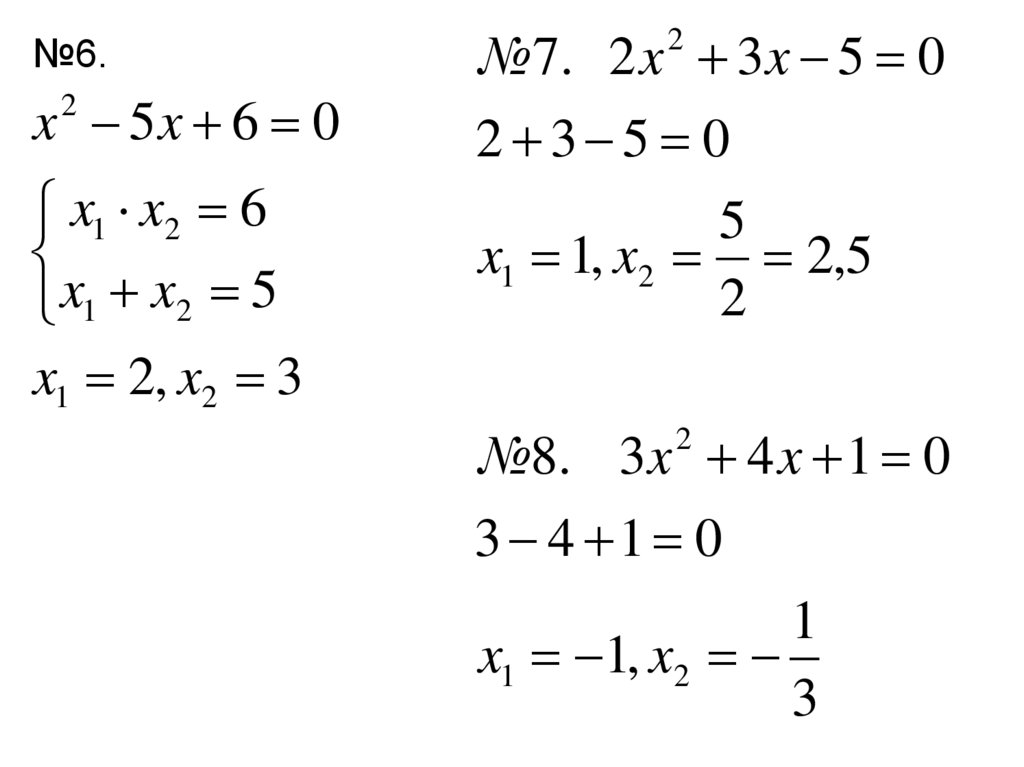






 mathematics
mathematics