Similar presentations:
Квадратные уравнения. Основные понятия
1. КВАДРАТНЫЕ УРАВНЕНИЯ. ОСНОВНЫЕ ПОНЯТИЯ
2.
Квадратным уравнением называютуравнение вида ax2+bx+c=0, где коэффициенты a, b, c –
любые действительные числа, причем a=0
.
Определение
1:
Многочлен ax2+bx+c называют квадратным
трехчленом
а – первый (старший) коэффициент
b – второй коэффициент (коэффициент при х)
с – свободный член
Квадратное уравнение называют
приведенным, если старший коэффициент равен 1;
квадратное уравнение называют непривиденным, если
старший коэффициент отличен от 1.
Определение
2:
3.
2x2 x 3 0- неприведенное квадратное уравнение.
x 2 3x 4 0
- приведенное квадратное уравнение.
Полное квадратное уравнение – это
квадратное уравнение, в котором присутствуют все три
слагаемых; это уравнение, у которого коэффициенты
b, c отличны от нуля.
Определение 3:
Неполное квадратное уравнение – это квадратное
уравнение, в котором присутствуют не все три
слагаемых; это уравнение, у которого хотя бы один из
коэффициентов b, c равен нулю.
4.
Определение4:
Корнем
квадратного
уравнения
ax2+bx+c=0 называют всякое значение переменной х,
при
котором
квадратный
трехчлен
ax2+bx+c
обращается в нуль; такое значение переменной х
называют корнем квадратного трехчлена
Корень квадратного уравнения ax2+bx+c=0 - это такое
значение переменной х, подстановка которого в уравнение
обращает уравнение в верное числовое равенство 0=0
Решить квадратное уравнение – значит найти все его
корни или установить, что корней нет
5.
Пример 1: Решить неполное квадратное уравнениеЕсли произведение равно нулю, то среди множителей есть хотя бы одно
2
число, которое равно нулю. То есть, вне зависимости от
a) 2 x 7 x 0;
количества множителей, если одно из
x(2 x 7) 0;
x 0;
2 x 7 0;
x 3,5.
б ) x 2 5 x 0;
x( x 5) 0;
в) x 2 16 0;
( x 4)( x 4) 0
г ) 2 x 2 7 0;
x 2 3,5;
д) 3x 2 10 0;
3x 2 10;
е) 5x 2 0;
x 2 0;
них равно 0, произведение всегда равно нулю. Это
главное свойство такого произведения.
x1 0, x2 3,5.
x1 0, x2 5.
x1 4, x2 4.
x1, 2 4.
x1 3,5, x2 3,5.
x1, 2 3,5.
нет действтельных корней
x 0.
6.
ОпределениеПолным квадратным уравнением называется
Числа а, в, с – это
коэффициенты квадратного уравнения
а – первый или старший коэффициент;
в – второй коэффициент;
с – свободный член
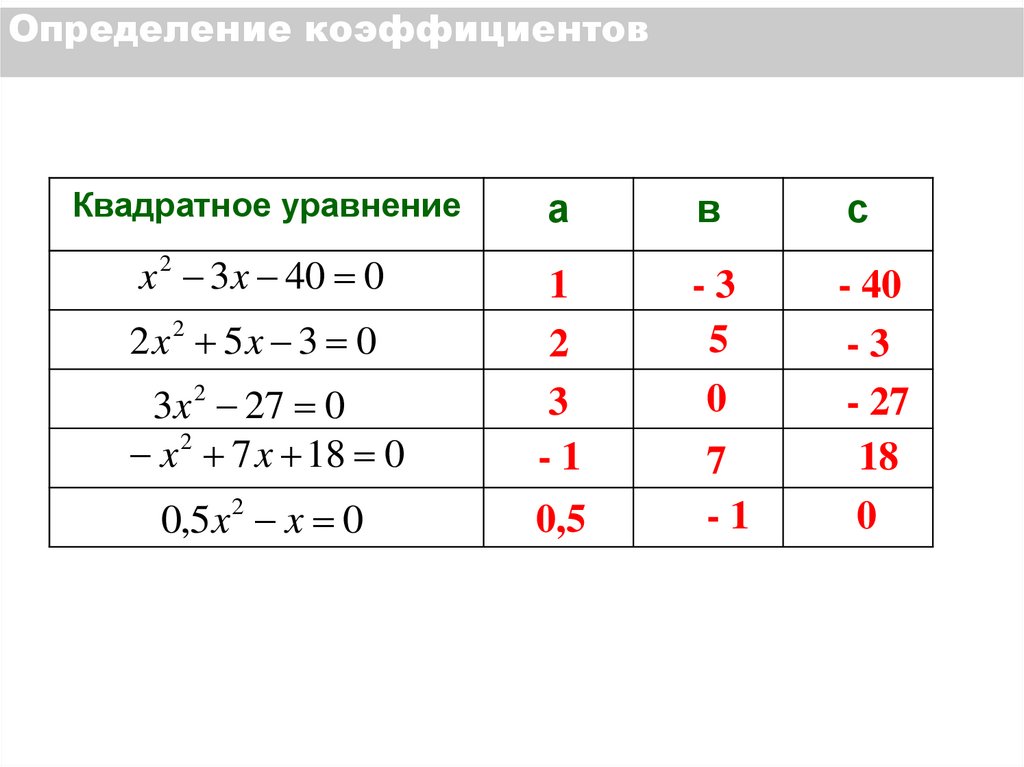
7. Определение коэффициентов
Квадратное уравнениеа
в
с
3x 2 27 0
2
x 7 x 18 0
1
2
3
-1
-3
5
0
0,5x 2 x 0
0,5
- 40
-3
- 27
18
0
x 2 3x 40 0
2 x 2 5x 3 0
7
-1
8.
Решение квадратного уравнения по формулеАлгоритм решения квадратного уравнения вида
ax bx c 0
2
, где
1. Находят дискриминант
2. Если
D 0
, то
3. Если
D 0 , то
4. Если
D 0
x1, 2
a 0
по формуле
D b 4ac
2
b D
2a
b
x1 х2
2a
, то (корней нет)
(2 корня)
(1 корень)
9.
Пример: Решить уравнение 3х2+8х-11=0.Решение:
a 3, b 8, c 11,
D b 2 4ac 82 4 3 ( 11) 64 132 196;
D 0:
b D 8 196 8 14
1;
x1
6
2a
2 3
11
2
b D 8 196 8 14
3 .
x2
6
3
3
2a
2 3
1;
2
3 .
3
10.
Примеры: Решить уравнение: a) x 2 3x 5 0;Решение:
a) x 2 3x 5 0;
a 1, b 3, c 5,
б ) 9 x 2 6 x 1 0;
в) 2 x 2 x 3,5 0;
D b 2 4ac 32 4 1 ( 5) 9 20 29;
D 0:
b D
3 29
b D
3 29
; x2
x1
.
2
2a
2a
2
б ) 9 x 2 6 x 1 0;
9 x 2 6 x 1 (3x 1)2 ;
9 x2 6 x 1 0;
(3x 1)2 0;
a 9, b 6, c 1,
3 x 1 0;
D b 2 4ac 36 36 0;
b
6
1
x
.
2a 2 9 3
1
x .
3
11.
Пример: Решить уравнение:в) 2 x 2 x 3,5 0;
a 2, b 1, c 3,5,
D b 2 4ac 12 4 2 3,5 1 28 27;
D 0:
Уравнение корней не имеет
12.
b b2 4acx1,2
2a
D b 2 4ac 0
D b 4ac 0
2
D b 2 4ac 0
-
КОРНЕЙ НЕТ
b 0
b
x1,2
2a
2a
-
-
ОДИН КОРЕНЬ
ДВА КОРНЯ
b b2 4ac
x1
,
2a
b b2 4ac
x2
2a
13. Решение квадратного уравнения по свойству коэффициентов:
Если в квадратном уравнении ax bx c 0с
a b c 0 , то х1 1, х2 а
2
1
– 2013 : 3 = – 671
14. Решение по формуле
Решение:а = 3, в = 2010, с = - 2013
D b 2 4ac
x1, 2
b D
2a
Ответ:
15. Решение квадратного уравнения по свойству коэффициентов:
Если в квадратном уравнении ax bx c 0с
a b c 0 , то х1 1, х2 а
2
Решите устно квадратные уравнения, используя
свойство коэффициентов:















 mathematics
mathematics








