Similar presentations:
Квадратные уравнения
1. Квадратные уравнения
2.
Цели:1.Систематизация знаний по теме
«Квадратные уравнения»;
2.Развитие интереса к предмету.
Задачи:
1.Знать определение квадратного
уравнения, типы, методы решения;
2.Понимать отличительные
особенности квадратных уравнений;
3.Применять полученные знания при
решении рациональных, иррациональных
уравнений, сокращении дробей, решении задач.
3.
Квадратныеуравнения
умели решать
около 2000 лет
до н. э.
вавилоняне.
4.
ДИОФАНТ В арифметике Диофанта
отсутствуют понятие
отрицательного числа и общие
методы решения квадратных
уравнений.
325 – 409 г.г. по Р. Х.
знаменитый
александрийский
математик.
При составлении уравнений
Диофант для упрощения
решения умело выбирает
неизвестные.
5. Задача Диофанта
Найти два числа, зная, что их сумма равна 20, апроизведение — 96.
Предположим, что искомые числа равны:
ПРОТИВОРЕЧИЕ
С
УСЛОВИЕМ!!!
6.
Если эти числа не равны, тогдаодно из этих чисел будет больше половины их суммы,
т. е. (10 + х),
другое же меньше, т. е. (10 – х).
Разность между ними 2х.
Отсюда уравнение:
(10+x)(10—x) =96,
100 —x2 = 96.
x2 - 4 = 0
х=2
Одно из искомых чисел равно 12, другое 8.
Решение х = - 2 для Диофанта не существует, так как
греческая математика знала только положительные
числа.
7.
Интересные способы решенияквадратных уравнений
встречаются в трудах индийского
ученого Бхаскары
(600 – около 680г.г.).
И арабского ученого
Ал – Хорезми
(780 – около 850г.г.)
8. Задача знаменитого индийского математика XII в. Бхаскары:
Определение квадратногоуравнения
Квадратным уравнением
называется уравнение вида
ax bx c 0,
2
где коэффициенты a,b,c-любые
действительные числа, причем
a 0.
9.
Определение корня• Корнем квадратного уравнения
ax bx c 0
2
называют такое значение переменной х,
при котором квадратный трехчлен
2
ax bx c обращается в нуль;
10.
Типы квадратныхуравнений
• полные
b 0, c 0
• неполные
а) b 0
б) c 0
в) b 0; c 0
11.
Данные уравнения разбейте наполные и неполные:
a)9х2=0;
б)3x+ x2+1=0;
в)2x2-32=0;
г) x2+4x=0;
д)2х2+5х-7=0;
е)12-х2+3х=0.
12. Определение корня
полные:б) 3х+х2+1=0;
д)2х2+5х-7=0;
неполные:
а) 9х2= 0;
в) 2х2-32=0;
г) х2+4х=0.
е)12-х2+3х=0.
13. Типы квадратных уравнений
Способы решения неполныхквадратных уравнений
b=0
ax 2 c 0
c
2
x
a
с
если 0, то
а
c
x1, 2
a
c=0
ax 2 bx 0
x (ax b) 0
b
x 0 или x
a
b=0;c=0
ax 0
2
x 0
x 0
2
14.
Решите уравнения:x1 3; x2 3
a) x 9;
2
б )10 x x 0;
x1 0; x2 10
в )2 x 8 0;
x1 2; x2 2
г )3x 27 0.
корней
нет
2
2
2
15.
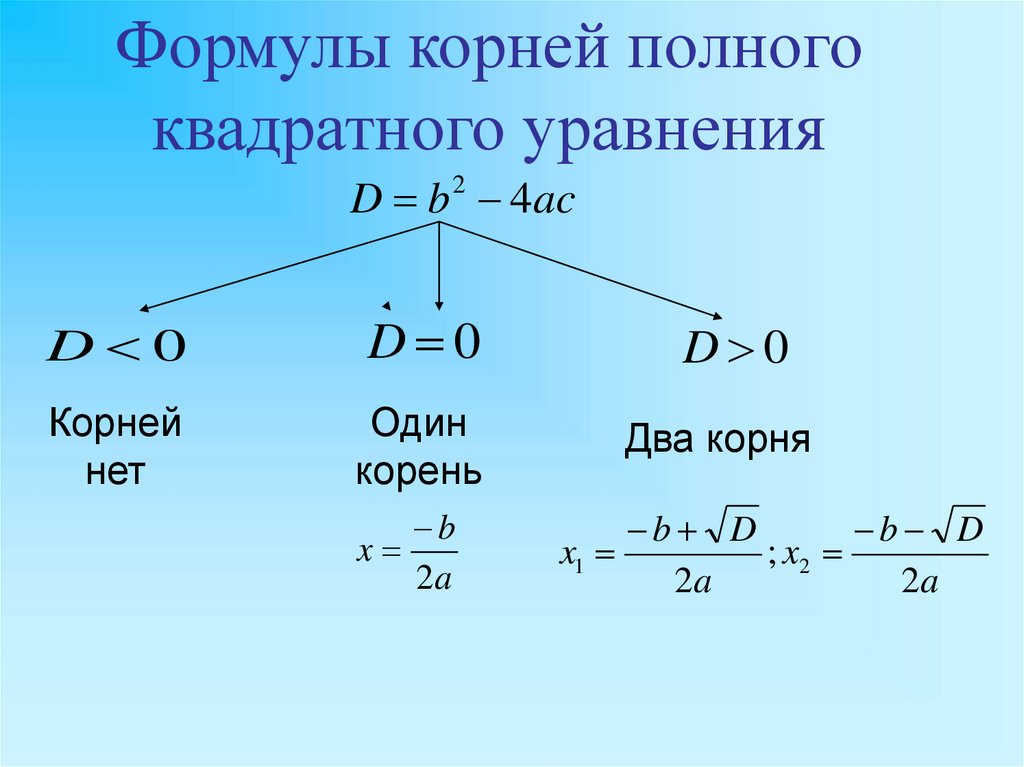
Формулы корней полногоквадратного уравнения
D b 2 4ac
D 0
D 0
D 0
Корней
нет
Один
корень
Два корня
b
x
2a
b D
b D
x1
; x2
2a
2a
16. Способы решения неполных квадратных уравнений
Формула четногокоэффициента
b=2k
k k ac
x1, 2
a
a=1
2
x1, 2 k k c
2
17. Решите уравнения:
Теорема Виетаx1 , x2 - корни квадратного уравнения
b
x1 x2
a
c
x1 x2
a
a 1
x1 x2 b; x1 x2 c
18. Формулы корней полного квадратного уравнения
1.Найдите корни квадратного уравнения,не используя формулы корней:
а ) x 2 5 x 6 0;
x1 2; x2 3
б ) x 3 x 4 0;
x1 4; x2 1
в ) x 2 5 x 10 0.
Корней нет
2
2.Составьте приведенное квадратное
уравнение, корнями которого являются
числа 3 и -7:
x 2 4 x 21 0
19. Формула четного коэффициента
Применение квадратныхуравнений
-решение рациональных уравнений;
-решение иррациональных уравнений;
-решение задач;
-разложение квадратного трехчлена на
множители;
-сокращение дробей.


















 mathematics
mathematics