а 8

1.

17.11.2024
.

2.

Укажите допустимые значения
переменной в выражении:
2
5
а) ; х ≠ 0; б) у у ;у ≠ 3;
х
у 3
7
в) 2
; х – любое число;
х 4
2
х 9
г)
; х – любое число;
3
1
д) 19х
; х ≠ 2;
6х 12
13 х
е)
; х ≠ 0; х ≠ – 2;
х(х 2)

3.

17.11.2024
Классная работа

4.

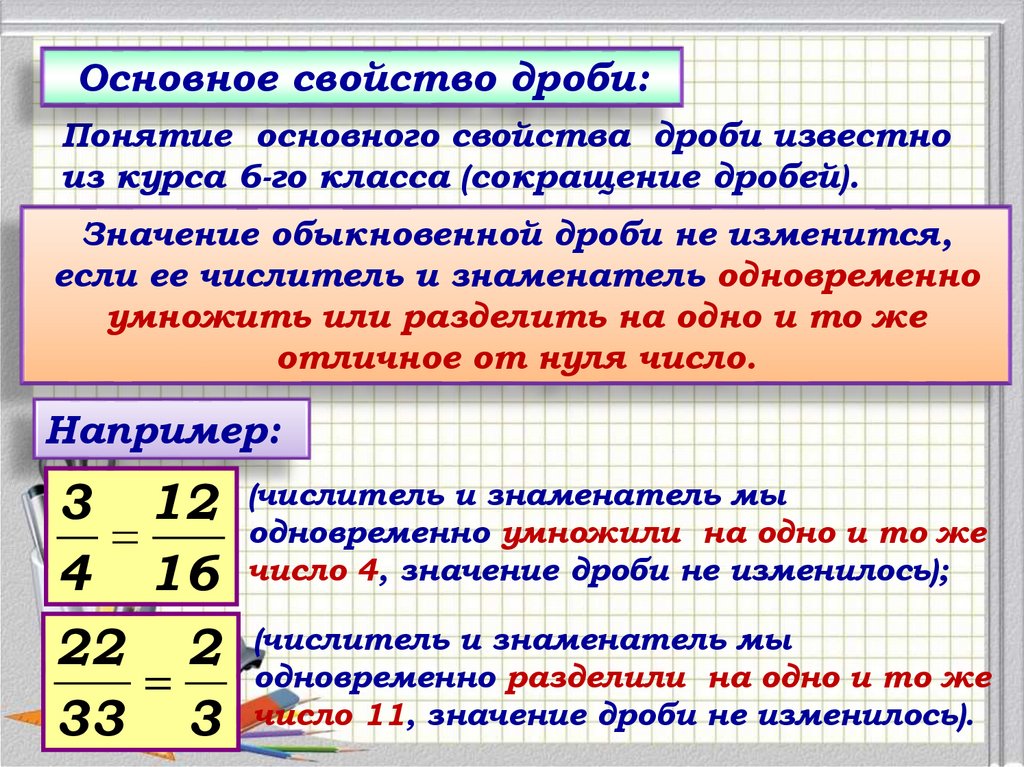
Основное свойство дроби:
Понятие основного свойства дроби известно
из курса 6-го класса (сокращение дробей).
Значение обыкновенной дроби не изменится,
если ее числитель и знаменатель одновременно
умножить или разделить на одно и то же
отличное от нуля число.
Например:
и знаменатель мы
3 12 (числитель
одновременно умножили на одно и то же
4 16 число 4, значение дроби не изменилось);
и знаменатель мы
22 2 (числитель
одновременно разделили на одно и то же
33 3 число 11, значение дроби не изменилось).

5.

Основное свойство дроби:
При умножении или делении числителя и
знаменателя алгебраической дроби на один и тот
же ненулевой многочлен, на одно и то же число,
не равное нулю, получается равная ей дробь
Основное свойство дроби можно записать так:
b ≠ 0, m ≠ 0, тогда
Например,
a b a b c
,
b
bc
а ma ma а
,
.
b mb mb b
a b c c .
a b d d

6.

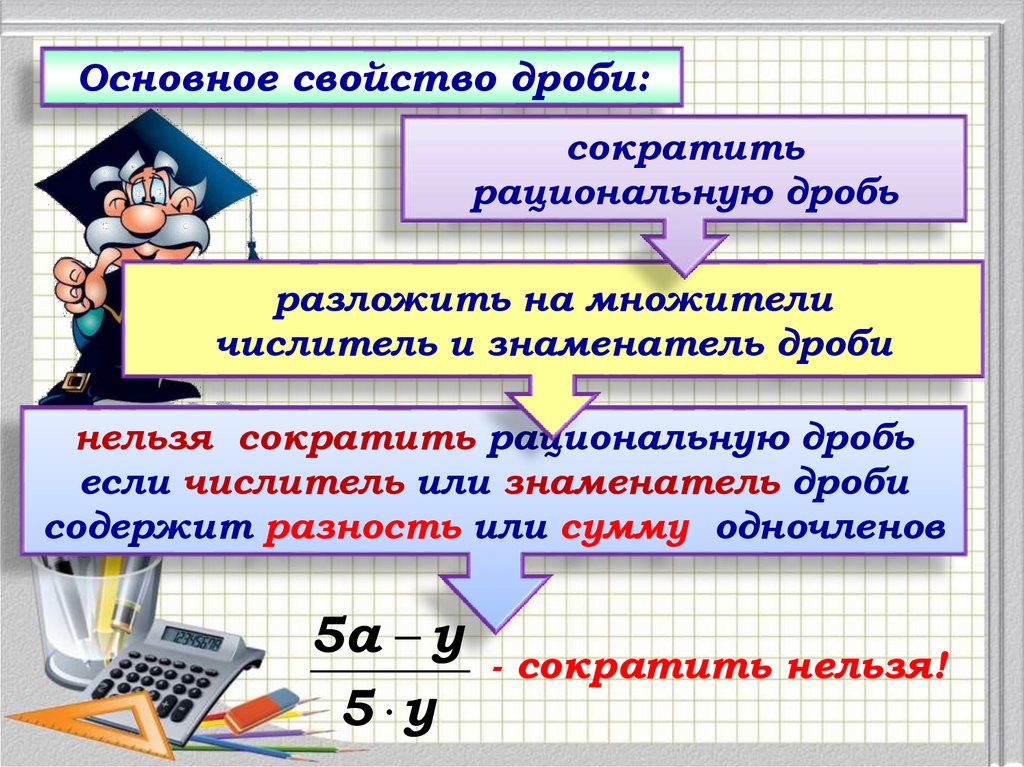
Основное свойство дроби:
сократить
рациональную дробь
разложить на множители
числитель и знаменатель дроби
нельзя сократить рациональную дробь
если числитель или знаменатель дроби
содержит разность или сумму одночленов
5a у
- сократить нельзя!
5 у

7.

Основное свойство дроби:
сократить
рациональную дробь
разложить на множители
числитель и знаменатель дроби
вынести общий
множитель за скобку
36а +12аb= 6a(6+2b)
14y² – 49y=7y(2y –7)
применить формулу
сокращенного
умножения
а² +2ab+b²= (а + b)²
а² – 2ab+b²= (а – b)²
а² – b² = (а – b)(а + b)

8.

Разложить на множители:
15а + 20ау= 5a(3 +4y)
2b³ – 6b²= 2b²(b – 3)
25 – x² = (5 – x)(5 + x)
a² – 49= (a – 7)(a + 7)
4c² – 9 = (2c – 3)(2c + 3)
x²+14x+49=
=(x+7)²=(x+7)(x+7)

9.

Сократите данные дроби:
4
1
2
1
1
12а b x 6 2 a a b x 2a x
а)
;
2 2
2
2
18a b y
6 3 a b y
3y
2
1
1
2
2
2
1
3x y 6x y
б)
3
2 2
3x y 12x y
2
2
2
1
3x y(1 2y) (1 2y)
.
2
3x y(x 4y) (x 4y)
1
2

10.

Сократите данные дроби:
4а х 4а х
в)
3
2 2
3
6а х 12а х 6а х
3
3
4а х (a х )
2
2
6а х (a 2а х х )
2
2
4а х (a х)(a x)
2
6а х (a х)
1
1
1
1
1
1
2 2 ах (a х)(a x) 2(a x)
.
2 3 ах (a х)(a x) 3(a x)

11.

Следствие из основного свойства дроби :
(изменение знаков у числителя и знаменателя)
a
a
;
b
b
a
a
;
b
b
a
a
;
b a
a b
a
a
;
a b
a b
a b (b a)
b a
;
c d
c d
c d
a b (a b)
a b
.
c d (d c)
d c
(a b) 2 (b a) 2 ;