Алгебраическая дробь. Сокращение дробей

1. Алгебраическая дробь. Сокращение дробей.

2.

Буквы могут принимать лишь допустимые
значения, т. е. такие значения, при которых
знаменатель этой дроби не равен нулю.
Для дроби
a
допустимыми
a a 1
являются все
значения а, кроме а = 0 и а = 1.
Найти допустимые значения букв,
3
;
а
4
;
b
a b
a 2
входящих
a 5
.
3 a
в дробь:

3.

Найти допустимые значения букв,
входящих в дробь:
4
2
x
0
1)
c 5
4)
x
c 5
m n
3
2)
m 3
p 1
5
)
2
m 3
p 1
n
3) 2
любое действительное
n
число
n 4

4. Допустимые значения переменных

• Какие значения может
принимать буква а?
Почему?
7а 8
а
7а 8
а 1

5. При каком значении переменой дроби не имеют смысла?

6.

• Алгебраическими дробями
называют выражения вида:
а 12 7 y 4
;
;
в q p
y
1 4 x( x 1) y
;
ab 5 y ( y 1) x

7. Основное свойство дроби.

а m a
b m b
Числитель и знаменатель
дроби можно умножить
(разделить) на одно и тоже
число.

8.

ОСНОВНОЕ СВОЙСТВО
ДРОБИ
a ac
,
b bc
b 0, c 0
Если числитель и знаменатель рациональной
дроби умножить на один и тот же ненулевой
многочлен, то получится равная ей дробь.
д в а т и п а з а д а н и й, при выполнении которых
применяется основное свойство дроби:
– приведение дробей к новому знаменателю;
– сокращение дробей.

9.

Основное свойство дроби
При умножении или делении числителя и знаменателя
алгебраической дроби на одно и то же число, не равное
нулю, получается равная ей дробь
Основное свойство дроби можно записать так:
b ≠ 0,
m ≠ 0, тогда
Правильно! А с
Можно сокращать
новыми дробями
алгебраическую
так:
дробь на общий
множитель
числителя и
знаменателя
дроби
a b c
a b d
а ma
,
b mb
c
.
d
ma а
.
mb b
Я это знаю!
Я же это знаю!
Это сокращение
дроби!
12 2
18 3

10.

Упражнения
3. Заполните пустые места так, чтобы равенство было
верным:
2
4
5c
b
b
; 2)
; 3)
3 2;
ab 3a b
3a
2 4
3 2
2 3
an
n
ab a b
6c d
3d
; 5)
; 6)
.2
5
6
8c d
5a n
5c
3a
1)
3
2
b
b
4)

11.

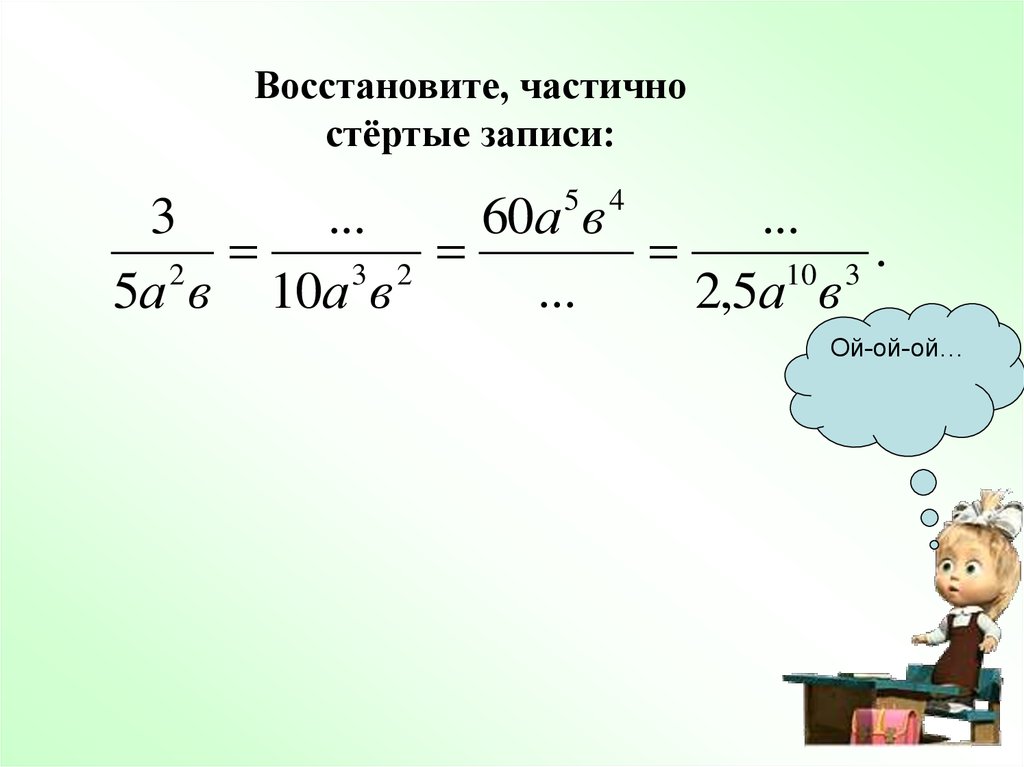
Восстановите, частично
стёртые записи:
3
...
60а в
...
.
2
3 2
10 3
...
5а в 10а в
2,5а в
5 4
Ой-ой-ой…

12. Найдите закономерность формирования дробей в ряду и определите следующую дробь

2
Найдите закономерность формирования
дробей в ряду и определите следующую
дробь
a a2
a3
A)
,
,
, ...
2
b ab a b
16
8
Б)
,
,
24 12
4
, ...
6

13. Как получена вторая дробь из первой?

3
Как получена вторая дробь из первой?
a a
b
b

14.

Разложите на множители:
1)7 14a 7(1 2a)
2)4a b 18b a 2ab(2a 9b)
2
2
3)36 c (6 c)(6 c)
2
4)16 z 81x (2 z 3x)(2 z 3x)(4 z 9 x )
4
4
2
2
5)4 4 y y (2 y) (2 y)(2 y)
2
2
6) y 8 ( y 2)( y 2 y 4)
3
2

15.

Найдите ошибки:
1. 4 у 3 х 3 х 4 у 8 у 2 9 у 2 ;
2.100m 4n 10m 2n 10m 2n ;
2
4
4
4
3. 4 x a 16 x 8ax a ;
2
2
2
2
4. 6a 9c 36a 108a c 18c
2
2
2
Мишка,
Мишка!
Помоги
мне
ошибки
найти!

16. Сократить дробь

12а в
2
4ав
2
2
m n
2
m mn
2

17. Сократите дробь

18.

Сократите дроби:
14 x 3 y 7 x 2
1)
2
22 xy
11 y
2
2
a 4b
(a 2b)( a 2b) a 2b
2)
2
2
(a 2b)
(a 2b)
a 2b
2
2
a
a
a
3) 2
a(a 3) a 3
a 3a
a 2 10ab 25b 2 (a 5b) 2 (5b a) 2
4)
5b a
5b a
5b a
5b a
2
2
2
3x 4 y
3x 4 y
9 x 24 xy 16 y
5)
2
2
9 x 16 y
(3x 4 y )(3x 4 y ) 3x 4 y

19.

К каждой дроби найти равную ей дробь,
используя соответствие число - буква
1)
а 2 ав
2
ав в
2х 3 у
;
2) 2
2
4х 9 у
3) а 6ав 9в
2
а 9в
2
2
2
Так,
так…
а
3
в
б)
а 3в
1
а)
;
2х 3 у
.
.
в)
а
в

20.

К каждой дроби найти равную ей дробь,
используя соответствие число - буква
1)
а 2 ав
2
ав в
2х 3 у
;
2) 2
2
4х 9 у
в)
а 9в
2
а
3
в
б)
а 3в
1
а)
;
2х 3 у
1)
3) а 6ав 9в
2
.
.
2)
а)
в)
3)
а
в
б)
2
2

21.

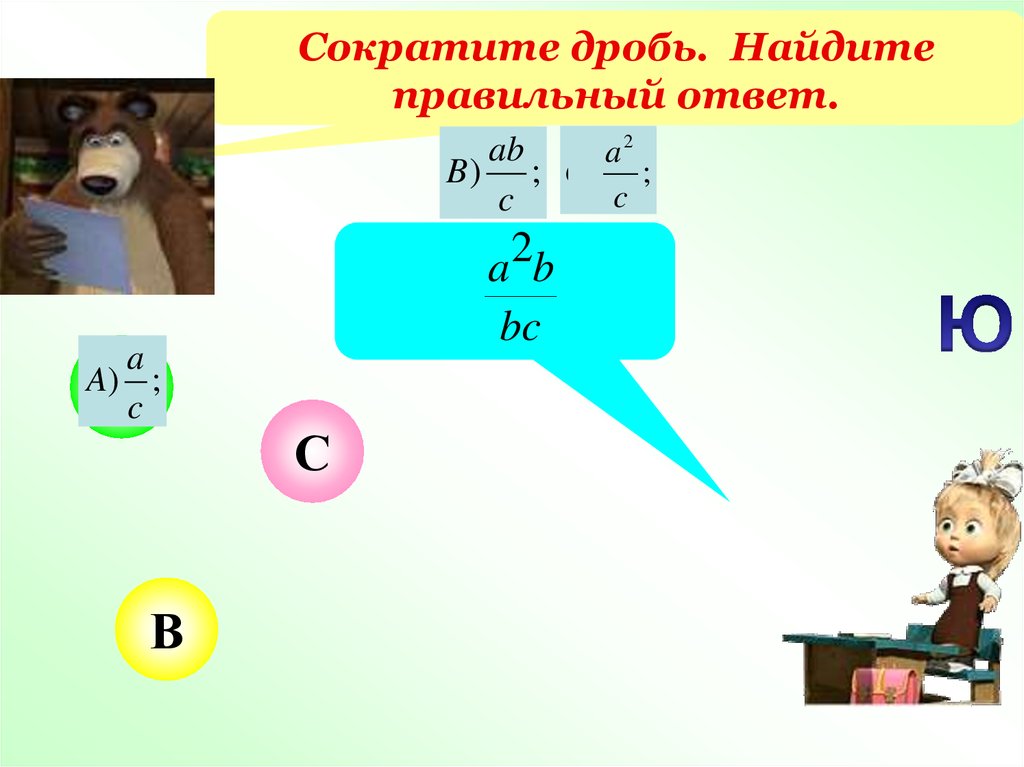
Сократите дробь. Найдите
правильный ответ.
ab
a2
B) ; C ) ;
c
c
a
AА
) ;
c
В
a 2b
bc
С

22.

Найдите правильный
ответ.
1
A) ;
2
B)
a b
; С) a b ;
2(a b)
a b
2a 2b
4a 4b
А
В
С

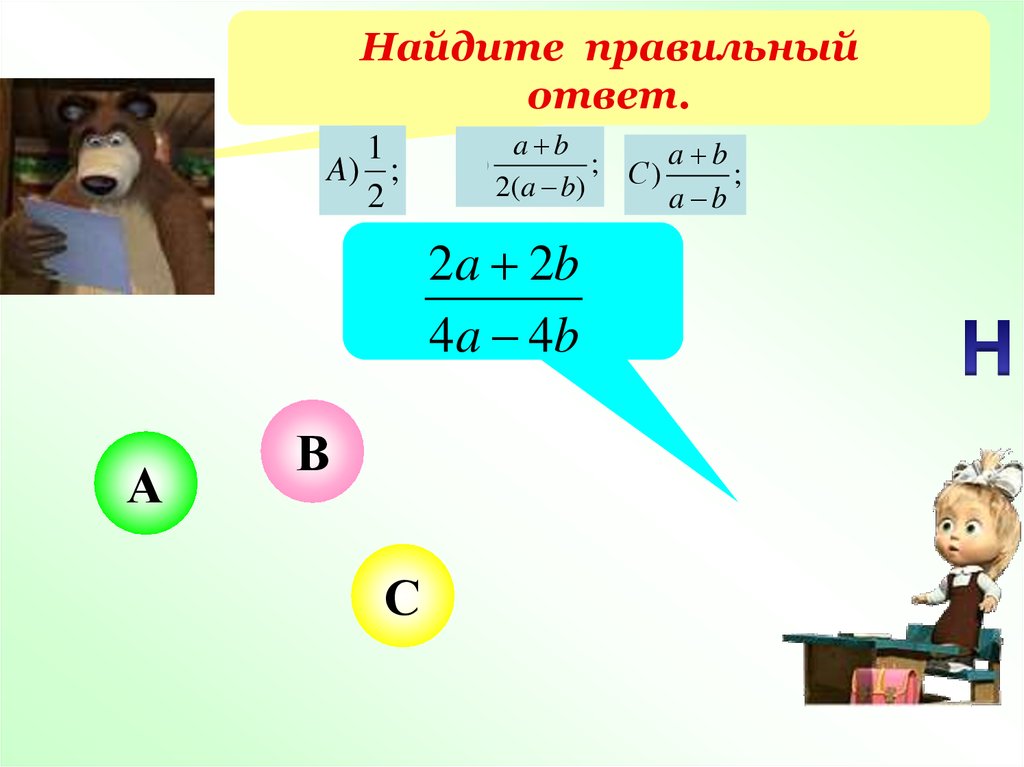
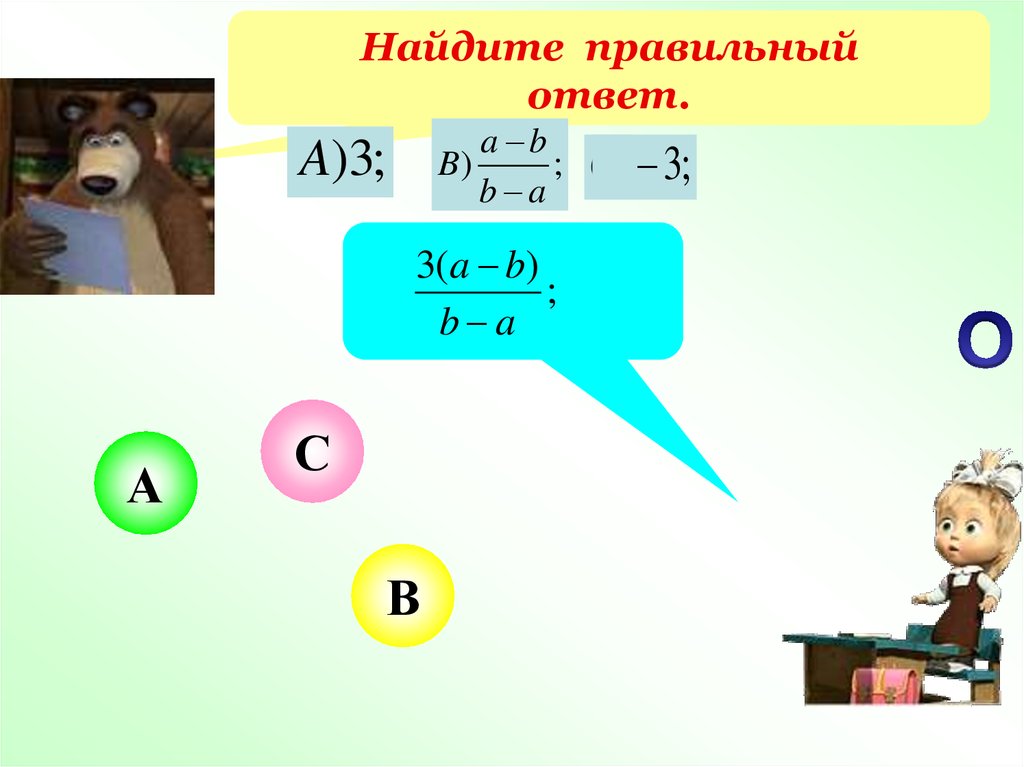
23.

Найдите правильный
ответ.
A)3;
B)
a b
;
b a
3(a b)
;
b a
А
С
В
C ) 3;

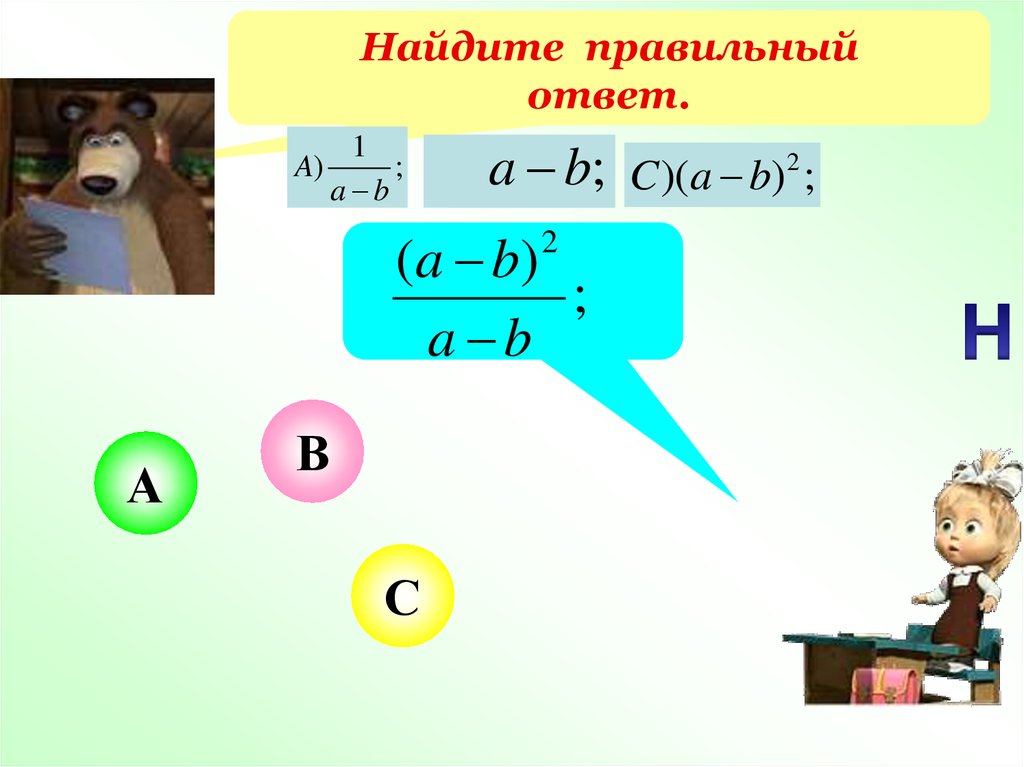
24.

Найдите правильный
ответ.
1
A)
;
a b
B )a b;
( a b)
;
a b
2
А
В
С
C )(a b) 2 ;

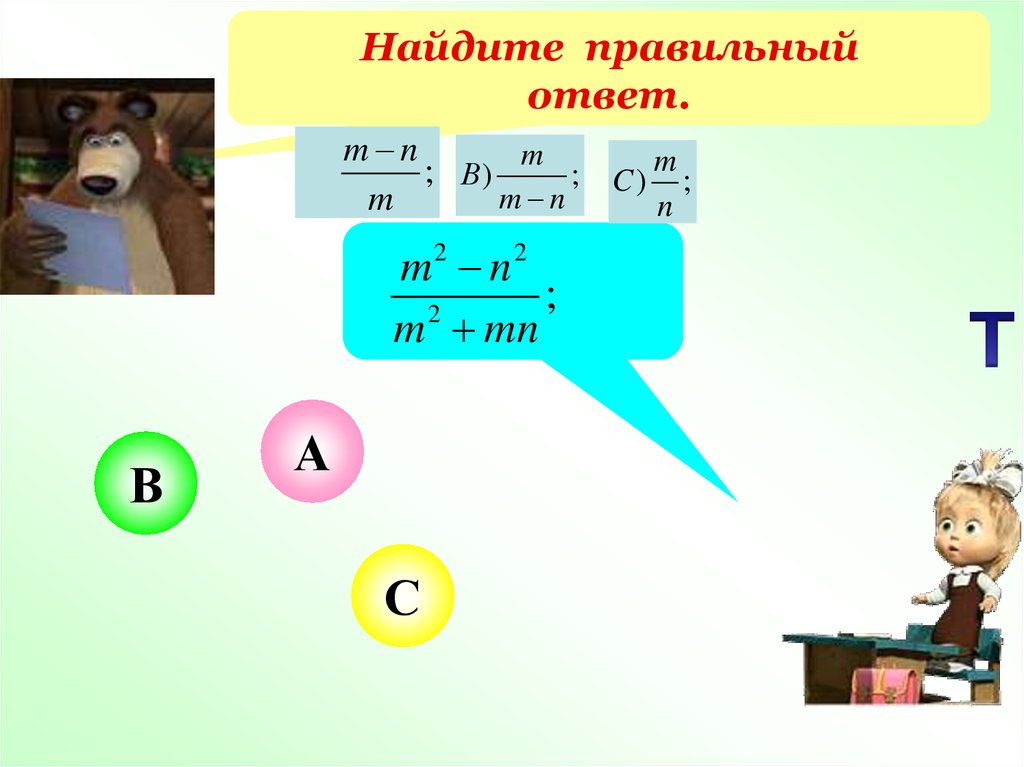
25.

Найдите правильный
ответ.
m n
m
А)
; В)
; C) m ;
m n
m
n
m n
;
2
m mn
2
В
А
С
2

26.

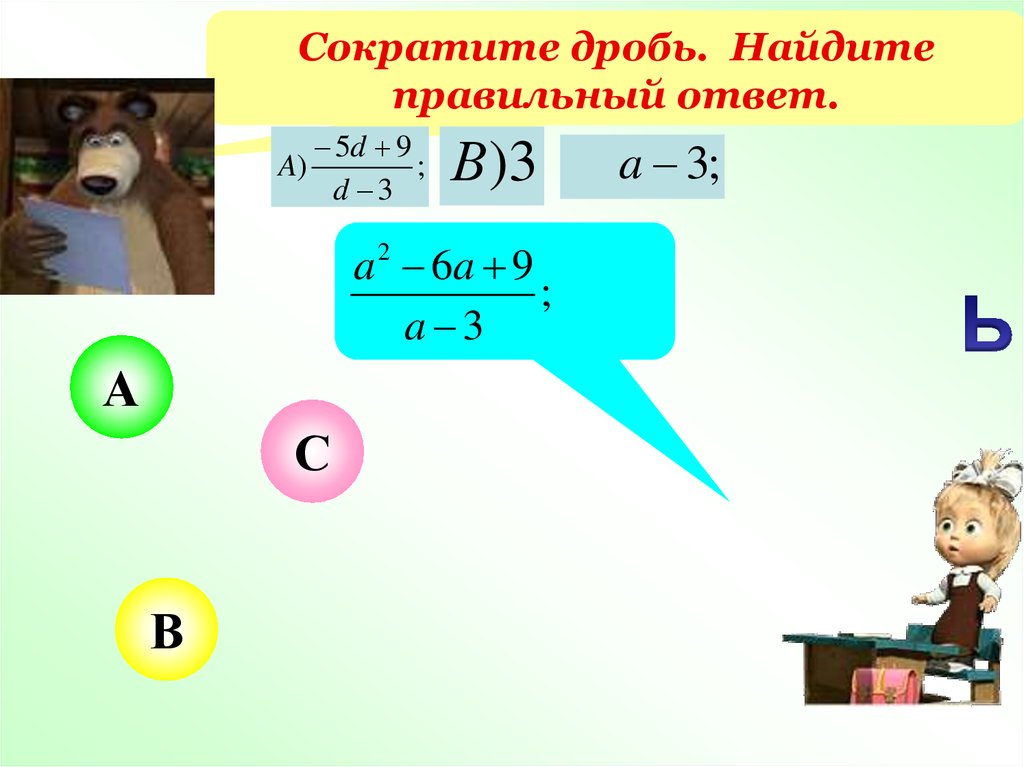
Сократите дробь. Найдите
правильный ответ.
5d 9
A)
;
d 3
В )3 С )a 3;
a 6a 9
;
a 3
2
А
С
В

27.

Сэр Исаак Ньютон - родился 4 января 1643 года в деревне
Вулсторп (графство Линкольншир), Англия. Великий
английский
физик,
математик
и
астроном.
Автор
фундаментального
труда
«Математические
начала
натуральной философии», в котором он описал закон
всемирного тяготения и так называемые Законы Ньютона,
заложившие основы классической механики. Разработал
дифференциальное и интегральное исчисление, теорию
цветности и многие другие математические и физические
теории.
a b
2(a b)
a 3
a2
c
m n
m
3
a b

28. Найдите значение алгебраической дроби, предварительно сократив ее:

x 4
x 2
2
при
х=10,
х=0,
х=5,
х=2.
• Всегда ли это возможно?
• Когда нет?

29. Упростить

а в
( а в )с
в
вс
а (в с )
а (в с )
( а в )с
(а в )d