лекция 7(2024)

1.

Лекция 7
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ
План:
1. Вектор. Основные понятия
2. Скалярное произведение
3. Векторное произведение
4. Смешанное произведение

2.

Опр. Вектором называется
направленный
отрезок прямой
Обозначают векторы символами
или AB , где А- начало, а B-конец
направленного отрезка.
В
А
a
a

3.

ВИДЫ ВЕКТОРОВ
1. Нулевой вектор
2. Коллинеарные векторы (сонаправленные и
противоположно направленные)
3. Равные векторы
4. Компланарные векторы

4.

Координаты вектора
Z
az
a
k
ay
ax
i
X
Y
j
i j k,
i j k 1.

5.

Определение.
Координатами вектора в пространстве называются его
проекции на координатные оси и записываются в виде
a ax , a y , az ,
где
a x пр x a , a пр a , a пр a .
y
y
z
z

6.

Любой вектор можно представить
в виде линейной комбинации базисных векторов:
a a xi a y j a z k .

7.

Основные формулы в координатной форме
1) Длина вектора
a a x2 a 2y a z2
2) Сумма векторов
a b ax bx , a y by , az bz
3) Произведение вектора
на число
ka kax , kay , kaz

8.

Основные формулы в координатной форме
4) Если заданы координаты
начала A и конца B вектора, то
AB x2 x1, y2 y1, z2 z1
5) Условие коллинеарности
двух векторов
ax a y az
bx by
bz

9.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Скалярное произведение двух векторов a
равное
a b a b cos
и
b
- это число,

10.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Свойства:
1) Если векторы a и b
ненулевые:
a b 0
2)
a a
3)
a b b a
4)
(a b ) c a c b c
5)
(a b ) ( a ) b a ( b )
2
2
Скалярный квадрат
вектора равен
квадрату его модуля
a b

11.

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ В КООРДИНАТНОЙ
ФОРМЕ
a b x1 x2 y1 y 2 z1 z2
Из формулы скалярного произведения векторов следует формула
для нахождения угла между векторами:
cos
a b
a b
x1 x 2 y 1 y 2 z1 z2
x12 y 12 z12 x 22 y 22 z22

12.

a b
cos
a b
x1 x 2 y 1 y 2 z1 z2
x12 y 12 z12 x 22 y 22 z22
Найти косинус угола между векторами:
a i 2 j 3k
b 6i 4 j 2k

13.

Найти косинус угола между векторами:
a b 1 6 2 4 3 2 8
a i 2 j 3k
b 6i 4 j 2k
a 12 22 3 2 14
b 6 4 2 56 2 14
8
2
cos
14 2 14 7
2
2
2

14.

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
левой
Тройка некомпланарных векторов a, b, c называется правой
если наименьший поворот с конца третьего вектора c от первого
вектора a ко второму вектору b виден против
часовой стрелки
по
c
c
b
a
a
c a b
b
Векторным произведением вектора a на вектор b называется
вектор c , определяемый следующим образом:
c a b sin( a ; b ) .
c a; c b
Вектор c направлен так, что тройка векторов
a; b ; c - правая.

15.

СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
1) Модуль векторного произведения равен площади
параллелограмма, построенного на перемножаемых векторах
S c a b sin
c
b
a
2)
a b 0
a II b

16.

СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ
3) a b b a
4)
a b c a b a c
5) (a b ) ( a ) b a ( b )
6)
a a 0 - векторный квадрат равен нулю для любого вектора

17.

ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ В КООРДИНАТАХ
i
j k
a b x1 y 1 z1
x 2 y 2 z2

18.

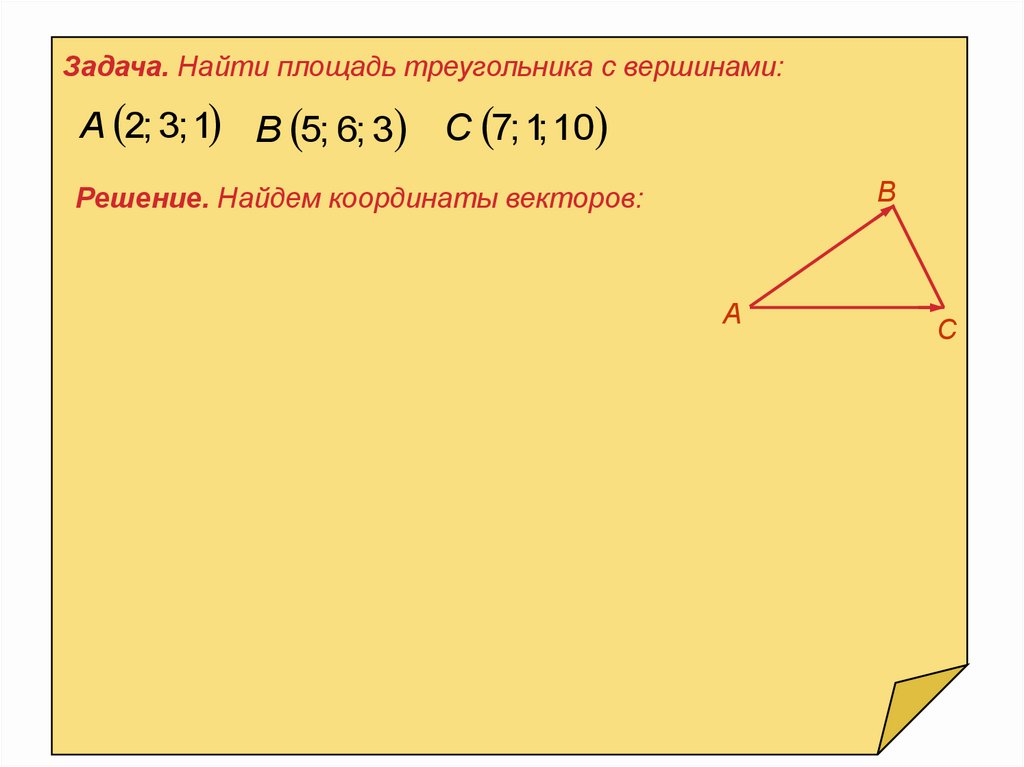
Задача. Найти площадь треугольника с вершинами:
A 2; 3; 1 B 5; 6; 3
C 7; 1; 10
В
Решение. Найдем координаты векторов:
А
С

19.

Задача. Найти площадь треугольника с вершинами:
A 2; 3; 1 B 5; 6; 3
C 7; 1; 10
В
Решение. Найдем координаты векторов:
AB 5 2,6 3,3 1 3 ,3 ,2
AC 7 2,1 3,10 1 5, 2, 9
А
1
S a b
2
i
j k
a b 3 3 2 31i 17 j 21k
5 2 9
1
S
312 ( 17)2 ( 21)2
2
1
1691 20,6
2
С

20.

СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Смешанным произведением трех векторов a, b, c называется
произведение, которое получается скалярным умножением
векторного произведения двух векторов на третий вектор, т.е.
произведение вида:
a b c
Смешанное произведение представляет собой скаляр.
V | a b c |
c
b
a

21.

Законы смешанного произведения
1)
Сочетательный закон :
a b c a (b c )
Учитывая сочетательный закон, смешанное произведение
обозначают: (a , b , c ) или a b c .

22.

Законы смешанного произведения
2)
Закон круговой переместительности:
c
b
a b c b c a c a b a c b c b a b a c
a
При перестановке множителей не нарушающей их кругового
порядка, смешанное произведение не меняется, при
перестановке же множителей, нарушающей круговой
порядок, смешанное произведение меняет свой знак

23.

3) Распределительный закон
a a b c a b c a b c
1
4)
2
abc 0
1
2
a ; b ; c компланарны

24.

Смешанное произведение в координатах
x1 y 1 z1
a b c x 2 y 2 z2
x3 y 3 z3

25.

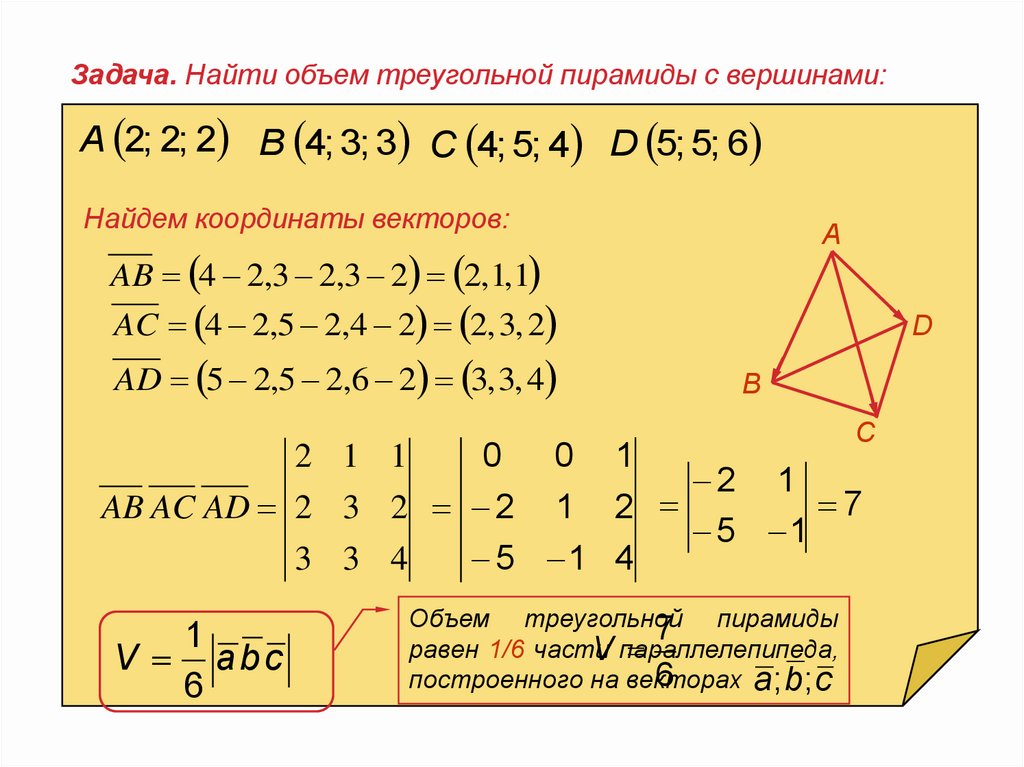
Задача. Найти объем треугольной пирамиды с вершинами:
A 2; 2; 2 B 4; 3; 3 C 4; 5; 4 D 5; 5; 6
Найдем координаты векторов:
А
D
В
С
1
V abc
6
Объем треугольной
7 пирамиды
равен 1/6 части
V параллелепипеда,
6
построенного на векторах
a; b ; c

26.

Задача. Найти объем треугольной пирамиды с вершинами:
A 2; 2; 2 B 4; 3; 3 C 4; 5; 4 D 5; 5; 6
Найдем координаты векторов:
А
AB 4 2,3 2,3 2 2,1,1
AC 4 2,5 2,4 2 2, 3, 2
AD 5 2,5 2,6 2 3, 3, 4
D
В
С
2 1 1
0
0 1
2 1
7
AB AC AD 2 3 2 2 1 2
5 1
3 3 4
5 1 4
1
V abc
6
Объем треугольной
7 пирамиды
равен 1/6 части
V параллелепипеда,
6
построенного на векторах
a; b ; c