Лекция_1017_С_1к_1с_Законы_сохранения_5

1.

Физика 1 курс, 1 семестр
Лекция 10. Физические основы механики
Законы сохранения:
- Закон сохранения момента
импульса
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

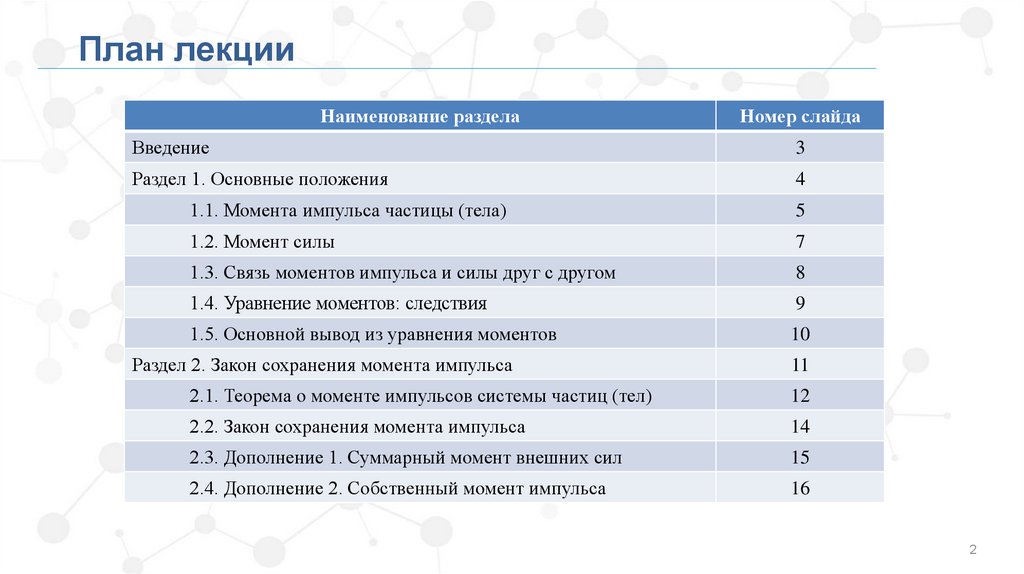
План лекции
Наименование раздела
Номер слайда
Введение
3
Раздел 1. Основные положения
4
1.1. Момента импульса частицы (тела)
5
1.2. Момент силы
7
1.3. Связь моментов импульса и силы друг с другом
8
1.4. Уравнение моментов: следствия
9
1.5. Основной вывод из уравнения моментов
10
Раздел 2. Закон сохранения момента импульса
11
2.1. Теорема о моменте импульсов системы частиц (тел)
12
2.2. Закон сохранения момента импульса
14
2.3. Дополнение 1. Суммарный момент внешних сил
15
2.4. Дополнение 2. Собственный момент импульса
16
2

3.

Введение
10-ая лекция завершает изучение раздела «Законы сохранения в механике». Ранее были
рассмотрены следующие темы:
-
понятие импульса, был получен закон сохранения импульса (в 6-ой лекции),
понятие кинетической энергии частицы и понятие работы (в 7-ой лекции),
понятие потенциальной энергии частицы во внешнем поле сил (в 8-ой лекции),
понятие потенциальной энергии взаимодействия частиц (тел), закон сохранения полной
механической энергии и условия равновесия механической системы (в 9-ой лекции).
В 10-ой лекции будет сформулирован закон сохранения момента импульса, который
замыкает «великолепную тройку» законов сохранения в механике и, в целом, в физике.
Важную роль закон сохранения момента импульса играет в квантовой механике.
3

4.

Раздел 1. Основные положения
4

5.

1. Основные положения
1.1. Момент импульса частицы (тела)
Рассмотрим частицу массой m в произвольной системе координат с
точкой отсчёта О. Положение частицы будем характеризовать
соответствующим радиусом-вектором r, соединяющим точку О и точку
расположения частицы. В таком случае положение осей координат не
имеет значения и они указываться на рисунке не будут.
Пусть частица обладает импульсом p = m∙v – вектор, направление
которого может быть произвольным относительно радиус-вектора r.
Вектора p и r образуют между собой угол α.
Определение. Момент импульса частицы (тела) М относительно
точки О – это векторное произведение векторов r и p:
M = [r p]
Другие формы записи: M = [r х p] или: M = [r,p]
Модуль вектора М – скалярная величина, определяется так:
|M| = M = r∙p∙sinα = l∙p.
где l – плечо вектора р относительно точки О, скалярная величина:
l = r∙sinα – см. рисунок.
p
О
r
l
α
m
Плоский рисунок для определения
момента импульса М
5

6.

1. Основные положения
1.1. Момент импульса частицы (тела) - продолжение
Повторим определение момента импульса:
M = [r p] – векторное произведение
В соответствии со свойствами векторного произведения двух
векторов:
- Вектор М прикладывается к точке О, относительно которой этот
вектор рассчитывается, а не к самой частице (телу).
- Вектор М перпендикулярен и вектору r, и вектору p, т.е. он
перпендикулярен плоскости, в которой эти два вектора находятся.
Направление вектора М определяется по «правилу буравчика». В
данном случае – «сквозь плоскость экрана, на нас» - см. рисунок.
Нарисуйте взаимное расположение векторов r и p, при котором вектор М будет
направлен «от нас», т.е. «за экран». В этом случае, на рисунке стрелка М будет
направлена вниз.
Замечание. В учебной и научной литературе используются иные названия момента
импульса М: момент количества движения, механический момент, угловой момент,
просто момент.
M
О
p
r
α
m
Рисунок в изометрии для
определения момента импульса М
6

7.

1. Основные положения
1.2. Момент силы
Так же, как вектор импульса р, сила F, действующая на тело массой m, это вектор, приложенный к самому телу. Направления векторов р и F, в
общем случае, могут не совпадать (приведите пример).
Тогда момент силы N можно определить так же, как момент импульса
M – через векторное произведение:
N = [r F] – см. рисунок.
В соответствии со свойствами векторного произведения двух векторов:
- Вектор N прикладывается к точке О, относительно которой этот вектор
рассчитывается, а не к самой частице (телу).
- Вектор N перпендикулярен и вектору r, и вектору p, т.е. он
перпендикулярен плоскости, в которой эти два вектора находятся.
Направление вектора N определяется по «правилу буравчика». В
данном случае – «сквозь плоскость экрана, на нас» - см. рисунок.
Модуль вектора момента силы есть:
|N| = N = r∙F∙sinα = l∙F.
l = r∙sinα – плечо силы относительно точки О, скалярная величина.
N
О
r
F
l
α
m
Рисунок в изометрии для
определения момента силы N
7

8.

1. Основные положения
1.3. Связь моментов импульса и силы между собой
Продифференцируем момент импульса M по времени: