Лекция_617_С_1к_1с_Законы_сохранения_1

1.

Физика 1 курс, 1 семестр
Лекция 6. Физические основы механики
Законы сохранения:
- Закон сохранения импульса
В.И. Читайкин
кандидат физико-математических наук
доцент

2.

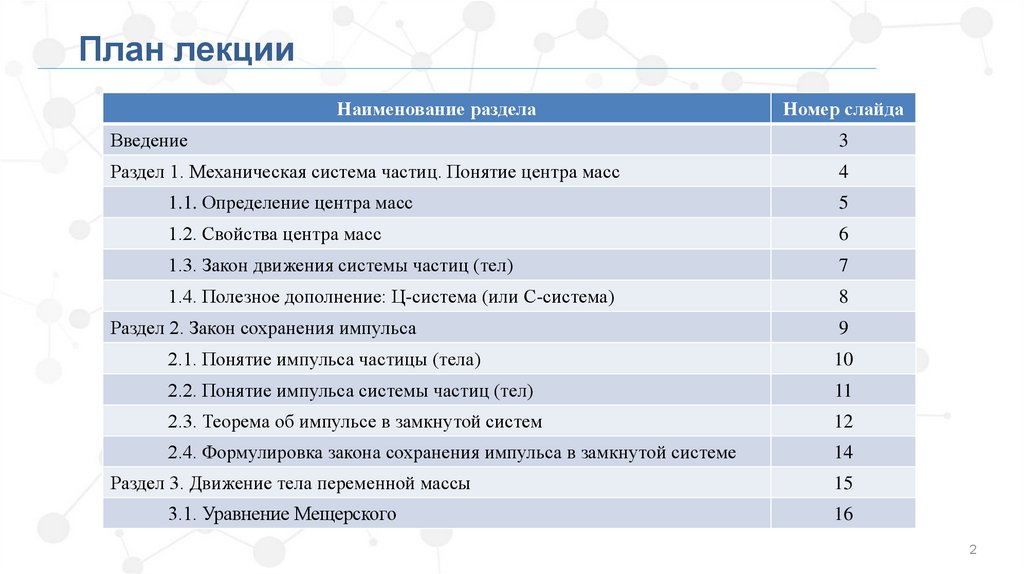
План лекции
Наименование раздела
Номер слайда
Введение
3
Раздел 1. Механическая система частиц. Понятие центра масс
4
1.1. Определение центра масс
5
1.2. Свойства центра масс
6
1.3. Закон движения системы частиц (тел)
7
1.4. Полезное дополнение: Ц-система (или С-система)
8
Раздел 2. Закон сохранения импульса
9
2.1. Понятие импульса частицы (тела)
10
2.2. Понятие импульса системы частиц (тел)
11
2.3. Теорема об импульсе в замкнутой систем
12
2.4. Формулировка закона сохранения импульса в замкнутой системе
14
Раздел 3. Движение тела переменной массы
15
3.1. Уравнение Мещерского
16
2

3.

Введение
6-ая лекция открывает новый (после «Кинематики» и «Динамики») раздел нашего курса – законы
сохранения в механике. Смысл таких законов столь же прост, как и важен. А именно:
в сложном, подчас запутанном мире физических процессов, когда меняются все параметры тела
(координаты, скорости, ускорения) в результате взаимодействия с другими телами, когда меняются силы и
другие условия, когда эти изменения происходят под действием только того, как сложились все условия в
данной точке и в данный момент времени и, казалось бы, не поддаются какому-либо обобщению –
тем не менее, во всём этом, казалось бы, непредсказуемом многообразии явлений и событий
существуют физические величины, которые остаются неизменными. Таких величин немного – три:
импульс, энергия, момент импульса.
Это фундаментальное положение – существование неизменных величин – было установлено в XVIIIXIX в.в., оно выполняется всегда и везде, в любом физическом, в любом природном процессе. В том
числе, в химическом, в биологическом, геологическом и других процессах. В этих случаях утверждение о
неизменности некоторых параметров имеет свою, специфическую формулировку.
В лекции 6 будет рассмотрен один из трёх законов сохранения в механике: закон сохранения импульса.
В начале лекции мы вернёмся к понятию «механическая система частиц», введённому в 3-ей лекции,
раздел 3, и дополним его важным понятием центра масс. Это понятие часто используется в дальнейшем, в
том числе, при рассмотрении законов сохранения.
3

4.

Раздел 1. Механическая система частиц.
Понятие центра масс
4

5.

1. Механическая система частиц. Понятие центра масс
1.1. Определение центра масс
Напомню (см. лекция 3, раздел 3), механическая система частиц – это совокупность частиц (тел),
выделенная в рамках решаемой задачи и рассматриваемая как единое целое.
Пусть система частиц состоит из n частиц, масса каждой частицы mi.
Каждая i-ая частица может быть описана своим радиус-вектором ri,
проведенным из одного и того же центра координат (точка О), выбранного
произвольно (на рисунке, для простоты, оси координат не показаны).
Тогда можно рассчитать «средний» радиус-вектор с учётом масс частиц.
m=
По физическому смыслу величина rc – это радиус-вектор точки С, в которой сосредоточена вся масса
системы частиц m. Точка С – это точка центра масс рассматриваемой механической системы частиц.
Определение: Центр масс (или – центр инерции) системы материальных точек – это
воображаемая точка С, с массой равной сумме масс всех частиц.
Положение точки С характеризует распределение масс частиц в механической системе. Координаты
центра масс – важный параметр механической системы частиц (тел).
5

6.

1. Механическая система частиц. Понятие центра масс
1.2. Свойства центра масс
1. Положение центра масс (точка С) НЕ ОБЯЗАТЕЛЬНО должно совпадать с положением одной
из реальных частиц. Точка С может оказаться «между» реальными точками, как это показано на
рисунке на предыдущем слайде, т.е. быть виртуальной, воображаемой. В таком случае в точке С нет
реальной частицы.
Более того, точка С может даже находиться за пределами системы частиц.
Самостоятельно: приведите пример такого положения точки С (нарисуйте).
С
2. Положение точки центра масс (точки С) в пространстве
не изменится, даже если изменится положение точки начала
координат: точка О
точка О' (см. рис. справа; оси координат вновь
не показаны).
В этом случае изменится лишь радиус-вектор: rc ≠ r'с, – т.к.
он будет проведен из разных начальных точек: из точки О или
из точки О', но сама точка С останется на прежнем месте.
Попробуйте доказать это самостоятельно, используя рисунок.
6

7.

1. Механическая система частиц. Понятие центра масс
1.3. Закон движения системы частиц (тел)
Сколь угодно сложная механическая система частиц (тел) может быть описана двумя параметрами:
- положением центра масс этой системы (точка С) с соответствующим радиусом-вектором rc и
- массой m равной сумме масс всех частиц этой системы.
Тогда движение системы частиц – это движение центра масс этой системы, т.е. движение
материальной точки, в которой сосредоточена масса всей системы частиц и на которую действует сила,
равная геометрической (векторной) сумме всех внешних сил, действующих на системы. Это – закон
движения центра масс механической системы частиц.
Практическое следствие. Для расчёта движения тела любой
сложной формы (например, витрувианский человек Леонардо или
булыжник неопределённой формы) нужно заменить это тело
материальной точкой, расположенной в центре масс этого тела.
Для этого необходимо:
1. Рассчитать положение центра масс.
2. Всю массу тела сосредоточить в центре масс.
3. Все действующие на тело силы приложить к центру масс.
Тогда уравнение движение центра масс будет совпадать с
уравнением движения системы частиц (тела). Покажите это с использованием определения центра масс.
7

8.

1. Механическая система частиц. Понятие центра масс
1.4. Полезное дополнение: Ц-система (или С-система)
Решение задачи с несколькими движущимися частицами
(телами) существенно упростится, если точка О
соответствующей системы координат (системы отсчёта) будет
помещена в точку С – центр масс рассматриваемых частиц
(тел).
Определение: Ц-система (или С-система) – это такая
система отсчёта (система координат), в которой центр масс
покоится.
Причина этого в том, что полный импульс частиц (тел) в
Ц-системе всегда равен нулю, т.к. центр масс в «собственной»
системе отсчёта (в Ц-системе) всегда покоится: VC = 0.
Другими словами, любая система частиц (тел) как целое
покоится в своей Ц-системе в течение всего рассматриваемого
времени.
y
C
O
VC = 0
x
z
8

9.

Раздел 2. Закон сохранения импульса
9

10.

2. Закон сохранения импульса
2.1. Понятие импульса частицы (тела)
Определение: импульс материальной точки (частицы, тела) – это вектор p, рассчитываемый как
произведение массы точки (частицы, тела) m на её скорость v:
p = m∙v.
Масса m – скалярная величина, скорость v – векторная величина.
Вектор импульса точки (частицы, тела) р всегда направлен так же, как и вектор скорости v.
Второй закон Ньютона (основной закон динамики) для одной частицы можно записать через
импульс p:
F = m∙a = m∙(dv/dt) = d(mv) / dt= dp / dt.
Отсюда следует, что:
- Если F = 0, то импульс не изменяется во времени (p = const);
- Если сила изменяется во времени, то приращение импульса за время ∆t = t2 – t1 составит: