Similar presentations:
Тренажер по графикам функций
1.
Тренажер пографикам функций
2.
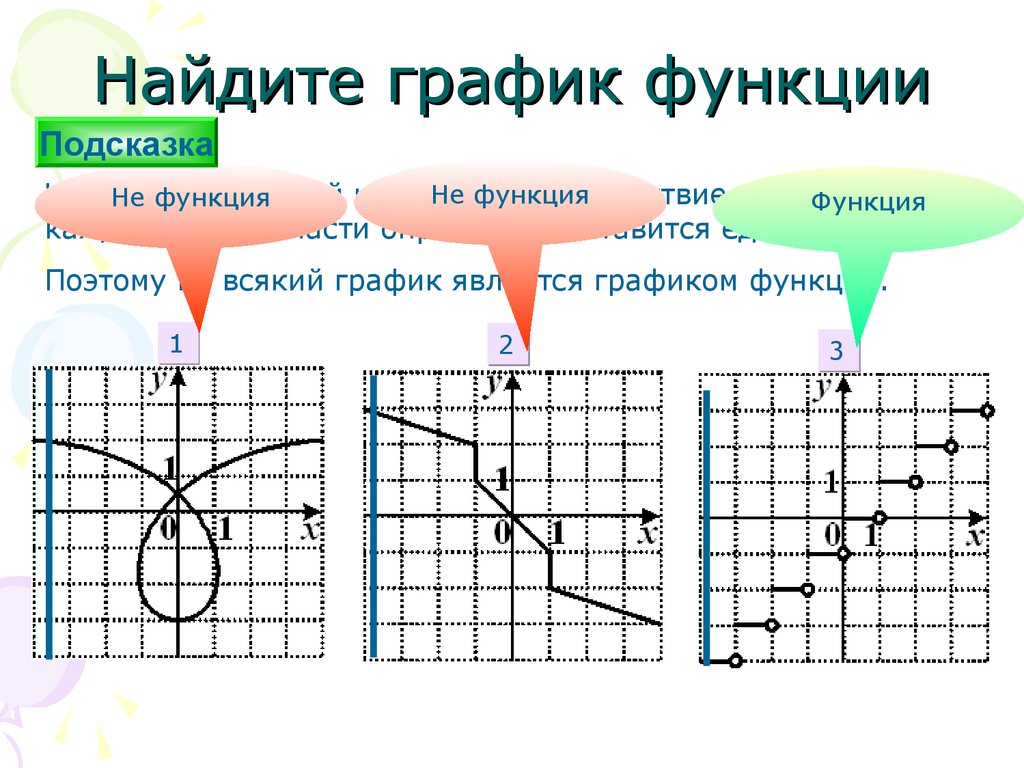
Найдите график функцииПодсказка
Не функция
Числовой
функцией называется
соответствие, при Функция
котором
Не функция
каждому х из области определения ставится единственное у.
Поэтому не всякий график является графиком функции.
1
2
3
3.
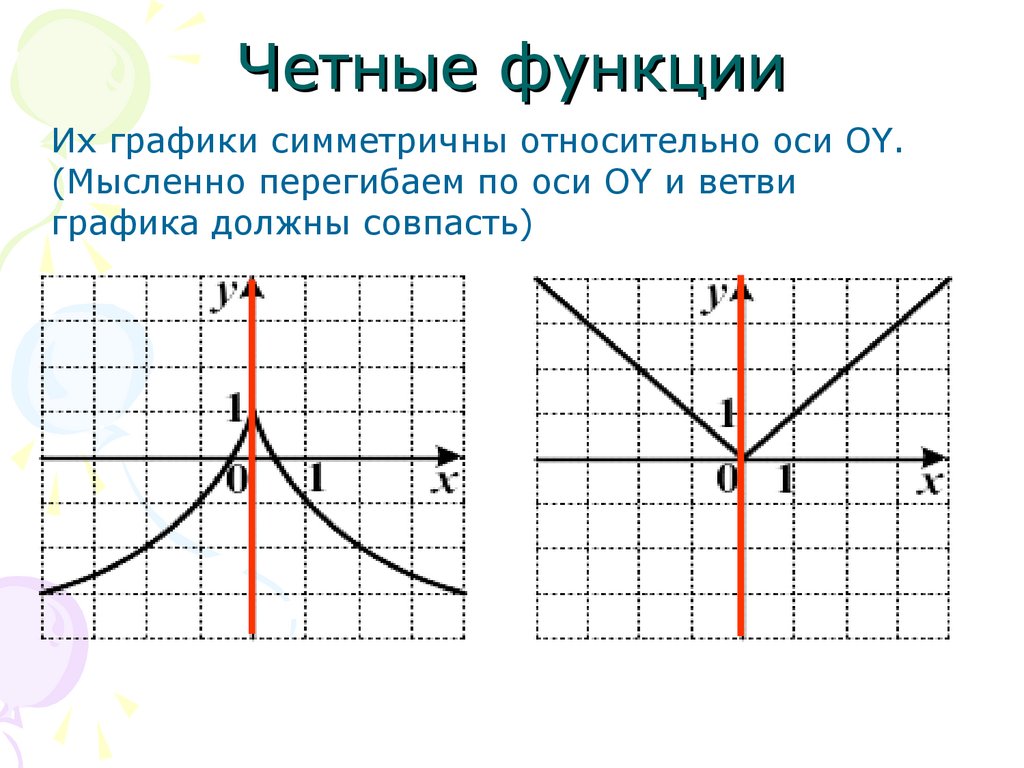
Четные функцииИх графики симметричны относительно оси OY.
(Мысленно перегибаем по оси OY и ветви
графика должны совпасть)
4.
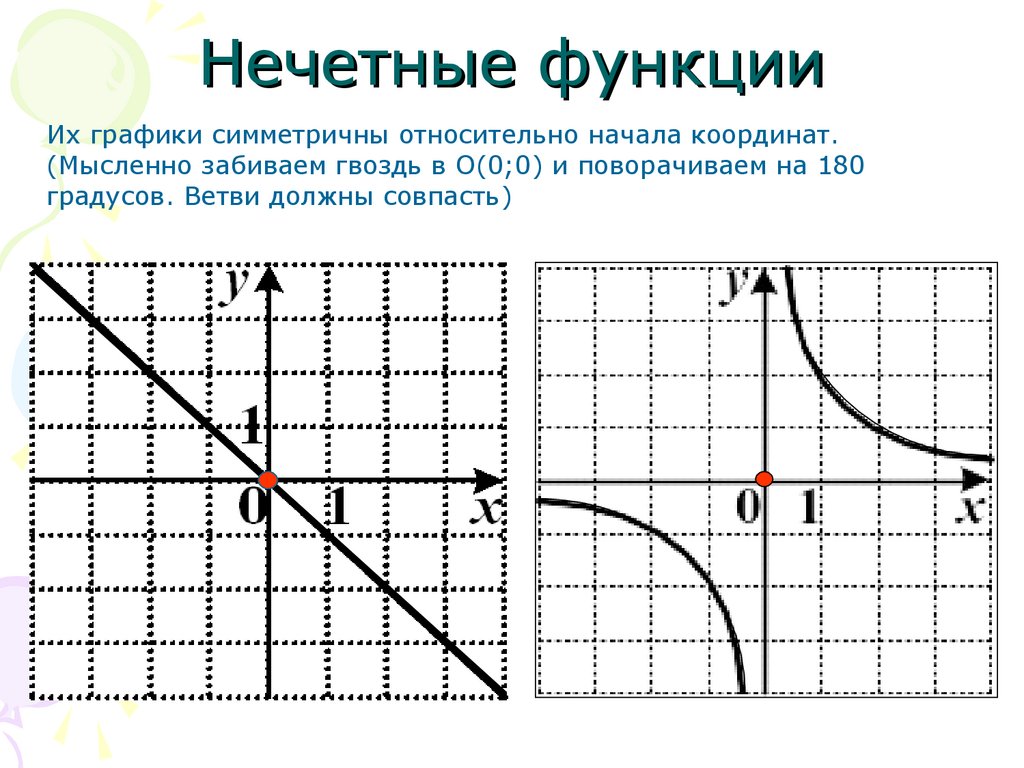
Нечетные функцииИх графики симметричны относительно начала координат.
(Мысленно забиваем гвоздь в O(0;0) и поворачиваем на 180
градусов. Ветви должны совпасть)
5.
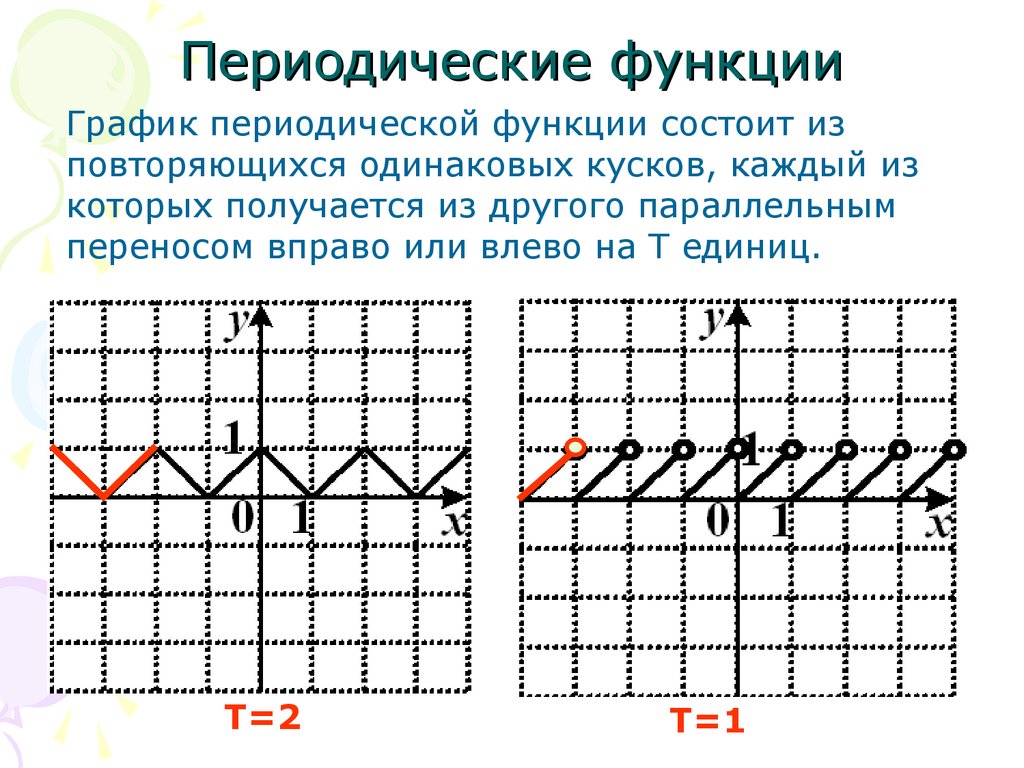
Периодические функцииГрафик периодической функции состоит из
повторяющихся одинаковых кусков, каждый из
которых получается из другого параллельным
переносом вправо или влево на Т единиц.
Т=2
Т=1
6.
Чтение графиковфункций
Полное исследование
функции по графику
7.
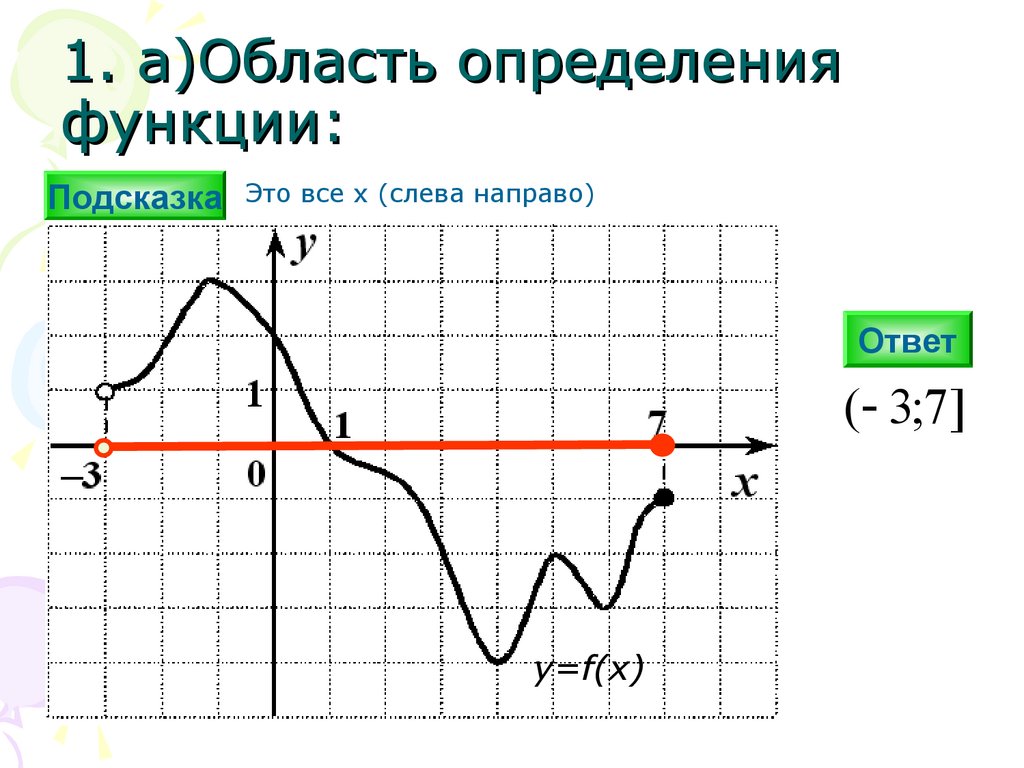
1. а)Область определенияфункции:
Подсказка Это все х (слева направо)
Ответ
( 3;7]
y=f(x)
8.
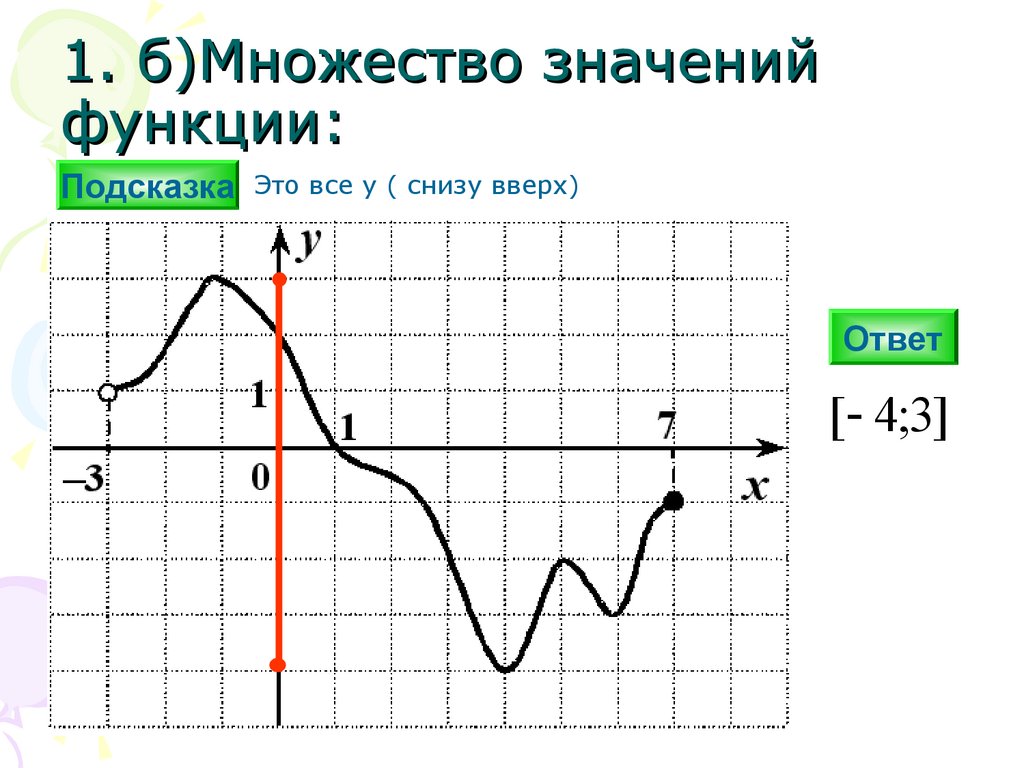
1. б)Множество значенийфункции:
Подсказка Это все y ( снизу вверх)
Ответ
[ 4;3]
9.
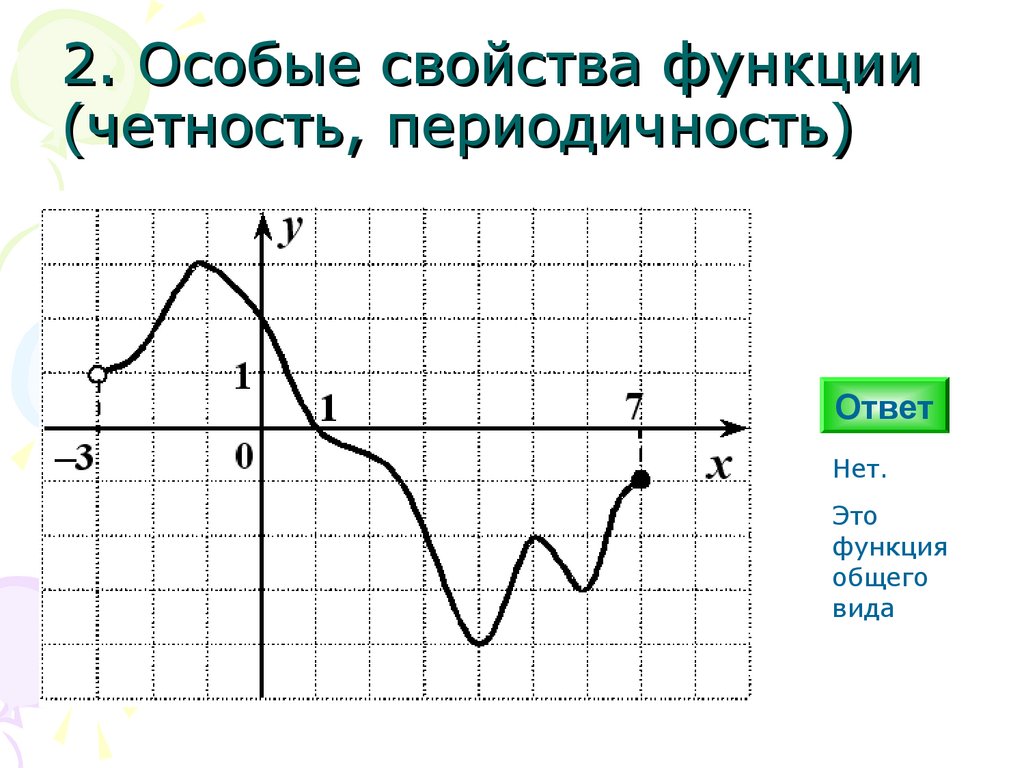
2. Особые свойства функции(четность, периодичность)
Ответ
Нет.
Это
функция
общего
вида
10.
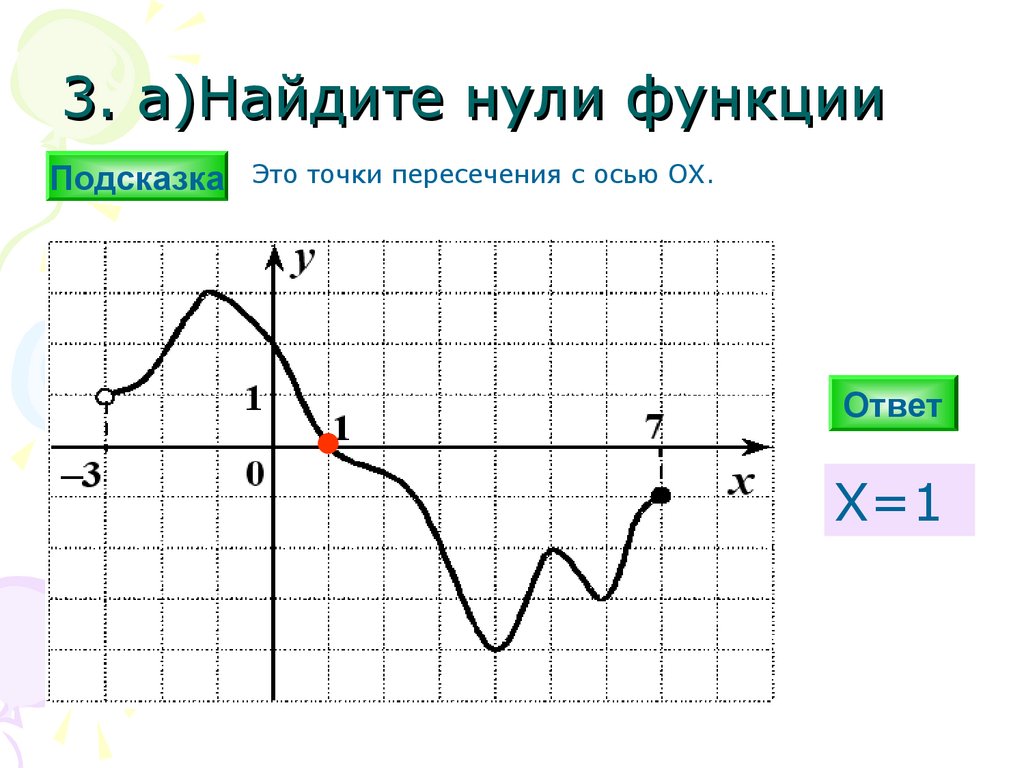
3. а)Найдите нули функцииПодсказка
Это точки пересечения с осью ОХ.
Ответ
Х=1
11.
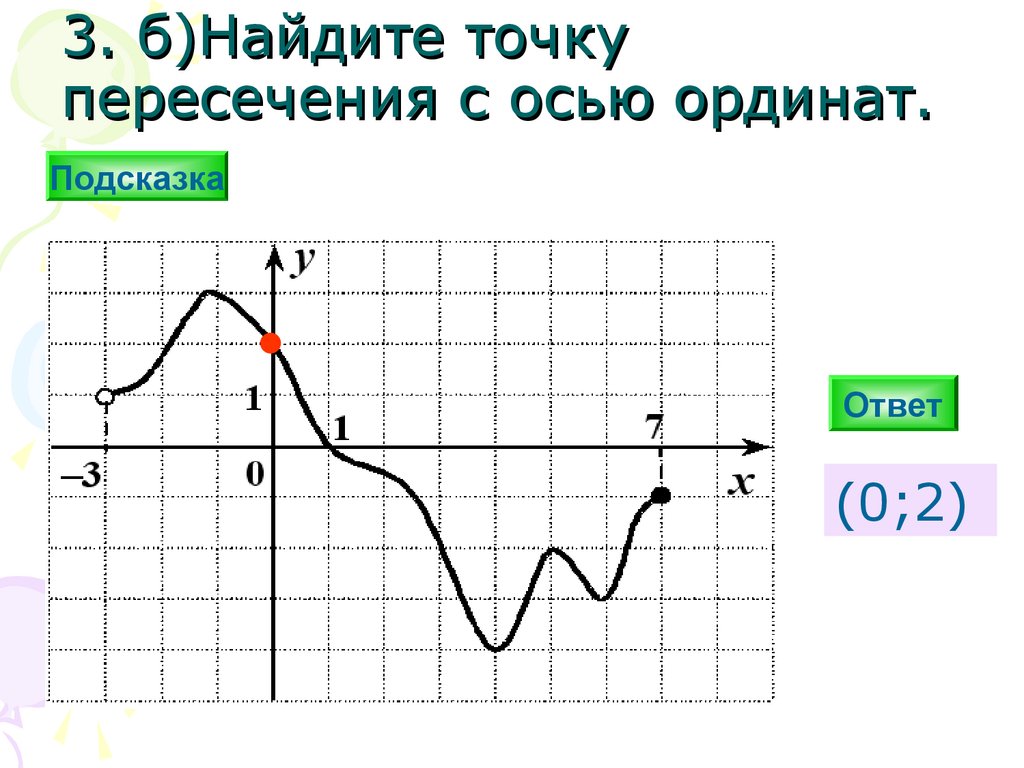
3. б)Найдите точкупересечения с осью ординат.
Подсказка
Ответ
(0;2)
12.
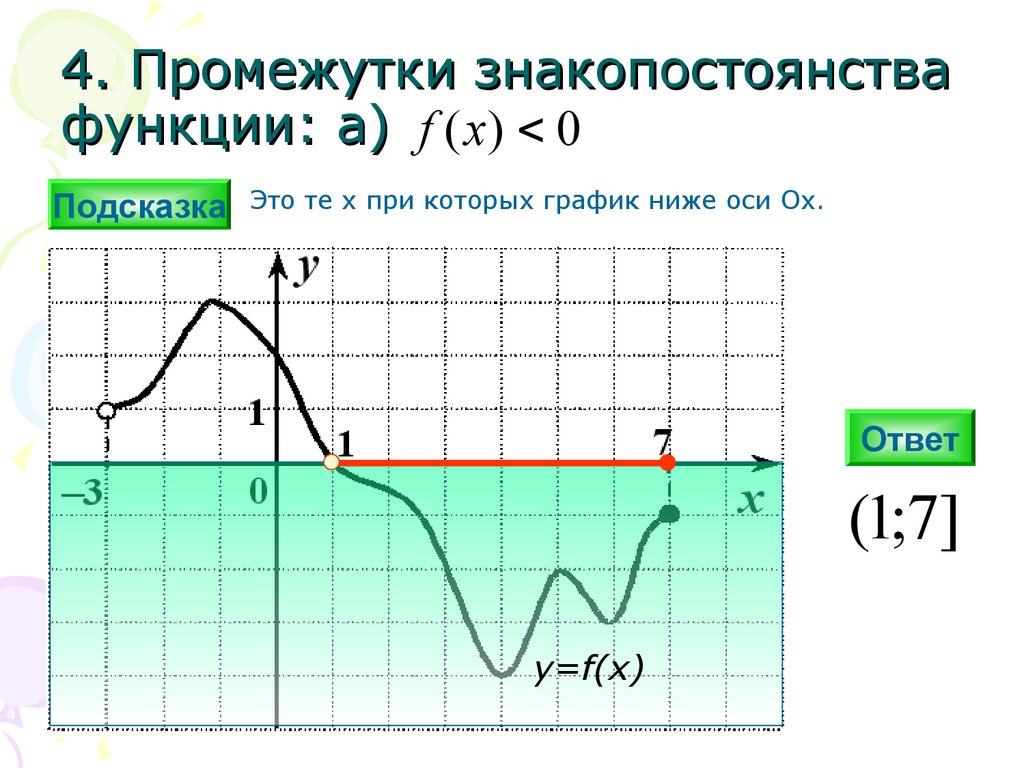
4. Промежутки знакопостоянствафункции: а) f ( x) 0
Подсказка Это те х при которых график ниже оси Ох.
Ответ
(1;7]
y=f(x)
13.
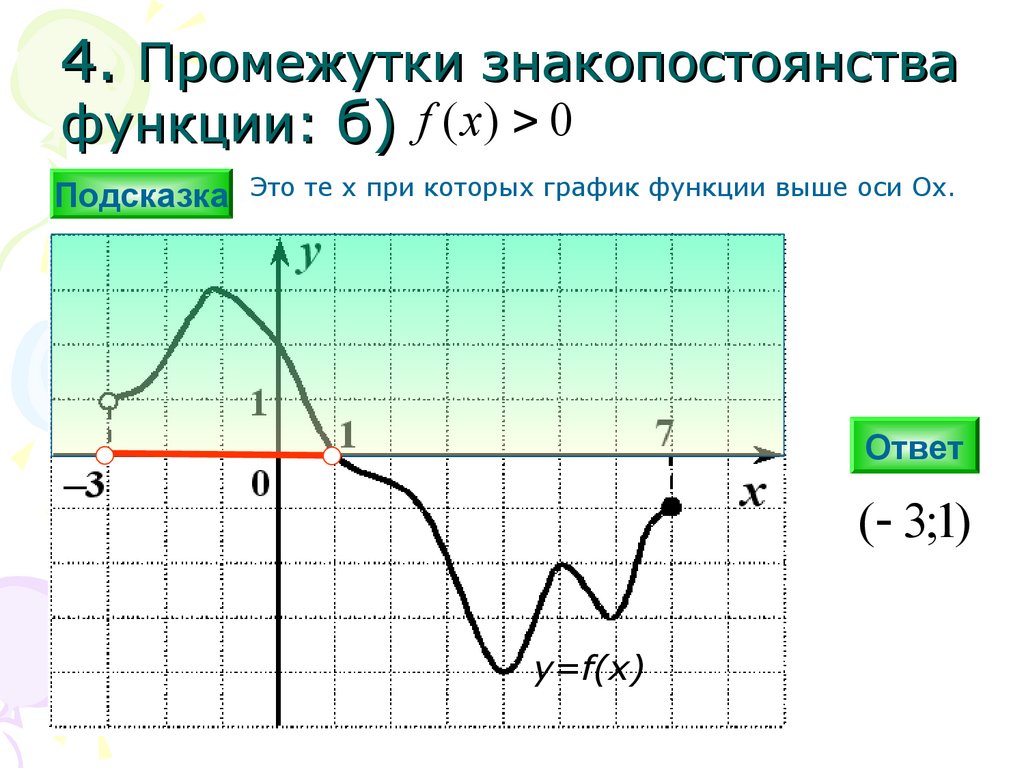
4. Промежутки знакопостоянствафункции: б) f ( x) 0
Подсказка Это те х при которых график функции выше оси Ох.
Ответ
( 3;1)
y=f(x)
14.
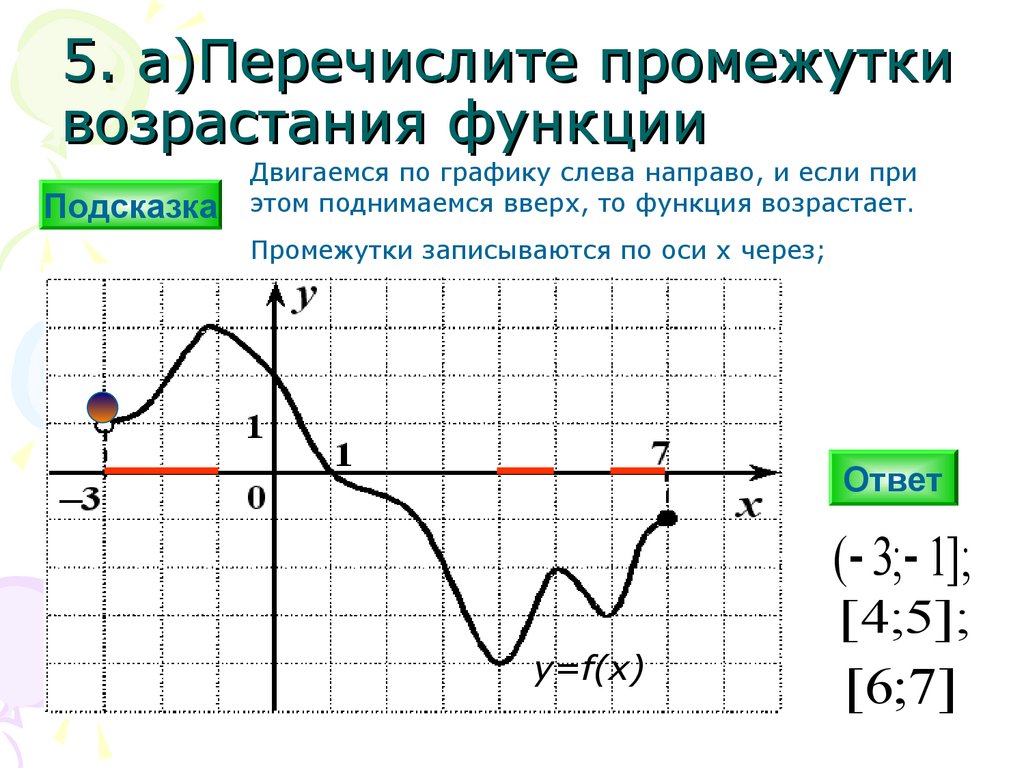
5. а)Перечислите промежуткивозрастания функции
Подсказка
Двигаемся по графику слева направо, и если при
этом поднимаемся вверх, то функция возрастает.
Промежутки записываются по оси х через;
Ответ
( 3; 1];
y=f(x)
[ 4;5];
[6;7]
15.
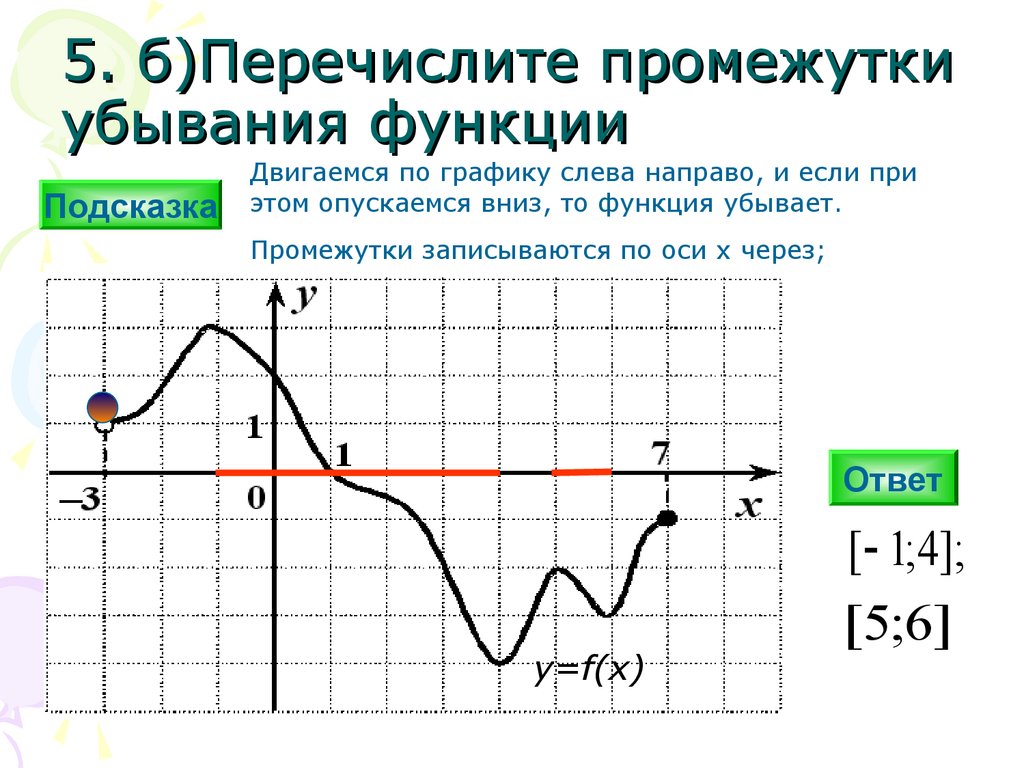
5. б)Перечислите промежуткиубывания функции
Подсказка
Двигаемся по графику слева направо, и если при
этом опускаемся вниз, то функция убывает.
Промежутки записываются по оси х через;
Ответ
y=f(x)
[ 1;4];
[5;6]
16.
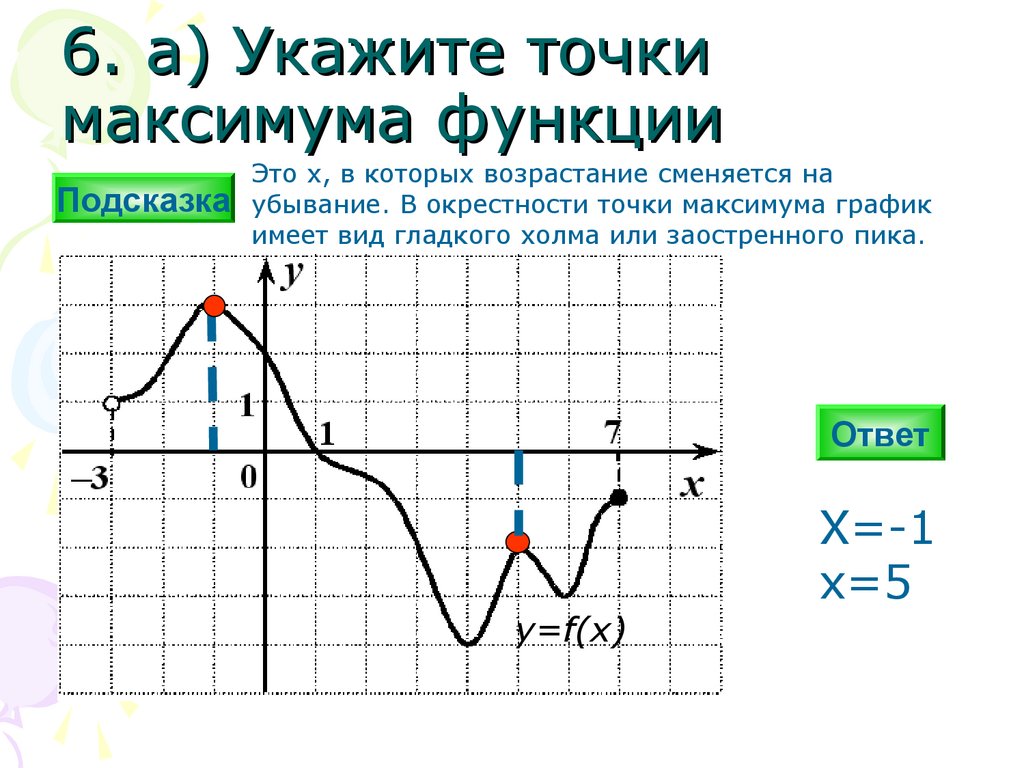
6. а) Укажите точкимаксимума функции
Подсказка
Это х, в которых возрастание сменяется на
убывание. В окрестности точки максимума график
имеет вид гладкого холма или заостренного пика.
Ответ
y=f(x)
X=-1
x=5
17.
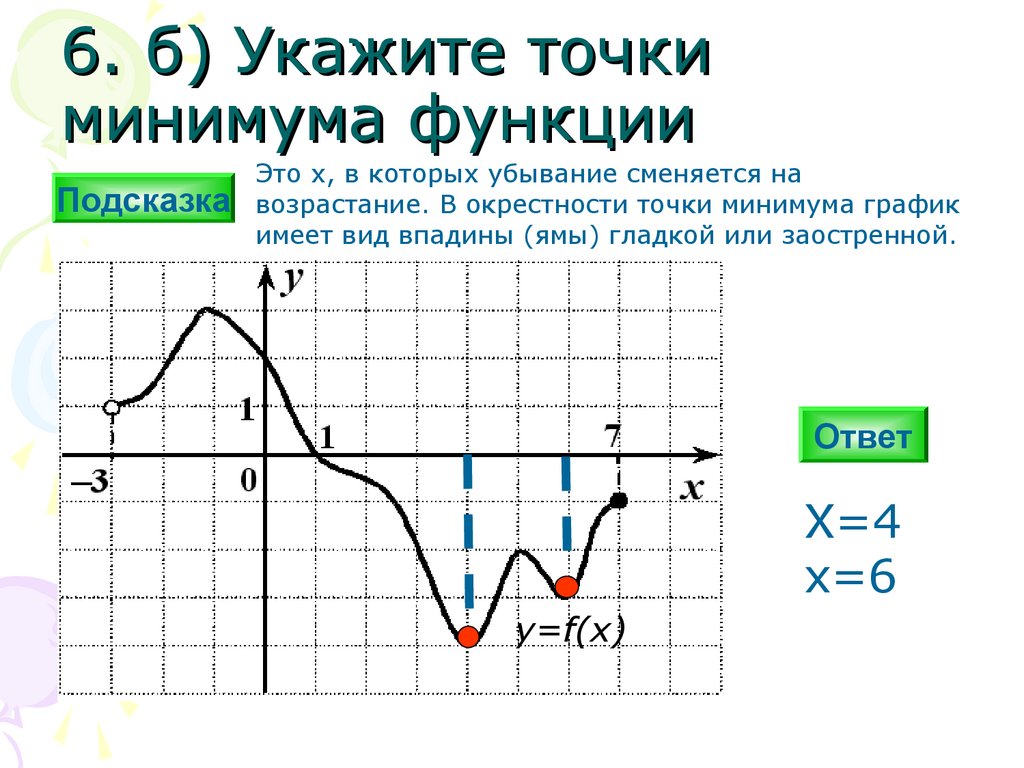
6. б) Укажите точкиминимума функции
Подсказка
Это х, в которых убывание сменяется на
возрастание. В окрестности точки минимума график
имеет вид впадины (ямы) гладкой или заостренной.
Ответ
X=4
x=6
y=f(x)
18.
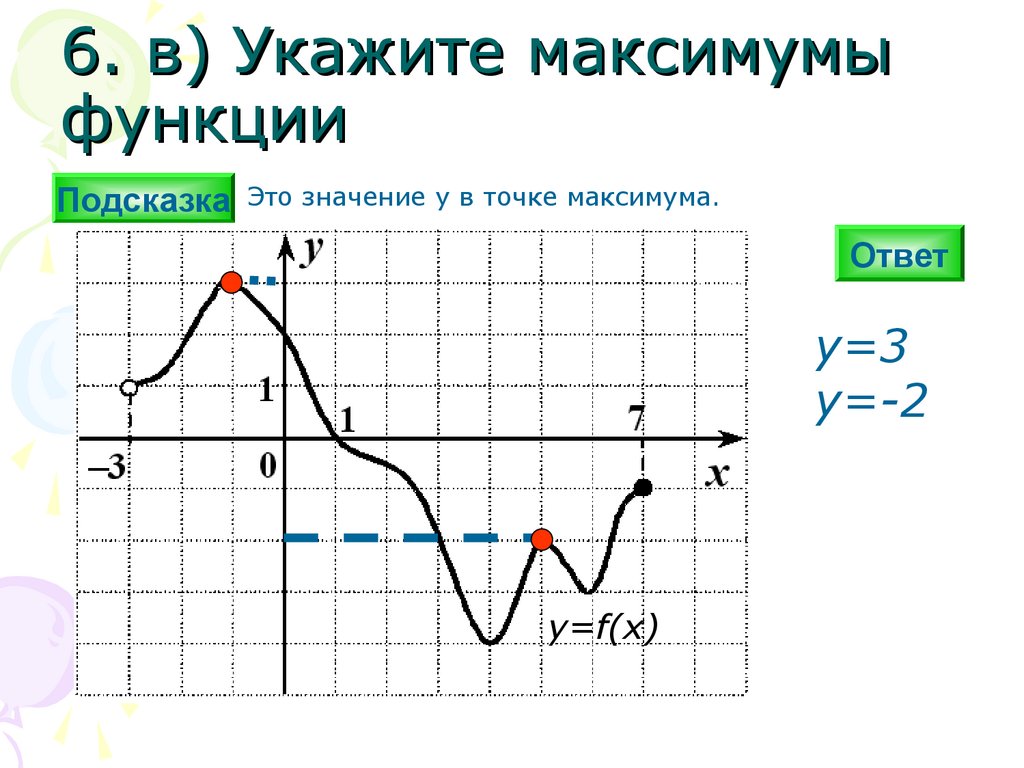
6. в) Укажите максимумыфункции
Подсказка Это значение y в точке максимума.
Ответ
y=3
y=-2
y=f(x)
19.
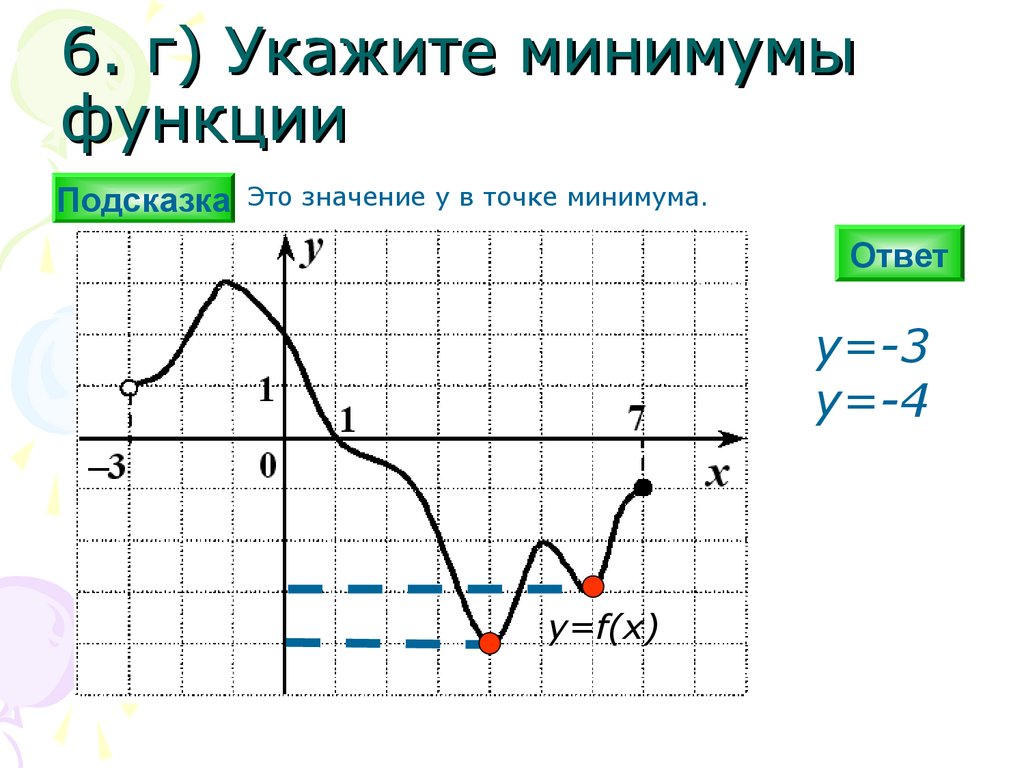
6. г) Укажите минимумыфункции
Подсказка Это значение y в точке минимума.
Ответ
y=-3
y=-4
y=f(x)
20.
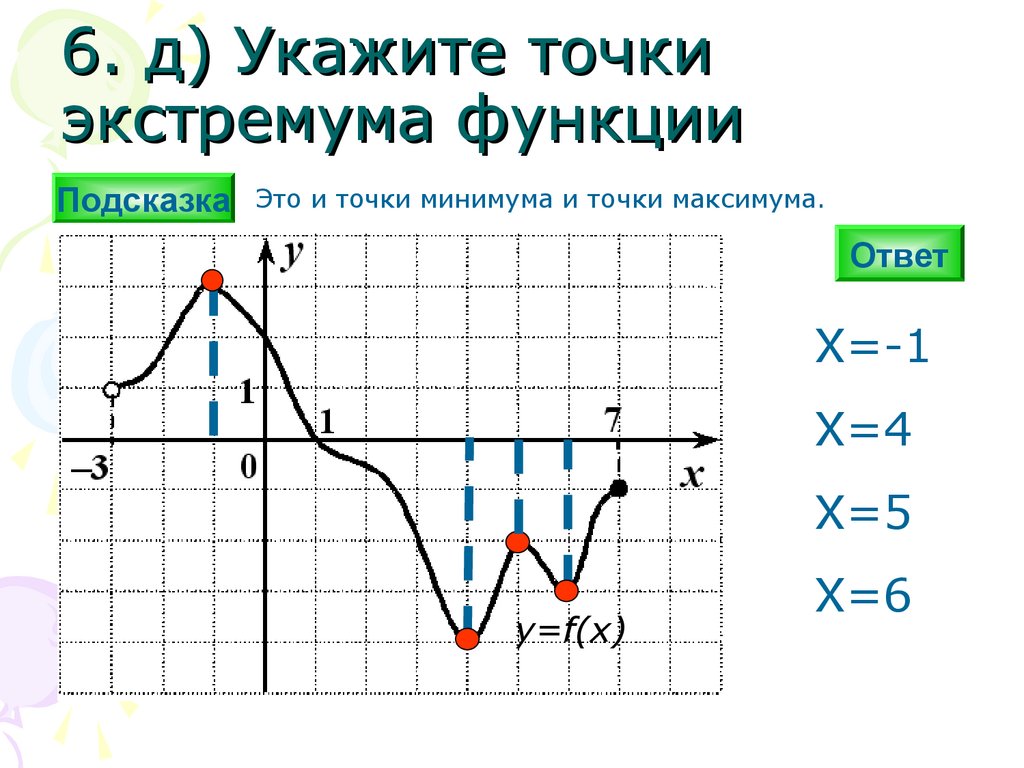
6. д) Укажите точкиэкстремума функции
Подсказка
Это и точки минимума и точки максимума.
Ответ
X=-1
Х=4
Х=5
y=f(x)
Х=6
21.
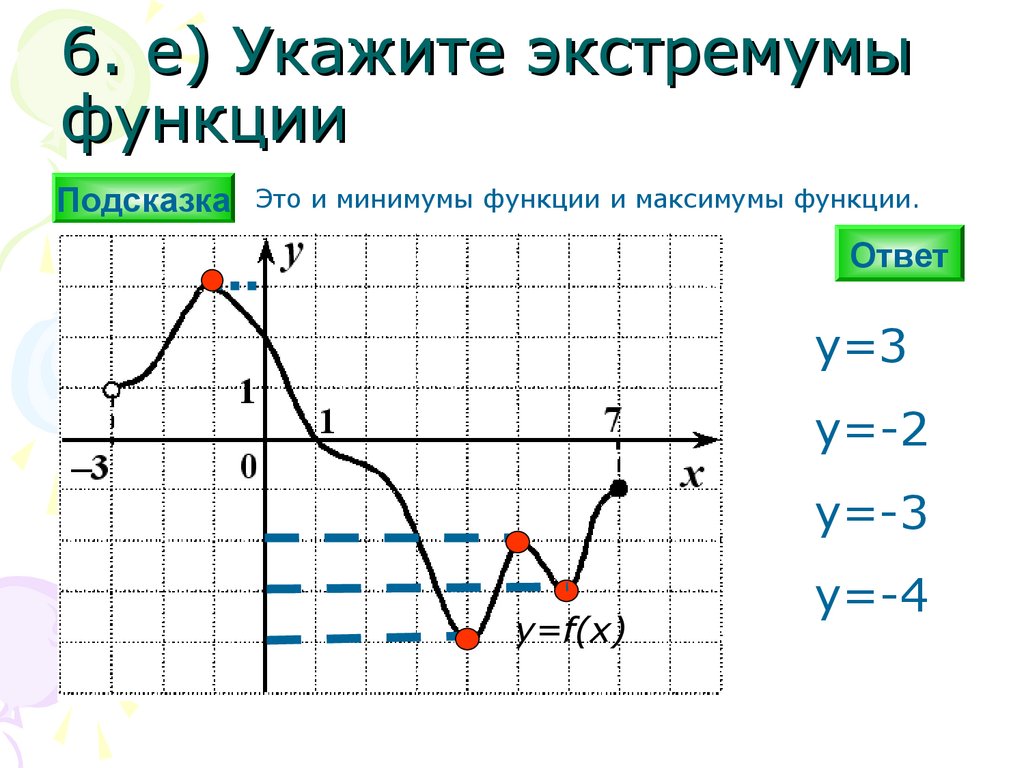
6. е) Укажите экстремумыфункции
Подсказка
Это и минимумы функции и максимумы функции.
Ответ
y=3
y=-2
y=-3
y=f(x)
y=-4
22.
1)2)
3)
4)
5)
6)
7)
Схема исследования
функций:
Найти области определения и значений данной
функции.
Выяснить обладает ли функция особенностями,
облегчающими исследование (четность,
периодичность).
Координаты точек пересечения с осями
координат.
Промежутки знакопостоянства функци. (Т.е.те х
при которых y>0 и y<0).
Промежутки возрастания и убывания.
Найти точки экстремума, вид экстремума и
экстремумы функции.
Исследовать поведение функции в окрестности
характерных точек, не входящих в область
определения и при больших (по модулю)
значениях аргумента).
23.
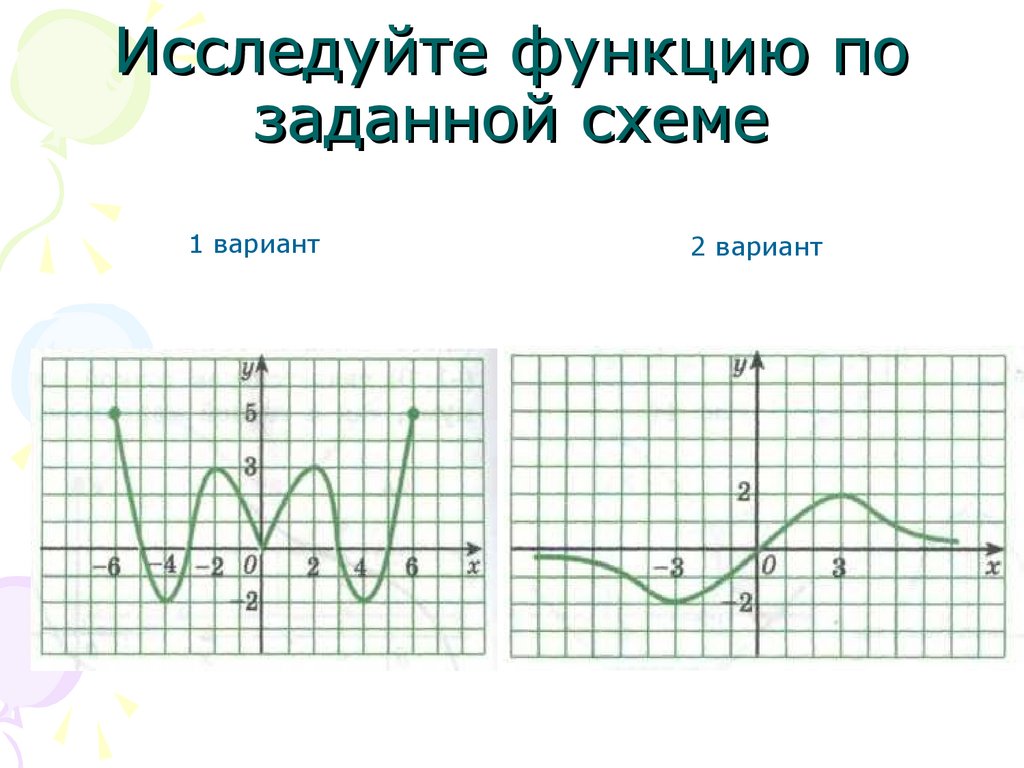
Исследуйте функцию позаданной схеме
1 вариант
2 вариант
24.
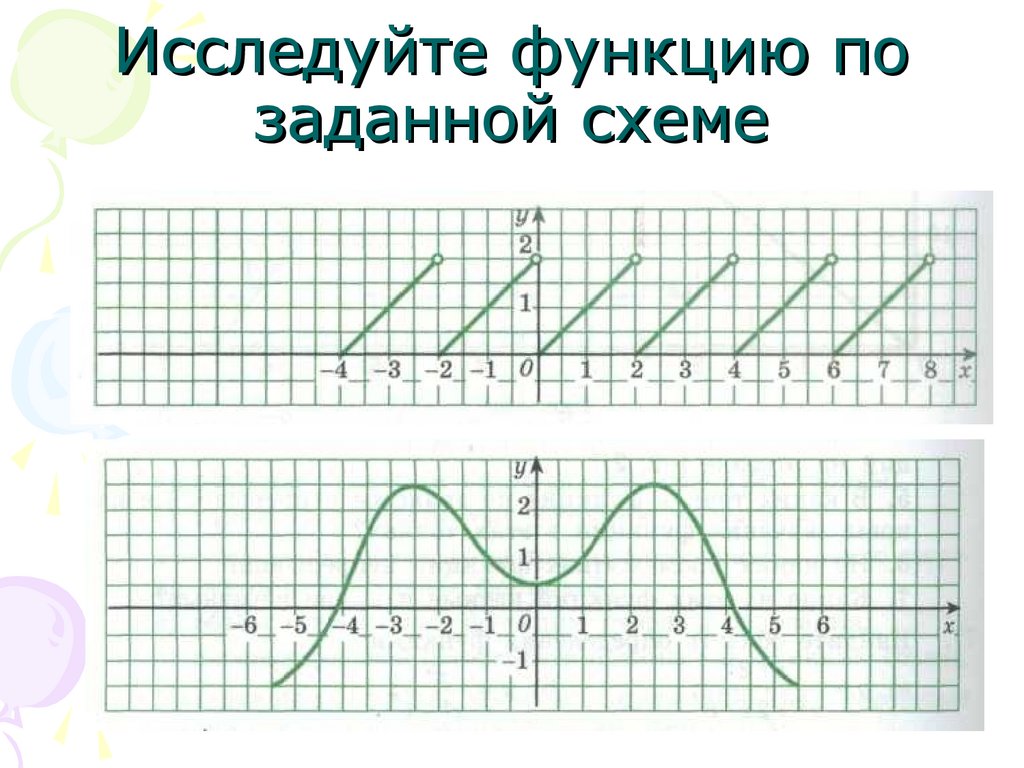
Исследуйте функцию позаданной схеме
25.
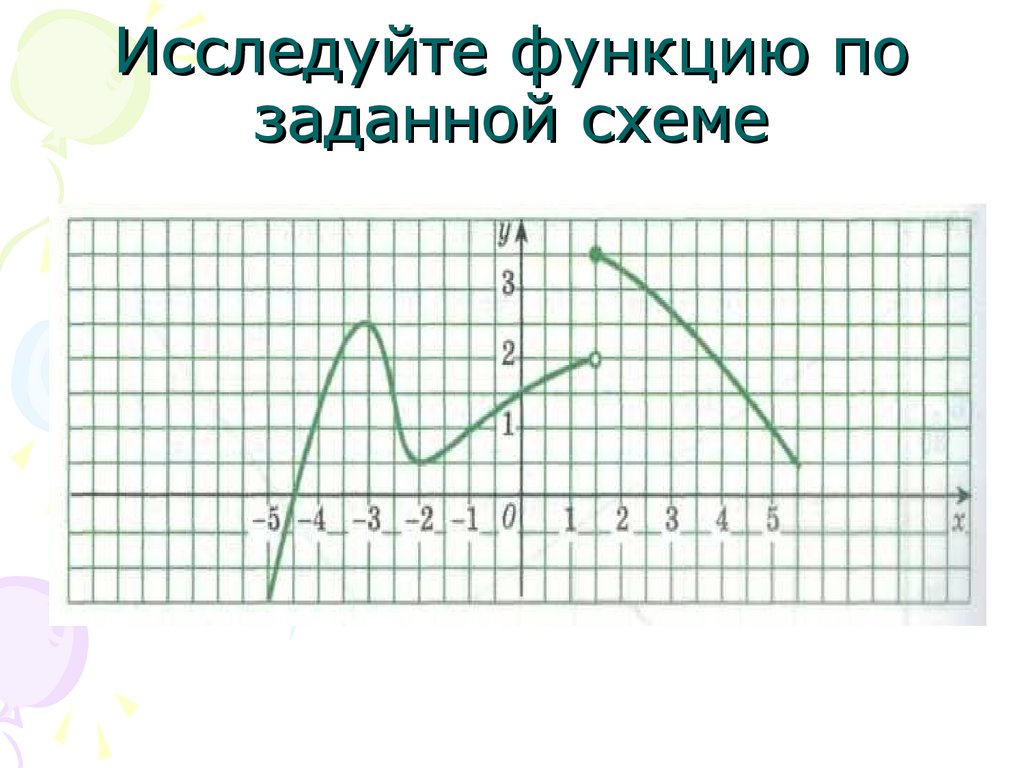
Исследуйте функцию позаданной схеме
26.
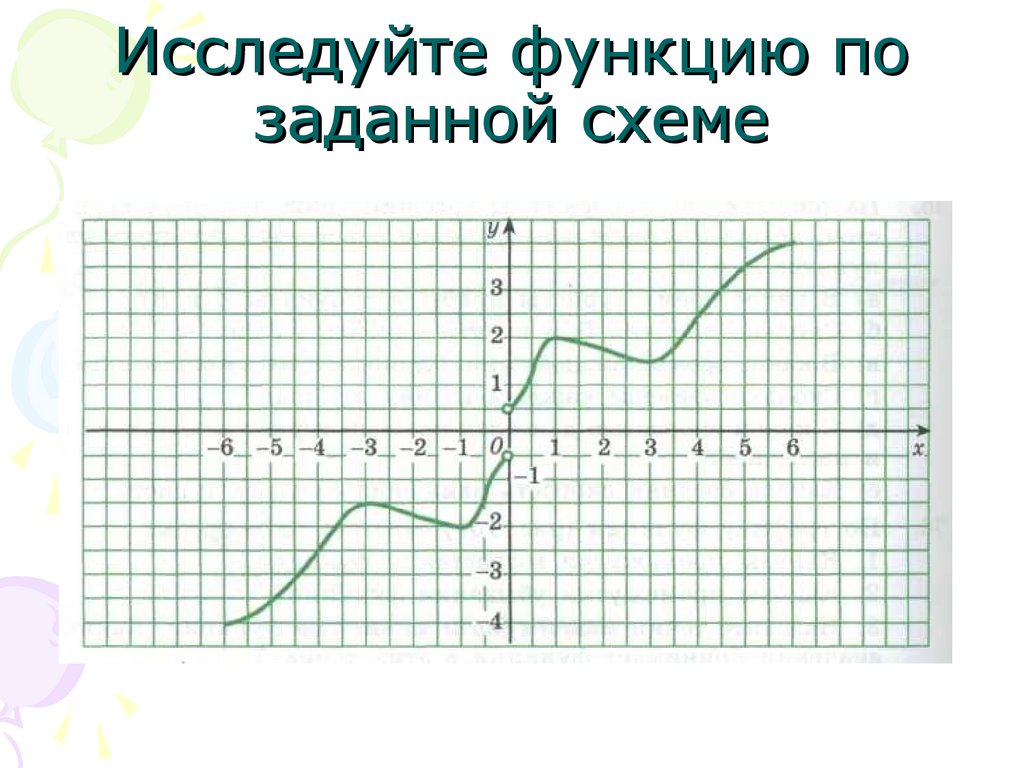
Исследуйте функцию позаданной схеме



 mathematics
mathematics