Математика. Раздел 7. Функции и графики. Занятие 70. Схема исследования функции

1.

Математика
Раздел 7. Функции и графики
Занятие 70.
Схема исследования функции

2.

Свойства функций
1. Область определения D(f)
2. Область значений Е(f)
3. Нули функции
4. Промежутки знакопостоянства
5. Промежутки монотонности
6. Экстремумы
7. Четность/нечетность
8. Периодичность (если есть)
9. Уравнения асимптот (если есть)

3.

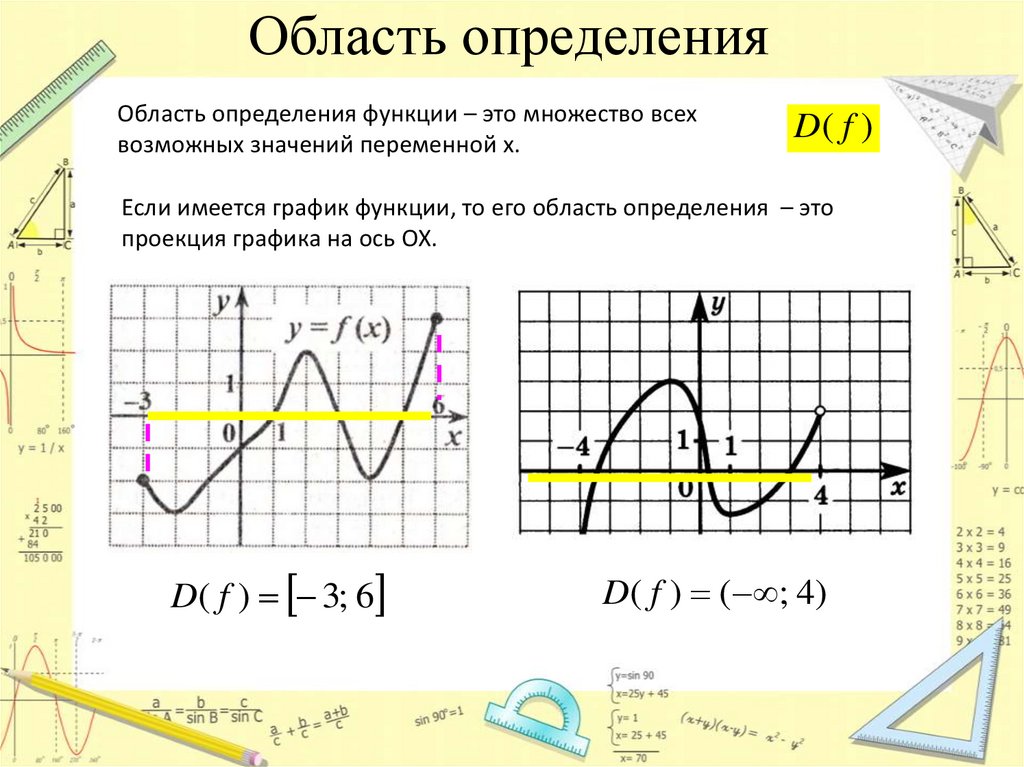
Область определения
Область определения функции – это множество всех
возможных значений переменной х.
D( f )
Если имеется график функции, то его область определения – это
проекция графика на ось ОХ.
D( f ) 3; 6
D ( f ) ( ; 4)

4.

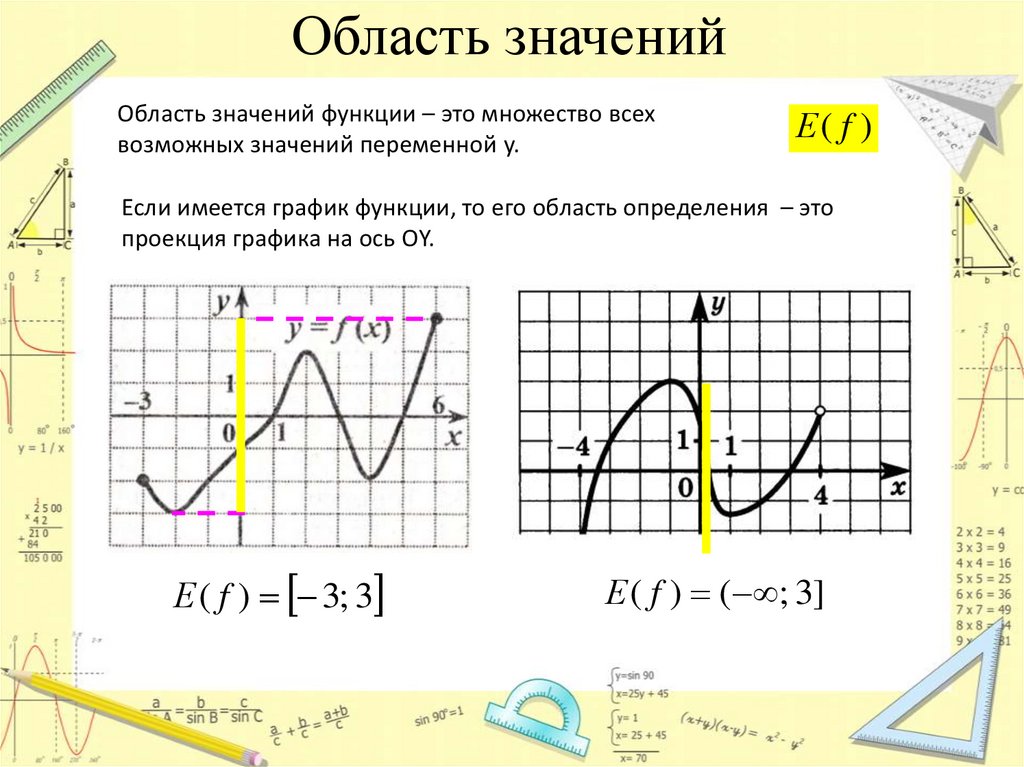
Область значений
Область значений функции – это множество всех
возможных значений переменной y.
Е( f )
Если имеется график функции, то его область определения – это
проекция графика на ось ОY.
Е ( f ) 3; 3
Е ( f ) ( ; 3]

5.

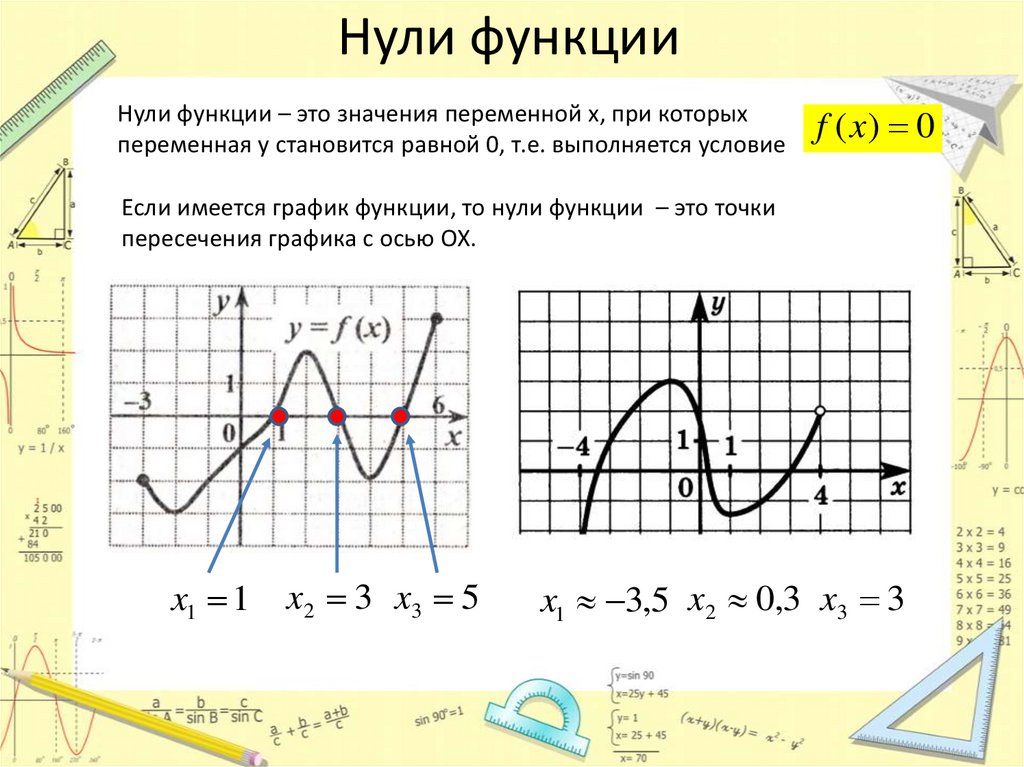
Нули функции
Нули функции – это значения переменной х, при которых
переменная y становится равной 0, т.е. выполняется условие
f ( x) 0
Если имеется график функции, то нули функции – это точки
пересечения графика с осью ОХ.
x1 1
x2 3 x3 5
x1 3,5 x2 0,3 x3 3

6.

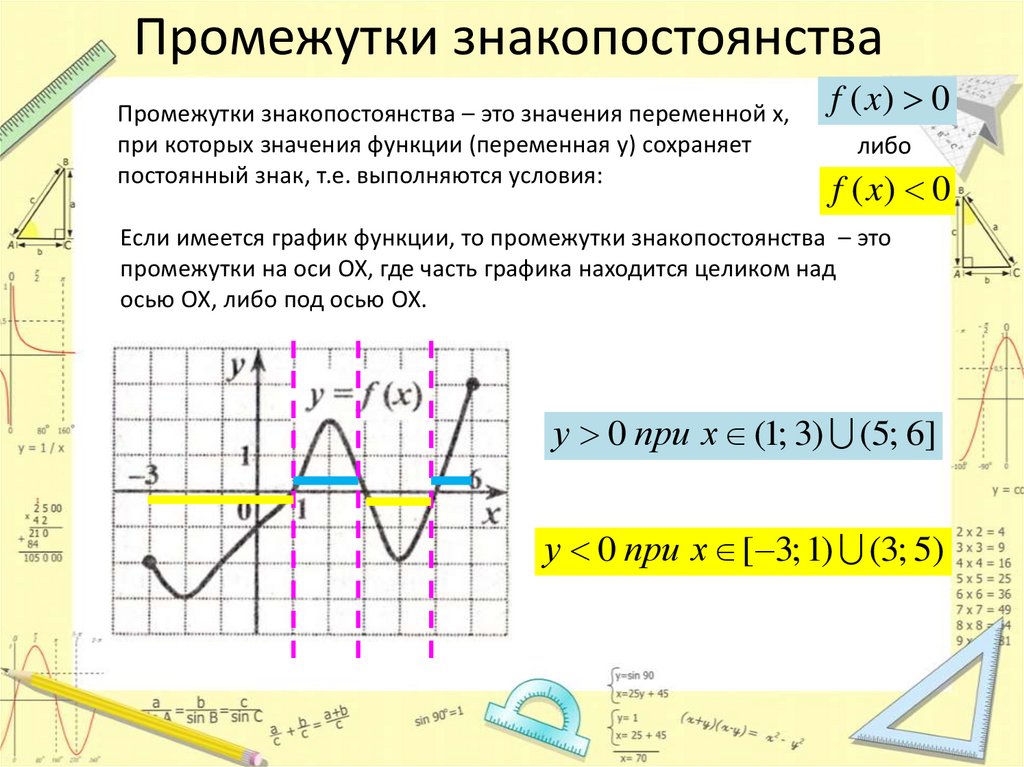
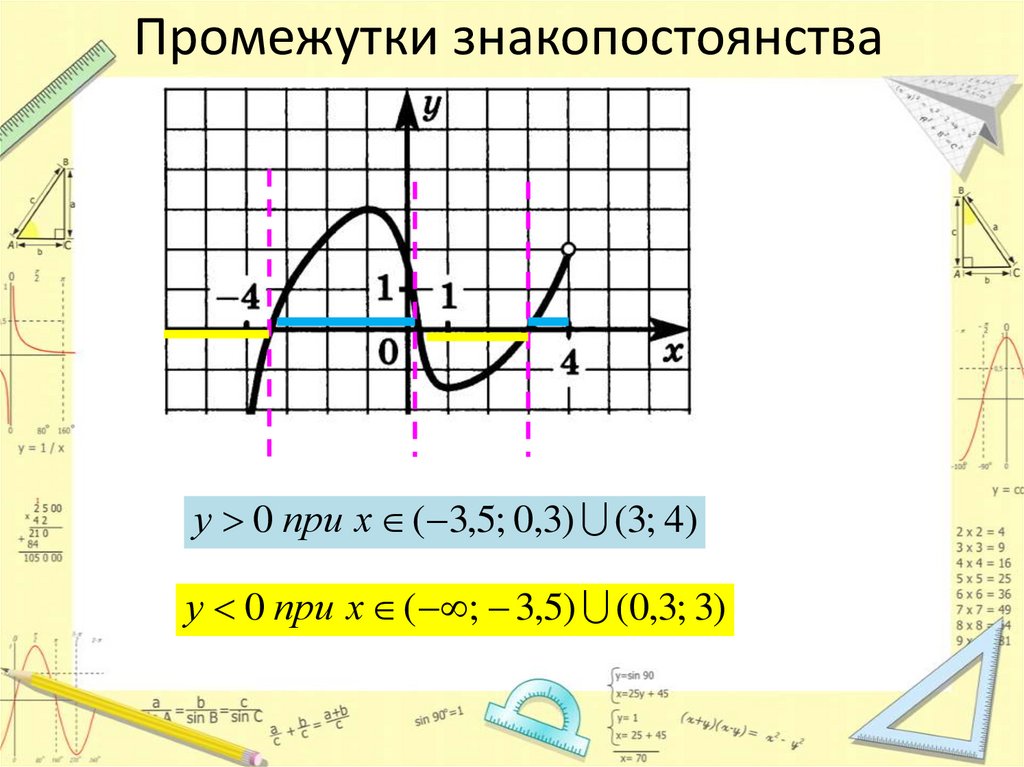
Промежутки знакопостоянства
Промежутки знакопостоянства – это значения переменной х,
при которых значения функции (переменная y) сохраняет
постоянный знак, т.е. выполняются условия:
f ( x) 0
либо
f ( x) 0
Если имеется график функции, то промежутки знакопостоянства – это
промежутки на оси ОХ, где часть графика находится целиком над
осью ОХ, либо под осью ОХ.
у 0 при х (1; 3) (5; 6]
у 0 при х [ 3; 1) (3; 5)

7.

Промежутки знакопостоянства
у 0 при х ( 3,5; 0,3) (3; 4)
у 0 при х ( ; 3,5) (0,3; 3)

8.

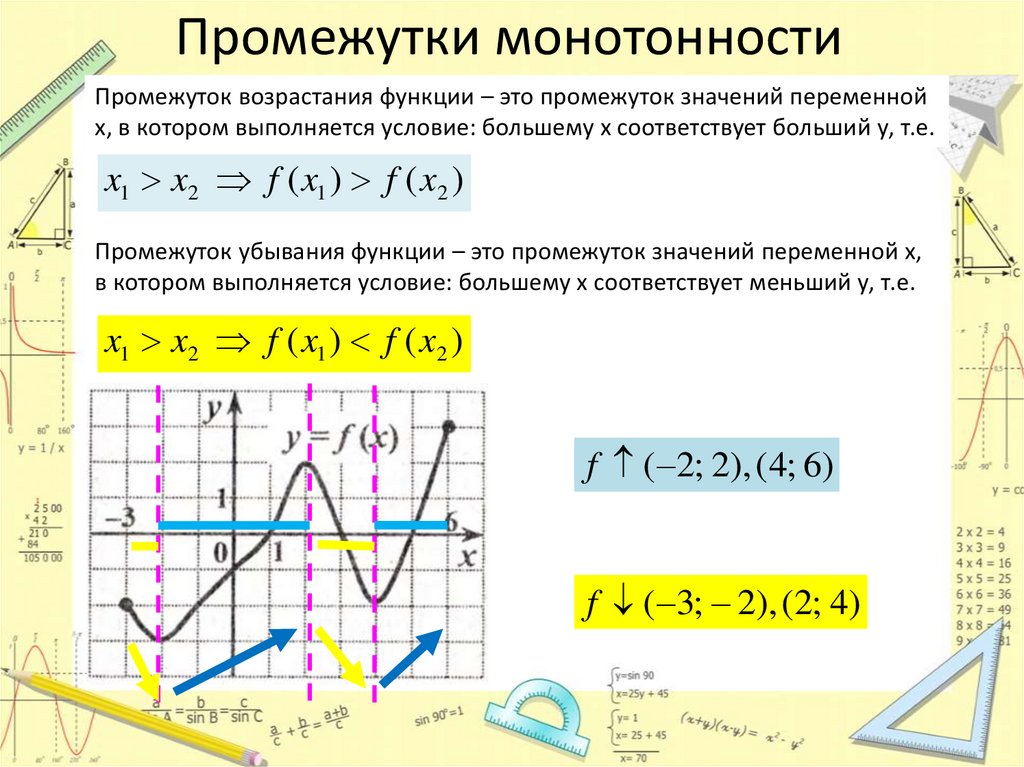
Промежутки монотонности
Промежуток возрастания функции – это промежуток значений переменной
х, в котором выполняется условие: большему х соответствует больший у, т.е.
x1 x2 f ( x1 ) f ( x2 )
Промежуток убывания функции – это промежуток значений переменной х,
в котором выполняется условие: большему х соответствует меньший у, т.е.
x1 x2 f ( x1 ) f ( x2 )
f ( 2; 2), (4; 6)
f ( 3; 2), (2; 4)

9.

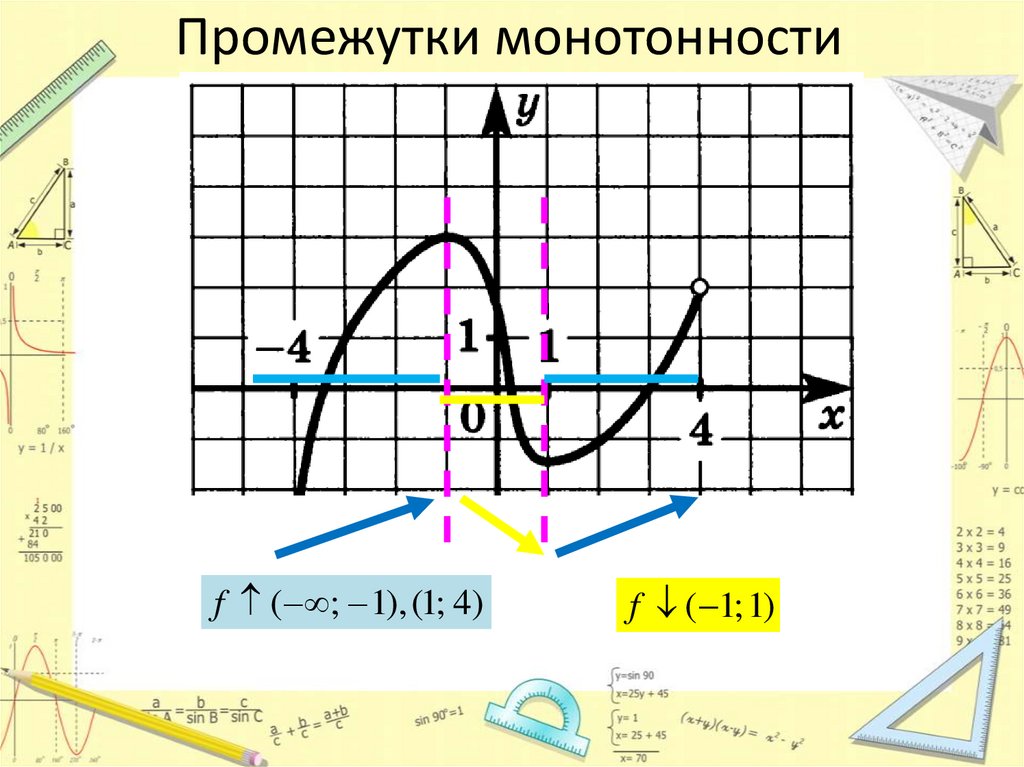
Промежутки монотонности
f ( ; 1), (1; 4)
f ( 1; 1)

10.

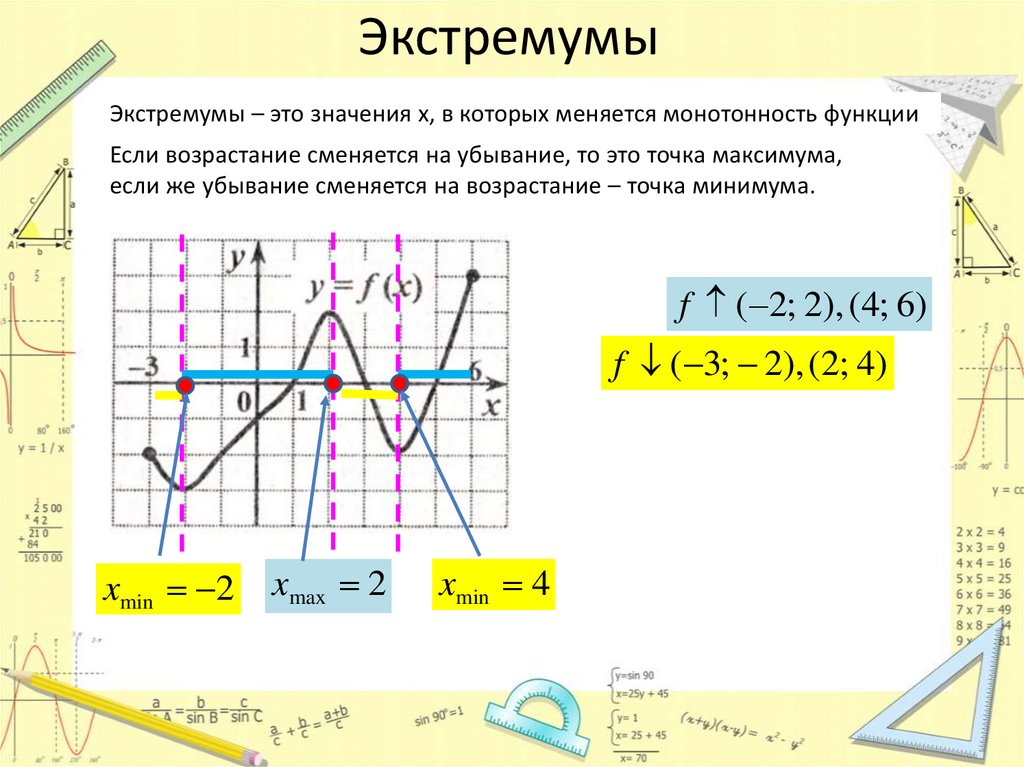
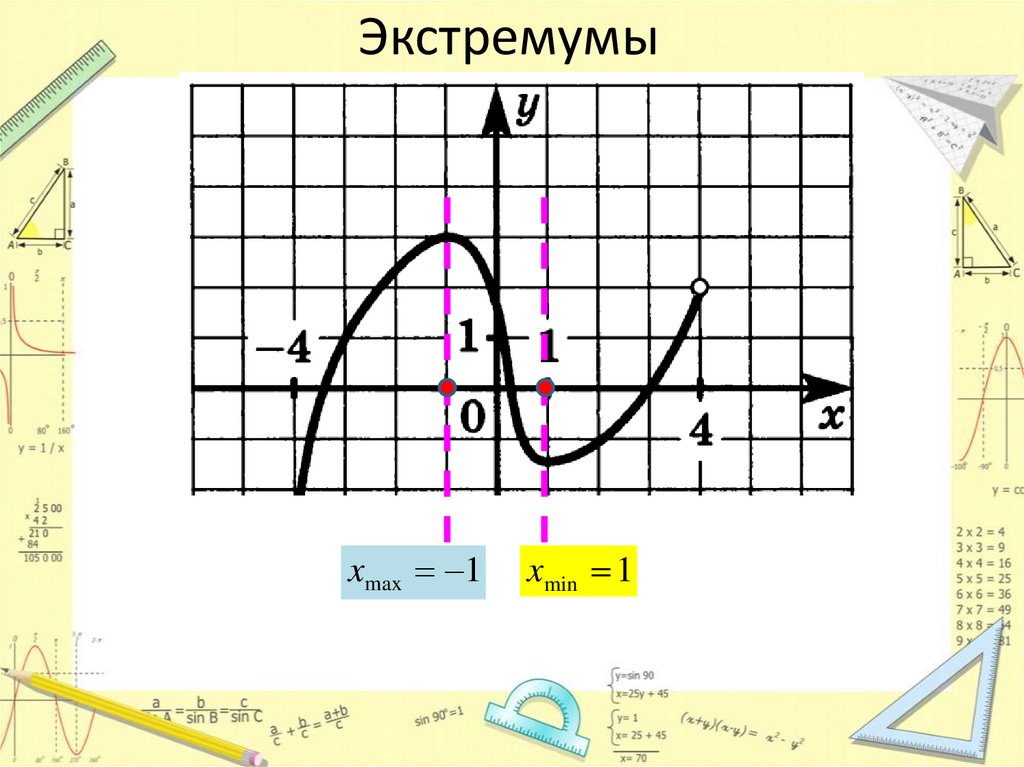
Экстремумы
Экстремумы – это значения х, в которых меняется монотонность функции
Если возрастание сменяется на убывание, то это точка максимума,
если же убывание сменяется на возрастание – точка минимума.
f ( 2; 2), (4; 6)
f ( 3; 2), (2; 4)
xmin 2
xmax 2
xmin 4

11.

Экстремумы
xmax 1
xmin 1

12.

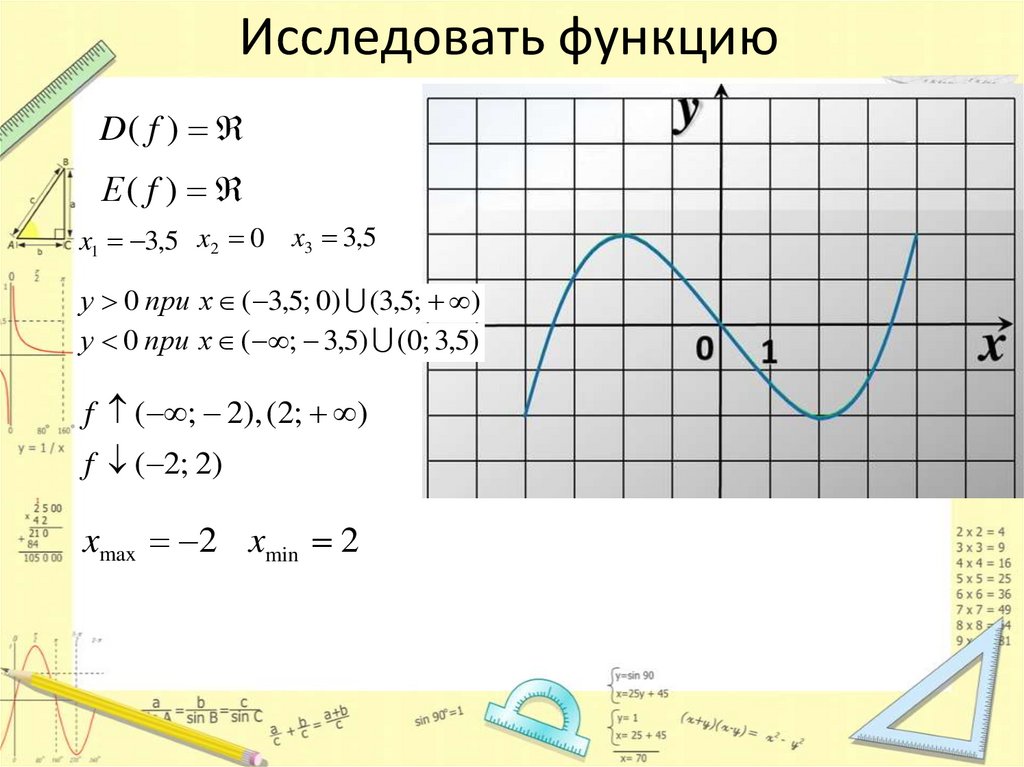
Исследовать функцию
D( f )
Е( f )
x1 3,5 x2 0 x3 3,5
у 0 при х ( 3,5; 0) (3,5; )
у 0 при х ( ; 3,5) (0; 3,5)
f ( ; 2), (2; )
f ( 2; 2)
xmax 2 xmin 2

13.

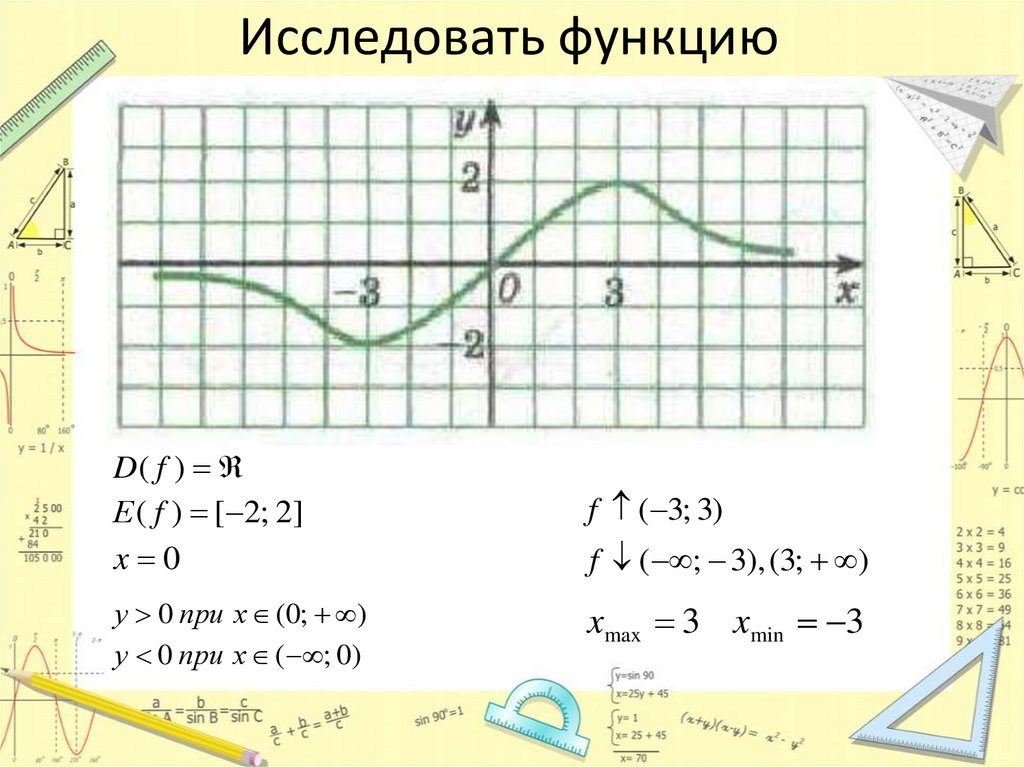
Исследовать функцию
D( f )
Е ( f ) [ 2; 2]
x 0
f ( 3; 3)
у 0 при х (0; )
у 0 при х ( ; 0)
xmax 3 xmin 3
f ( ; 3), (3; )

14.

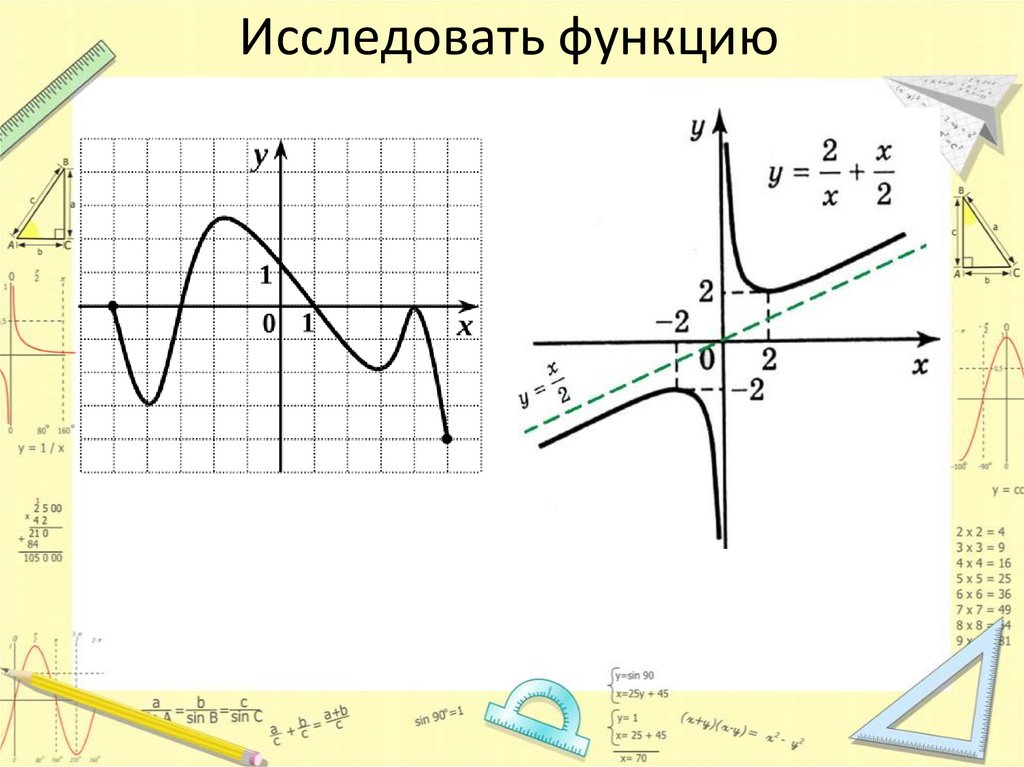
Исследовать функцию

15.

Шмельков Владимир Юрьевич
преподаватель математики
ГБПОУ ЗКНО
Москва, 2021г.