Similar presentations:
Основные свойства функций и их графики
1. Основные свойства функций и их графики
2. Функция. Область определения. Область значений
Пусть X и Y— два множества.Функция у=f(х) — это правило или закон
f, по которому каждому числу x X
ставится
в
соответствие
единственное число y Y .
3.
Если элементами множеств Х и Уявляются действительные числа, т. е.
x , y , то функцию
f
называют
числовой функцией.
Переменная x называется при этом
аргументом или независимой переменной, а y – функцией или зависимой
переменной. Относительно величин x и
y
говорят, что они находятся в
функциональной зависимости.
f (c) – частное значение функции f при x c
4.
Область определения функции f(х)(D(f(х)) – множество X, т.е. всевозможные
значения независимой переменной х.
Область значений функции f(х) (E(f(х)) –
множество, состоящее из всевозможных
чисел f(х) при x X .
5. Пример
1)f ( x) 2 x
Область определения D( f ) [0; ) .
Область значений E ( f ) [2; ) .
2) y 5
x 3
Область определения D( y ) ; 3 (3; ).
Область значений E ( y) ; 0 (0; ) .
6. График функции
Графиком функции y y( x), x X R.является множество всех точек x, y
плоскости Oxy , для каждой из которых
значение аргумента x является абсциссой, а
значение функции y - ординатой.
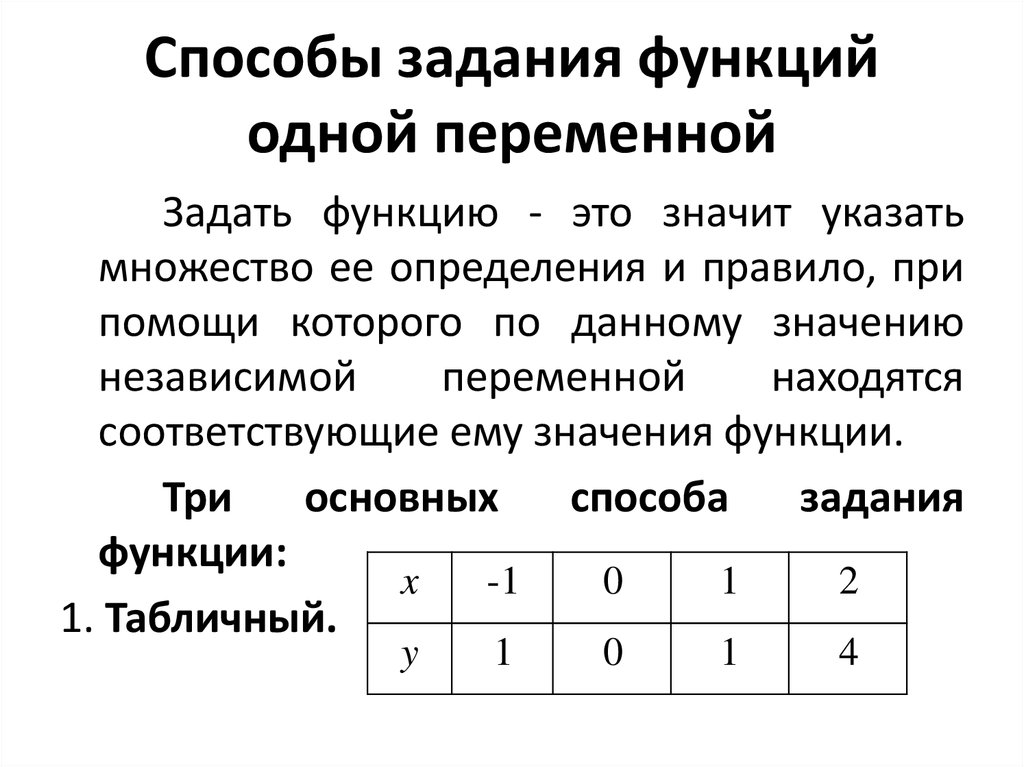
7. Способы задания функций одной переменной
Задать функцию - это значит указатьмножество ее определения и правило, при
помощи которого по данному значению
независимой
переменной
находятся
соответствующие ему значения функции.
Три
основных
способа
задания
функции:
x
-1
0
1
2
1. Табличный.
y
1
0
1
4
8.
2. Графический.y
y
M x, y
x
0
X
x
9.
3. аналитический, который имеет триразновидности:
А) явный способ задания - с помощью одного
или нескольких аналитических выражений y y( x), x X R. . Например,
y 1 x2
x X 0, 1 ;
Б) неявный, т.е. с помощью уравнения
F ( x, y) 0, x X , y Y
В) параметрический.
10. Свойства функций
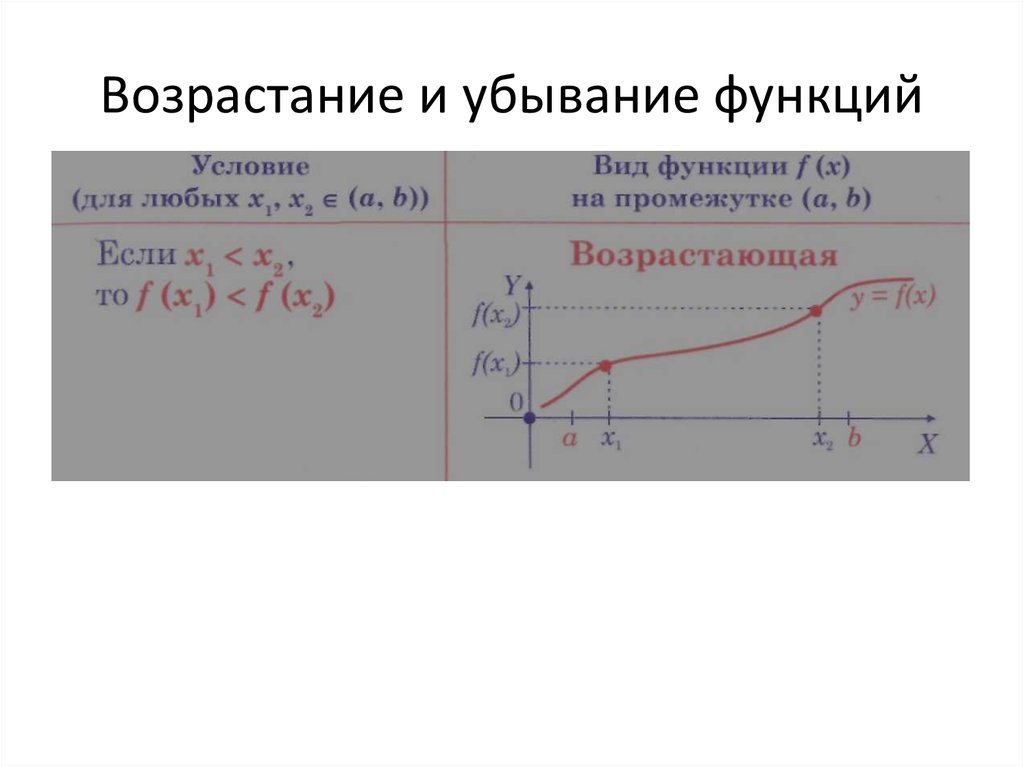
11. Возрастание и убывание функций
12.
13.
Монотонные функции — возрастающие,убывающие,
неубывающие
и
невозрастающие.
Промежутки монотонности функции f(х) –
непересекающиеся промежутки из D( f ) , на
каждом из которых функция f(х) монотонна.
14. Четность и нечетность функции
15. Пример
1) f ( x) x 2 1 - четнаяD( f ) R
f ( x) ( x) 2 1 x 2 1 f ( x)
2)
f ( x) x 3
- нечетная
D( f ) R
f ( x) ( x) 3 x 3 f ( x)
16. Периодичность функций
Функция f(х) периодическая — существуеттакое числоT 0 (период), что:
1) Если x D( f ) , то ( x T ) D( f ) ;
2) f ( x T ) f ( x) .
Если Т – период f(х), то любое число nT – тоже
период f(х). Основной период — наименьший
из положительных периодов.
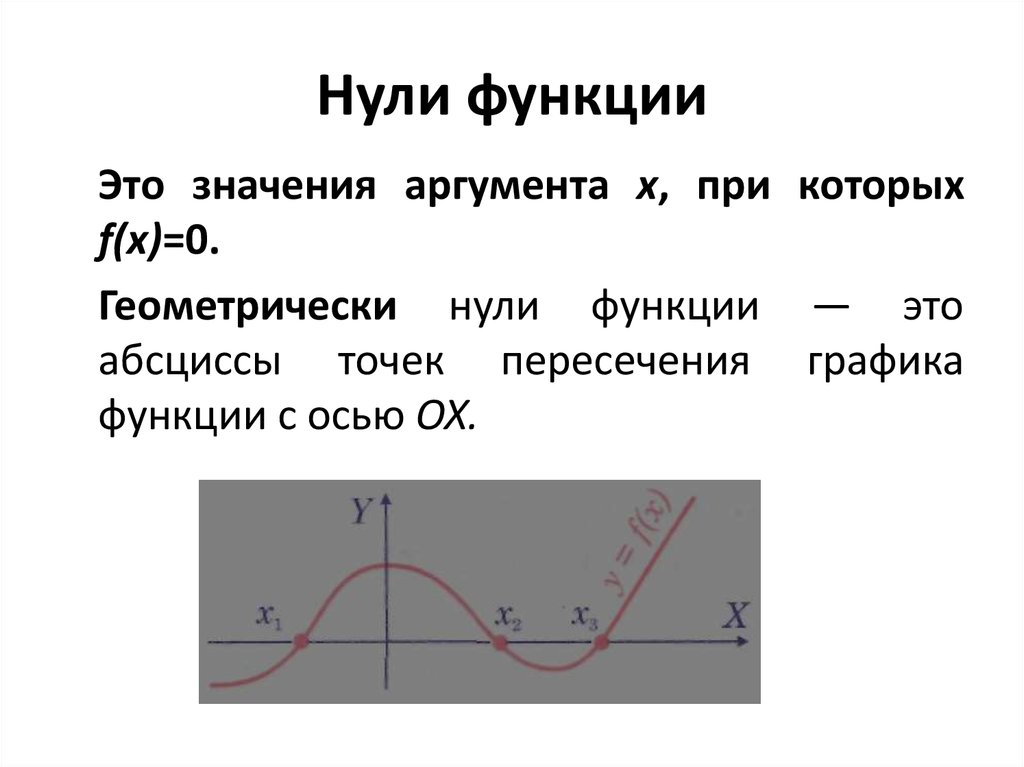
17. Нули функции
Это значения аргумента x, при которыхf(х)=0.
Геометрически нули функции — это
абсциссы точек пересечения графика
функции с осью ОХ.
18. Промежутки знакопостоянства
Промежутки знакопостоянства f(х) –промежутки из D( f ) , на которых либо f ( x) 0 ,
либо f ( x) 0 .
Нули функции f(х) разбивают D( f )
промежутки знакопостоянства.
на
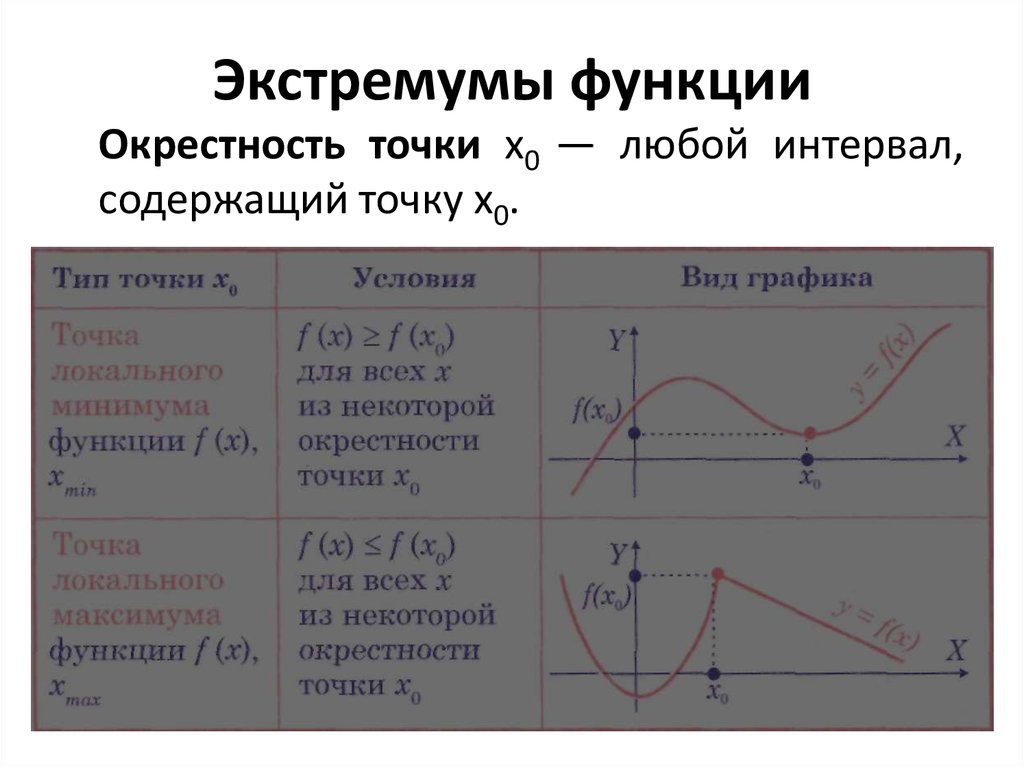
19. Экстремумы функции
Окрестность точки х0 — любой интервал,содержащий точку х0.
20.
Точки экстремума — точки минимума имаксимума.
Минимум f(х) — значение f(xmin).
Максимум f(х) — значение f(хтах).
Экстремумы f(х) — минимум и максимум
f(х).
Точки экстремума f(х) разбивают D(f) на
промежутки
монотонности
f(x),
т.е.
промежутки возрастания или убывания
функции.
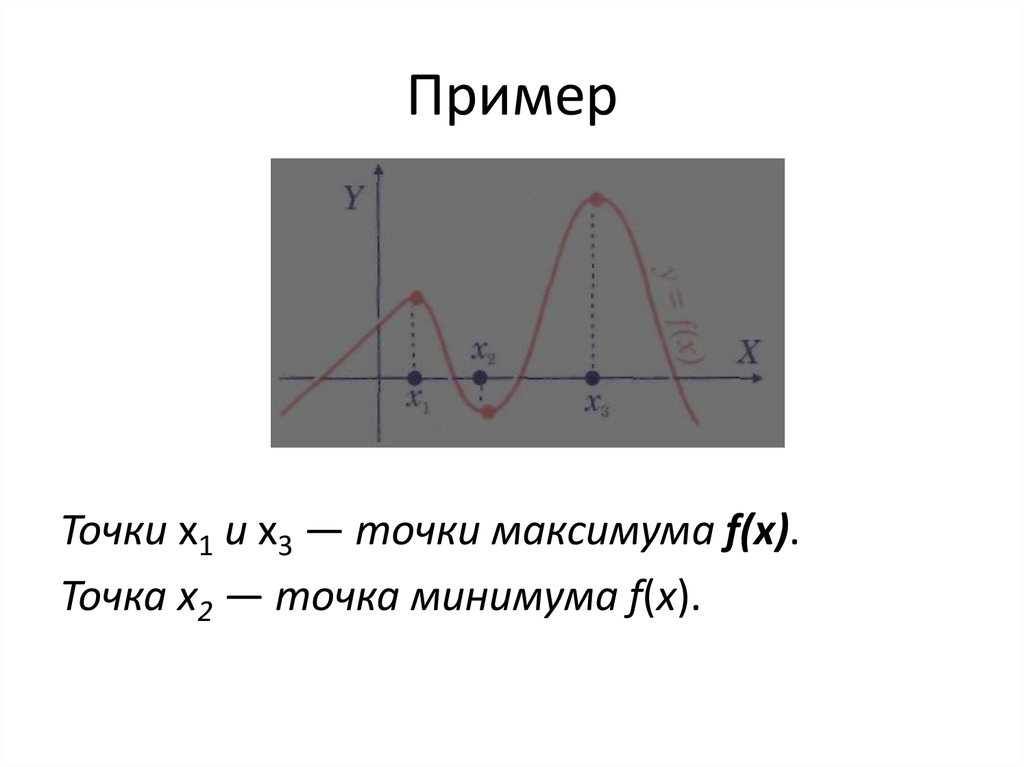
21. Пример
Точки х1 и х3 — точки максимума f(х).Точка х2 — точка минимума f(х).
22. Свойства функций одной переменной
1. Четность и нечетность функции.2. Периодичность функции.
3. Монотонность функции.
4. Ограниченность функции.
23. Основные элементарные функции :
1) Степенная функция y x , x D f , R;2) Показательная функция y a x , a 0, ;
3) Логарифмическая функция
y log a x, a 0, a 1;
4) Тригонометрические функции
y sin x, y cos x, y tg x, y ctg x, x D f
5) Обратные тригонометрические функции
y arcsin x, y arccos x, y arctg x, y arcctg x.
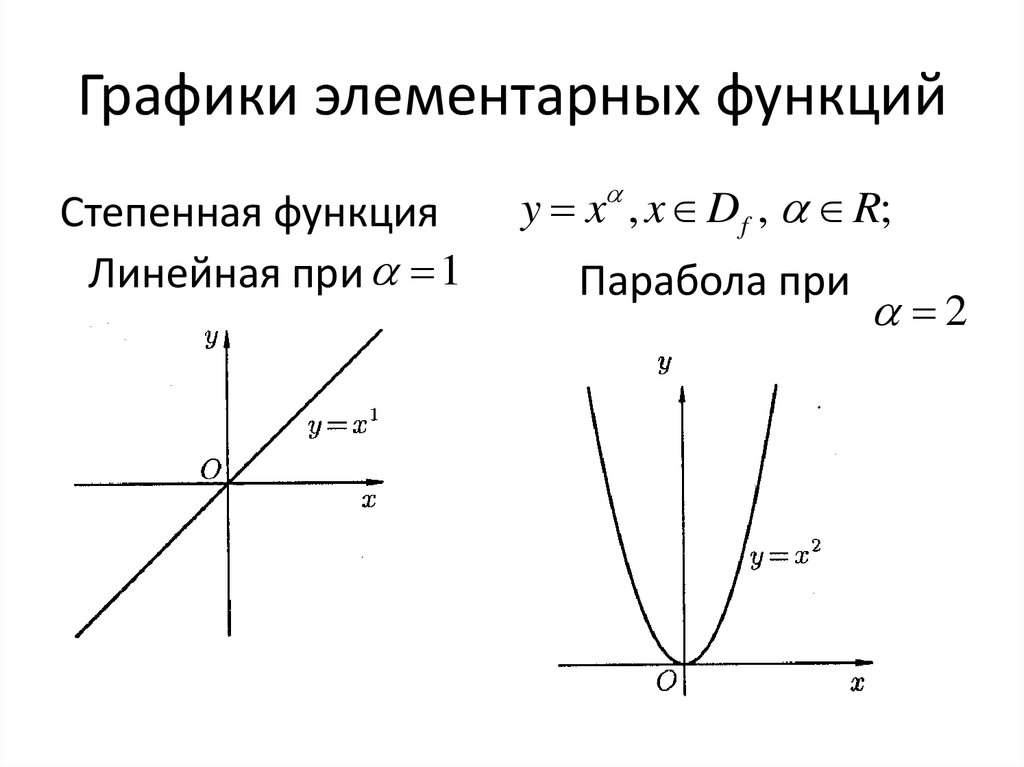
24. Графики элементарных функций
Степенная функцияЛинейная при 1
y x , x D f , R;
Парабола при
2
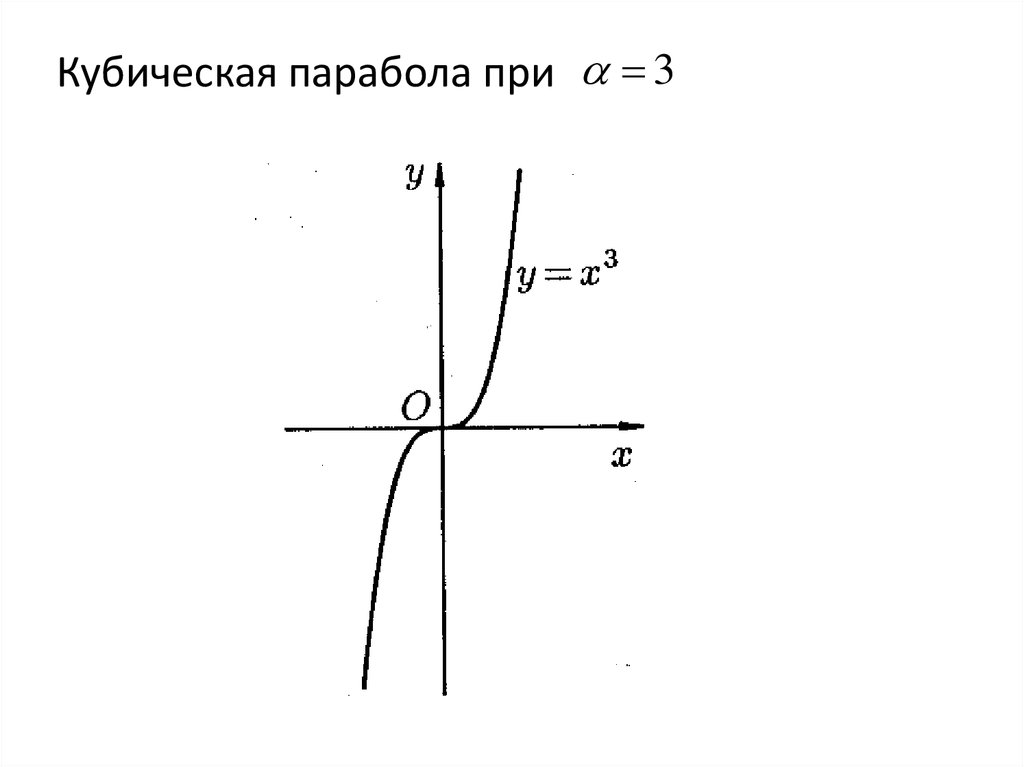
25.
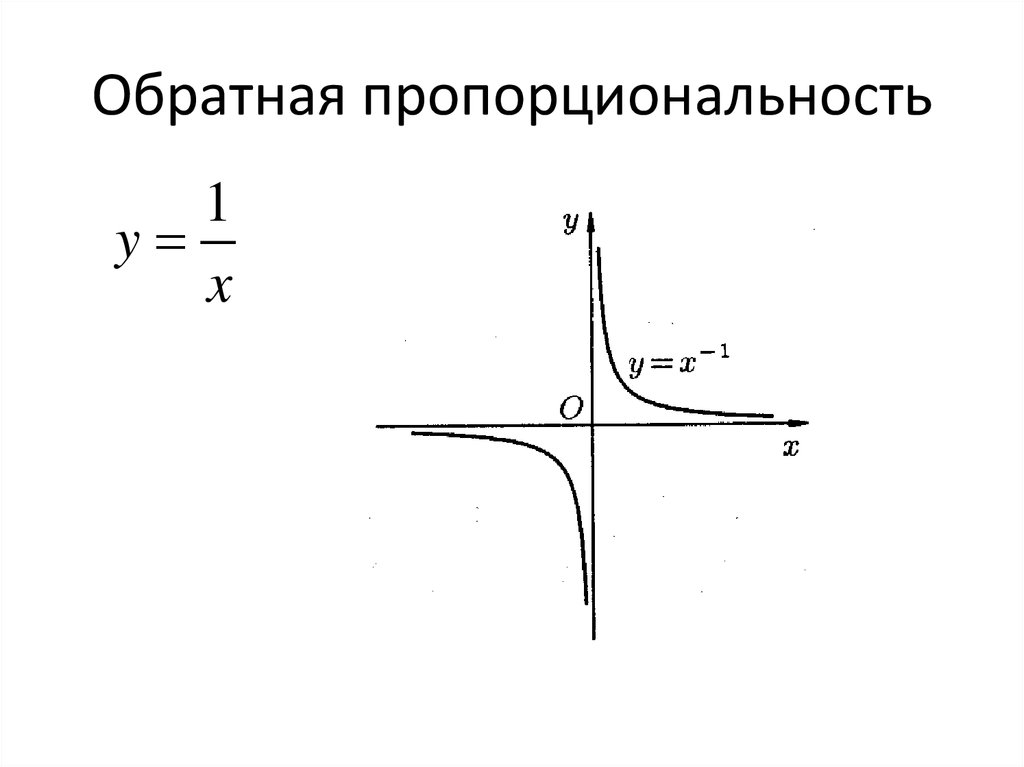
Кубическая парабола при 326. Обратная пропорциональность
1y
x
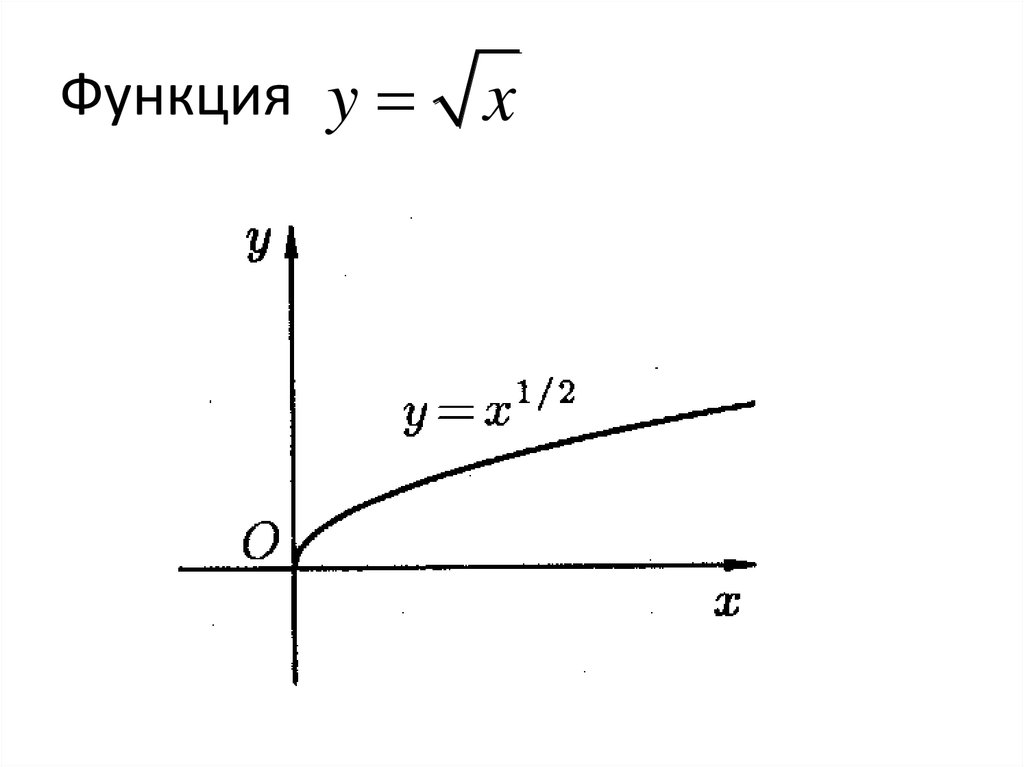
27. Функция
yx
28.
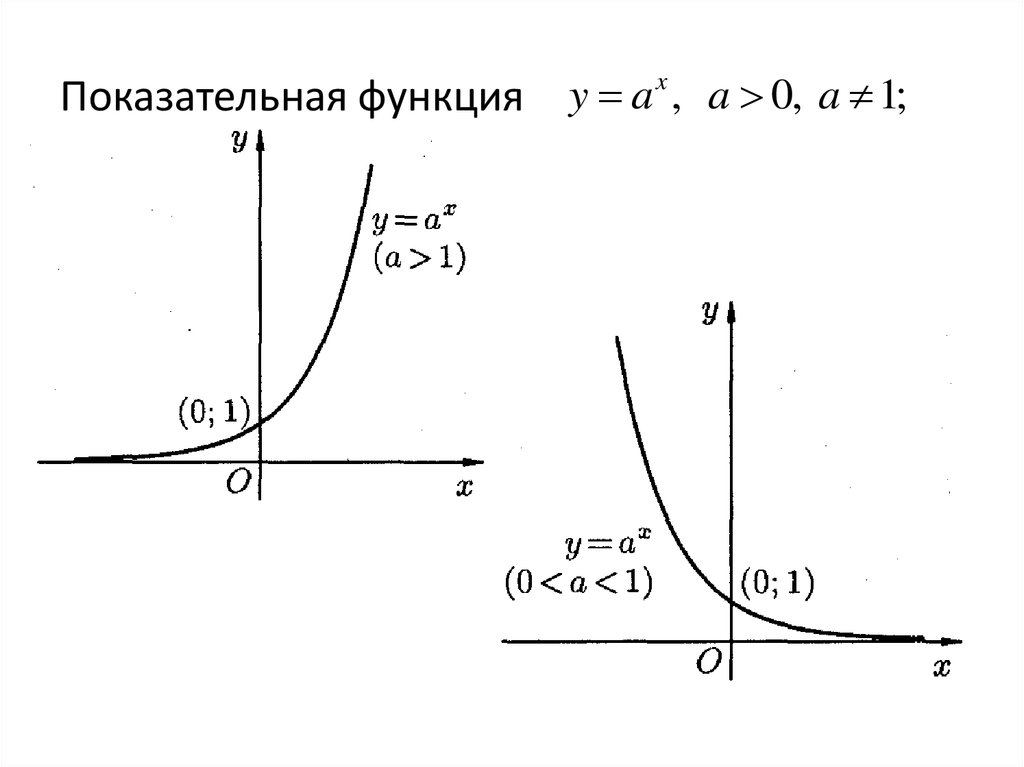
Показательная функция y a , a 0, a 1;x
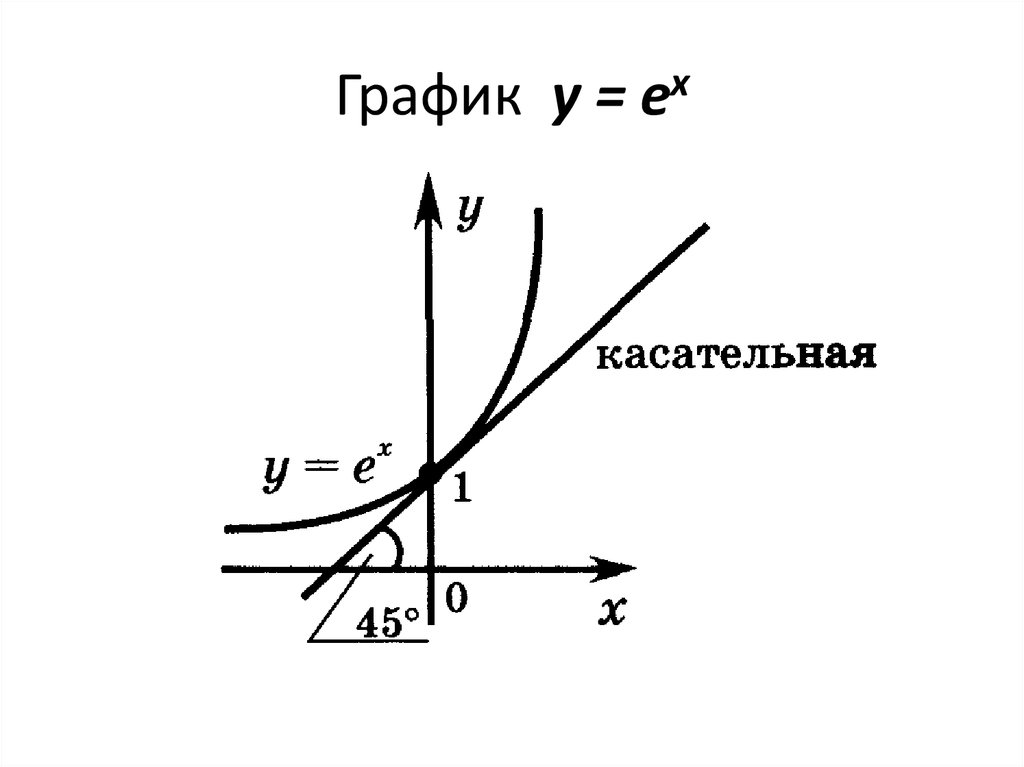
29. Показательная функция у = ех
Показательная функция у = ех,где е = 2,71828 — число е,
называется экспоненциальной, или
экспонентой.
у = ех = ехр(х) —
«экспонента от x».
30. График у = ех
31.
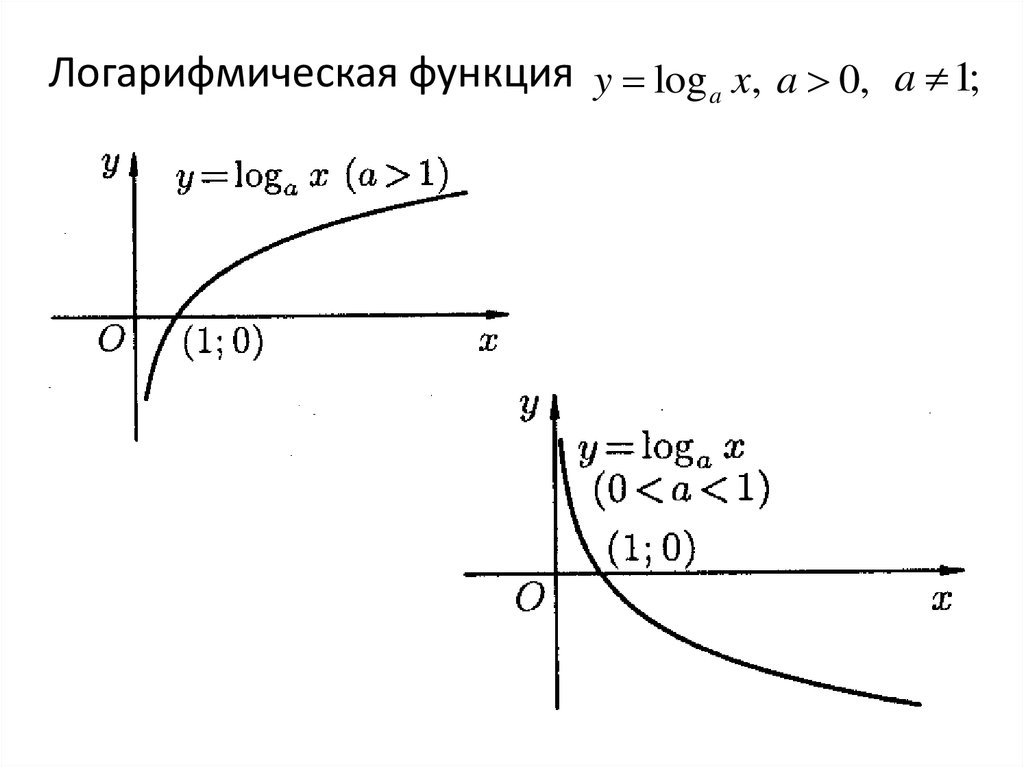
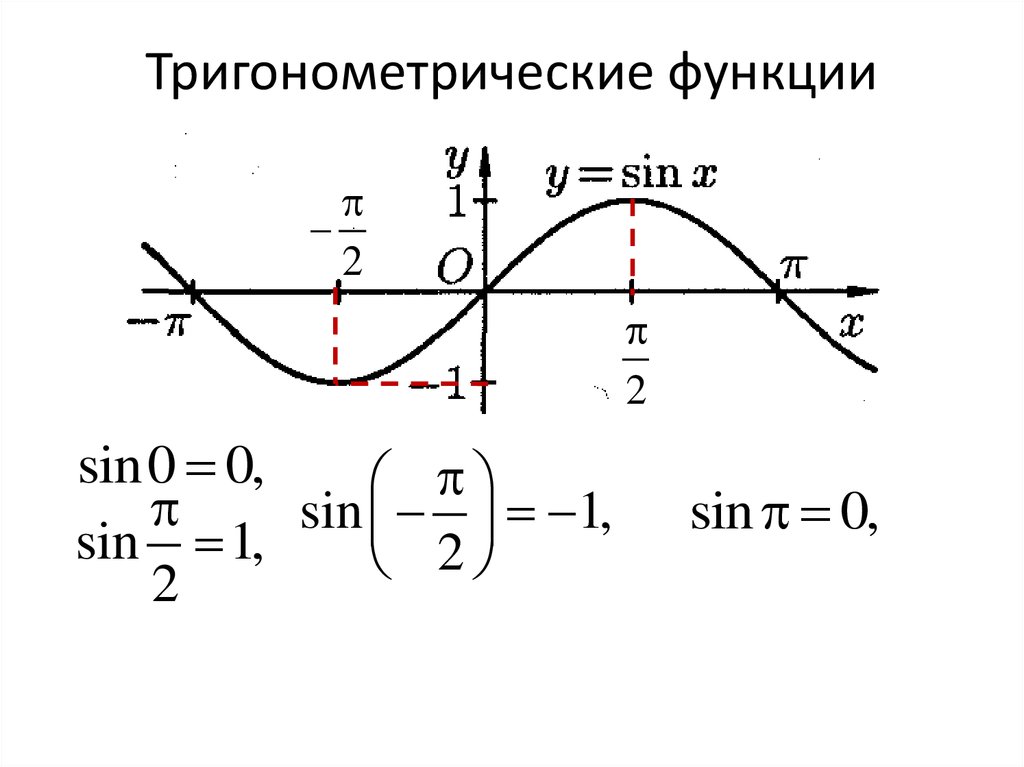
Логарифмическая функция y log a x, a 0, a 1;32. Тригонометрические функции
22
sin0 0,
sin 1,
sin 1,
2
2
sin 0,
33.
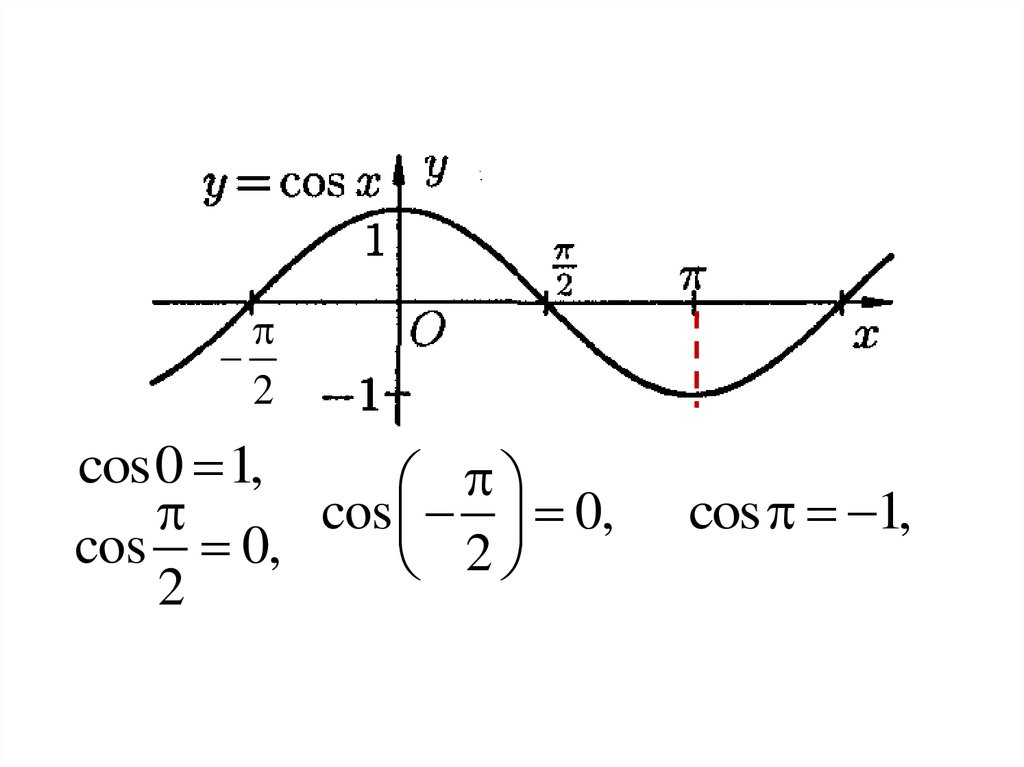
2cos0 1,
cos 0,
cos 0,
2
2
cos 1,
34.
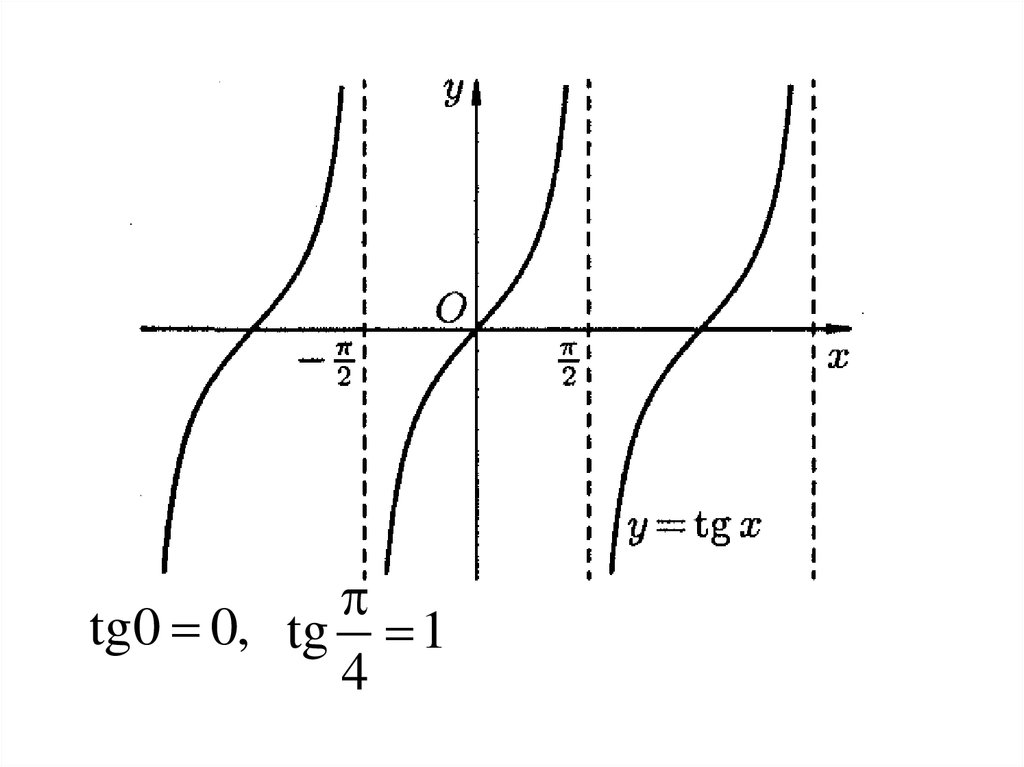
tg0 0, tg 14
35.
2ctg 0, ctg 1
4
2
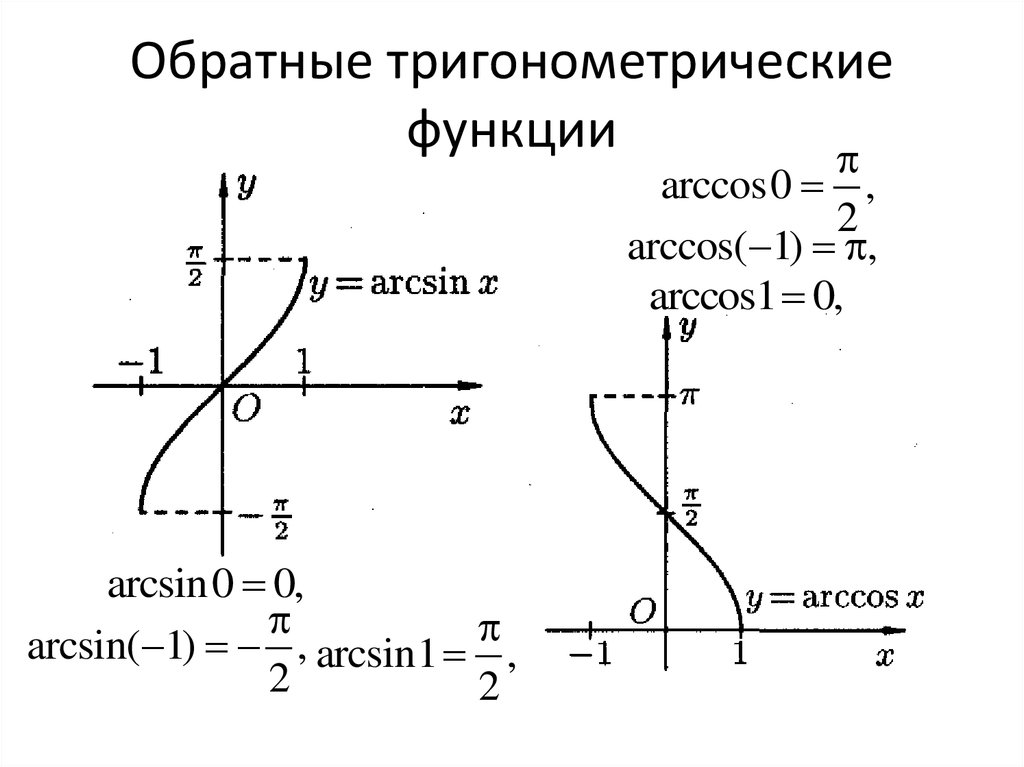
36. Обратные тригонометрические функции
arccos0 ,2
arccos( 1) ,
arccos1 0,
arcsin0 0,
arcsin( 1) , arcsin1 ,
2
2
37.
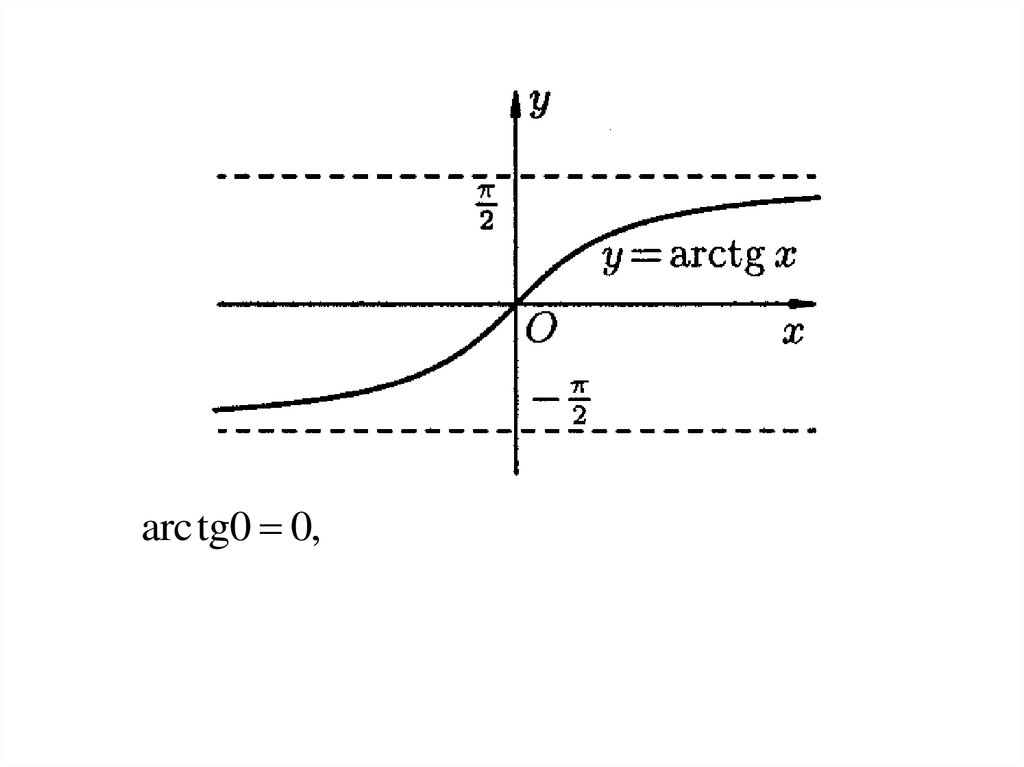
arc tg0 0,38.
arcctg0 ,2
39.
Элементарнымифункциями
называются все функции, которые можно
получить из основных элементарных
функций с помощью конечного числа
арифметических действий с применением
действительных
коэффициентов
и
образования сложной функции.
40.
Некоторые элементарные функции:1) линейная функция y ax b.
2
y
ax
bx c.
2) квадратичная функция
3)
многочлены
с
действительными
коэффициентами (целые рациональные
функции)
Pn ( x ) an x n an 1 x n 1 ... a1 x a0
4)
дробно-рациональные
(рациональные дроби) –
многочленов: R( x ) Pn ( x )
Qm ( x )
функции
отношение
41.
5) иррациональные функции - функции вкоторых используется операция извлечения
корня.
Некоторые неэлементарные функции:
1.
1, x 0,
y sign x 0, x 0,
1, x 0.
2. Дробная часть y {x} x [ x]
42. Квадратичная функция
Квадратичной функцией называется функциявида
Область определения функции, т.е. все
значения, которые может принимать х, – все
действительные числа.
Нули квадратичной функции – все значения х,
при которых у=0, т.е. корни квадратного
уравнения ах2+bх+с=0.
43.
График квадратичной функцииЛюбую квадратичную функцию
y ax bx c
2
можно представить в виде
y ax bx c a( x x0 ) y0
2
b
x0
2a
2
b 4ac
y0
4a
2
44.
График функции y a ( x x0 ) y0 —парабола.
2
Вершина параболы y a ( x x0 ) y0 —
точка O( x0 ; y 0 ) .
Ось симметрии — прямая x x 0
Область значений — интервал [ y 0 ; ) ,
если a 0
или ( ; y 0 ] , если a 0
2
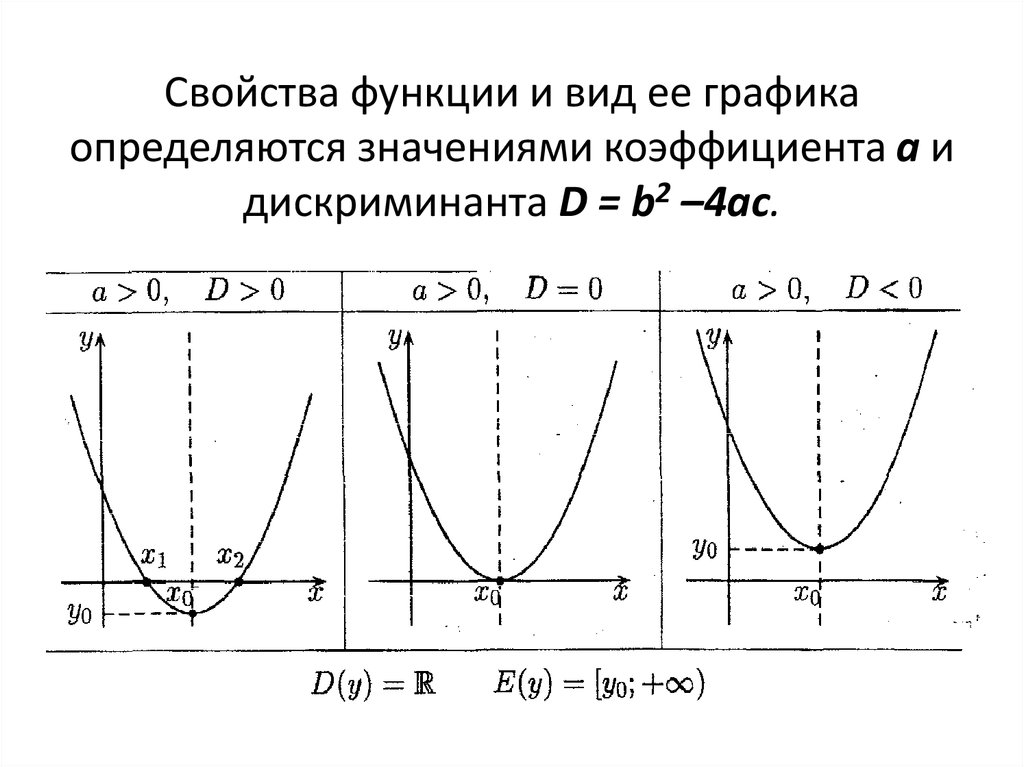
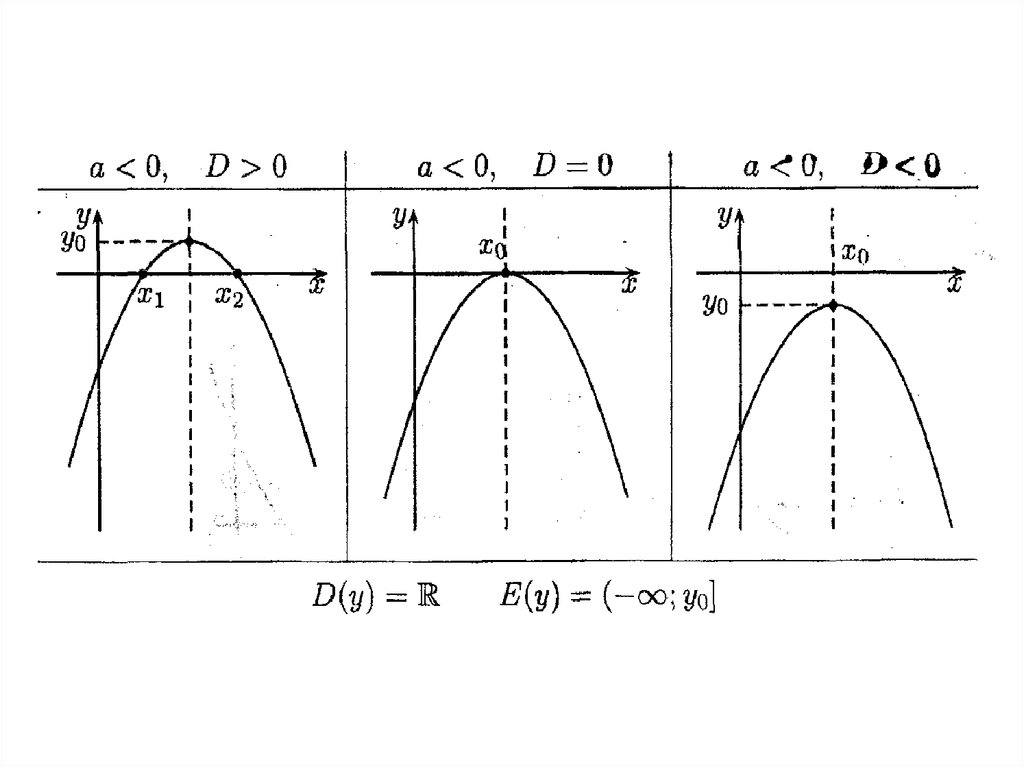
45. Свойства функции и вид ее графика определяются значениями коэффициента а и дискриминанта D = b2 –4ас.
46.
47.
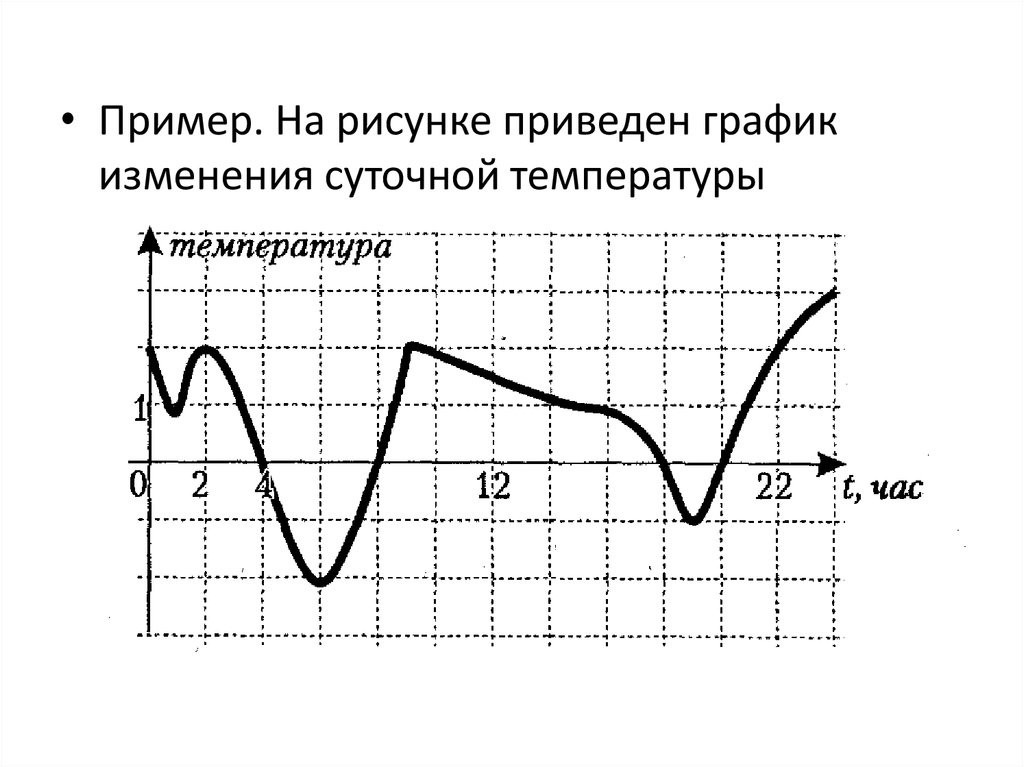
• Пример. На рисунке приведен графикизменения суточной температуры
48.
Определите:a) максимальное и минимальное значение
температуры;
b) в какое время температура была равна нулю;
c)
временные
промежутки,
на
которых
температура была положительная;
d) промежутки, на которых температура была
отрицательная;
e) наибольший промежуток времени, на котором
температура не меняла своего знака;
f) промежутки возрастания температуры;
g) промежутки убывания температуры.




























 mathematics
mathematics








