Reshenie_zadach_na_ploschad_OGE

1. Решение заданий 18. фигуры на квадратно й решетке

Решение заданий
18. фигуры на
квадратной решетке
Готовимся к ОГЭ

2.

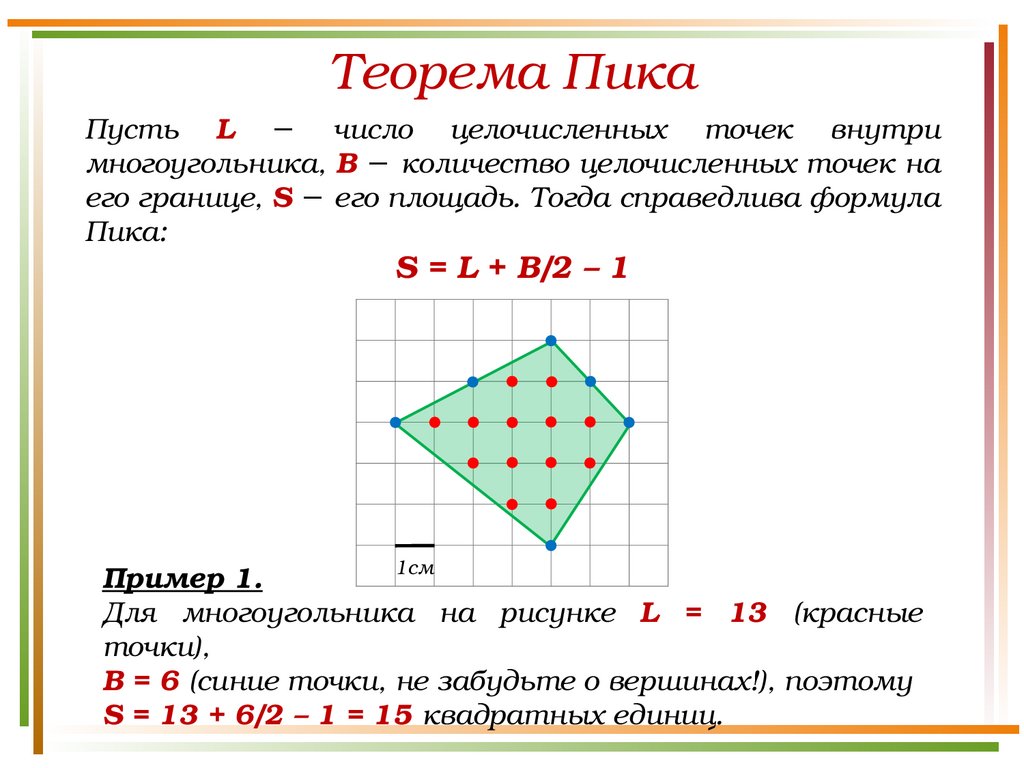
Теорема Пика
Пусть L − число целочисленных точек внутри
многоугольника, B − количество целочисленных точек на
его границе, S − его площадь. Тогда справедлива формула
Пика:
S = L + B/2 – 1
1см
Пример 1.
Для многоугольника на рисунке L = 13 (красные
точки),
B = 6 (синие точки, не забудьте о вершинах!), поэтому
S = 13 + 6/2 – 1 = 15 квадратных единиц.

3.

Теорема Пика
1см
Пример 2.
L = 18 (красные точки),
B = 10 (синие точки), поэтому
S = 18 + 10/2 – 1 = 22
квадратных единиц.

4.

Площадь прямоугольного треугольника
Пусть
а
и
b
−
катеты
прямоугольного
треугольника, c – гипотенуза, h – высота,
проведенная
из
вершины
прямого
угла
на
гипотенузу, S − его площадь.
Тогда справедливы формулы:
S=
1
ab
2
S=
1
ch
2
a
h
b
c

5.

Площадь произвольного треугольника
Пусть а − сторона треугольника, hа – высота,
проведенная к этой стороне, S − его площадь.
Тогда справедлива формула:
1
S = aha
2
ha
a
ha
a

6.

Площадь параллелограмма
Пусть а − сторона параллелограмма, hа –
высота, проведенная к этой стороне, S − его
площадь.
Тогда справедлива формула:
S = aha
ha
a
ha
a

7.

Площадь трапеции
Пусть а и b − основания трапеции, h – высота,
S − площадь трапеции.
Тогда справедлива формула:
a+b
S=
h
2
a
h
a
h
b
b

8.

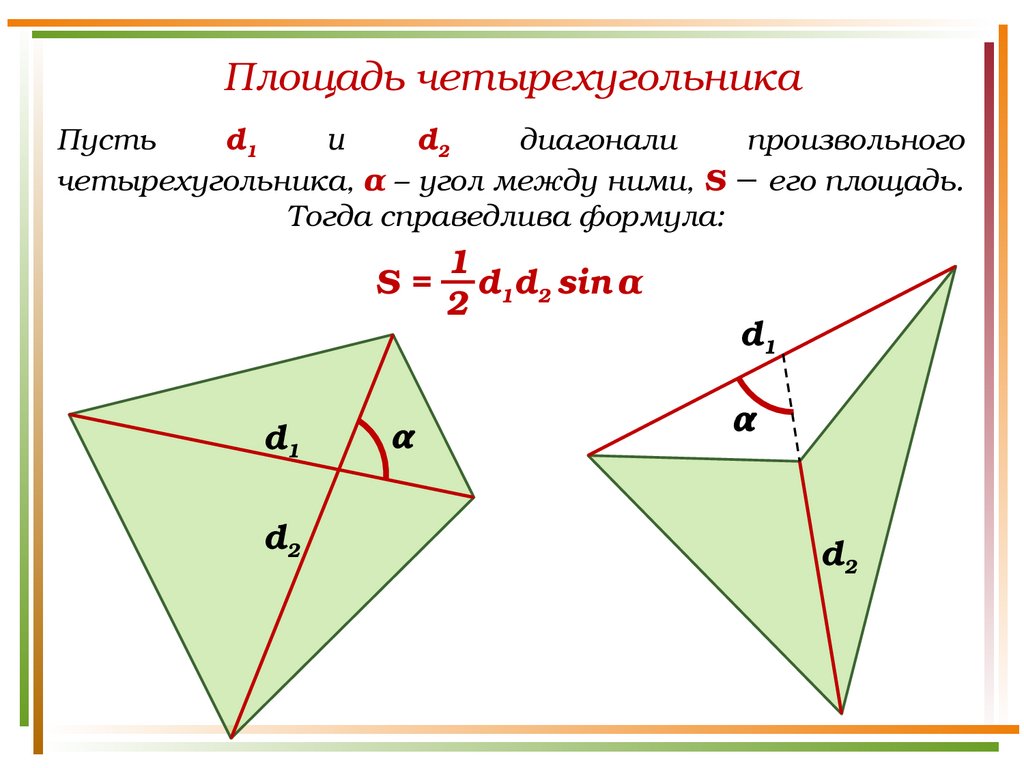
Площадь четырехугольника
Пусть
d1
и
d2
диагонали
произвольного
четырехугольника, α – угол между ними, S − его площадь.
Тогда справедлива формула:
S=
1
d1d2 sin α
2
d1
d1
d2
d2

9.

Площадь круга
Пусть R − радиус круга, d = 2R – диаметр,
С = 2πR – длина окружности, S − его
площадь.
Тогда справедливы2 формулы:
S = πR
S=
1
πd2
4
S=
R
О
d
1
Сd
4

10.

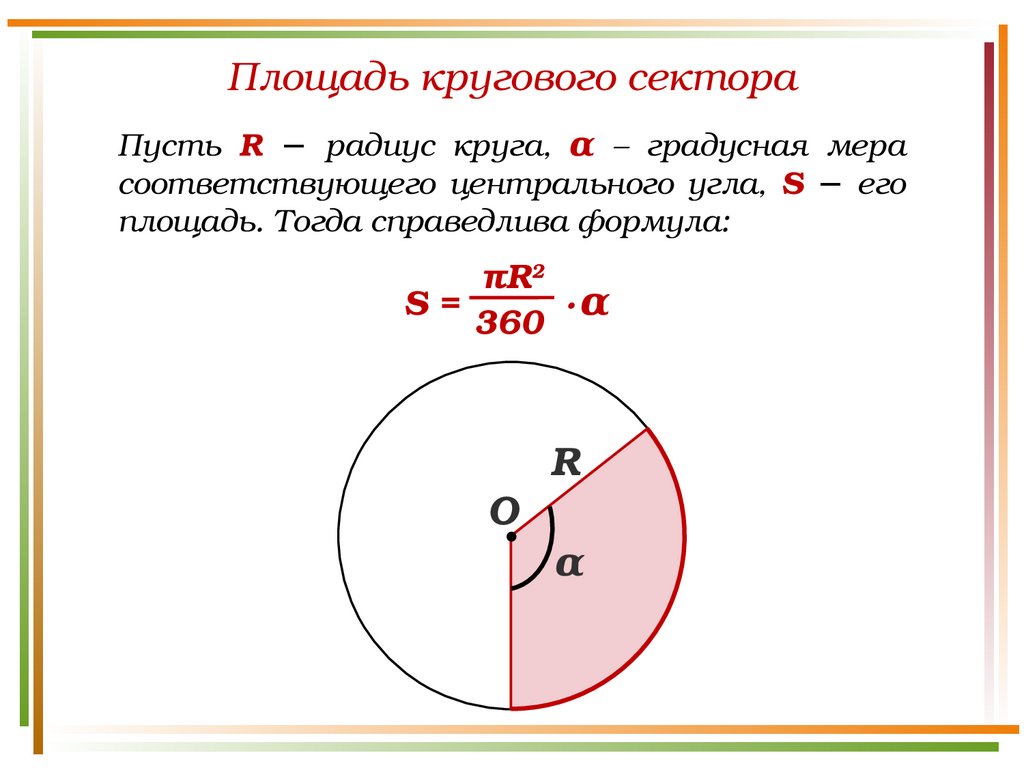
Площадь кругового сектора
Пусть R − радиус круга, α – градусная мера
соответствующего центрального угла, S − его
площадь. Тогда справедлива формула:
πR2
S=
·α
360
О
R
α

11.

Площадь кольца
Пусть R − радиус внешней окружности, r – радиус
внутренней окружности, S − его площадь.
Тогда справедлива формула:
S = π(R2 – r2)
r
О
R

12.

Задания открытого банка задач
1. Найдите площадь треугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
3
Решение:
1
S ab
2
1
S 3 7 10,5.
2
7
1см
Ответ: 10,5.

13.

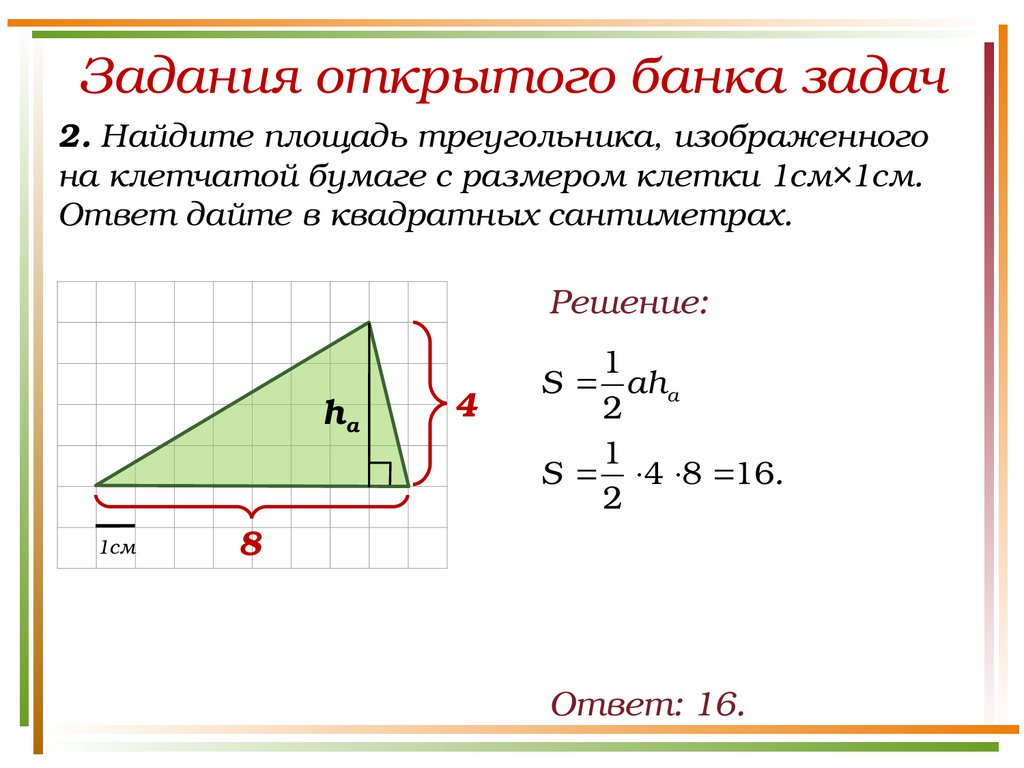
Задания открытого банка задач
2. Найдите площадь треугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
Решение:
ha
1см
4
1
S aha
2
1
S 4 8 16.
2
8
Ответ: 16.

14.

Задания открытого банка задач
3. Найдите площадь треугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
Решение:
ha
3
1см
8
1
S aha
2
1
S 3 8 12.
2
Ответ: 12.

15.

Задания открытого банка задач
4. Найдите площадь треугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
Решение:
1см
4
ha
1
S aha
2
1
S 4 6 12.
2
6
Ответ: 12.

16.

Задания открытого банка задач
5. Найдите площадь треугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
Решение:
1см
3
ha
1
S aha
2
1
S 3 8 12.
2
8
Ответ: 12.

17.

Задания открытого банка задач
6. Найдите площадь треугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
8
1
Решение:
S Δ Sп/у S Δ1 S Δ2 S Δ3
1
8 1
2
1
1
8 2
9 6
2
2
S Δ 8 9
9
8
2
6
1см
8
72 4 27 8 33.
Ответ: 33.

18.

Задания открытого банка задач
7. Найдите площадь треугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
1
7
Решение:
S Δ Sп/у S Δ1 S Δ2 S Δ3 Sп / у1
4
9
5
1
S Δ 8 9 8 9
2
1
1
7 4
5 1 4 1
2
2
72 36 14 2,5 4 15,5.
1см
8
Ответ: 15,5.

19.

Задания открытого банка задач
8. Найдите площадь квадрата, изображенного на
клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
7
1
Решение:
S a 2
по теореме Пифагора:
а
а 2 72 12 49 1 50
S 50
а
1см
Ответ: 50.

20.

Задания открытого банка задач
9. Найдите площадь прямоугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
Решение:
6
b
а
1см
1
2
S ab
по теореме Пифагора:
3
а 40
а 2 62 22 36 4 40
b 2 32 12 9 1 10
b 10
S 40 10 400 20
Ответ: 20.

21.

Задания открытого банка задач
10. Найдите площадь ромба, изображенного на
клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
Решение:
4
1см
1
S d1 d2
2
1
S 8 4 16
2
8
Ответ: 16.

22.

Задания открытого банка задач
11. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
Решение:
S S Δ1 S Δ2
4
3
1см
5
1
1
S ah1 ah 2
2
2
1
S a h1 h 2
2
1
35
S 5 4 3
17,5
2
2
Ответ: 17,5.

23.

Задания открытого банка задач
12. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
8
Решение:
S S Δ1 S Δ2
4
6
1см
1
1
S ah1 ah 2
2
2
1
S a h1 h 2
2
1
S 8 6 4 8
2
Ответ: 8.

24.

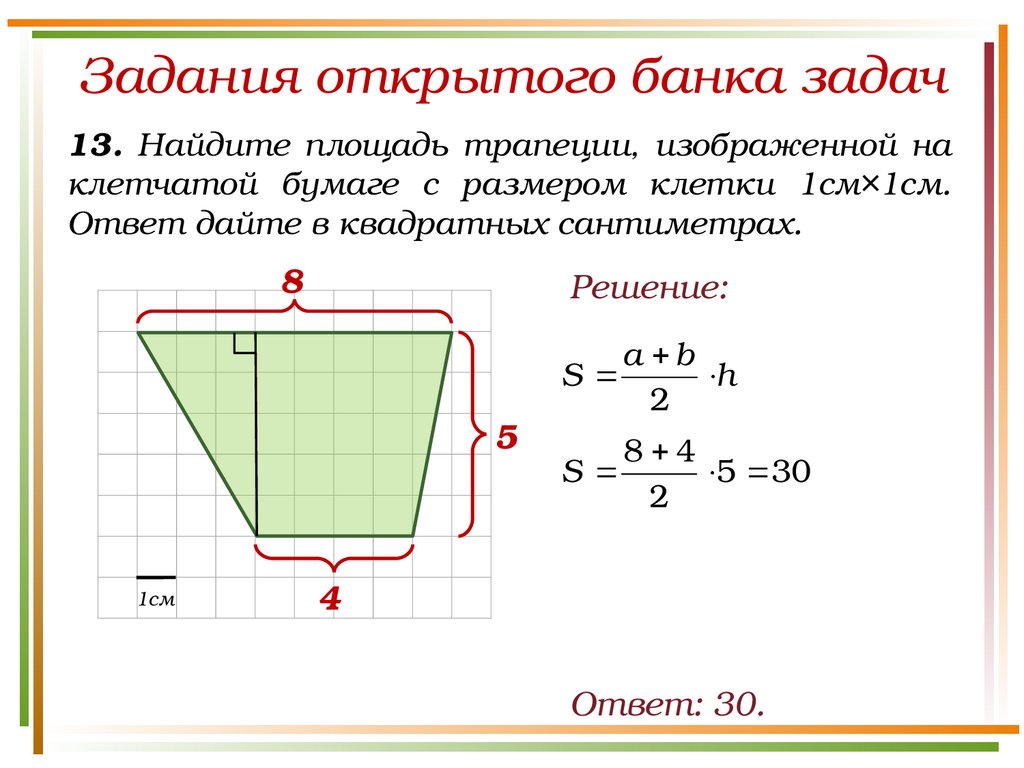
Задания открытого банка задач
13. Найдите площадь трапеции, изображенной на
клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
8
Решение:
5
1см
S
a b
h
2
S
8 4
5 30
2
4
Ответ: 30.

25.

Задания открытого банка задач
14. Найдите площадь трапеции, изображенной на
клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
8
Решение:
a b
S
h
2
2
7
7 2
S
8 36
2
1см
Ответ: 36.

26.

Задания открытого банка задач
15.
Найдите
изображенного на
клетки 1см×1см.
сантиметрах.
площадь
параллелограмма,
клетчатой бумаге с размером
Ответ дайте в квадратных
Решение:
S aha
7
S 4 7 28
1см
4
Ответ: 28.

27.

Задания открытого банка задач
17. Найдите площадь треугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
3
5
2
9
7
Решение:
S Δ Sп/у S Δ1 S Δ2 S Δ3
1
S Δ 8 9 3 9
2
1
1
7 8
5 2
2
2
72 13,5 28 5 25,5.
1см
8
Ответ: 25,5.

28.

Задания открытого банка задач
18. Найдите площадь трапеции, изображенной на
клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
Решение: (1 способ)
7
S S Δ1 S Δ2
3
1см
2
1
1
S ah1 ah 2
2
2
1
S a h1 h 2
2
1
27
S 3 7 2
13,5
2
2
Ответ: 13,5.

29.

Задания открытого банка задач
18. Найдите площадь трапеции, изображенной на
клетчатой бумаге с размером клетки 1см×1см.
Ответ дайте в квадратных сантиметрах.
Решение: (2 способ)
9
a b
Sтрапеции
h
2
9 2
S1
7 38,5
S2
4
2
9 2
7
S2
4 22
2
S3 2
1
S 3 2 2 2
2
1
1
1см
S4 S 4 2 2 1 1
2
S S1 S 2 S 3 S 4 38,5 22 2 1 13,5
Ответ: 13,5.

30.

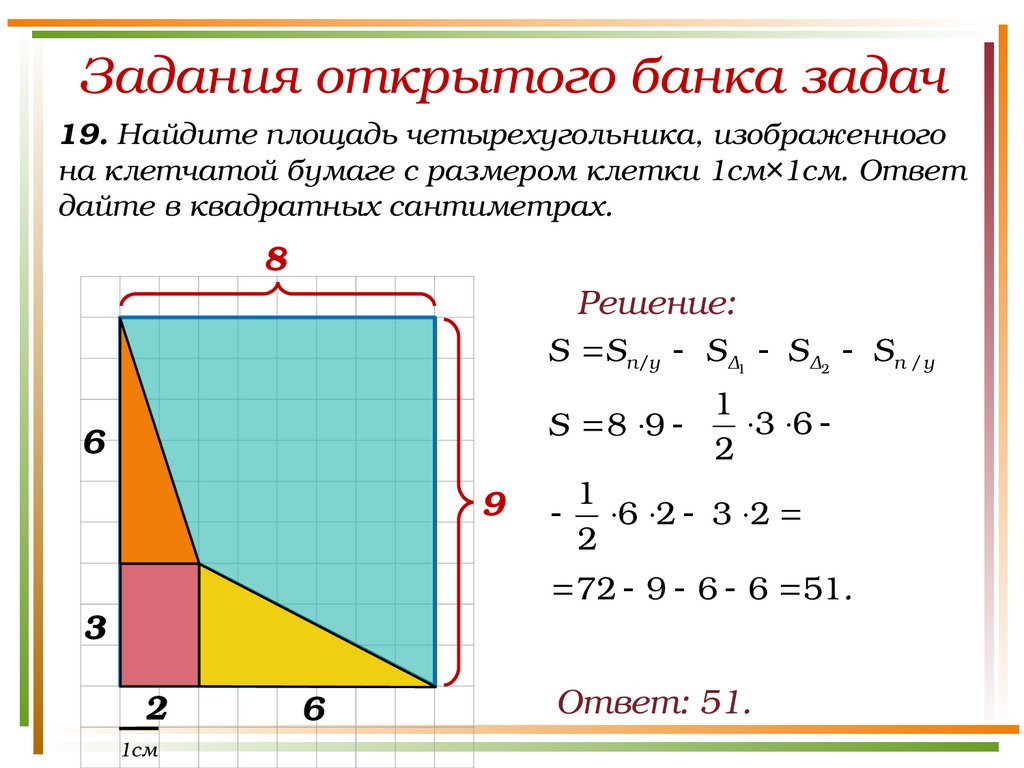
Задания открытого банка задач
19. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
8
Решение:
S Sп/у S Δ1 S Δ2 Sп / у
6
9
1
3 6
S 8 9
2
1
6 2 3 2
2
72 9 6 6 51.
3
2
1см
6
Ответ: 51.

31.

Задания открытого банка задач
20. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
2
Решение:
S Sп/у S Δ1 S Δ2
5
9
1
1
5 2
8 9
S 8 9
2
2
72 36 5 31.
1см
8
Ответ: 31.

32.

Задания открытого банка задач
21. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
Решение:
8
2
7
5
S Sп/у S Δ1 S Δ2 S Δ3
1
5 3
S 8 7
2
1
1
8 2 7 2
2
2
56 7,5 8 7 33,5.
2
1см
3
Ответ: 33,5.

33.

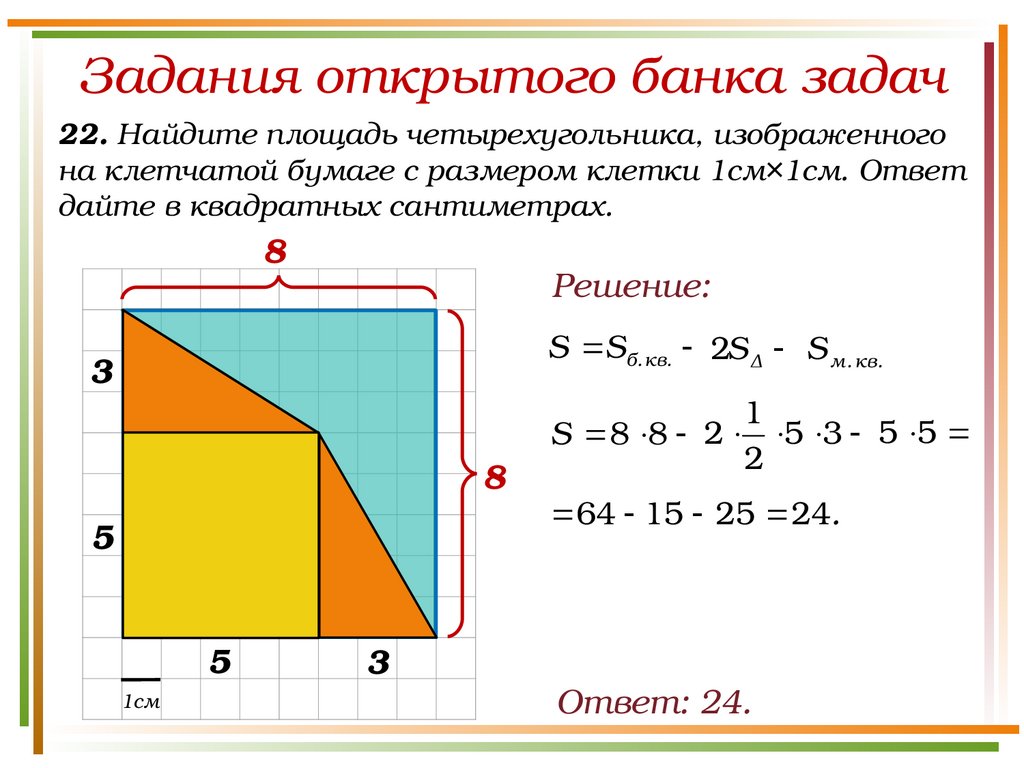
Задания открытого банка задач
22. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
8
Решение:
S Sб. кв. 2S Δ S м . кв .
3
8
5
5
1см
3
1
S 8 8 2 5 3 5 5
2
64 15 25 24.
Ответ: 24.

34.

Задания открытого банка задач
23. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
8
Решение:
4
7
3
3
1см
5
S Sп/у S Δ1 S Δ2 Sп / у
1
7 3
S 8 7
2
1
8 4 5 3
2
56 10,5 16 15 14,5.
Ответ: 14,5.

35.

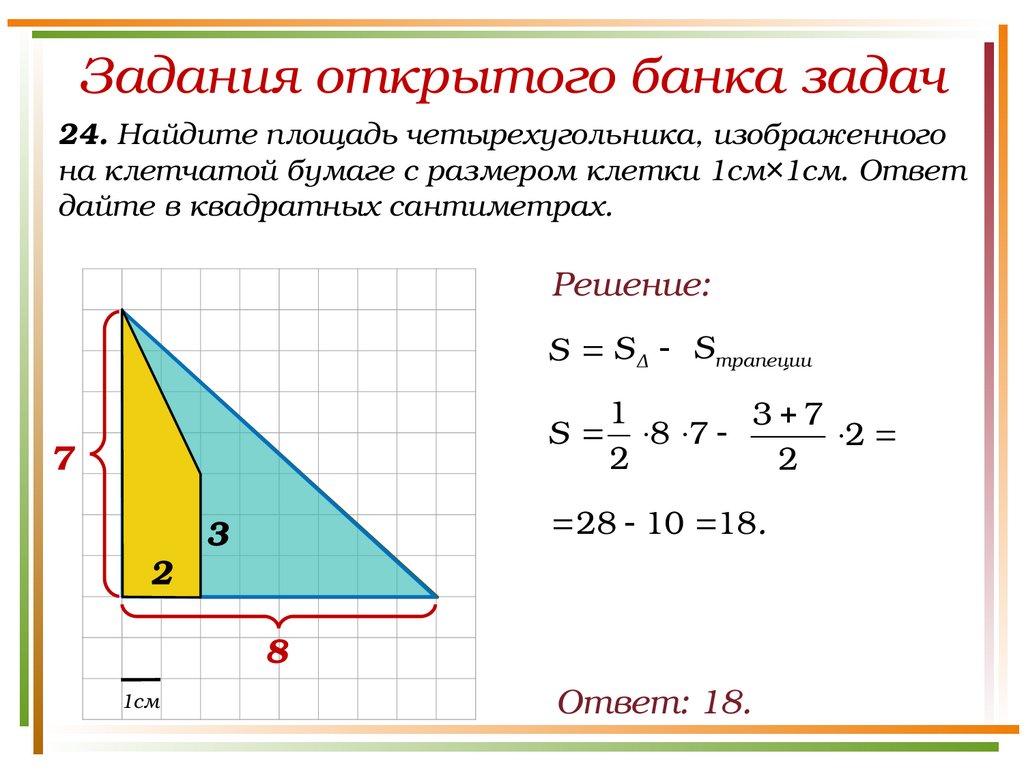
Задания открытого банка задач
24. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
Решение:
S S Δ Sтрапеции
1
3 7
S 8 7
2
2
2
7
2
28 10 18.
3
8
1см
Ответ: 18.

36.

Задания открытого банка задач
25. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
Решение: (1 способ)
4
4
4√
2
4√
2
1см
4
4
Площадь четырехугольника
(в том числе невыпуклого)
равна половине произведения
диагоналей на синус угла
между ними.
Диагонали данного
четырехугольника являются
взаимно перпендикулярными
диагоналями квадратов со
стороной 4. Поэтому длины
диагоналей равны 4√2, а синус
угла между ними равен 1.
Тем самым, площадь данного
четырехугольника равна 16.
Ответ: 16.

37.

Задания открытого банка задач
26. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
Решение: (2 способ)
L = 15 (красные точки),
B = 4 (синие точки),
тогда по теореме Пика
S = L + B/2 – 1
S = 15 + 4/2 – 1 = 16
1см
Ответ: 16.

38.

Задания открытого банка задач
27. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
6
Решение: (1 способ)
3
4
5
Sтрап.
1
1
5 6
9 4
9
2
2
3 5
1
4
5 5
2
2
S 9 9
5
5
4
S Sкв. S Δ1 S Δ2 S Δ3
81 15 18 12,5 16 19,5.
1см
9
Ответ: 19,5.

39.

Задания открытого банка задач
28. Найдите площадь четырехугольника, изображенного
на клетчатой бумаге с размером клетки 1см×1см. Ответ
дайте в квадратных сантиметрах.
Решение: (2 способ)
L = 16 (красные точки),
B = 9 (синие точки),
тогда по теореме Пика
S = L + B/2 – 1
S = 16 + 9/2 – 1 = 19,5
1см
Ответ: 19,5.

40.

Задания открытого банка задач
29. Найдите площадь S фигуры, изображенной на
клетчатой бумаге с размером клетки 1см×1см.
В ответе запишите S/π.
Решение:
R
3
3
5
5
Sсектора Sкруга πR 2
8
8
по теореме Пифагора:
R 2 32 32 18
Sсектора
π
5
18π 11,25.
8π
1см
Ответ: 11,25.

41.

Задания открытого банка задач
30. Найдите площадь S круга, считая стороны
квадратных клеток равными 1. В ответе
укажите S/π.
Решение:
Sкруга πR 2
R
О 1
2
по теореме Пифагора:
R 2 22 12 5
Sкруга
π
5π
5.
π
1см
Ответ: 5.

42.

Задания открытого банка задач
31.
Найдите
(в
см2)
площадь
S
фигуры,
изображенной на клетчатой бумаге с размером
клетки 1см×1см.
В ответе запишите S/π.
Решение:
S Sб . круга S м . круга
R
1
1см
2
r
3
3
S πR 2 πr 2 π R 2 r 2
по теореме Пифагора:
R 2 32 32 18
r 2 22 12 5
S π 18 5
13.
π
π
Ответ: 13.

43.

Задания открытого банка задач
32. На клетчатой бумаге нарисованы два круга.
Площадь внутреннего круга равна 12. Найдите
площадь заштрихованной фигуры.
Решение:
Sб . круга πR 2 R 2
2 2
S м . круга πr
r
R
R2
4
16
2
r
r
r
R
Sб . круга
16
S м . круга
Sб . круга 16 S м . круга 16 12 192
Sкольца Sб . круга S м . круга
Sкольца 192 12 180
Ответ: 180.

44.

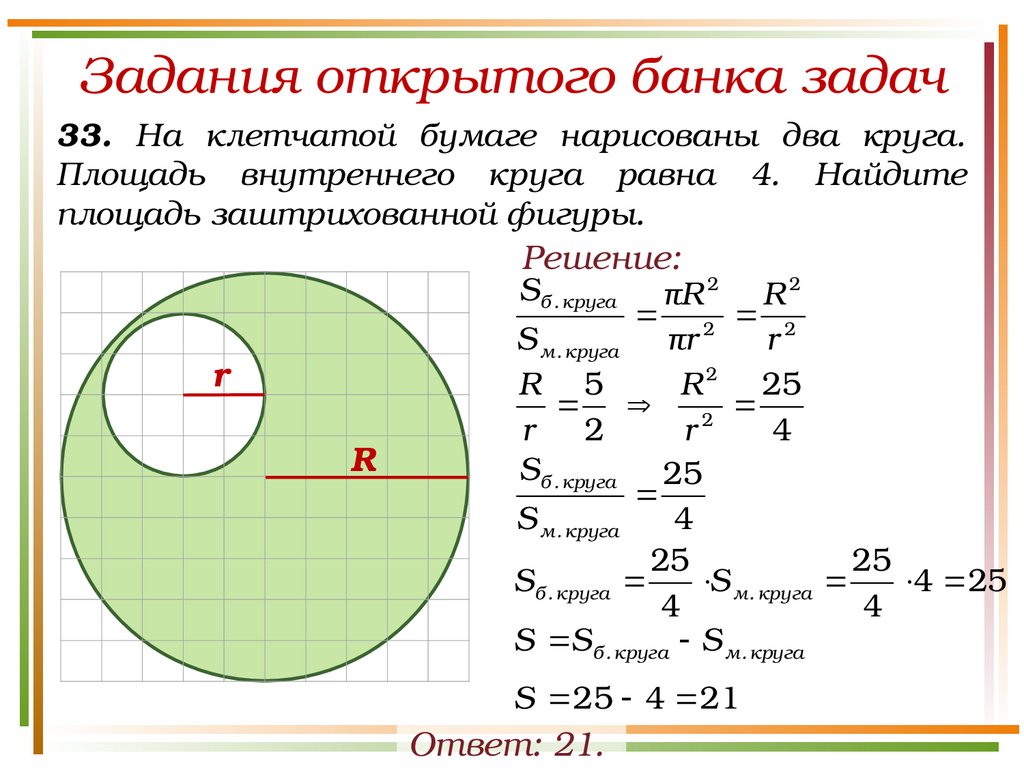
Задания открытого банка задач
33. На клетчатой бумаге нарисованы два круга.
Площадь внутреннего круга равна 4. Найдите
площадь заштрихованной фигуры.
Решение:
Sб . круга πR 2 R 2
2 2
S м . круга πr
r
r
R 5
R 2 25
2
r
2
r
4
R
Sб . круга 25
S м . круга
4
25
25
Sб . круга
S м . круга
4 25
4
4
S Sб . круга S м . круга
S 25 4 21
Ответ: 21.

45.

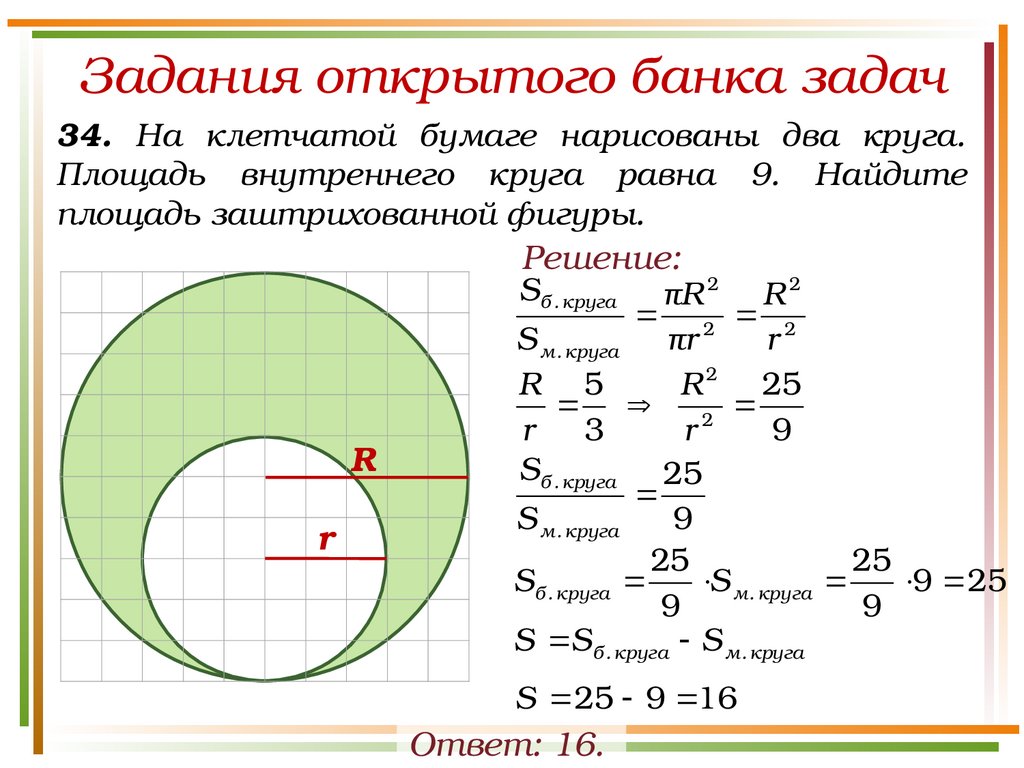
Задания открытого банка задач
34. На клетчатой бумаге нарисованы два круга.
Площадь внутреннего круга равна 9. Найдите
площадь заштрихованной фигуры.
Решение:
Sб . круга πR 2 R 2
2 2
S м . круга πr
r
R 5
R 2 25
2
r
3
r
9
R
Sб . круга 25
S м . круга
9
r
25
25
Sб . круга
S м . круга
9 25
9
9
S Sб . круга S м . круга
S 25 9 16
Ответ: 16.

46.

Задания открытого банка задач
35. На клетчатой бумаге нарисован круг
площадью 93. Найдите площадь заштрихованного
сектора.
Решение:
М
α
С
R
О
R
Найдем величину смежного
с центральным угла α:
СО
2 1
cos α
α 60
ОМ 4 2
Значит, круговой сектор
имеет величину:
180º − 60º = 120º, что
составляет 1/3 часть круга
1
1
Sсектора Sкруга 93 31
3
3
Ответ: 31.

47.

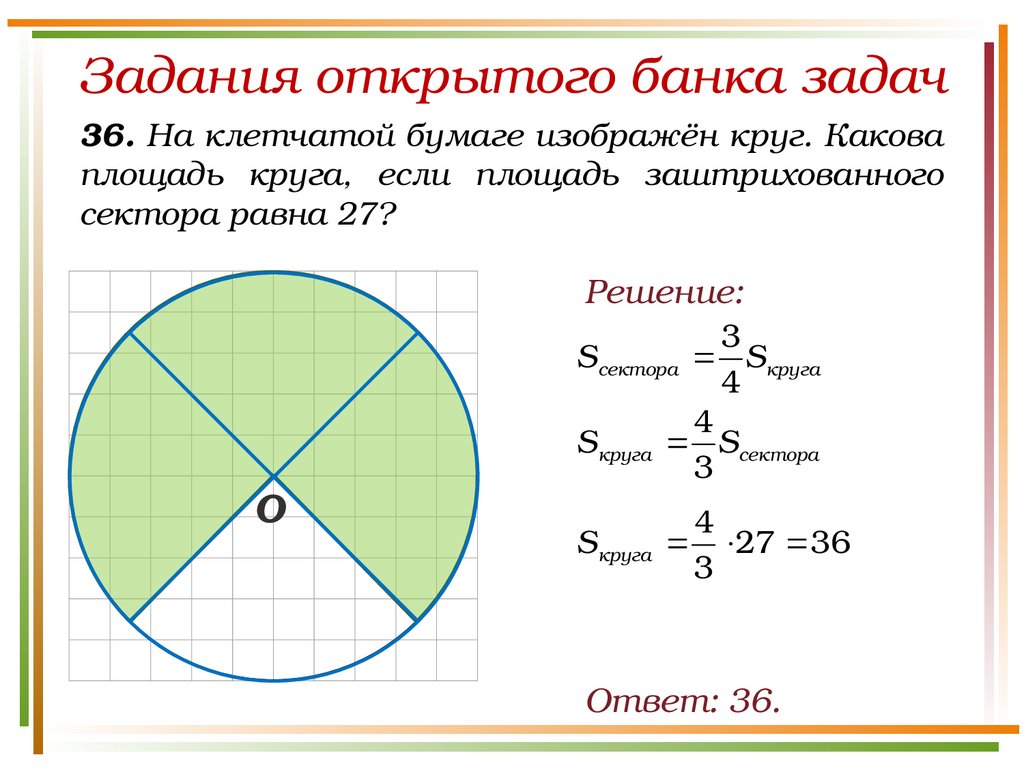
Задания открытого банка задач
36. На клетчатой бумаге изображён круг. Какова
площадь круга, если площадь заштрихованного
сектора равна 27?
Решение:
О
3
Sсектора Sкруга
4
4
Sкруга Sсектора
3
4
Sкруга 27 36
3
Ответ: 36.