Similar presentations:
Введение на основе теорем динамики для точки
1.
ЛЕКЦИИ ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ.ДИНАМИКА
ЛЕКЦИЯ 5
2.
Ознакомиться с общими теоремами динамикиматериальной точки и примерами их практического
применения.
План лекции
Введение
• Теорема об изменении импульса точки
• Теорема об изменении момента импульса точки
• Движение в центральном поле
• Теорема об изменении кинетической энергии точки
• Работа силы. Потенциальные силы
Заключение
2
Цель лекции
3.
теоремы об изменении …импульса
момента импульса
кинетической энергии
Зачем нам нужны теоремы для точки?
оптимальная
методика решения
задач
3
Введение
на основе теорем
динамики для точки
мы построим теоремы
для механической
системы
4.
Импульс (количество движения) точки - вектор,равный произведению массы точки на вектор
ее скорости
P mv
4
Теорема об изменении импульса
v P
5.
Элементарным импульсомсилы называется вектор,
равный произведению силы
на элементарный промежуток
времени
Импульсом силы за
конечный промежуток
времени называется
вектор
5
Теорема об изменении импульса
dS Fdt
t
S Fdt
0
6.
Производная по времени от импульсаматериальной точки равна равнодействующей
приложенных к точке сил
Изменение импульса материальной точки за
некоторый временной интервал равно
импульсу равнодействующей приложенных к
точке сил на этом интервале
6
Теорема об изменении импульса
7.
• Запишем дифф. уравнение движения точки• Учитывая постоянство массы точки и
определение ее ускорения
N
d
получим
(mv ) Fi R ,
dt
i 1
dv
a
,
dt
или
dP
R
dt
• Умножив обе части уравнения на элементарный промежуток
времени и проинтегрировав, получим
tк
dP Rdt
tк
tн
tн
7
Теорема об изменении импульса
или
tк
Pк Pн Rdt
tн
Теорема доказана
8.
Fi 0.N
• Пусть
i 1
• В этом случае
dP
0 , P const
dt
Если равнодействующая приложенных к материальной
точке сил равна нулю, то импульс точки сохраняется во
все время движения
Если проекция на какую-нибудь ось равнодействующей
приложенных к точке сил равна нулю, то проекция
импульса точки на эту ось сохраняется
8
Теорема об изменении импульса
9.
nОпределить время
движения точки до
остановки
v0
N
?
tк
Pк Pн Fi dt
m
i
mg
tн
tк
Pк Pн N mg dt
tк
tн
Pн mg sin dt
tн
9
Теорема об изменении импульса
mv0 mg sin tк
tк v0 / g sin
10.
Момент импульса(момент количества движения) точки вектор, определяемый
KO r mv
равенством
r - радиус-вектор точки, проведенный из
центра O
MO ( F ) r F
10
Теорема об изменении
момента импульса
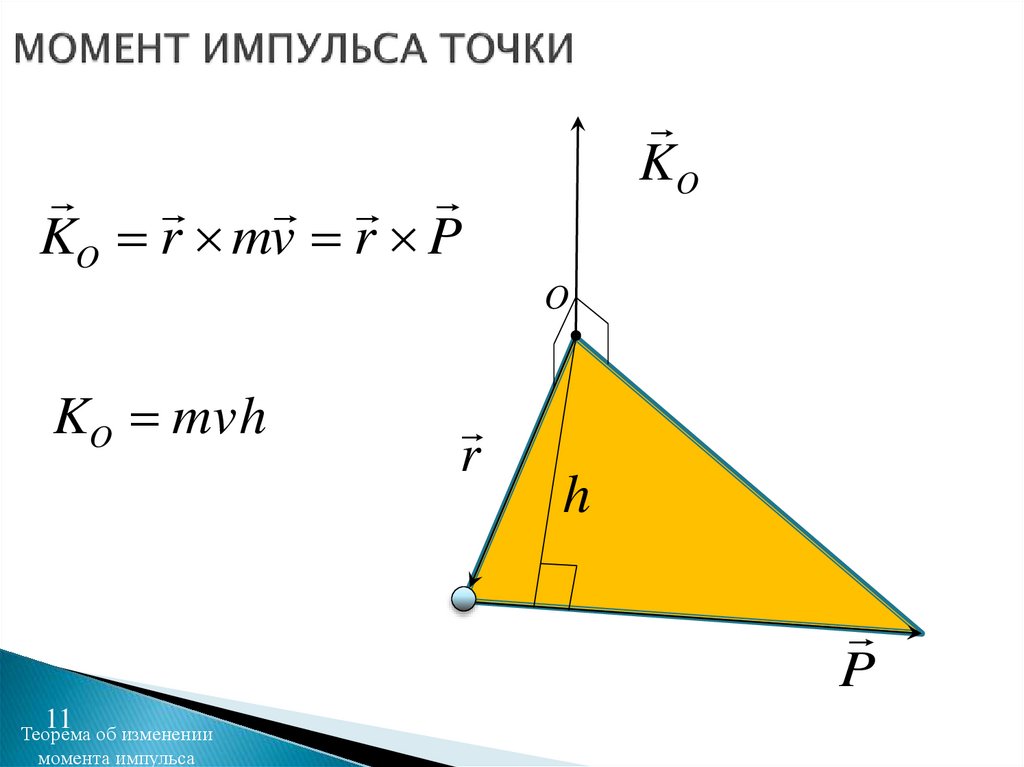
11.
KOKO r mv r P
O
KO mvh
r
h
P
11
Теорема об изменении
момента импульса
12.
Производная по времени от моментаимпульса материальной точки
относительно некоторого неподвижного
центра равна моменту равнодействующей
приложенных к точке сил относительно
этого же центра
12
Теорема об изменении
момента импульса
13.
• Запишем теорему об измененииимпульса точки
d
( mv ) R ,
dt
• Умножим обе части уравнения векторно на радиус-вектор точки
d
r ( mv ) r R M O (R)
dt
d
• Рассмотрим выражение
( r mv )
dt
d
dr
r ( mv )
mv
dt
dt
dK
• Таким образом,
13
Теорема об изменении
момента импульса
O
M O (R )
dt
• Теорема доказана
14.
K x m( yv z zv y )K y m( zv x xv z )
K z m ( xv y yv x )
dK x
M x (R )
dt
14
Теорема об изменении
момента импульса
dK y
dt
dKO
M O (R )
dt
M y (R)
dK z
M z (R )
dt
15.
• Пусть M O ( Fi ) 0.N
i 1
• В этом случае
dKO
0 , KO const
dt
Если момент равнодействующей приложенных к
материальной точке сил относительно какого-либо центра
равен нулю, то момент импульса точки сохраняется
M x ( Fi ) 0
N
i 1
15
Теорема об изменении
момента импульса
dK x
0 , K x const
dt
16.
FДействующую на материальную точку точку
силу называют центральной, если она
всегда направлена к некоторому
неподвижному центру.
Пример
16
Теорема об изменении
момента импульса
?
17.
FКак изменяется модуль скорости планеты при
движении по эллиптической траектории
17
Теорема об изменении
момента импульса
?
18.
Определимзакон изменения
площади сектора d .
dKO
M O ( F ) 0.
dt
F
ds
KO const
модуль
18
Теорема об изменении
момента импульса
O
направление
?
19.
FKO const
O
h
mvh const
ds
m h const
dt
19
Теорема об изменении
момента импульса
ds
d
const
dt
v
20.
dconst
dt
Каждая планета движется в плоскости,
проходящей через центр Солнца, причём за
равные промежутки времени радиус-вектор,
соединяющий Солнце и планету, описывает
равные площади
20
Теорема об изменении
момента импульса
21.
dconst
dt
Иоганн Кеплер (1571 - 1630)
21
Теорема об изменении
момента импульса
22.
скалярная величина, равная половинепроизведения массы точки на квадрат ее
скорости
T mv / 2
2
22
Теорема об изменении энергии
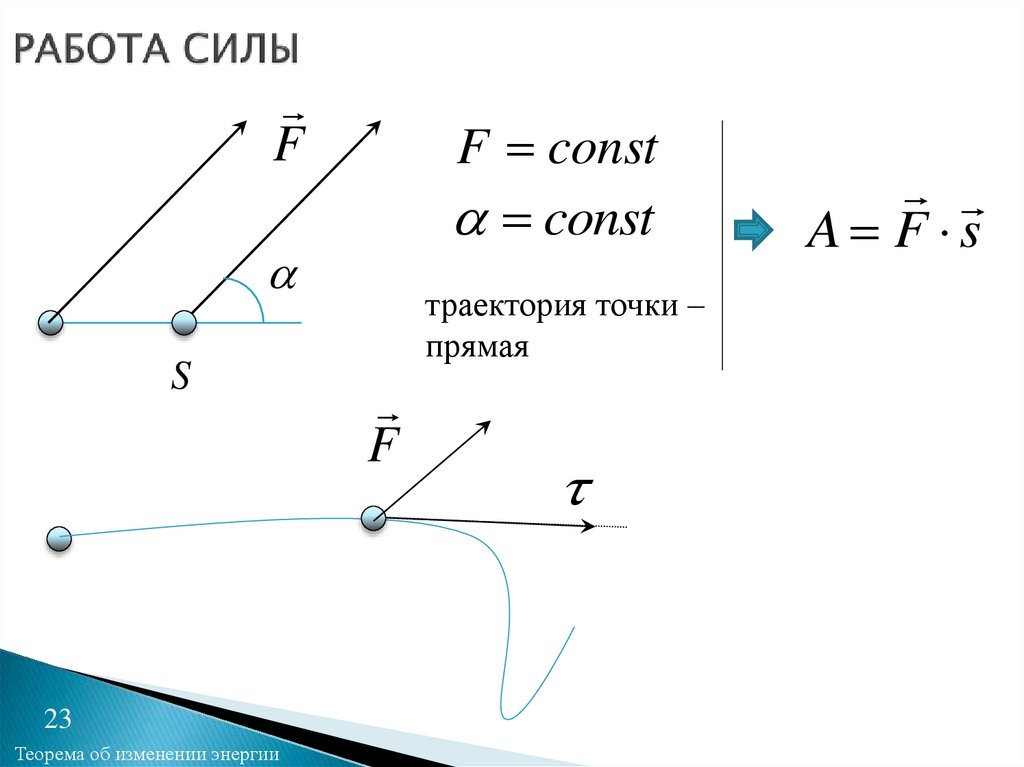
23.
FF const
const
S
23
Теорема об изменении энергии
траектория точки –
прямая
F
A F s
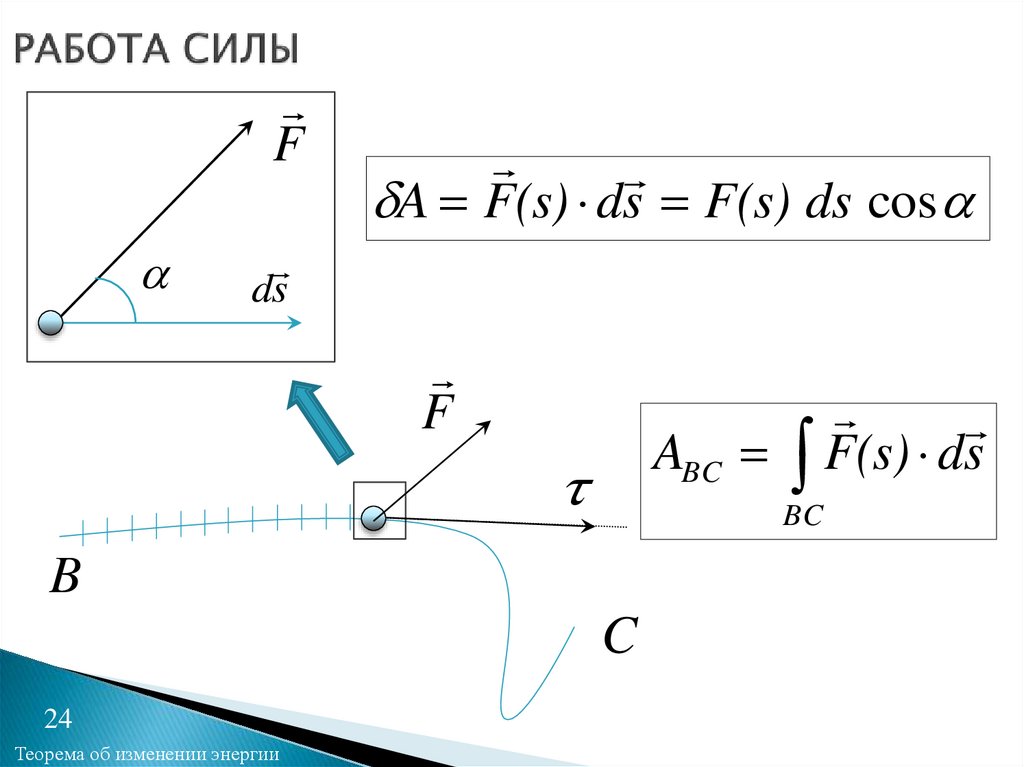
24.
FA F(s) ds F(s) ds cos
ds
F
ABC F(s) ds
BC
B
C
24
Теорема об изменении энергии
25.
Элементарная работа силы –величина, равная скалярному произведению
вектора силы на вектор элементарного
перемещения
A F(s) ds
Работа силы на конечном перемещении –
интеграл от элементарной работы, взятый
вдоль этого перемещения A F(s) ds
BC
BC
25
Теорема об изменении энергии
26.
Изменение кинетической энергии точкина некотором перемещении равно сумме
работ всех действующих на нее сил на
этом же перемещении
26
Теорема об изменении энергии
27.
Запишем дифф. уравнение движения точкиma Fi .
i
Спроектируем его на тангенциальную ось
ma Fi .
i
Представим тангенциальное
ускорение в виде
dv dv ds
dv
a
v ,
dt ds dt
ds
и учтем, что проекция силы
Fi Fi cos .
dv
mv Fi cos .
ds
i
27
Теорема об изменении энергии
28.
Умножим обе части уравнения на элементарное перемещение ипроинтегрировав, получим
mvdv Fi cos ds,
i
mvdv F cos ds,
i
BC
mvC2 mvB2
Fi cos ds,
2
2
i BC
Теорема доказана
28
Теорема об изменении энергии
i
BC
29.
Аm
B
29
Теорема об изменении энергии
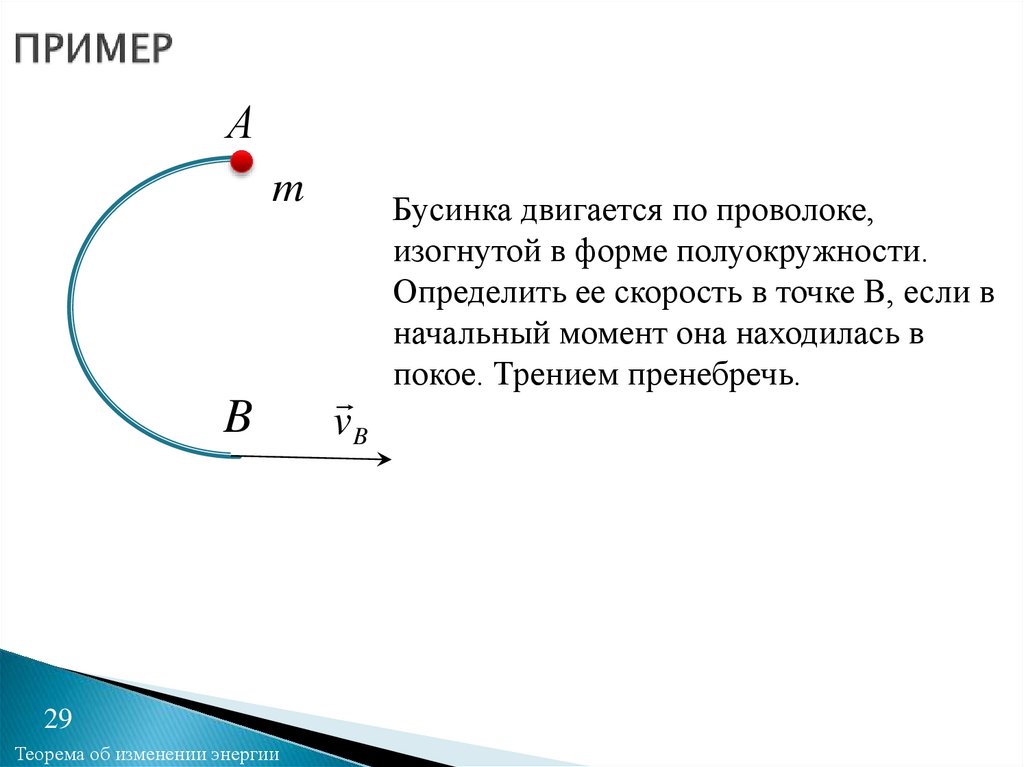
vB
Бусинка двигается по проволоке,
изогнутой в форме полуокружности.
Определить ее скорость в точке B, если в
начальный момент она находилась в
покое. Трением пренебречь.
30.
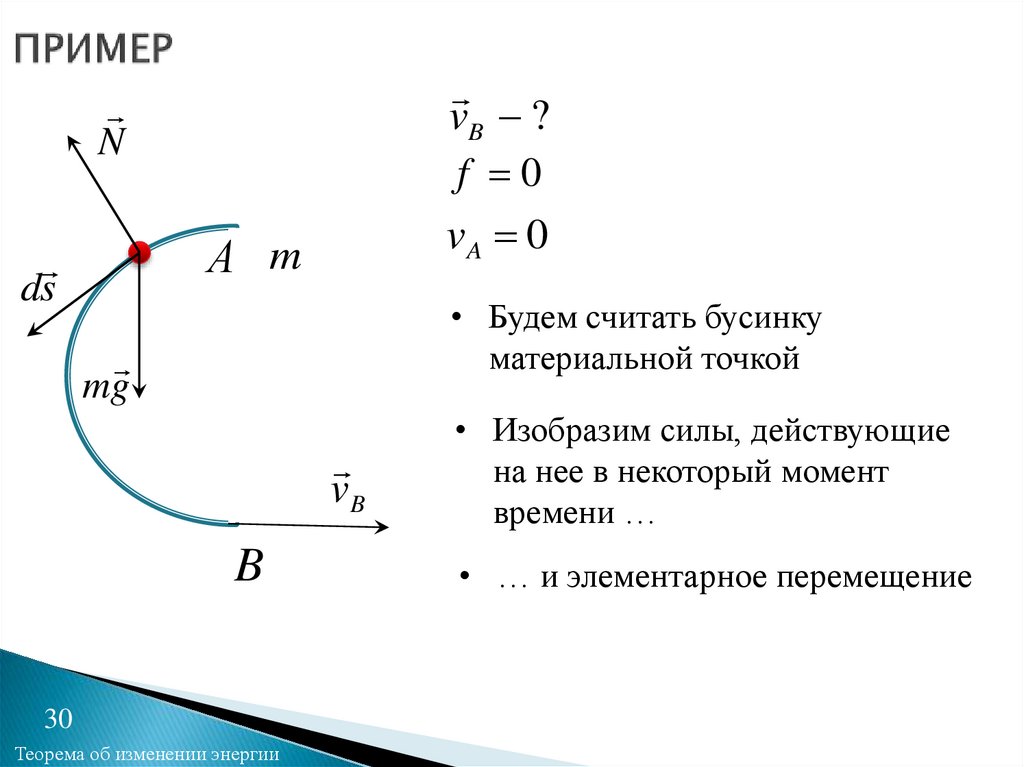
vB ?f 0
vA 0
N
А m
ds
• Будем считать бусинку
материальной точкой
mg
vB
B
30
Теорема об изменении энергии
• Изобразим силы, действующие
на нее в некоторый момент
времени …
• … и элементарное перемещение
31.
N• Запишем теорему об изменении
кинетической энергии
А
mvB2 mvA2
A( N ) A(mg )
2
2
A( N ) N cos ( / 2) ds 0
ds
mg
AB
vB
A(mg ) mg cos ( ) ds
AB
B
/2
ds R d
A(mg ) 2 mg sin ( ) R d 2mgR cos (0) 2mgR
0
31
Теорема об изменении энергии
32.
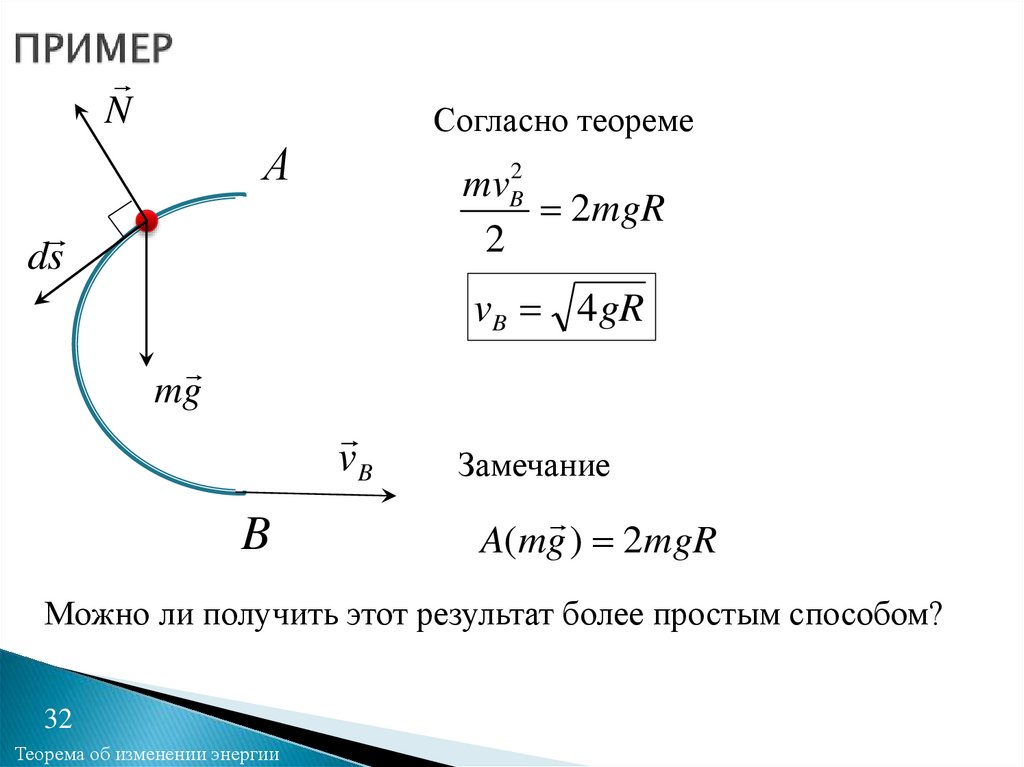
NСогласно теореме
А
mvB2
2mgR
2
ds
vB 4 gR
mg
vB
B
Замечание
A( mg ) 2mgR
Можно ли получить этот результат более простым способом?
32
Теорема об изменении энергии
33.
Градиентом называетсявектор с компонентами
/ x
/ y
/ z
Сила называется потенциальной
(консервативной), если ее можно
представить в виде градиента некоторой
скалярной функции, называемой
потенциалом
33
Теорема об изменении энергии
F
34.
Работа потенциальной силы не зависит отформы траектории точки и закона ее
движения и определяется только
начальным и конечным положением точки
F
i
j
k
x
y
z
B B
A( F ) F ds
i
j
k dxi dyj dzk
x
y
z
A
A
B
B
A( F )
dx
dy
dz d B A
x
y
z A
A
34
Теорема об изменении энергии
35.
zПопробуем построить потенциал
для силы тяжести
mg
y
x
0,
x
F
i
j
k
x
y
z
F mgk
0,
y
mg.
z
mgz
35
Теорема об изменении энергии
36.
ЗамечаниеПотенциал определяется с точностью до некоторой не зависящей
от координат постоянной
( C )
Потенциальной энергией точки, находящейся
под действием консервативной силы,
называется величина П
Пусть F
B
A( F ) F ds B A П А П B П
A
A( F ) П
36
Теорема об изменении энергии
37.
Запишем теорему об изменении кинетической энергии для точки,находящейся под действием потенциальной силы
Tк Tн A( F ) ( Пк Пн )
Tк Пк Пн Tн
Для точки, находящейся под действием
потенциальной силы, можно ввести полную
механическую энергию как сумму ее
потенциальной и кинетической энергий.
При движении точки она сохраняется.
Если на точку действует несколько потенциальных сил
37
Теорема об изменении импульса
П i
38.
zmgz С
h
П mgz С
mg
x
y
A(mg ) mgh
A( mg ) П
mgzн mgzк mg zн zк
k
A( Fупр ) lн2 lк2
2
38
Теорема об изменении энергии
39.
1. Какие из уравнений динамики точки записываются ввиде векторных уравнений, а какие – скалярных?
2. Что такое импульс материальной точки?
3. Как определяется импульс силы за конечный
промежуток времени?
4. При каких условиях количество движения системы не
изменяется?
5. Как определяется и момент количества движения точки?
6. Чему равна проекция момента количества движения
точки относительно центра на ось?
39
Заключение
40.
7. Как происходит движение материальной точки поддействием центральной силы? Как формулируется закон
Кеплера?
8. Как определяется работа постоянной силы на
прямолинейном перемещении точки, к которой она
приложена? А если сила переменная и точка
перемещается по кривой?
9. Что понимают под элементарной работой силы и как она
связана с работой силы на конечном перемещении точки,
к которой она приложена? Когда элементарная работа
равна нулю?
40
Заключение
41.
Динамика механическойсистемы
41
Заключение


































 physics
physics








