Прямоугольный треугольник

1. Прямоугольный треугольник

α
c
b
sin cos
a
c
cos sin
b
c
tg
sin
cos
ctg
a
b
Теорема Пифагора
900
β
a
c a b
2
2

2.

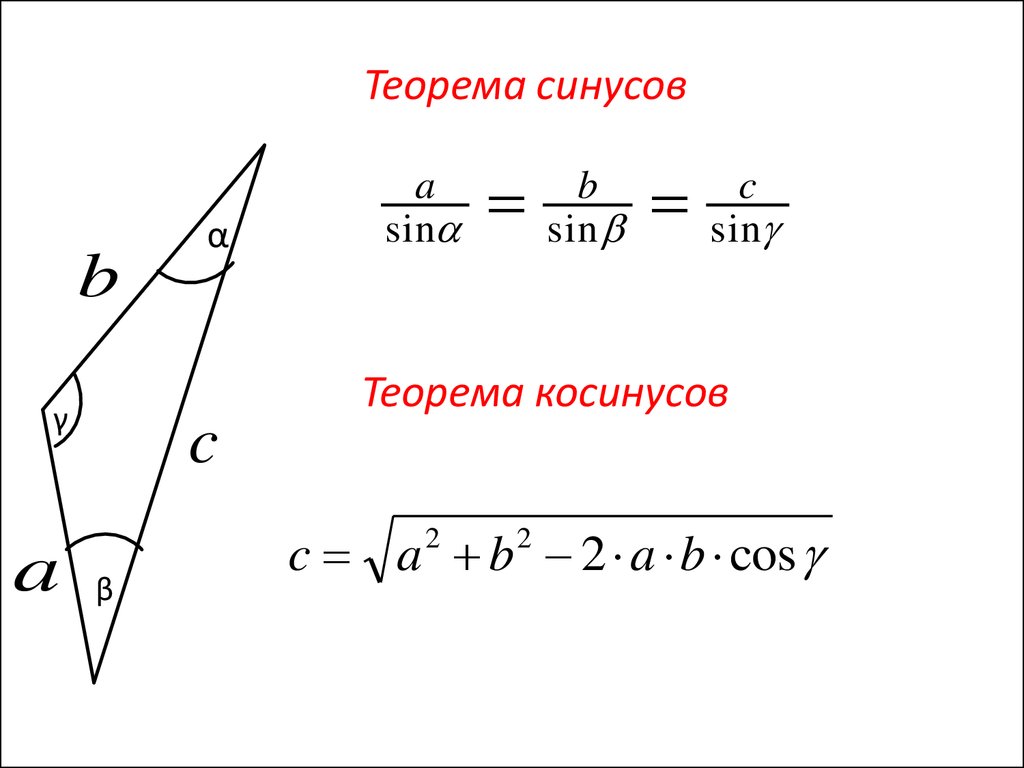
Теорема синусов
b
γ
a
α
c
a
sin
c
sin
Теорема косинусов
c a b 2 a b cos
2
β
b
sin
2

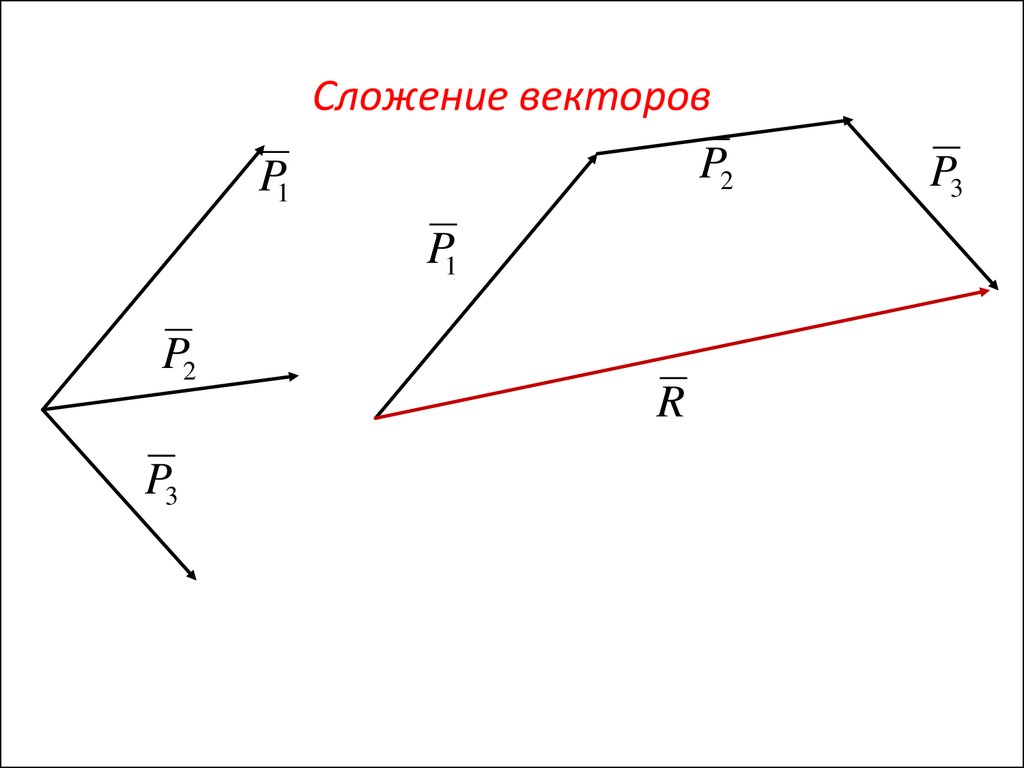
3. Сложение векторов

P2
P1
P1
P2
P3
R
P3

4. Теорема о 3-х силах Если тело находится в равновесии под действием 3-х сил и линии действия двух пересекаются, то линия действия 3-ей силы про

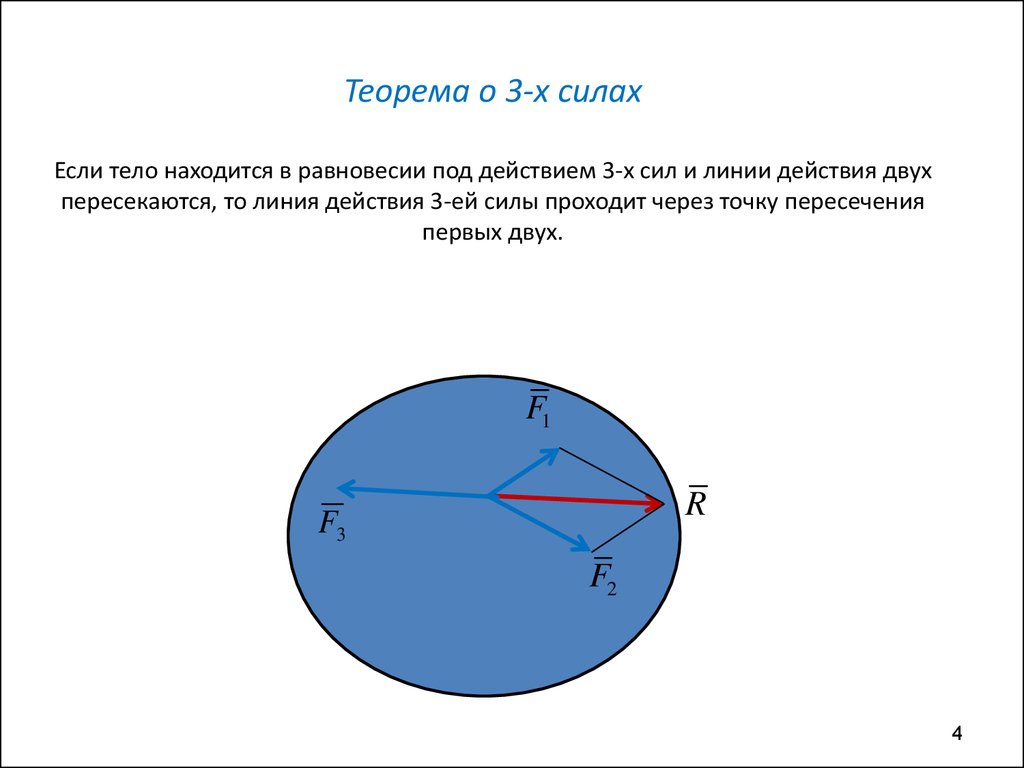
Теорема о 3-х силах
Если тело находится в равновесии под действием 3-х сил и линии действия двух
пересекаются, то линия действия 3-ей силы проходит через точку пересечения
первых двух.
F1
R
F3
F2
4

5.

Пример 2
Дано : Q 10н; АВ 2 м; АС 1м
Определить : RA ; RB
Аналитическое решение
y
А
F
F
О
Q
RB
RA
60
С
В
30
kx
0;
ky
0;
x
60
RA cos30 Q cos60 RB cos60 0;
RA sin30 Q sin60 RB sin60 0.
5

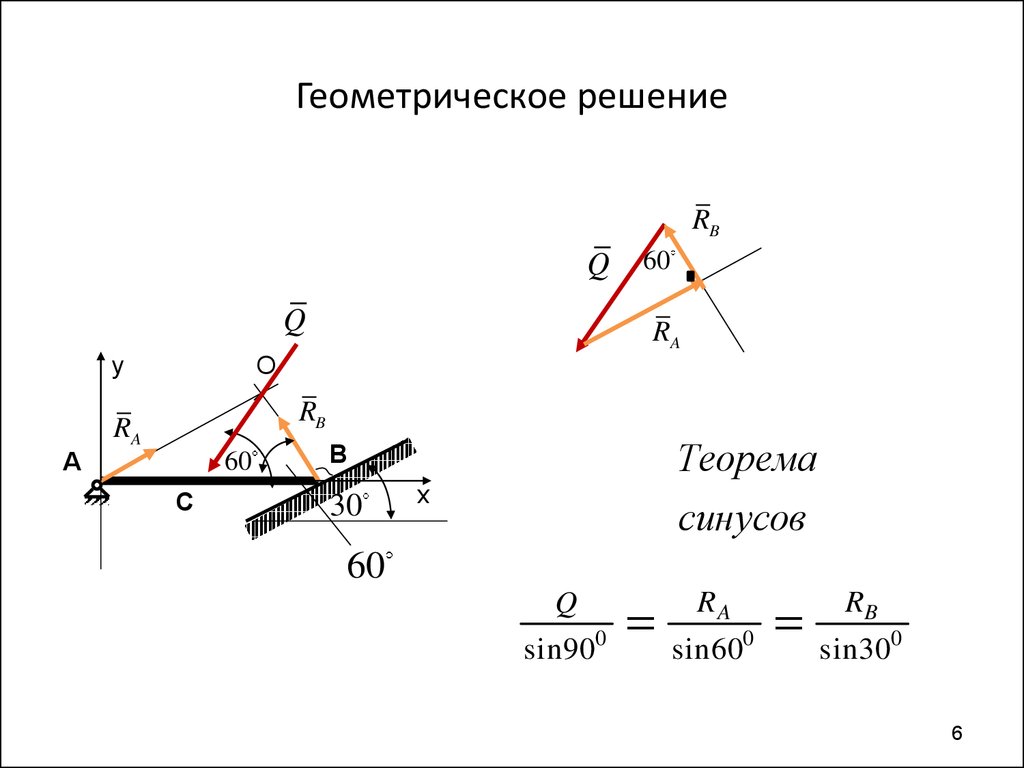
6. Геометрическое решение

RB
Q
Q
А
RA
О
y
60
RB
RA
60
С
Теорема
В
30
x
синусов
60
Q
0
sin 90
RA
0
sin 60
RB
sin 300
6

7.

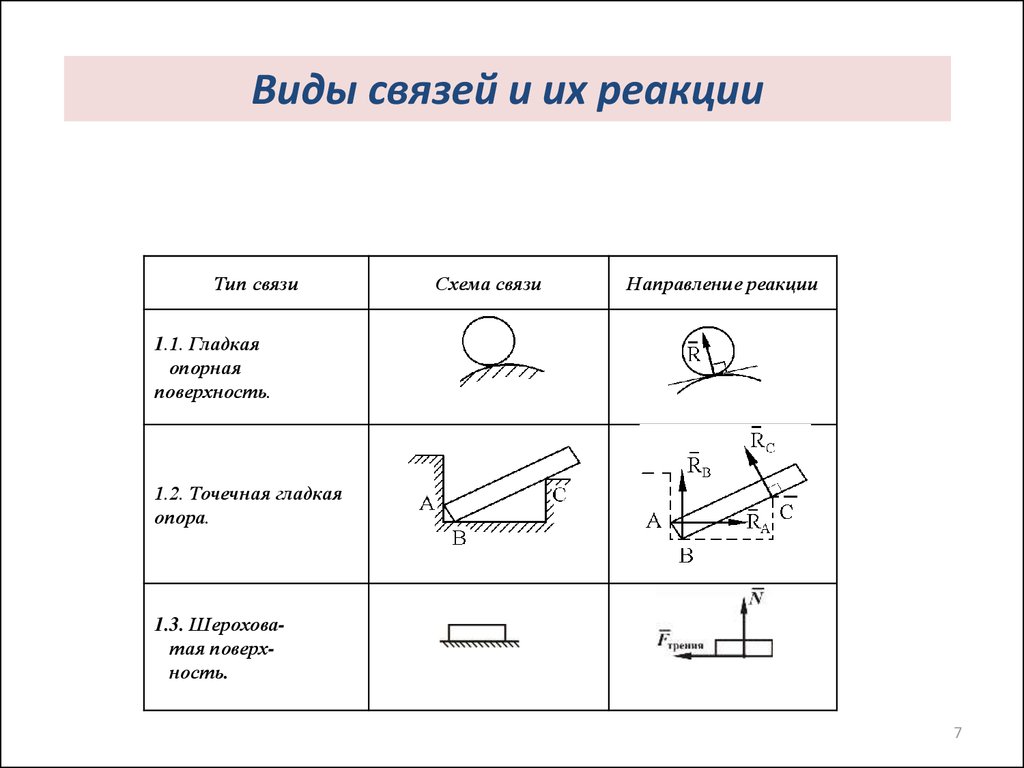
Виды связей и их реакции
Тип связи
Схема связи
Направление реакции
1.1. Гладкая
опорная
поверхность.
1.2. Точечная гладкая
опора.
1.3. Шероховатая поверхность.
7

8.

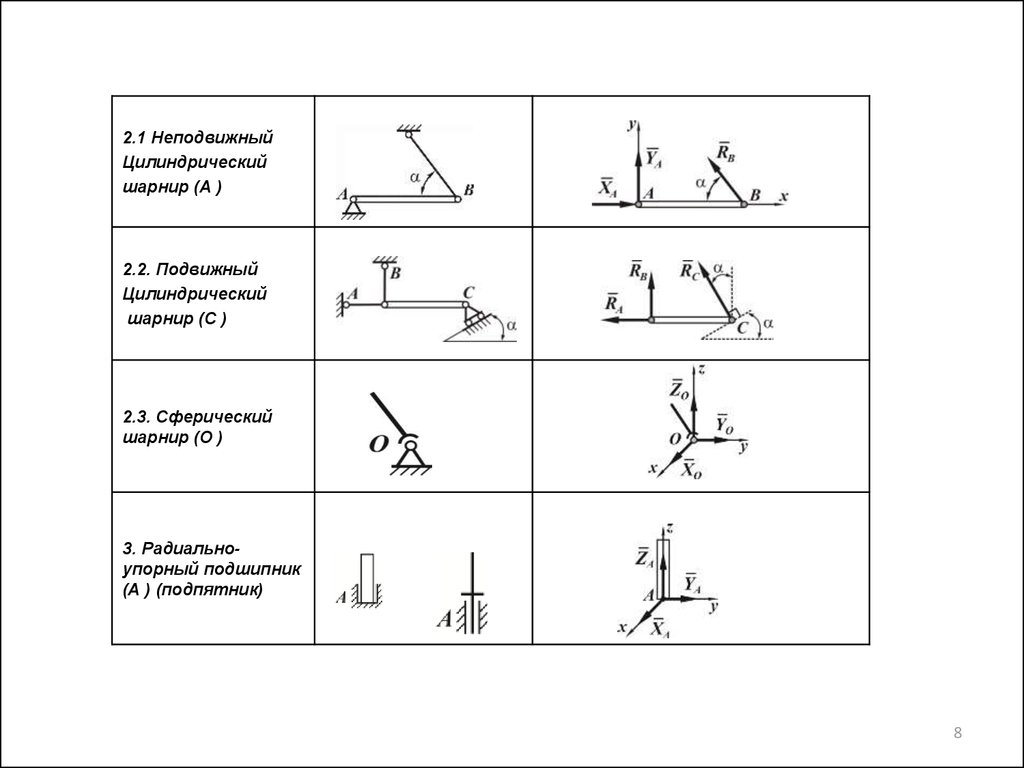
2.1 Неподвижный
Цилиндрический
шарнир (А )
2.2. Подвижный
Цилиндрический
шарнир (С )
2.3. Сферический
шарнир (О )
3. Радиальноупорный подшипник
(А ) (подпятник)
8

9.

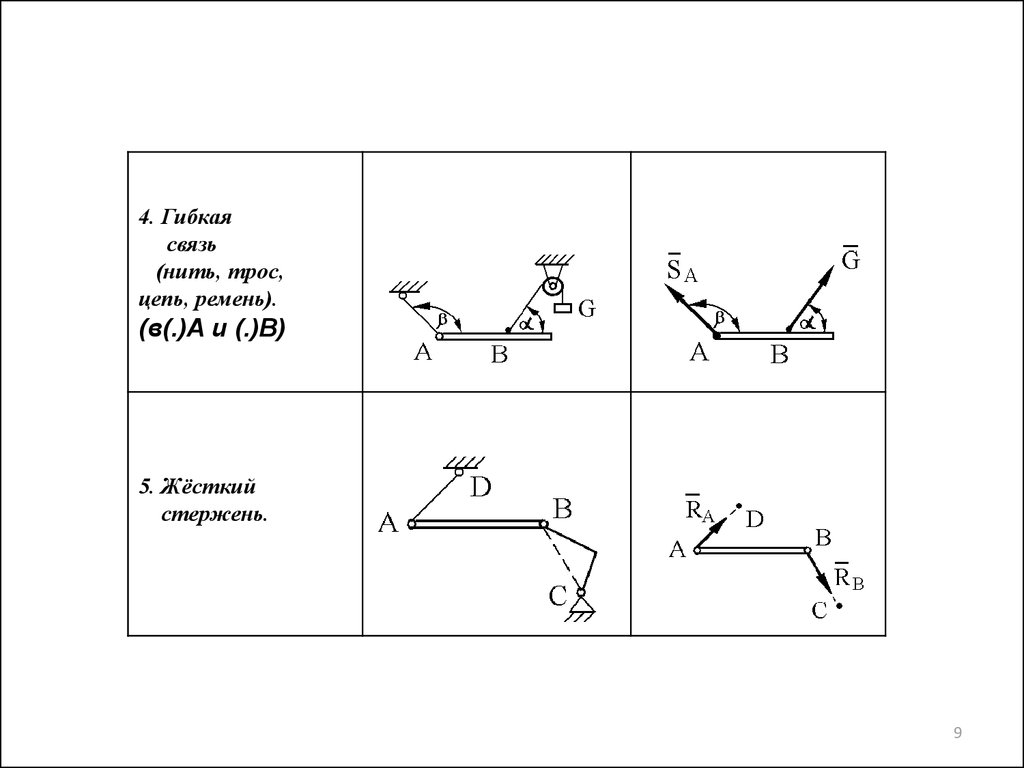
4. Гибкая
связь
(нить, трос,
цепь, ремень).
(в(.)А и (.)В)
5. Жёсткий
стержень.
9

10.

6.1. Жёсткая
заделка в
пространстве
6.2. Жёсткая
заделка в
плоскости
В
В
6.3. Скользящая заделка.
6.4. Свободная
заделка.
10

11.

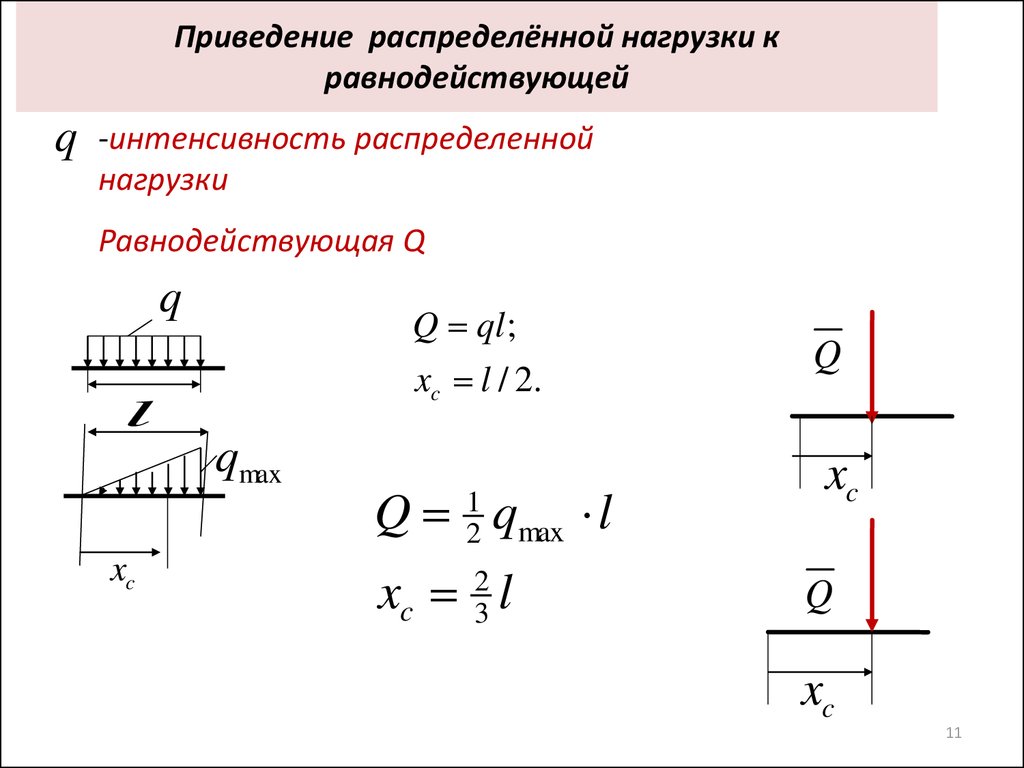
Приведение распределённой нагрузки к
равнодействующей
q
-интенсивность распределенной
нагрузки
Равнодействующая Q
q
Q ql ;
xc l / 2.
l
qmax
xc
Q 12 qmax l
xc 23 l
Q
xc
Q
xc
11

12.

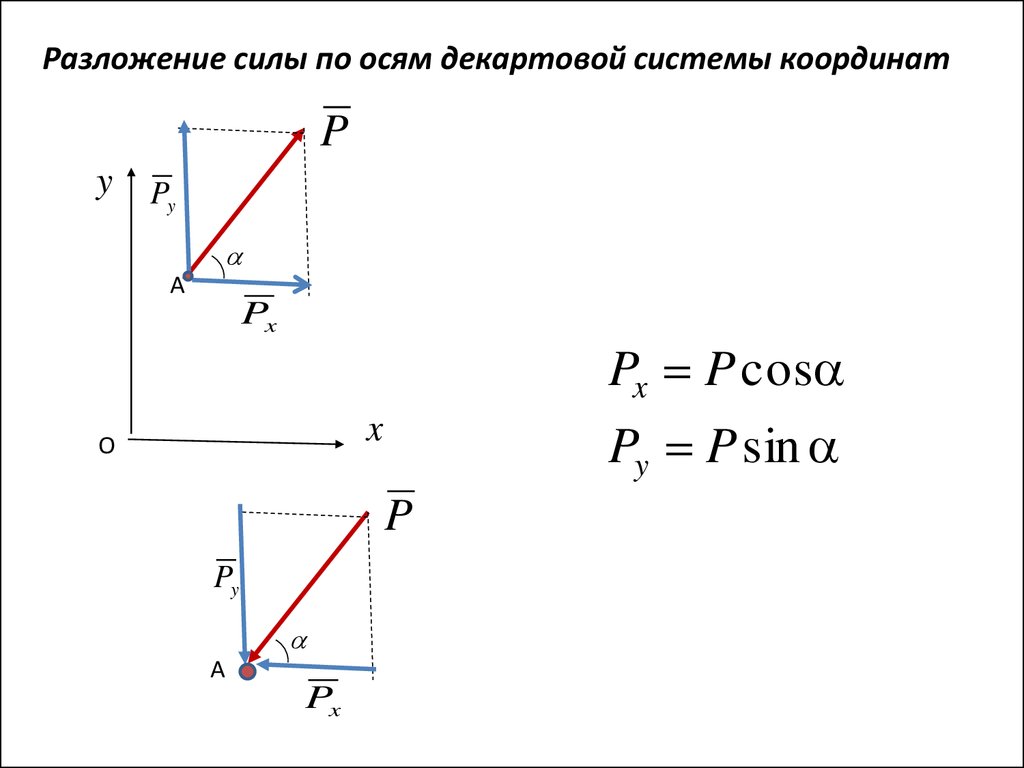
Разложение силы по осям декартовой системы координат
P
y P
y
А
Px
Px P cos
Py P sin
x
О
P
Py
А
Px

13.

1-я (основная) форма
уравнений равновесия
1. Fkx 0;
2-я форма уравнений равновесия
(прямая АВ не перпендикулярна оси OX)
1. Fkx 0;
2. Fky 0;
3. mA ( Fk ) 0.
2. mA ( F k ) 0; 3. mB ( F k ) 0.
3-я форма уравнений равновесия
(все три точки А,В,С не лежат на одной прямой)
1. mA ( F k ) 0; 2. mB ( F k ) 0; 3. mC ( F k ) 0.
Задача называется статически определимой, если число неизвестных
равно числу независимых уравнений равновесия.

14. Пример 1. Тело АВ находится в равновесии.

P 10н; q 10 мн ; m 10нм a 1м; 300
Px P sin 5н
P
α
А
q
m
Py P cos 5 3н
В
2a
Q q 2a 20н
2a
2a
Определить реакции глухой заделки
x B ; y B ; mB

15.

Составим расчетную схему
mB
Py
yB
xB
F
x
Q
m
Px
xB Px 5
В
2a
F
y
А
m
B
a
3a
xB Px 0
y B Q Py 0
y B Q Py 20 5 3
mB m Q 3a Py 4a Px 2a 0
mB m Q3a Py 4a Px 2a 10 60 20 3 10 20 3 40

16.

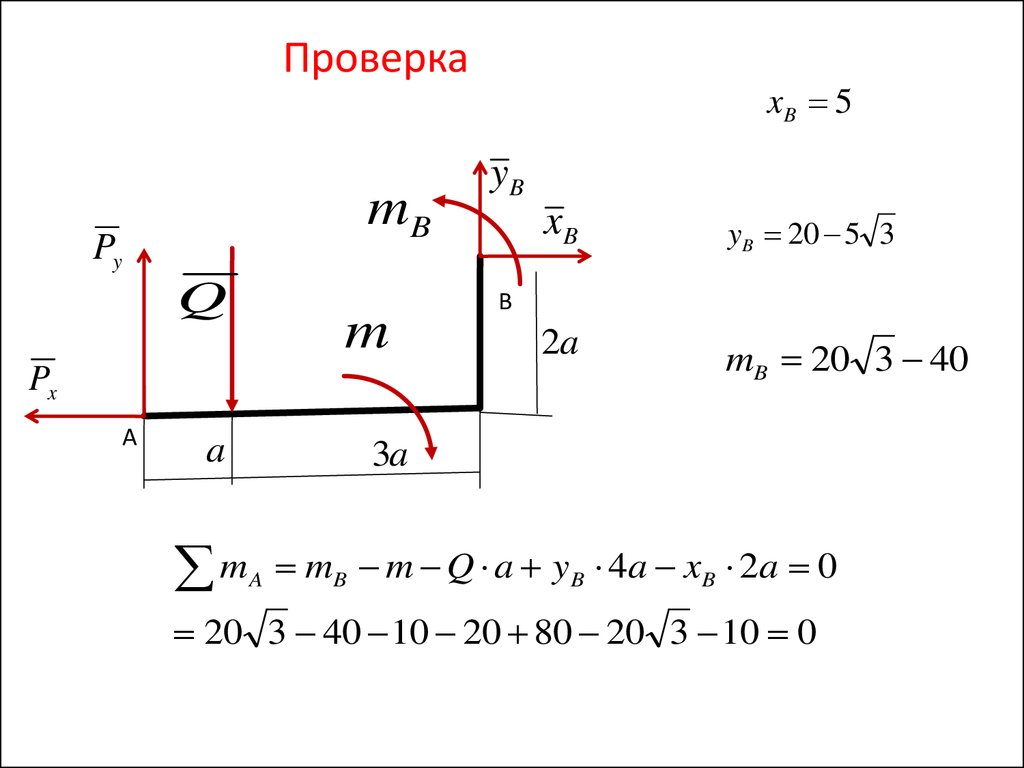
Проверка
mB
Py
Q
m
Px
А
a
m
xB 5
yB
xB
yB 20 5 3
2a
mB 20 3 40
В
3a
A
mB m Q a y B 4 a x B 2 a 0
20 3 40 10 20 80 20 3 10 0

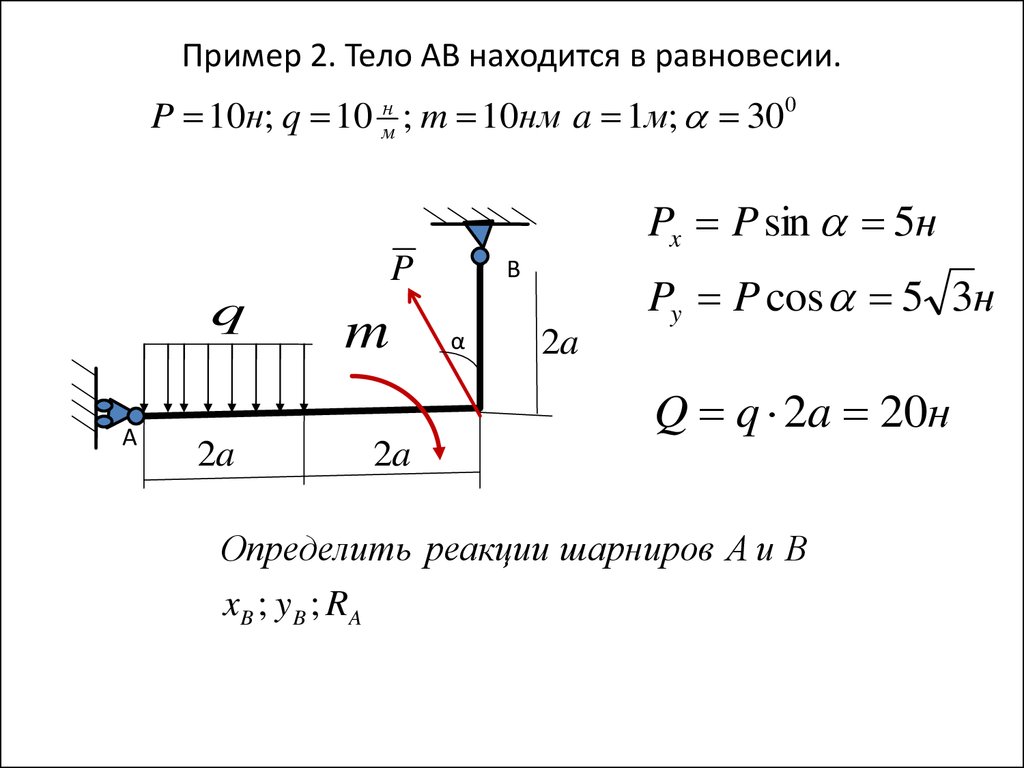
17. Пример 2. Тело АВ находится в равновесии.

P 10н; q 10 мн ; m 10нм a 1м; 300
Px P sin 5н
P
q
А
m
В
α
Py P cos 5 3н
2a
Q q 2a 20н
2a
2a
Определить реакции шарниров А и В
xB ; y B ; RA

18.

Составим расчетную схему
yB
xB
Py
Q
m
RA
А
a
Px
В
F
y
y B Q Py 20 5 3
2a Fx xB Px RA 0
xB Px RA 5 ( 20) 25
3a
m
B
m Q 3a Px 2a RA 2a 0
RA 2a m Q3a Px 2a
RA
y B Q Py 0
m Q 3a Px 2 a
2a
10 602 10 20

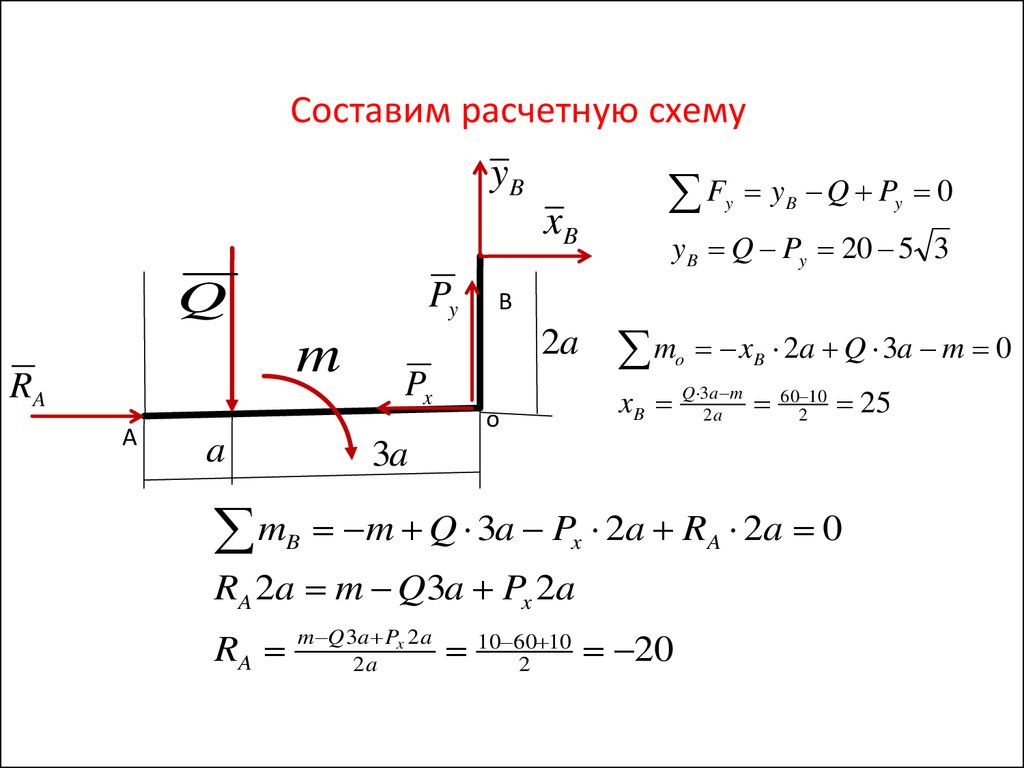
19.

Составим расчетную схему
yB
xB
Py
Q
m
RA
А
a
y
y B Q Py 20 5 3
о
m
o
xB
xB 2a Q 3a m 0
Q 3a m
2a
60 10
2
25
3a
m
B
m Q 3a Px 2a RA 2a 0
RA 2a m Q3a Px 2a
RA
y B Q Py 0
В
2a
Px
F
m Q 3a Px 2 a
2a
10 602 10 20

20.

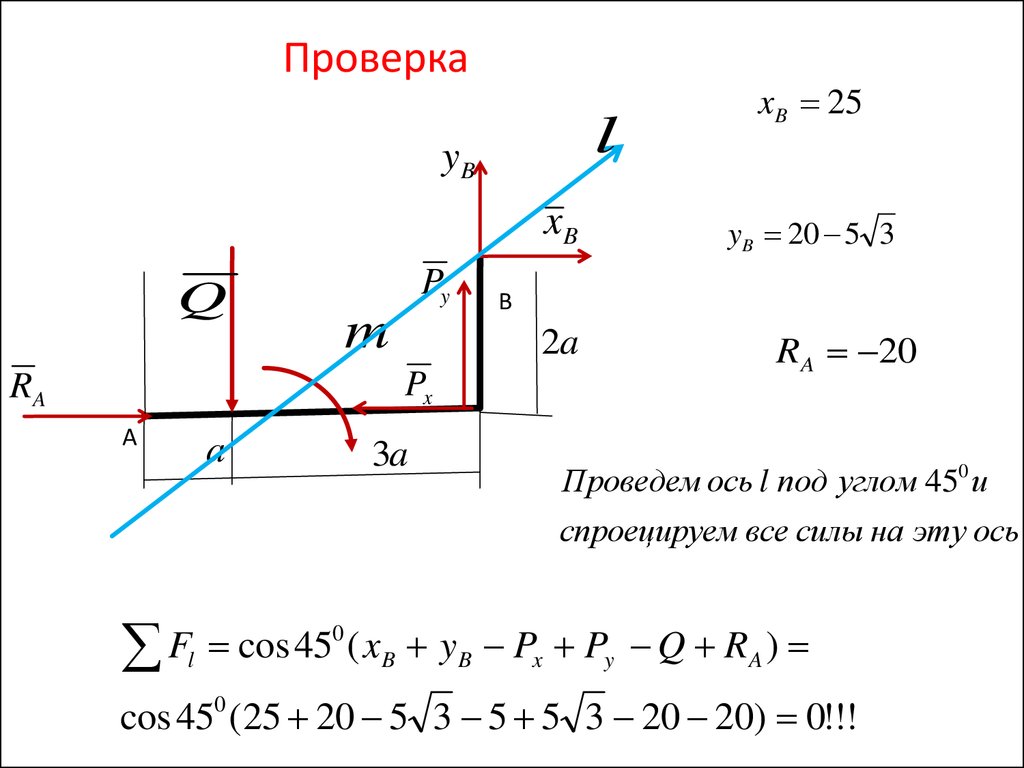
Проверка
l
yB
xB
Q
Py
m
А
a
3a
yB 20 5 3
В
2a
Px
RA
xB 25
RA 20
Проведем ось l под углом 450 и
спроецируем все силы на эту ось
0
F
cos
45
( xB y B Px Py Q RA )
l
cos 450 (25 20 5 3 5 5 3 20 20) 0!!!

21. Равновесие системы тел (составной конструкции)

Составной конструкцией называется система тел,
связанная внутренними связями.
Расчет составной конструкции - методом разделения конструкции
по внутренним связям.
Типы внутренних связей
1. Наложение
2. Стержень
3. Шарнир

22.

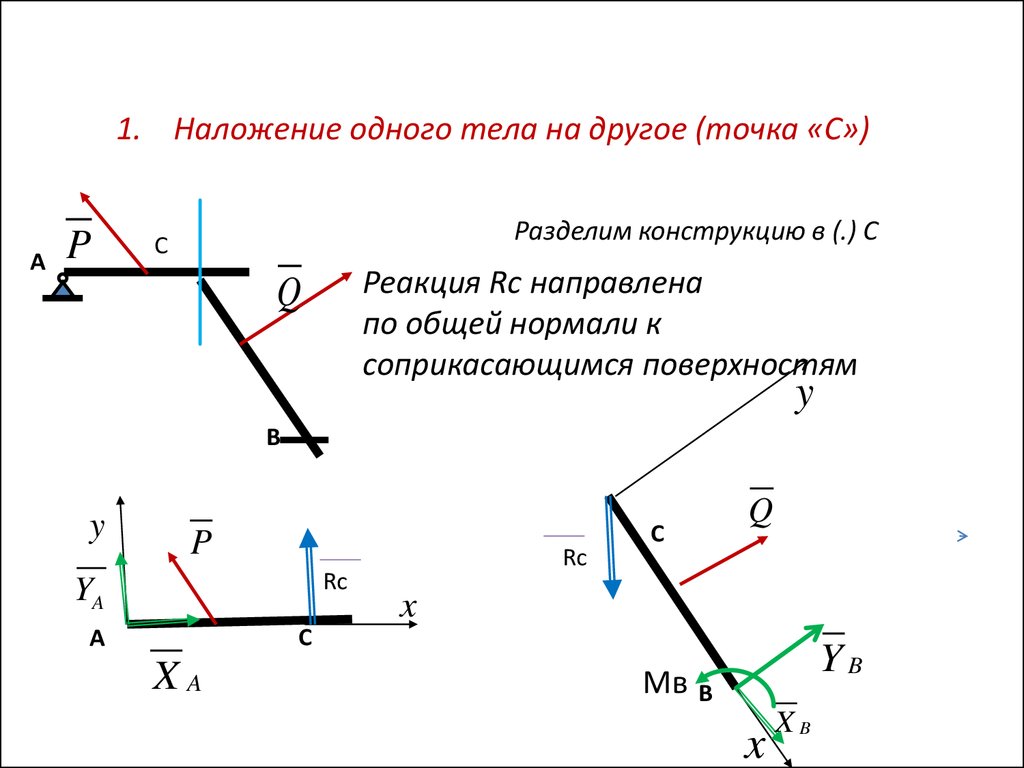
1. Наложение одного тела на другое (точка «С»)
А
P
Разделим конструкцию в (.) С
С
Реакция Rc направлена
по общей нормали к
соприкасающимся поверхностям
Q
y
В
y
P
Rc
YA
Rc
Q
С
x
С
А
XA
Мв
YB
В
x
XB

23.

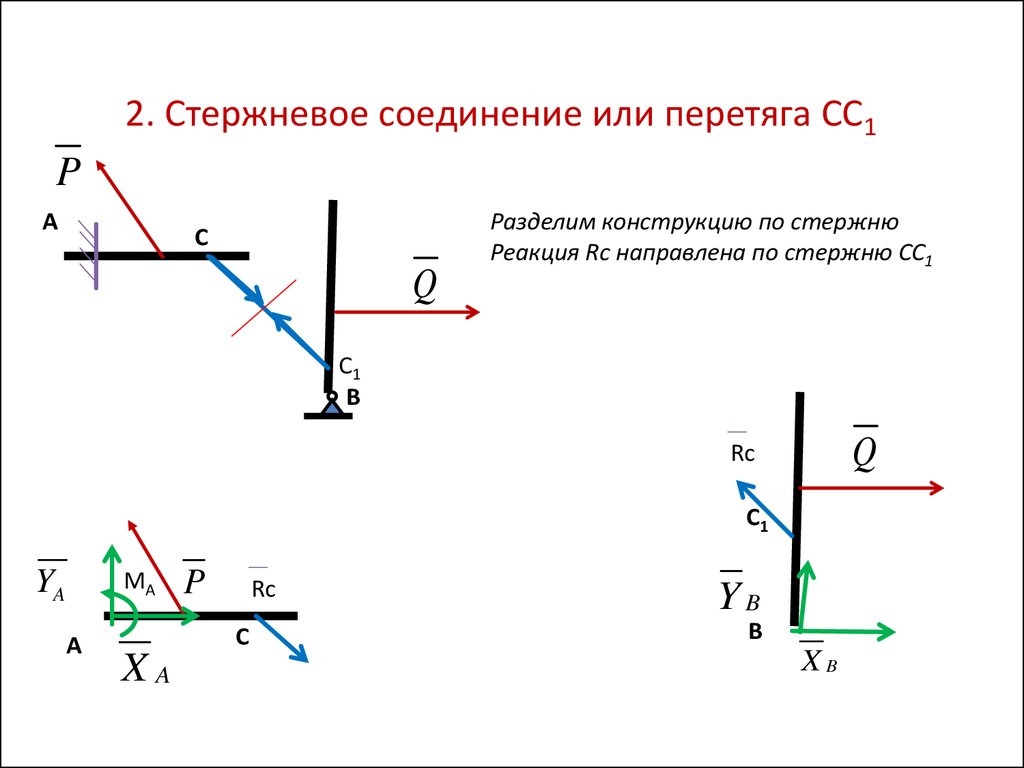
2. Стержневое соединение или перетяга СС1
P
А
С
Q
Разделим конструкцию по стержню
Реакция Rс направлена по стержню СС1
С1
В
Q
Rc
С1
YA
МА
А
P
Rc
С
XA
YB
В
XB

24.

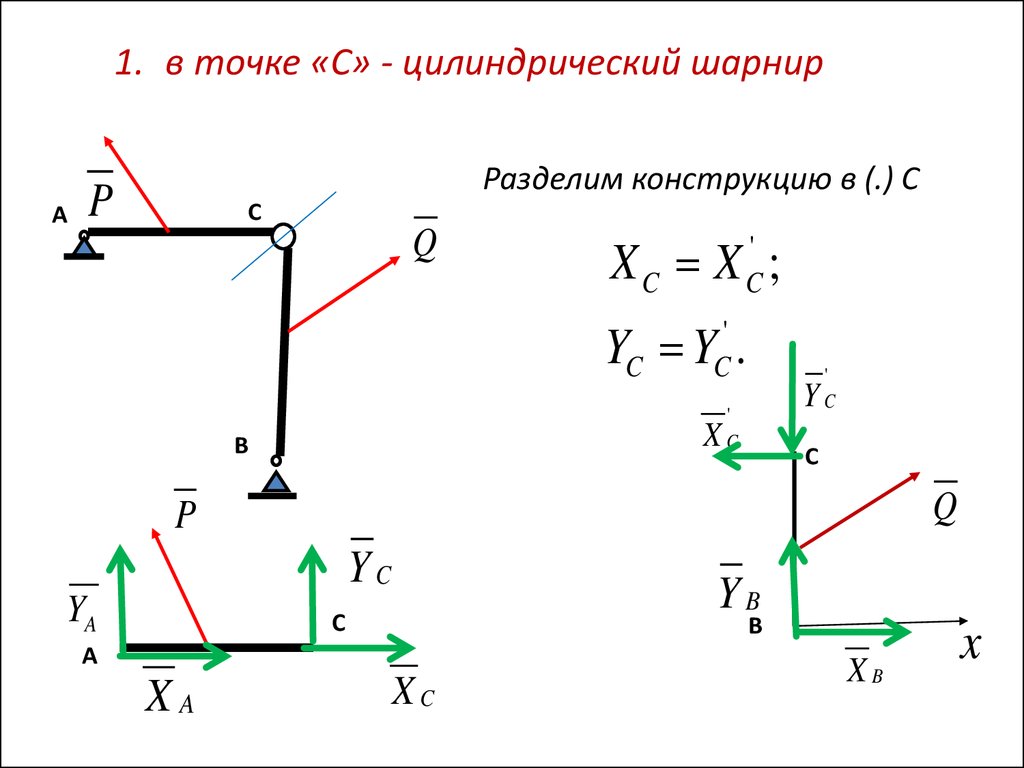
1. в точке «С» - цилиндрический шарнир
А
Разделим конструкцию в (.) С
P
С
Q
XC X ;
'
C
YC Y .
'
C
X
В
Y
'
C
'
C
С
Q
P
YC
YA
YB
С
В
А
XA
XC
XB
x

25.

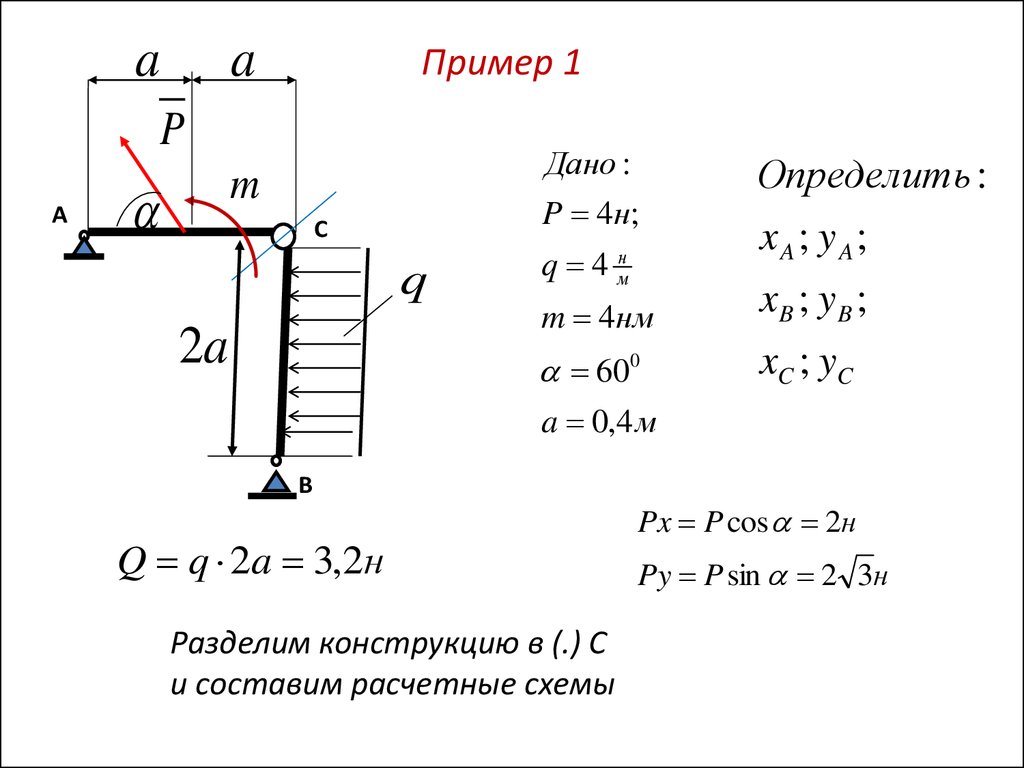
a
a
Пример 1
P
А
Дано :
P 4н;
m
С
q
2a
q 4 мн
Определить :
xA ; y A ;
m 4нм
xB ; y B ;
600
xC ; yC
a 0,4 м
В
Q q 2a 3,2н
Разделим конструкцию в (.) С
и составим расчетные схемы
Px P cos 2н
Py P sin 2 3н

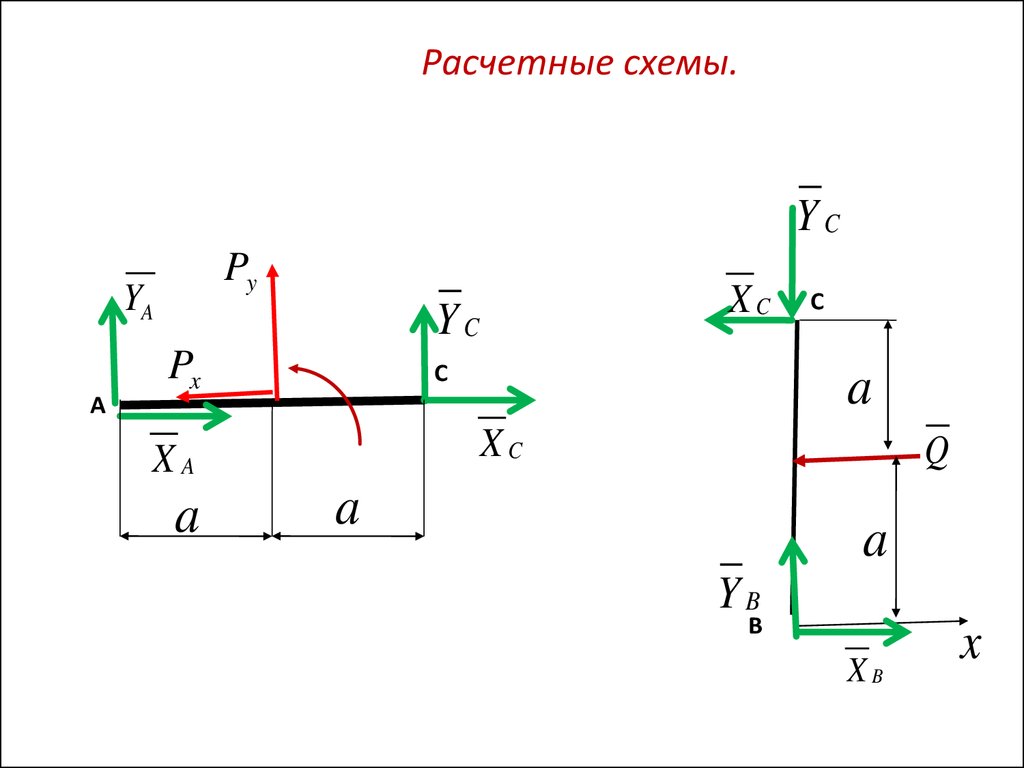
26.

Расчетные схемы.
YC
Py
YA
А
XC
YC
Px
С
a
XC
XA
a
С
Q
a
a
YB
В
XB
x

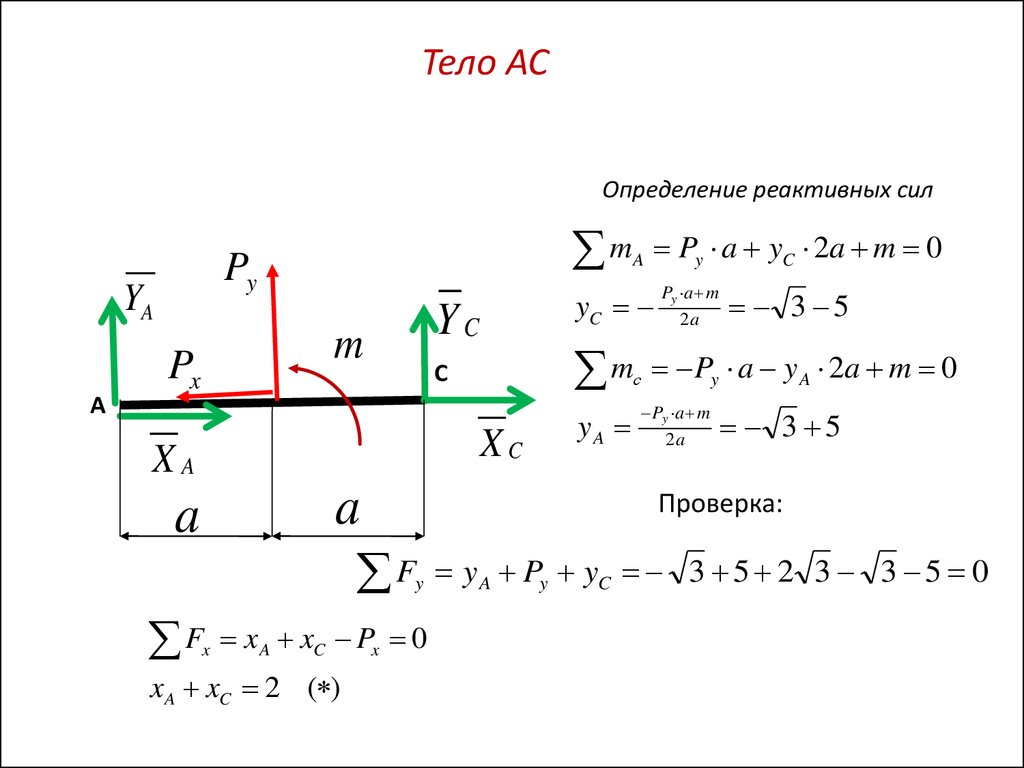
27.

Тело АС
Определение реактивных сил
Py
YA
А
m
Px
m
С
с
XC
XA
a
a
y
x
x A xC Px 0
x A xC 2 ( )
yA
Py a m
2a
3 5
Py a y A 2a m 0
Py a m
2a
3 5
Проверка:
F
F
Py a yC 2a m 0
yC
YC
m
A
y A Py yC 3 5 2 3 3 5 0

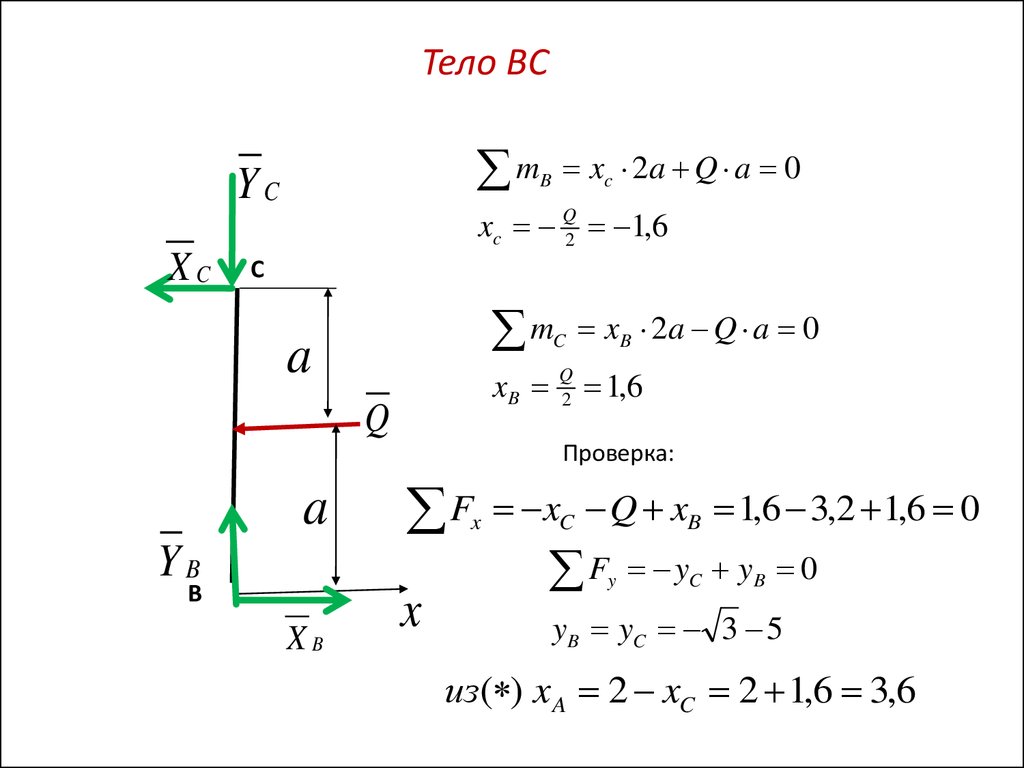
28.

Тело ВС
m
YC
XC
xc 2a Q a 0
B
xc Q2 1,6
С
m
C
a
xB
Q
Q
2
x B 2a Q a 0
1,6
Проверка:
a
F
x
YB
xC Q xB 1,6 3,2 1,6 0
F
y
В
XB
x
yC yB 0
yB yC 3 5
из( ) x A 2 xC 2 1,6 3,6

29.

Проверка для всей конструкции.
Py
YA
А
Px
l
m
x A 3,6н
С
XA
a
Ответ :
y A ( 3 5)н
xB 1,6н
a
a
y B ( 3 5)н
Q
xC 1,6н
a
yС ( 3 5) н
YB
В
XB
x
Проведем ось l
0
F
cos
45
( y A x A Py Px Q y B xB )
l
3 5 3,6 2 3 2 3,2 3 5 1,6 0