Печайтис2

1. Неравенство треугольника

Выполнил: студент 5 курса 5
группы ФМФ Печайтис Кирилл
Брянск 2009

2.

Геометрию интересуют соотношения между элементами фигур.
Какие соотношения между элементами
треугольника нам уже известны?
В
В треугольнике: против большей стороны лежит
больший угол; против большего угла лежит
большая сторона
А
С
Есть ли соотношение только между сторонами треугольника?
Определите на моделях трех отрезков, всегда ли из них можно
сложить треугольник
Почему не всегда можно сложить треугольник из трех отрезков,
помогает выяснить следующая теорема

3. Работа с формулировкой теоремы. Теорема: Каждая сторона треугольника меньше суммы двух других сторон

О какой фигуре идет речь в теореме?
В
О каких элементах идет речь?
Что требуется доказать в теореме?
А
С
Дано: ABC треугольник
AB, AC, CB - стороны
Доказать: AB < AC + CB
Какую сторону можно выбрать для
доказательства?
Любую

4.

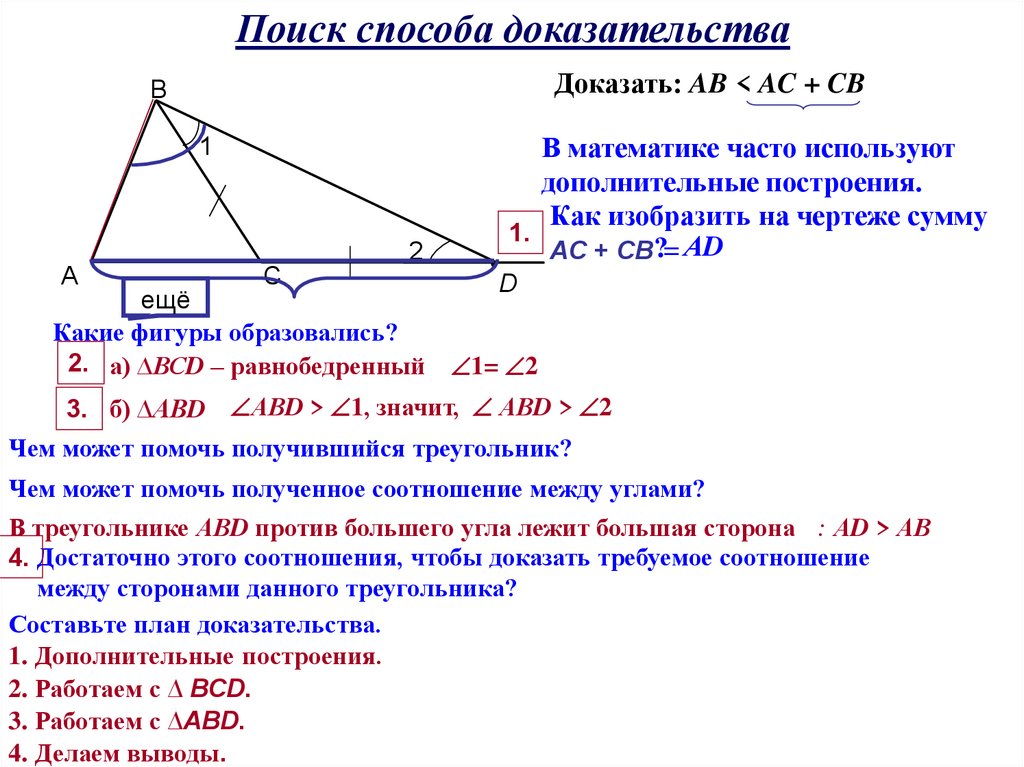
Поиск способа доказательства
Доказать: AB < AC + CB
В
1
А
С
2
ещё
Какие фигуры образовались?
2. а) ∆ВСD – равнобедренный
В математике часто используют
дополнительные построения.
Как изобразить на чертеже сумму
1.
AC + CB?= АD
D
1= 2
3. б) ∆АВD АВD > 1, значит, АВD > 2
Чем может помочь получившийся треугольник?
Чем может помочь полученное соотношение между углами?
В треугольнике АВD против большего угла лежит большая сторона : АD > АВ
4. Достаточно этого соотношения, чтобы доказать требуемое соотношение
между сторонами данного треугольника?
Составьте план доказательства.
1. Дополнительные построения.
2. Работаем с ∆ ВСD.
3. Работаем с ∆АВD.
4. Делаем выводы.

5.

Работа по учебнику с доказательством
Изучите доказательство, предложенное в школьном учебнике
Рассмотрим произвольный треугольник АВС и
Доказательство:
докажем, что АВ < AC + CB.
В
1
1
Отложим на продолжении стороны АС отрезок
СD, равный стороне СВ.
2
А
2
3
4
С
D
В равнобедренном треугольнике ВСD 1= 2,
а в треугольнике АВD АВD > 1, значит, АВD > 2. Так как в треугольнике против
большего угла лежит большая сторона, то АВ < АD.
Но АD = АС + СD = АС + СВ, поэтому АВ < АС + СВ.
Теорема доказана.
Выделите основные этапы доказательства.
Назовите приемы, используемые при доказательстве теоремы.
При доказательстве теоремы использовали: дополнительное построение
(строили сумму отрезков); рассматривали образовавшиеся фигуры.

6.

Оформите доказательство
В
1
2
D
А
С
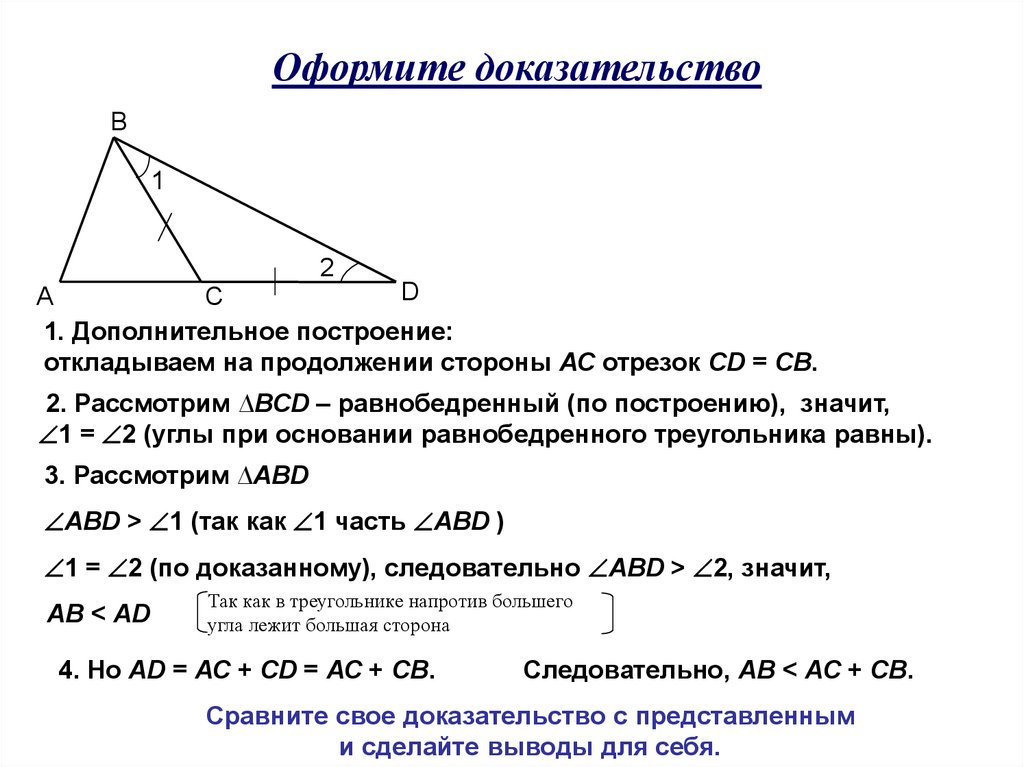
1. Дополнительное построение:
откладываем на продолжении стороны АС отрезок СD = СВ.
2. Рассмотрим ∆ВСD – равнобедренный (по построению), значит,
1 = 2 (углы при основании равнобедренного треугольника равны).
3. Рассмотрим ∆АВD
АВD > 1 (так как 1 часть АВD )
1 = 2 (по доказанному), следовательно АВD > 2, значит,
АВ < АD
Так как в треугольнике напротив большего
угла лежит большая сторона
4. Но АD = АС + СD = АС + СВ.
Следовательно, АВ < АС + СВ.
Сравните свое доказательство с представленным
и сделайте выводы для себя.

7.

Итоги работы с теоремой
С каким фактом познакомились?
Каждая сторона треугольника меньше суммы двух других сторон.
Какую фигуру характеризует данный факт? Треугольник.
Можно ли назвать данную теорему свойством треугольника?
Да, так как треугольник дан по условию теоремы.
Почему не всегда можно сложить треугольник из трех отрезков?
Так как сумма двух отрезков может оказаться меньше или равной третьему
отрезку, значит, эти отрезки не могут быть сторонами треугольника.
Что полезно запомнить из работы с теоремой?
1) Если дана сумма отрезков, то для построения этой суммы один из отрезков
удлиняют на величину второго отрезка.
2) Как только выполнили дополнительное построение, рассматривают
образовавшиеся фигуры.
3) При изучении доказательства, предложенного в учебнике, полезно
выделять этапы доказательства и используемые в нем приемы.
4) При оформлении доказательства, нужно выделять логично этапы
доказательства, обосновывать выводы.