Similar presentations:
Поверхности и тела. Инженерная и компьютерная графика. Лекция 3
1.
Инженерная и компьютерная графика.Лекция 3.
Поверхности и тела
Кайчёнов Александр Вячеславович,
заведующий кафедрой автоматики и вычислительной техники ФГАОУ «МАУ»
МУРМАНСКИЙ А
МРУКРТ И
МЧАЕН
СК
СИ
КЙ У Н И В Е Р С И Т Е Т
2024
2.
ПОВЕРХНОСТИ И ТЕЛАПоверхность – совокупность последовательных
положений некоторых перемещающихся в
пространстве линий
Тело - часть пространства, ограниченная со всех
сторон поверхностью
Геометрические поверхности могут быть образованы движением
в пространстве прямой или кривой линии, которая называется
образующей по заданной траектории, называемой направляющей.
В зависимости от формы образующей поверхности делятся на
линейчатые, когда образующей служит прямая линия, и
нелинейчатые, когда образующей служит кривая линия.
По закону движения образующих можем иметь поверхности с
поступательным движением, с вращательным движением –
поверхности вращения, и с винтовым движением – винтовые
поверхности.
МУРМАНСКИЙ АРКТИЧЕСКИЙ УНИВЕРСИТЕТ
По признаку направляющих, которые могут быть ломаными,
прямыми или кривыми, поверхности могут быть гранными
или кривыми.
2
3.
Проецирование геометрических тел.Проецирование многогранников
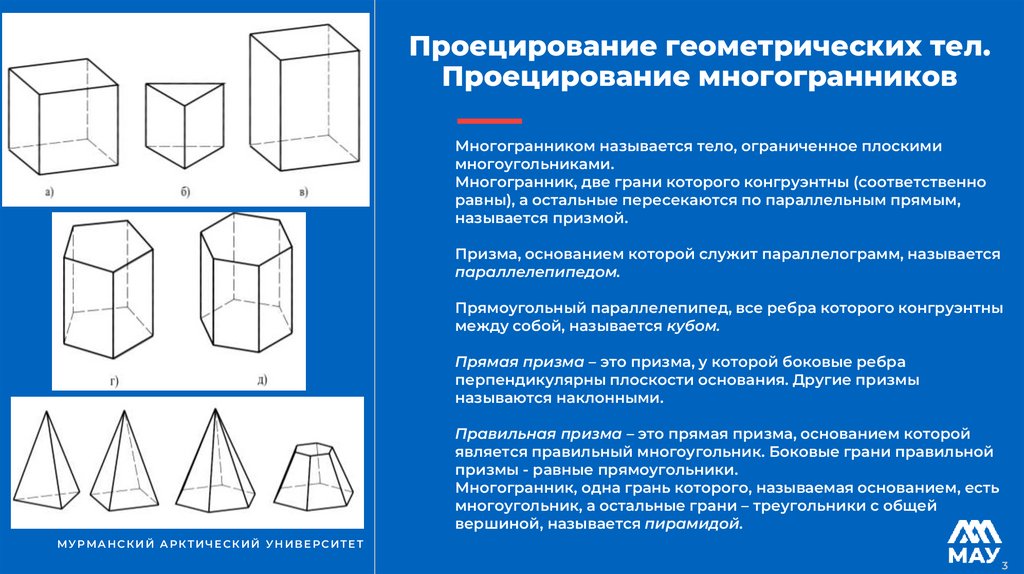
Многогранником называется тело, ограниченное плоскими
многоугольниками.
Многогранник, две грани которого конгруэнтны (соответственно
равны), а остальные пересекаются по параллельным прямым,
называется призмой.
Призма, основанием которой служит параллелограмм, называется
параллелепипедом.
Прямоугольный параллелепипед, все ребра которого конгруэнтны
между собой, называется кубом.
Прямая призма – это призма, у которой боковые ребра
перпендикулярны плоскости основания. Другие призмы
называются наклонными.
Правильная призма – это прямая призма, основанием которой
является правильный многоугольник. Боковые грани правильной
призмы - равные прямоугольники.
Многогранник, одна грань которого, называемая основанием, есть
многоугольник, а остальные грани – треугольники с общей
вершиной, называется пирамидой.
МУРМАНСКИЙ АРКТИЧЕСКИЙ УНИВЕРСИТЕТ
3
4.
Проецирование геометрических тел.Проецирование многогранников
Многогранник, у которого все грани за исключением одной
являются треугольниками с общей вершиной, называется
пирамидой. Треугольники называют боковыми гранями, а
оставшуюся грань – основанием пирамиды. Если основание – nугольник, то пирамиду называют n-угольной.
Треугольную пирамиду еще называют тетраэдром, а тетраэдр, у
которого все ребра равны, – правильным тетраэдром.
Ребра пирамиды, не принадлежащие основанию, называют
боковыми ребрами, а их общую точку – вершиной пирамиды.
Другие ребра и вершины обычно называют сторонами и
вершинами основания пирамиды.
Пирамиду называют правильной, если все ее боковые ребра равны
и в основании лежит правильный многоугольник.
МУРМАНСКИЙ АРКТИЧЕСКИЙ УНИВЕРСИТЕТ
Расстояние от вершины пирамиды до плоскости основания
называется ее высотой, часто под высотой пирамиды также
понимают отрезок, перпендикулярный основанию и имеющий
концы в вершине пирамиды и на плоскости основания.
Часть пирамиды, заключенная между плоскостью основания и
плоскостью, проведенной параллельно основанию с
пересечением боковых ребер пирамиды, называют
усеченной пирамидой
4
5.
Проецирование тел вращенияКривые линии принято рассматривать как линии
пересечения поверхностей или как траекторию k
непрерывно движущейся точки А. Сама линия также
называется непрерывной.
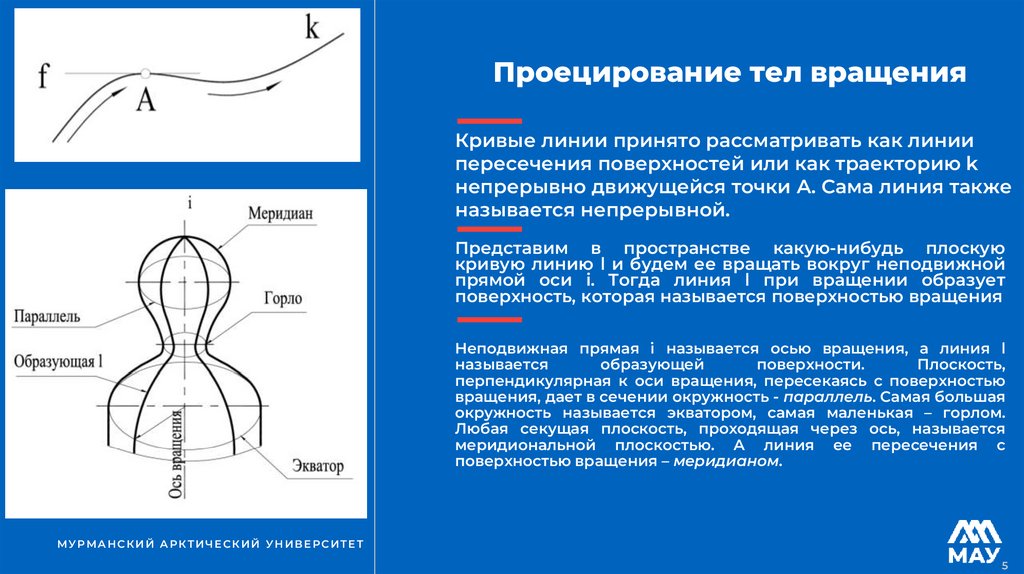
Представим в пространстве какую-нибудь плоскую
кривую линию l и будем ее вращать вокруг неподвижной
прямой оси i. Тогда линия l при вращении образует
поверхность, которая называется поверхностью вращения
Неподвижная прямая i называется осью вращения, а линия l
называется
образующей
поверхности.
Плоскость,
перпендикулярная к оси вращения, пересекаясь с поверхностью
вращения, дает в сечении окружность - параллель. Самая большая
окружность называется экватором, самая маленькая – горлом.
Любая секущая плоскость, проходящая через ось, называется
меридиональной плоскостью. А линия ее пересечения с
поверхностью вращения – меридианом.
МУРМАНСКИЙ АРКТИЧЕСКИЙ УНИВЕРСИТЕТ
5
6.
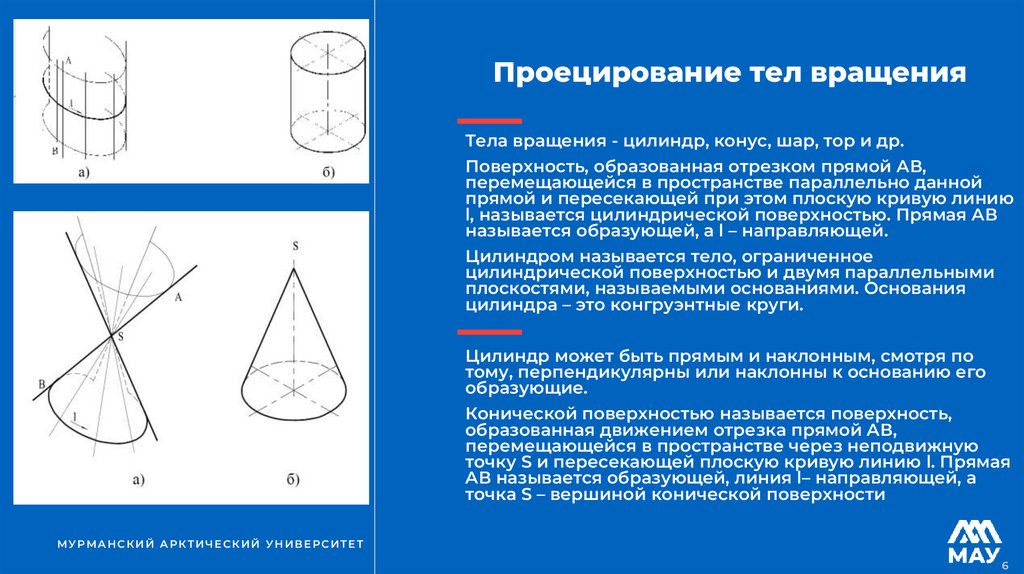
Проецирование тел вращенияТела вращения - цилиндр, конус, шар, тор и др.
Поверхность, образованная отрезком прямой АВ,
перемещающейся в пространстве параллельно данной
прямой и пересекающей при этом плоскую кривую линию
l, называется цилиндрической поверхностью. Прямая АВ
называется образующей, а l – направляющей.
Цилиндром называется тело, ограниченное
цилиндрической поверхностью и двумя параллельными
плоскостями, называемыми основаниями. Основания
цилиндра – это конгруэнтные круги.
Цилиндр может быть прямым и наклонным, смотря по
тому, перпендикулярны или наклонны к основанию его
образующие.
Конической поверхностью называется поверхность,
образованная движением отрезка прямой АВ,
перемещающейся в пространстве через неподвижную
точку S и пересекающей плоскую кривую линию l. Прямая
АВ называется образующей, линия l– направляющей, а
точка S – вершиной конической поверхности
МУРМАНСКИЙ АРКТИЧЕСКИЙ УНИВЕРСИТЕТ
6
7.
Проецирование тел вращенияПрямым круговым цилиндром называется тело, в
основаниях которого лежат круги, а ось вращения
перпендикулярна основаниям.
Отрезки, соединяющие соответствующие точки
окружностей кругов, называются образующими цилиндра.
Также можно сказать, что прямым круговым цилиндром
называется тело, образованное вращением
прямоугольника вокруг своей стороны.
Прямым круговым конусом называется тело,
ограниченное конической поверхностью, расположенной
по одну сторону от вершины, и плоскостью в виде круга,
перпендикулярной оси вращения, которая будет
называться основанием конуса.
Часть конической поверхности, от вершины до основания,
называется боковой поверхностью конуса, часть
образующей от вершины до основания называется
образующей конуса.
МУРМАНСКИЙ АРКТИЧЕСКИЙ УНИВЕРСИТЕТ
7
8.
Проецирование тел вращенияСферой называется поверхность, образованная
множеством точек пространства, находящихся на равном
расстоянии от данной точки. Сфера может быть
образована вращением окружности вокруг одного из
диаметров. Центр вращающейся окружности служит
центром сферы.
Тор образуется вращением окружности вокруг оси,
лежащей в плоскости окружности, но не проходящей
через ее центр. В случае, когда ось находится вне
окружности, получается открытый тор – кольцо.
МУРМАНСКИЙ АРКТИЧЕСКИЙ УНИВЕРСИТЕТ
8
9.
Изучитьсамостоятельно:
Благодарю за внимание!
Кайчёнов Александр Вячеславович
Заведующий кафедрой автоматики и
вычислительной техники ФГАОУ «МАУ
Тел: +7 (815) 2 40 33 78
Построение линий
пересечения поверхностей
плоскостью (Пересечение
поверхности плоскостью.pdf)
Примеры решений задач на
пересечение
поверхностей.pdf
mail: kaychenovav@mstu.edu.ru
https://www.mauniver.ru/structure/kafs/kaf_aivt/
Обобщенные позиционные
задачи на пересечение
поверхностей.pdf
МУРМАНСКИЙ АРКТИЧЕСКИЙ УНИВЕРСИТЕТ
9






 drafting
drafting








