Similar presentations:
Случайные события. Что такое случайное событие?
1. Случайные события
Что такое случайное событие?Случайное событие - это событие, которое может произойти или не
произойти, причем это можно выяснить только в результате
опыта.
Основная характеристика случайного события - это его вероятность частота появления события в большой серии опытов. Вероятность
события - это знания, которые существуют до проведения опыта.
Если в большой серии из N опытов событие X случилось nX раз,
можно говорить о том, что вероятность появлении события P(X)
примерно равна
Это приближенное равенство превращается в точное при
стремлении числа опытов N .
2. Случайные события
Случайные величиныРезультаты эксперимента можно выразить в виде числа, количественно.
Рассмотрим пример покупки в магазине резисторов номинального
сопротивления, например, 100 Ом. При изготовлении всегда есть
допуски, то есть, разрешенные отклонения от номинала. Например, при
допуске ± 3% сопротивление взятого наугад резистора может быть
любым числом в интервале от 97 до 103 Ом. Случайная величина - это
величина из определенного интервала. В общем случае интервал может
быть и бесконечным, например, от 0 до бесконечности.
3. Случайные события
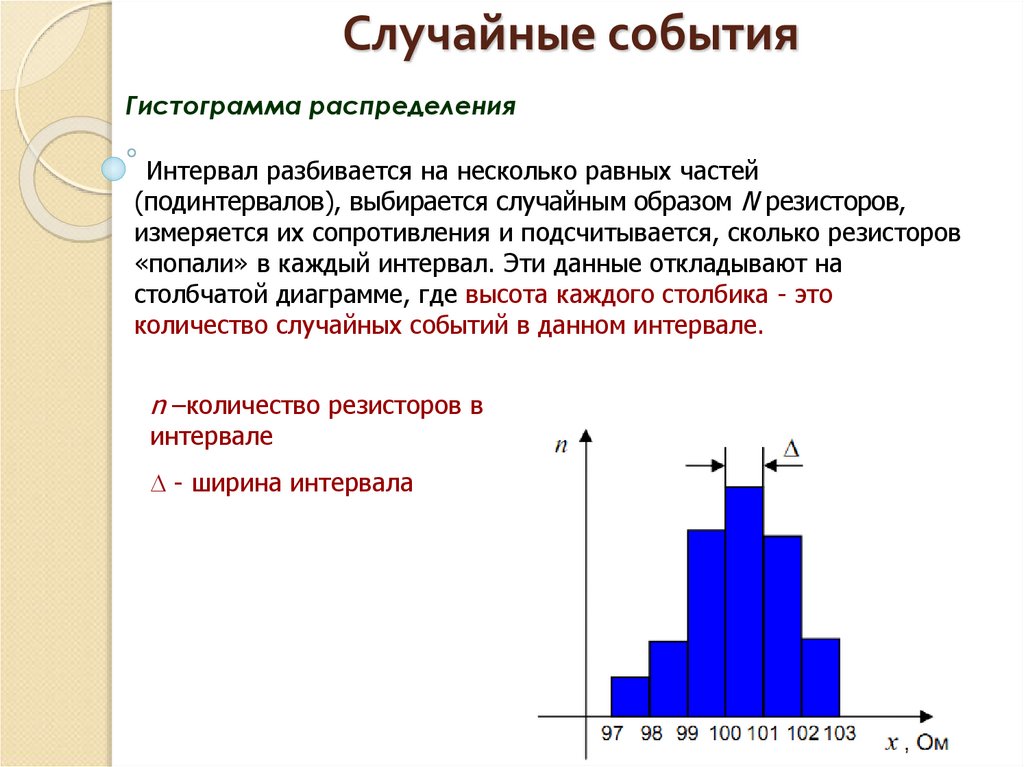
Гистограмма распределенияИнтервал разбивается на несколько равных частей
(подинтервалов), выбирается случайным образом N резисторов,
измеряется их сопротивления и подсчитывается, сколько резисторов
«попали» в каждый интервал. Эти данные откладывают на
столбчатой диаграмме, где высота каждого столбика - это
количество случайных событий в данном интервале.
n –количество резисторов в
интервале
- ширина интервала
4. Случайные события
Гистограмма распределенияНа гистограмме можно показывать не только количество, но и долю
резисторов, попавших в данный интервал. Например, если 100
резисторов из 1000 имеют сопротивление от 97 до 98 Ом, их доля
составляет 0,1 от общего числа (10%). Тогда высоту
соответствующего (первого) столбика гистограммы можно сделать
равной 0,1. При этом сумма высот всех столбиков будет равна 1 (или
100%).
При ширине интервала = 1 площадь всех столбиков также будет
равна 1. Такая гистограмма называется нормированной. Высота
столбика с номером i равна
hi =
где ni - число попыток (резисторов), «попавших» в i -ый интервал, а
N - их общее количество.
5. Случайные события
Плотность распределения вероятностейЕсли уменьшить ширину интервала в 2 раза и увеличить в 2 раза
N, то произведение N* остается постоянным. Фактически
каждый исходный интервал разбивается на 2 равных
подинтервала, n11 и n12 - количества резисторов в первом и
втором подинтервалах.
Поскольку общее количество резисторов удвоилось, в интервал
[97;98] (то есть в два новых подинтервала) попало примерно в 2
раза больше резисторов, то есть, n11 + n12 =2n1. Поэтому высота
обоих столбиков будет близка к тому, что было раньше. Было
только уточнено распределение резисторов внутри исходного
интервала [97;98].
6. Случайные события
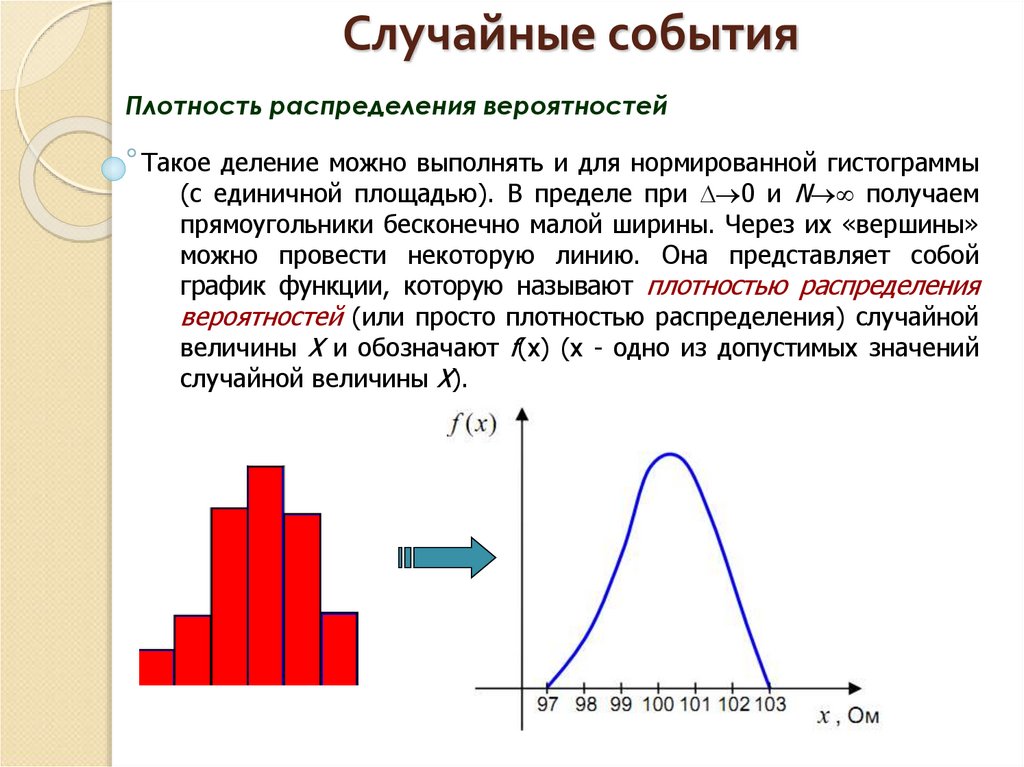
Плотность распределения вероятностейТакое деление можно выполнять и для нормированной гистограммы
(с единичной площадью). В пределе при 0 и N получаем
прямоугольники бесконечно малой ширины. Через их «вершины»
можно провести некоторую линию. Она представляет собой
график функции, которую называют плотностью распределения
вероятностей (или просто плотностью распределения) случайной
величины X и обозначают f(х) (х - одно из допустимых значений
случайной величины X).
7. Случайные события
Плотность распределения вероятностейТак как выполняется условие нормировки, площадь под этой линией
равна 1, она может быть вычислена как интеграл от функции f(х)
на всем множестве ее допустимых значений. Если заранее
известно, что величина х находится в некотором интервале [a; b],
получаем
В общем случае, если случайная величина может принимать любые
вещественные значения, справедлива формула
Интеграл от f(x) на некотором интервале [х1, х2] определяет
вероятность того, что случайная величина x при очередном
испытании окажется в этом интервале, то есть выполнится
неравенство x1 < x < x2.
Вероятность точного равенства x = x1 для некоторого заданного x1
вычисляется по формуле
Поскольку верхний и нижний пределы интегрирования совпадают,
для обычных функций такой интеграл равен нулю.
8. Случайные события
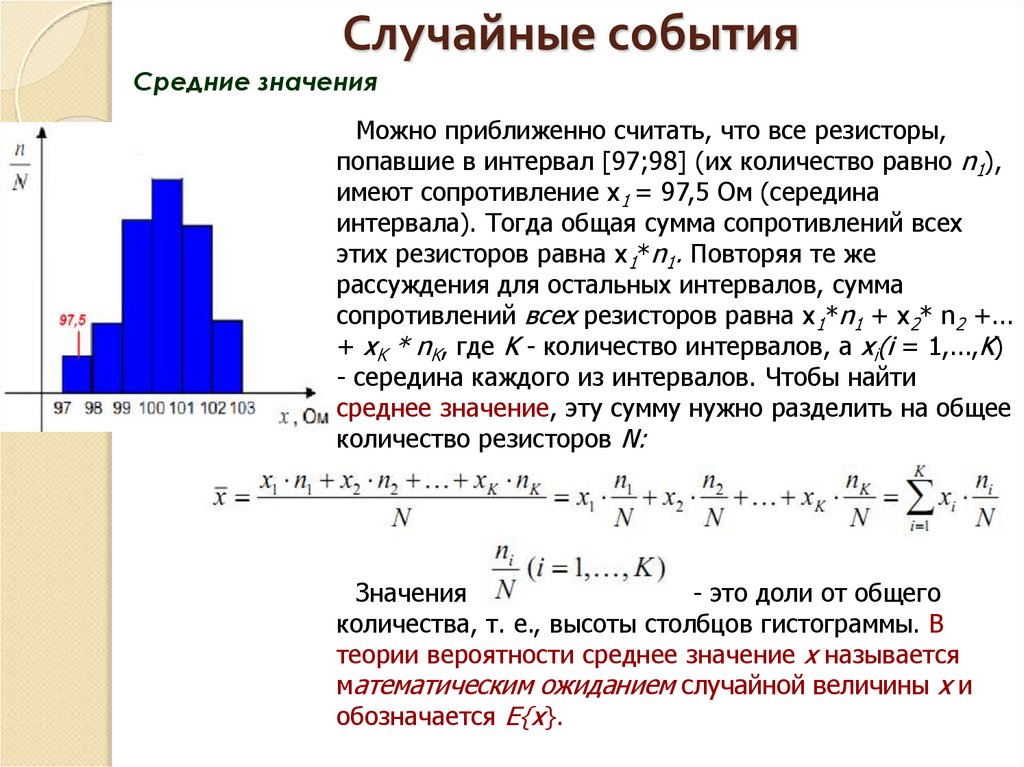
Средние значенияМожно приближенно считать, что все резисторы,
попавшие в интервал [97;98] (их количество равно n1),
имеют сопротивление х1 = 97,5 Ом (середина
интервала). Тогда общая сумма сопротивлений всех
этих резисторов равна х1*n1. Повторяя те же
рассуждения для остальных интервалов, сумма
сопротивлений всех резисторов равна х1*n1 + х2* n2 +...
+ xK * nK, где K - количество интервалов, а хi(i = 1,...,K)
- середина каждого из интервалов. Чтобы найти
среднее значение, эту сумму нужно разделить на общее
количество резисторов N:
Значения
- это доли от общего
количества, т. е., высоты столбцов гистограммы. В
теории вероятности среднее значение х называется
математическим ожиданием случайной величины х и
обозначается Е{х}.
9. Случайные события
Средние значенияНа языке теории вероятности разброс
относительно средней точки
называется дисперсией - эта величина
равна среднему квадрату отклонения
от среднего значения х . Дисперсия
вычисляется по формуле:
Если раскрыть скобки в подинтегральном выражении, видно, что
дисперсия равна разности среднего квадрата и квадрата
математического ожидания:
Если математическое ожидание равно нулю, дисперсия и средний
квадрат совпадают.
На практике чаще применяют среднеквадратическое отклонение
(СКВО)- квадратный корень из дисперсии:
В теории регулирования эту величину называют стандартное
отклонение.
10. Случайные события
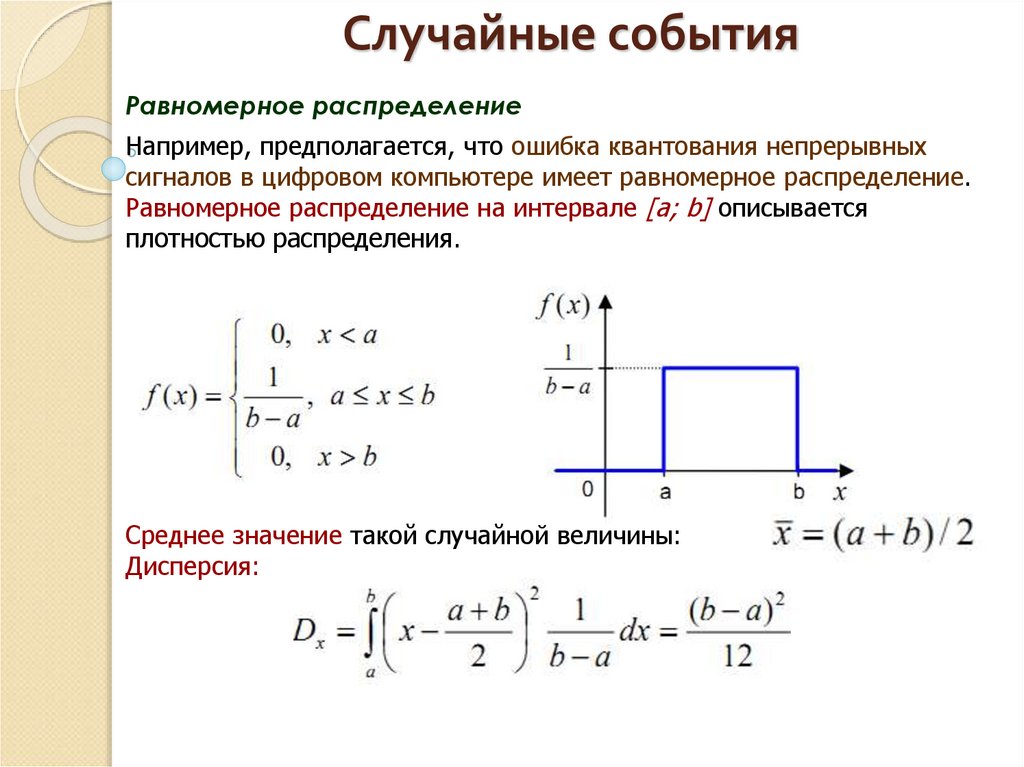
Равномерное распределениеНапример, предполагается, что ошибка квантования непрерывных
сигналов в цифровом компьютере имеет равномерное распределение.
Равномерное распределение на интервале [a; b] описывается
плотностью распределения.
Среднее значение такой случайной величины:
Дисперсия:
11. Случайные события
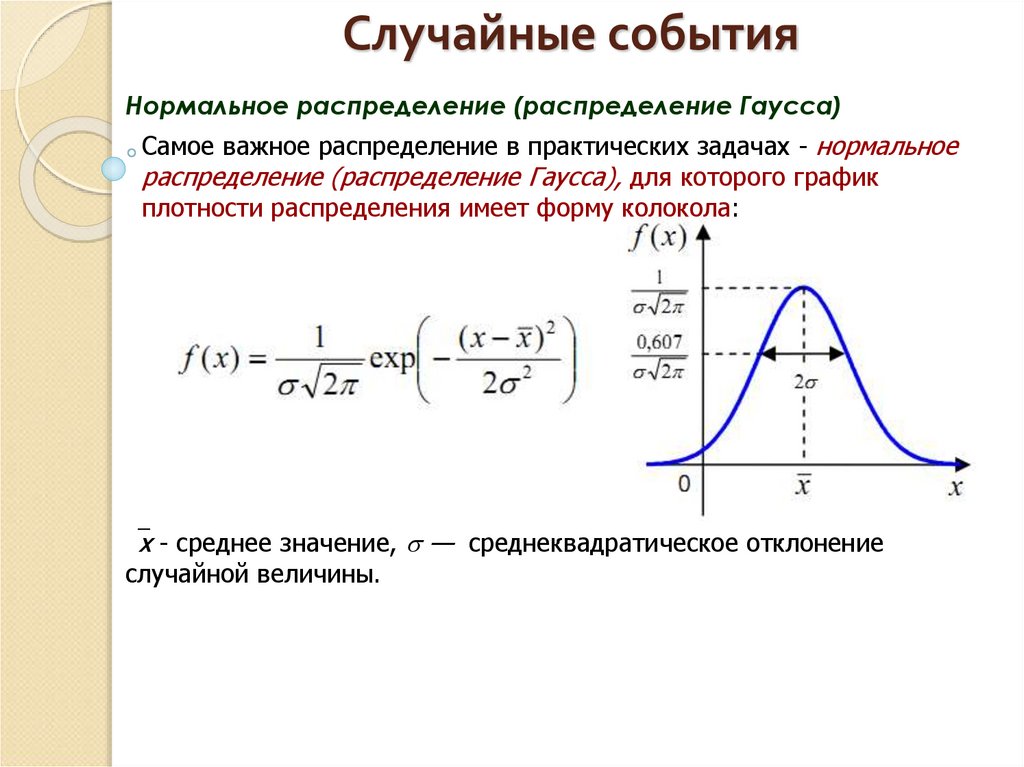
Нормальное распределение (распределение Гаусса)Самое важное распределение в практических задачах - нормальное
распределение (распределение Гаусса), для которого график
плотности распределения имеет форму колокола:
х - среднее значение, — среднеквадратическое отклонение
случайной величины.
12. Случайные события
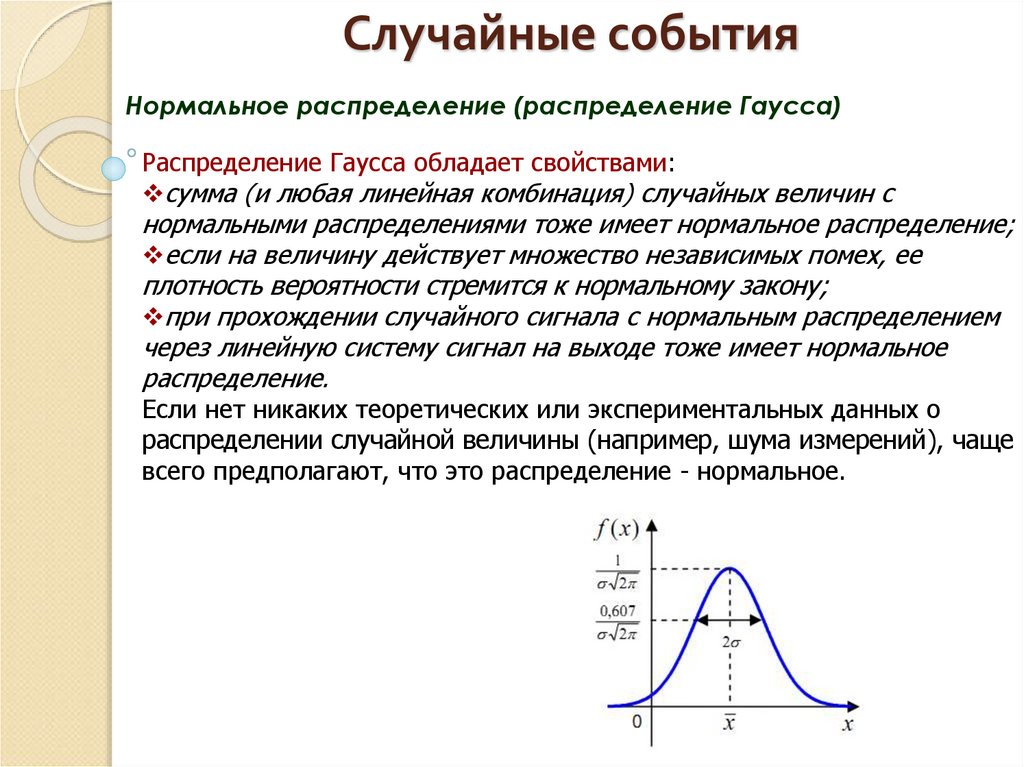
Нормальное распределение (распределение Гаусса)Распределение Гаусса обладает свойствами:
сумма (и любая линейная комбинация) случайных величин с
нормальными распределениями тоже имеет нормальное распределение;
если на величину действует множество независимых помех, ее
плотность вероятности стремится к нормальному закону;
при прохождении случайного сигнала с нормальным распределением
через линейную систему сигнал на выходе тоже имеет нормальное
распределение.
Если нет никаких теоретических или экспериментальных данных о
распределении случайной величины (например, шума измерений), чаще
всего предполагают, что это распределение - нормальное.
13. Случайные события
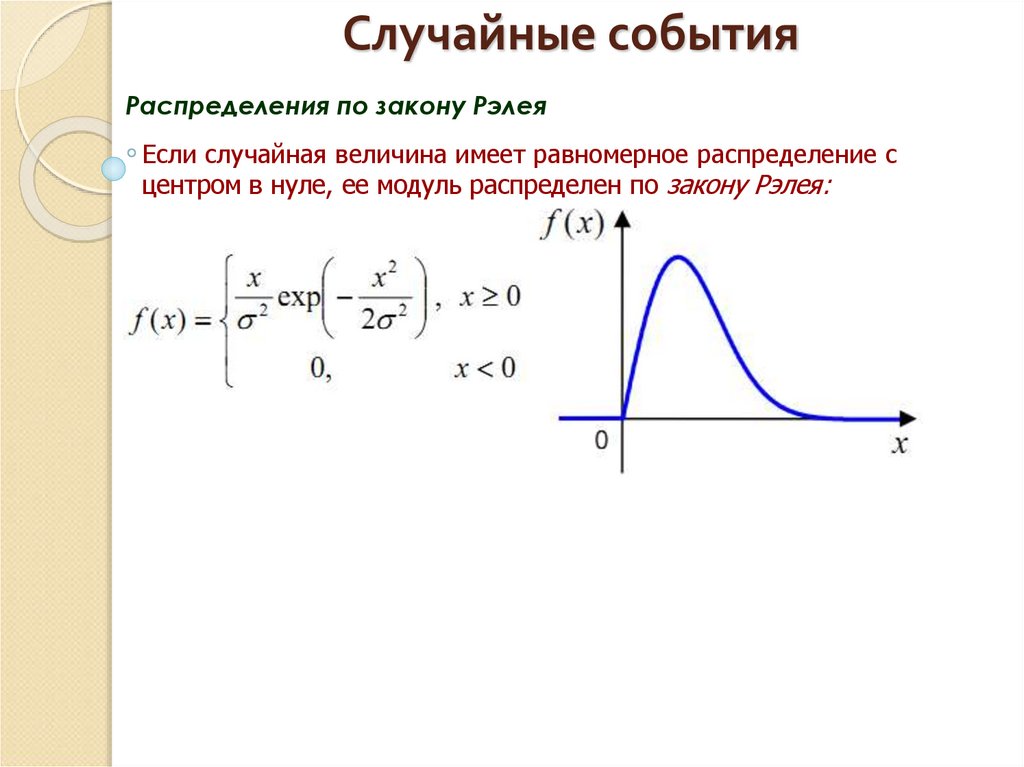
Распределения по закону РэлеяЕсли случайная величина имеет равномерное распределение с
центром в нуле, ее модуль распределен по закону Рэлея:






 mathematics
mathematics








