Тема 1.4 Ф-я корня, её св-ва, преобразования иррац-х выражений

1.

„Если ученик не прилагает
усилий к обучению, не имеет
терпения для практики, то
даже Учитель беспомощен.“
Цитата, основанная на священных писаниях

2.

Тест на повторение
Задание: вычислить.
[( 5) ( 7) ( 2) 10] [8 ( 12) ( 6)]
Ответ: 6.

3.

Тема 1.4
Функция корня, её свойства

4.

у
3
2
1
у х
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 х

5.

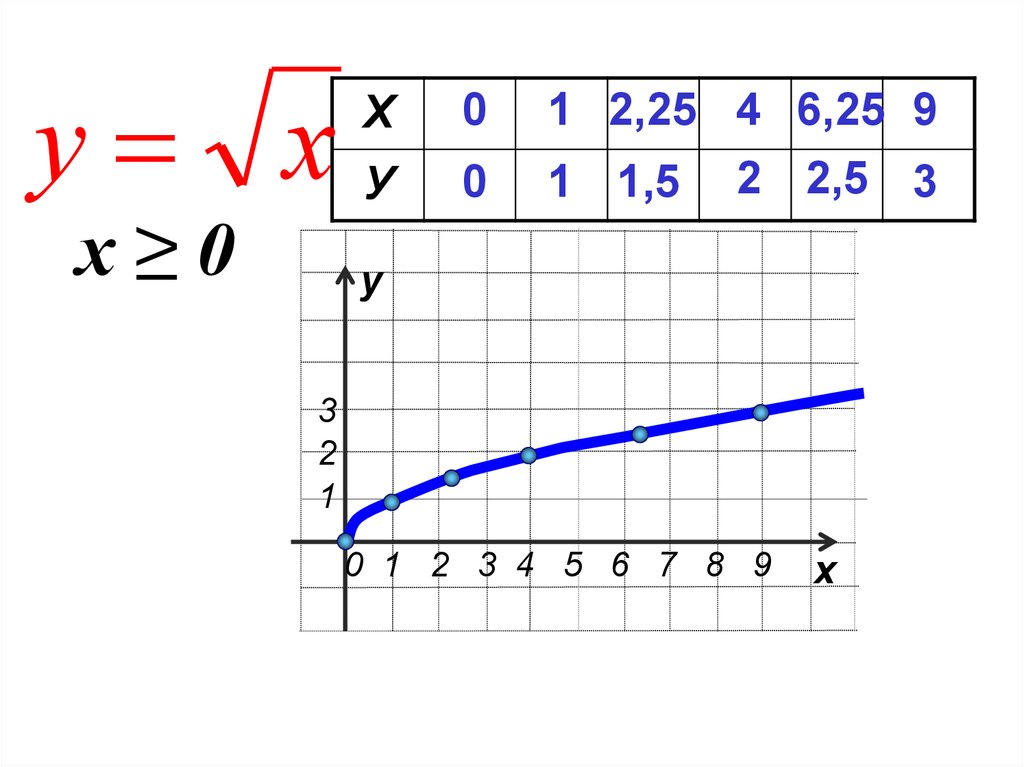
у х
х≥0
Х
0
У
0
1 2,25 4 6,25 9
1 1,5 2 2,5 3
у
3
2
1
0 1 2 3 4 5 6 7 8 9
х

6.

Свойства функции у=√х:
1.Область
1. D ( у ) 0 ;
определения
у
2.
2.Область
значений
3. у=0, если х= 0 4
у>0, если
3
E ( у ) 0;
х 0;
1
х
4. Функция
-1 0 1 2 3 4 5 6 7 8 9 10 11
возрастает
при х 0 ;
ограничена снизу, но не
5. Функция
Ограниченность
ограничена сверху.
6. унаим.= 0
Непрерывна.
7. Непрерывность
7.
унаиб.= НЕТ

7.

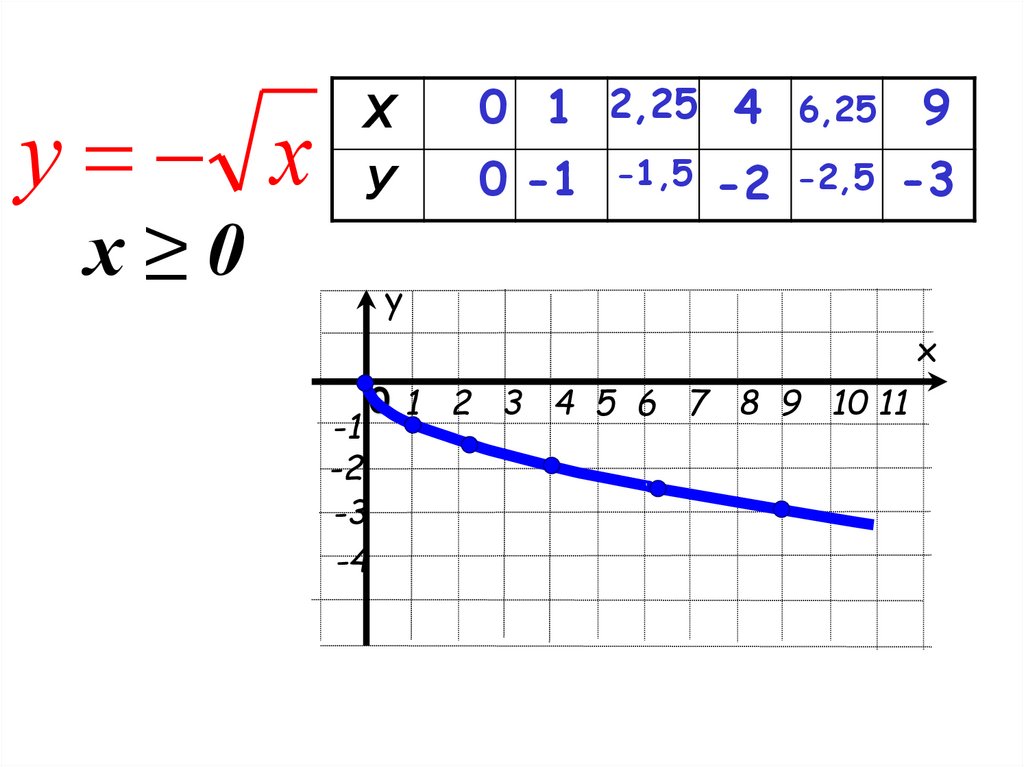
у х У
Х
х≥0
0 1 2,25 4
0 -1
6,25
9
-1,5 -2 -2,5
-3
у
х
0 1 2 3 4 5 6 7 8 9 10 11
-1
-2
-3
-4

8.

Свойст ва функции
ь;
1 D1.Област
(
у
)
0
у
. определения
2 E 2.Област
( у ) ь ; 0
значений
. у=0,
3.
если х= 0
0 1 2 3 4 5
-1
у<0, если
-2
х 0 ;
-3
4. Функция
-4
убывает
при
х 0;
х
6 7
8 9 10 11
5
.
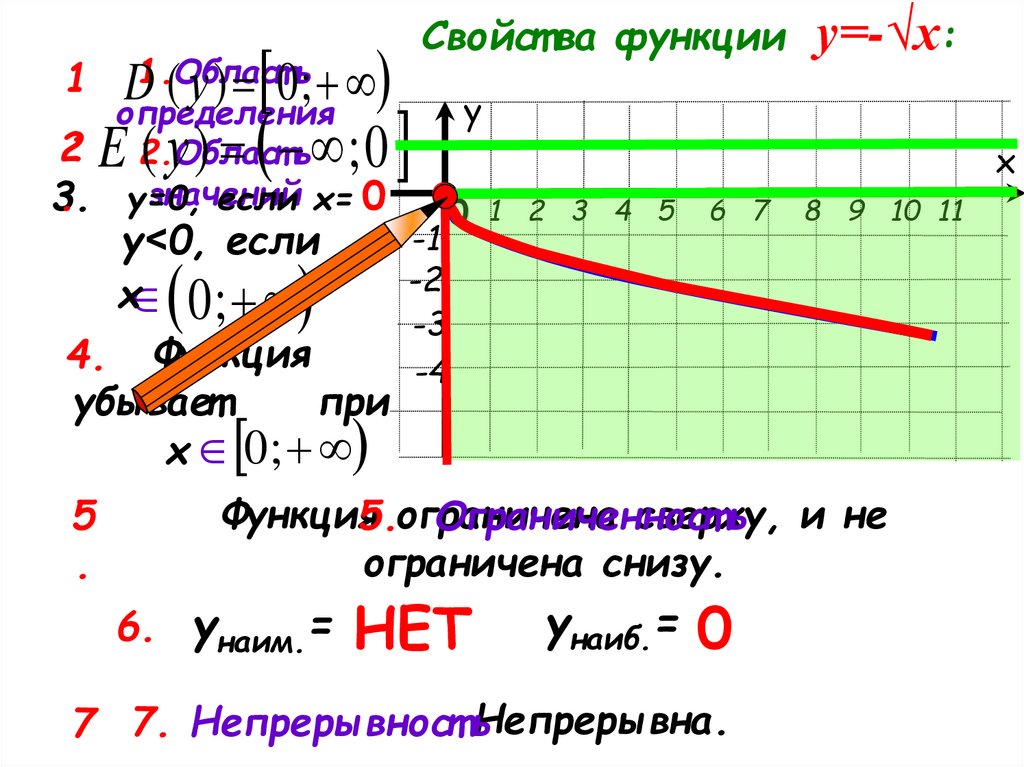
у=-√х:
Функция
сверху,
5.ограничена
Ограниченност
ь и не
ограничена снизу.
6. унаим.= НЕТ
унаиб.= 0
7 7. Непрерывност ьНепрерывна.

9.

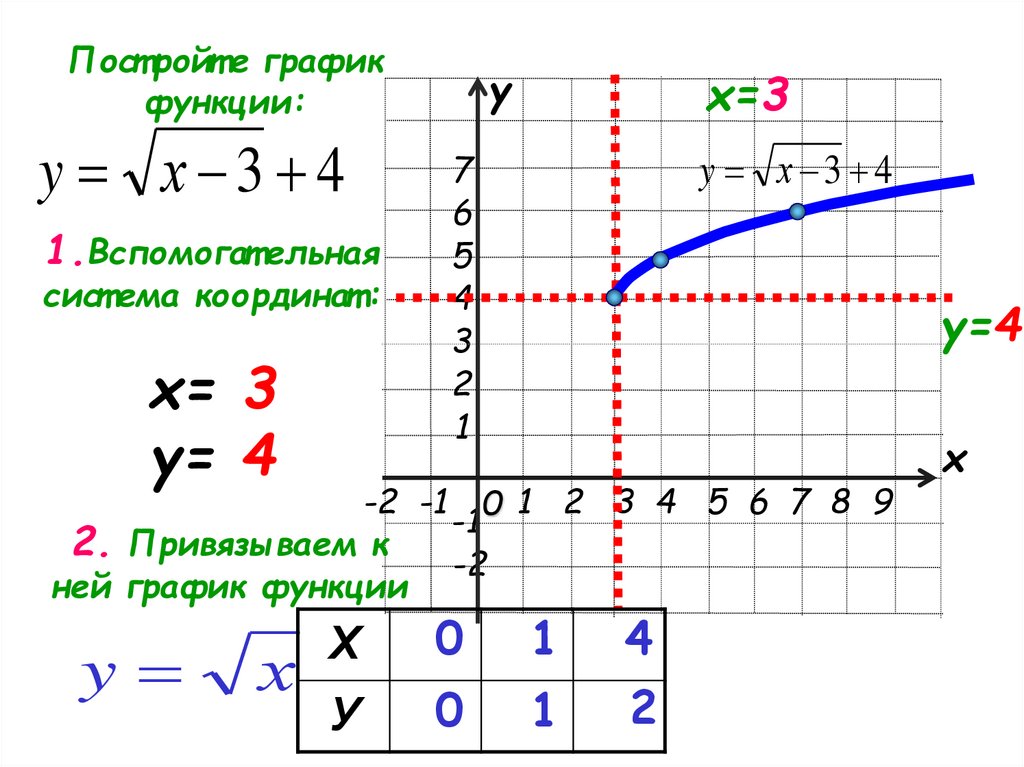
Пост ройт е график
функции:
y х 3 4
1.Вспомогат ельная
сист ема координат :
х= 3
у= 4
х=3
у
y х 3 4
7
6
5
4
3
2
1
у=4
-2 -1 0 1 2 3 4 5 6 7 8 9
-1
2. Привязываем к
-2
ней график функции
y
х
Х
0
1
У
0
1
4
2
х

10.

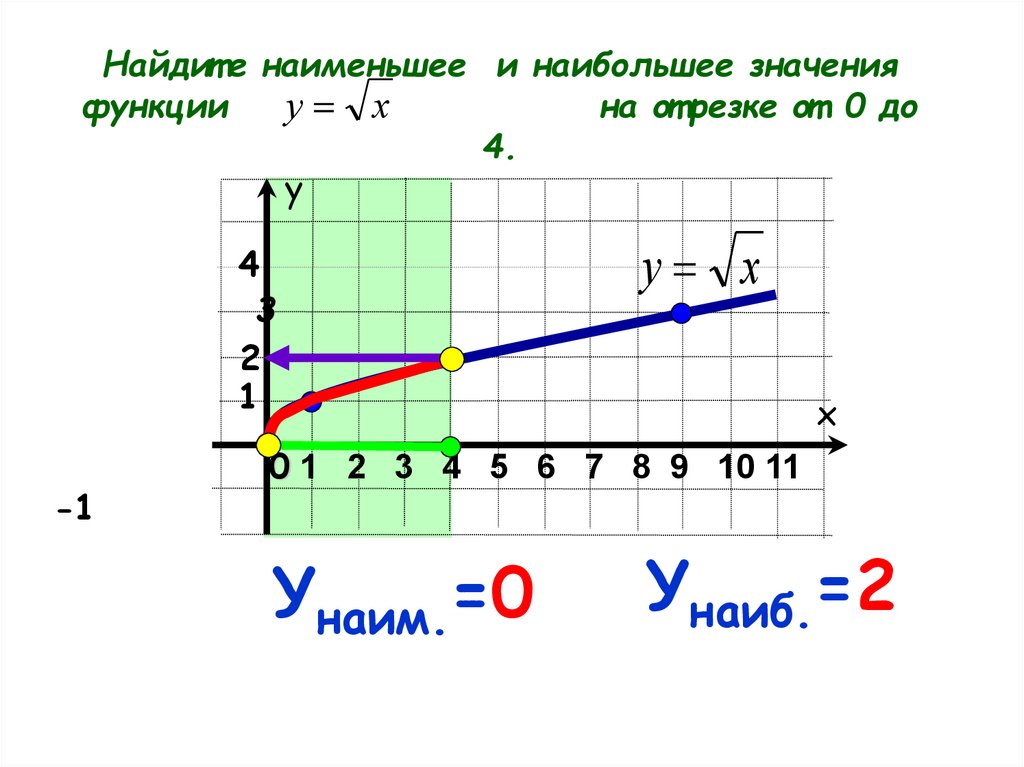
Найдит е наименьшее и наибольшее значения
функции
на от резке от 0 до
у х
4.
у
4
3
2
1
-1
у х
х
0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=0
Унаиб.=2

11.

Найдит е наименьшее и наибольшее значения
функции у х 2
на от резке от 3 до
11.
у
х=2
4
3
у х 2
1
-1
х
0 1 2 3 4 5 6 7 8 9 10 11
Унаим.=1
Унаиб.=3

12.

Решит ь графически уравнение:
√х=х-6
1
4
3
2
Пост роим в одной сист еме 1
координат графики функций:
у=√х
Х
У
0 1 4 9
0 1 2 3
у=х-6
Х 0 6
У -6 0
2
3
-1
-2
-3
-4
-5
-6
у
у х
х
0 1 2 3 4 5 6 7 8
9
у=х-6
Найдём абсциссы т очек
пересечения графиков
х=9
ОТВЕТ:

13.

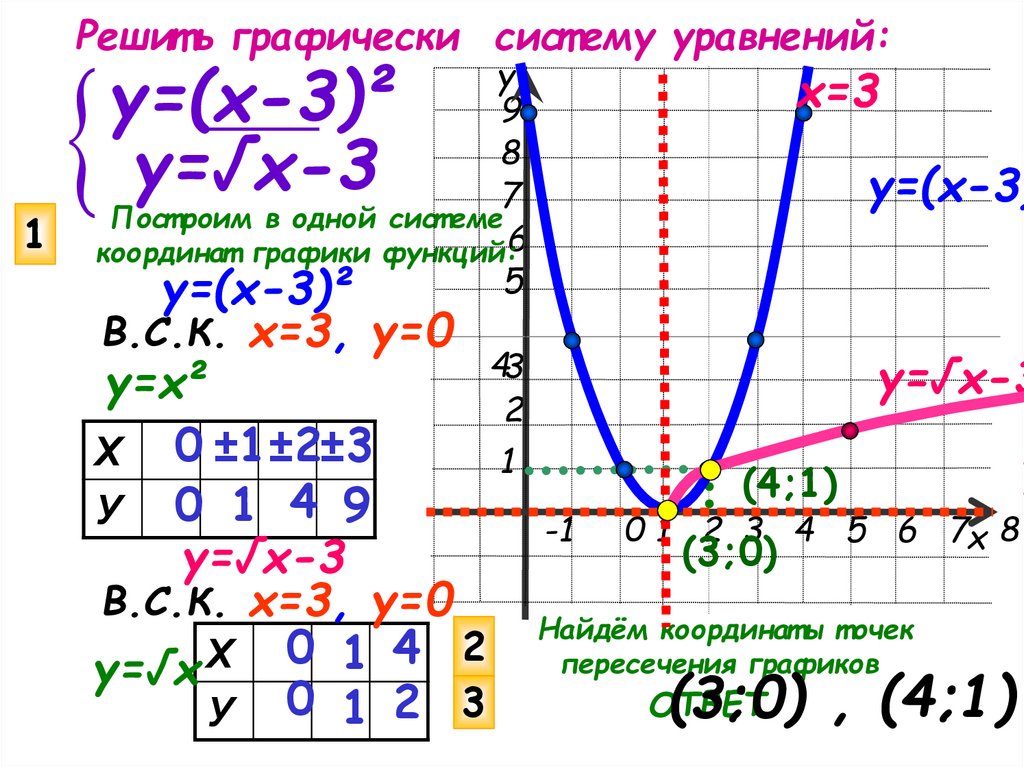
Решит ь графически сист ему уравнений:
1
у=(х-3)²
у=√х-3
у
9
8
7
Пост роим в одной сист еме
координат графики функций:6
5
у=(х-3)²
В.С.К. х=3, у=0
у=х²
Х 0 ±1 ±2±3
У 0 1 4 9
у=√х-3
В.С.К. х=3, у=0
2
0
4
Х
1
у=√х
У 0 1 2 3
х=3
у=(х-3)
43
2
1
у=√х-3
-1
(4;1)
0 1 2 3 4 5 6 7х 8
(3;0)
Найдём координат ы т очек
пересечения графиков
(3;0) , (4;1)
ОТВЕТ
у

14.

Корень n-й степени
Корень степени n числа b называется такое число a (если оно
существует), n-я степень которого равна b.
2 n 1
x
2n
x
1 корень, знак как у аргумента
2 корня с разными знаками
x ;
x [0; )
Арифметический корень степени n из числа b называется
неотрицательный корень степени n из неотрицательного b.

15.

График функции корня
2 n 1
x
2n
x

16.

Свойства
2n
(-∞;+∞)
D(f)
[0;+∞)
(-∞;+∞)
E(f)
[0;+∞)
Чётность /
нечётность
-/-
2 n 1
x
Нечётная, симметрия
относительно начала
координат
x
Возрастает (-∞;+∞)
Монотонность
Возрастает [0;+∞)
Не ограничена
Ограниченность
Снизу
-
у наибольшее
-
-
у наименьшее
0
Непрерывна
Непрерывность
Непрерывна
Выпукла вниз (-∞;0];
выпукла вверх [0:+∞)
Выпуклость /
вогнутость
Выпукла вверх [0;+∞)
y x 2 n 1
Обратная ф-я
y x 2n
Симметрия
относительно у=х
Симметрия
относительно у=х

17.

Тема 1.4
Свойства корней

18.

n
6.1. a a
n

19.

Тема 1.4
Преобразования
иррациональных выражений

20.

Домашняя работа
(обязательно к выполнению)
Найдите значения выражений
1
5
2
6
3
7
4
8
9

21.

Домашняя работа
(дополнительно, но желательно)
Найдите значения выражений
1
5
2
6
3
7
4

22.

Сократить дробь:
(обязательно к выполнению)
1
2

23.

Благодарю всех за работу!
Желаю хорошего дня!