Similar presentations:
Метод проецирования (лекция № 1 - 24)
1.
МясоедовСергей Александрович
Курс лекций
"НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ"
2.
Лекция 1Содержание:
Предмет начертательная геометрия
Метод проецирования
Свойства ГО при ортогональном проецировании
Понятие комплексного чертежа
Задание новой плоскости проекций
Задание точки и линии на чертеже
Принадлежность точки прямой
Прямые общего и частного положения
Способ прямоугольного треугольника
Взаимное расположение прямых
Конкурирующие точки
Мясоедов С.А.
2/28
3.
Чертёж – это своеобразный геометрический язык,понятный технически грамотному человеку.
Начертательная геометрия изучает построения
изображений, полученных проекционным методом.
Для осуществления проекционного метода
необходимо иметь:
трёхмерное пространство (мы в нём находимся)
поверхность, на которую будем осуществлять
проецирование (плоскость)
направление проецирования
объект проецирования – геометрический образ (ГО)
В данном курсе будем изучать прямоугольное
проецирование, которое называют ортогональным.
Мясоедов С.А.
3/28
4.
Если проецировать ГО ортогонально на две или болеевзаимно перпендикулярные плоскости, то получим
чертёж,
который
может
обладать
свойством
обратимости.
Основоположник этого метода крупный французский
геометр и инженер Гаспар Монж (1746-1818г.).
Метод ортогонального проецирования является
основным при составление технических чертежей.
Количество плоскостей, используемое при
проецировании зависит от сложности ГО и может
достигать шести (грани куба), но в начертательной
геометрии применяют обычно две или три плоскости
проекций, так как рассматривают простые объекты.
Мясоедов С.А.
4/28
5.
Основные виды1
3
2
Мясоедов С.А.
5/28
6.
Прямая и обратная задачаКомплексный чертёж
Наглядное изображение
П2
П2
А2
А2
А
0
х
П1
0
х
А1
А1
П2 П1
Мясоедов С.А.
П1
6 /28
7.
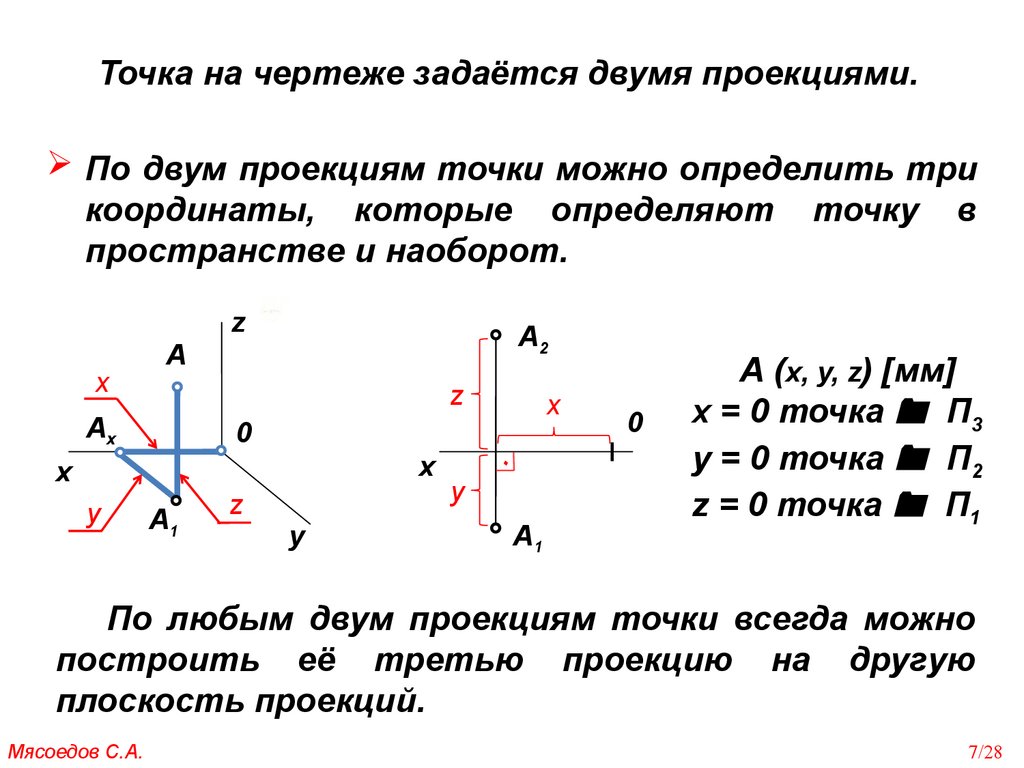
Точка на чертеже задаётся двумя проекциями.По двум проекциям точки можно определить три
координаты, которые определяют точку в
пространстве и наоборот.
A2
z
Aх
0
y
z
x
A1
x
y
x
.
x
A
z
y
A1
0
А (x, y, z) [мм]
x = 0 точка П3
y = 0 точка П2
z = 0 точка П1
По любым двум проекциям точки всегда можно
построить её третью проекцию на другую
плоскость проекций.
Мясоедов С.А.
7/28
8.
Построение третьейпроекции точки
z
z
П2
П2
А2
П3
А
А3
А2
П3
А3
x
0
П1
А1
0
x
y
y
А1
П1
y
Мясоедов С.А.
8/28
9.
В соответствии с условными обозначениямиизложенными в рабочей тетради (стр. 2) :
П1 - горизонтальная плоскость проекций
П2 - фронтальная плоскость проекций
П3 – профильная плоскость проекций
ох, оy, оz – оси координат
А1 - горизонтальная проекция точки А
А2 - фронтальная проекция точки А
А3 - профильная проекция точки А
А - точка в пространстве
[АА1], [АА2], [АА3] - проецирующие лучи
(А2А1), (А2А3) – линии проекционной связи
П1 П2 П3 П1 П2
Мясоедов С.А.
9/28
10.
Введение дополнительной плоскости проекций(замена плоскостей проекций)
П2
П2
А2
А
А3
х1 2
П1
А1
х1 2
.
.
А1
3
П1
П3
х1
.
3
Мясоедов С.А.
0
х1
П3 П1
3
А3
0
А2
П
10/28
11.
Введение дополнительной плоскости проекций(замена плоскостей проекций)
П2
А2
А2
.
А
А5
х1 2
П1
х2 5
П5
х1 2
А5
А1
П5 П 2
Мясоедов С.А.
2=
52
2=
5
х2 5
А1
11/28
12.
Линия – это след движущейся в пространстве точки.Линии могут быть прямыми и кривыми.
Кривые линии подразделяются на плоские и
пространственные.
Прямая – это кратчайшее расстояние между двумя
точками.
Прямая может занимать три различных положения
относительно плоскости проекций:
1. Прямая не параллельна ни одной из трёх
плоскостей проекций (прямая общего положения).
2. Прямая параллельная одной плоскости проекций
(прямая уровня).
3. Прямая
параллельная
одновременно
двум
плоскостям проекций (проецирующая прямая).
Мясоедов С.А.
12/28
13.
Прямая на комплексном чертеже задаётся двумяпроекциями
(кроме
профильной
прямой)
или
проекциями пары точек.
Проекциями:
Парой точек:
П2
П2
а2
А2
0
x
0
x
А1
а1
П1
В2
В1
П1
От одного задания прямой можно легко перейти к
другому.
Мясоедов С.А.
13/28
14.
Свойство принадлежности точки прямой:Точка принадлежит прямой, когда её одноимённые
проекции лежат на одноимённых проекциях прямой
и связаны между собой одной линией проекционной
связи перпендикулярной оси проекций.
А а
П2
a2
А2
(D2)
В1
С2
В а
E2
F2
0
x
а1
П1
Мясоедов С.А.
А1
В2
С1
С а
D а
D1
E1
(F1)
Е а
F а
14/28
15.
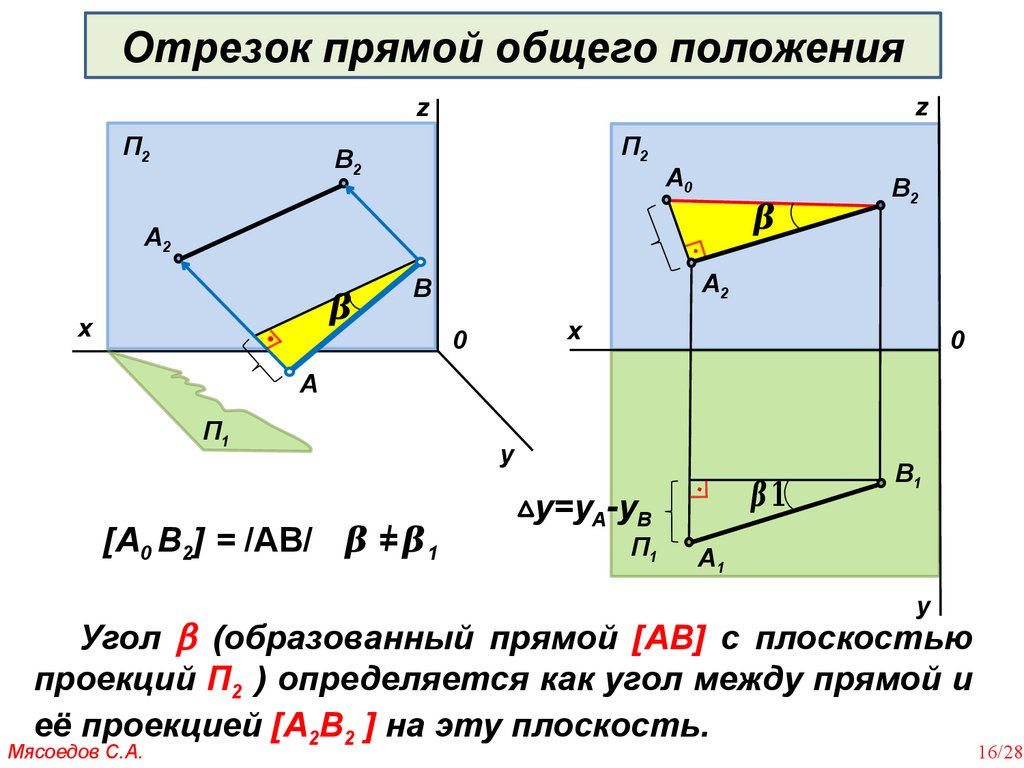
Отрезок прямой общего положенияz
П2
П2
В





























 drafting
drafting