Построение графиков функций с помощью геометрических преобразований

1.

«Построение графиков
функций с помощью
геометрических
преобразований»

2.

Повторение
Графиком
функции называется
множество точек координатной
плоскости, у которых значения х и у
связаны некоторой зависимостью и
каждому значению х соответствует
единственное значение y.

3.

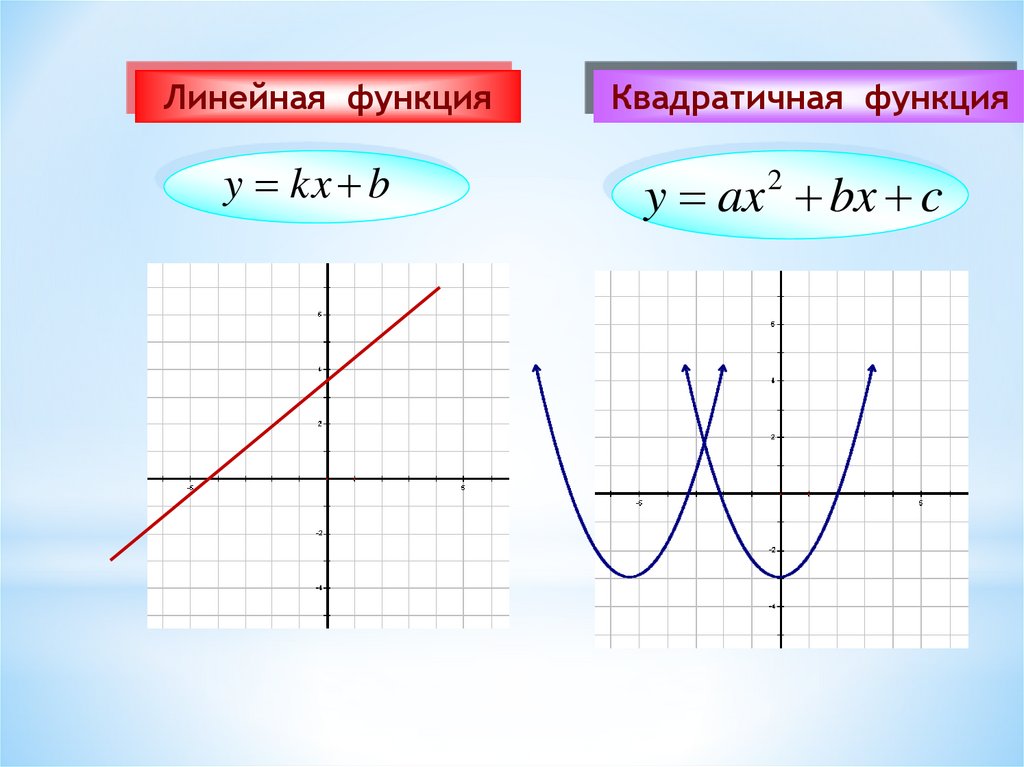
Линейная функция
Квадратичная функция
y kx b
y ax bx c
2

4.

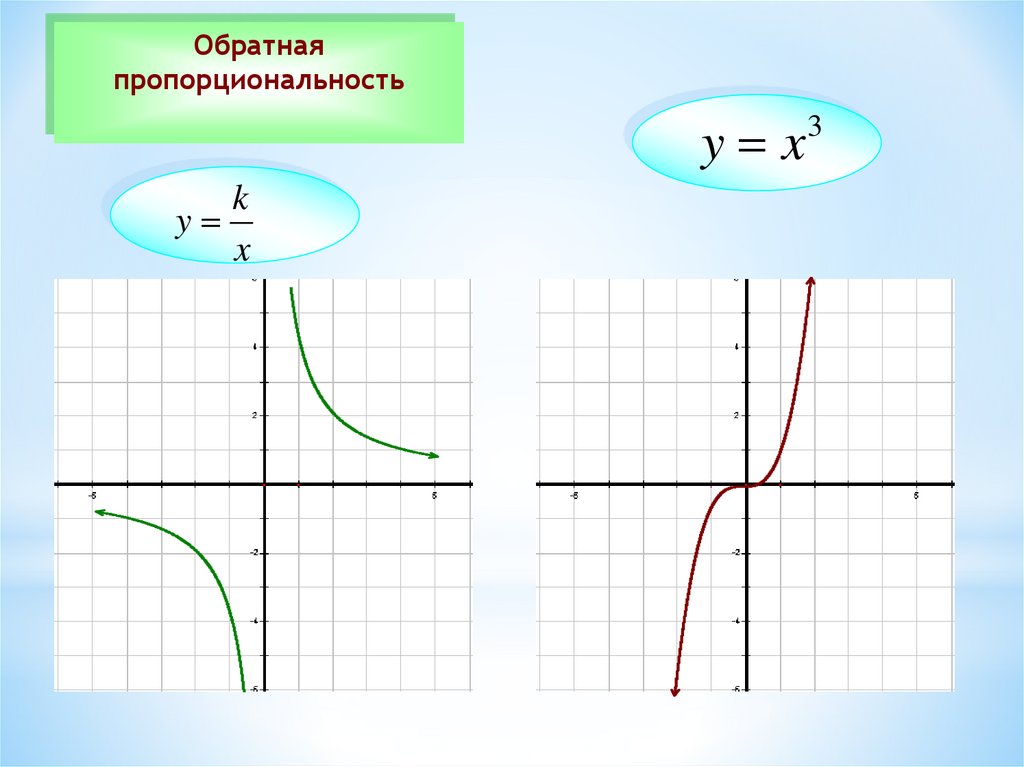
Обратная
пропорциональность
y x
k
y
x
3

5.

y
Функция
x
4
2
-5
5
-2
-4
-6
10

6.

Изучение нового материала:
Преобразование
графиков

7.

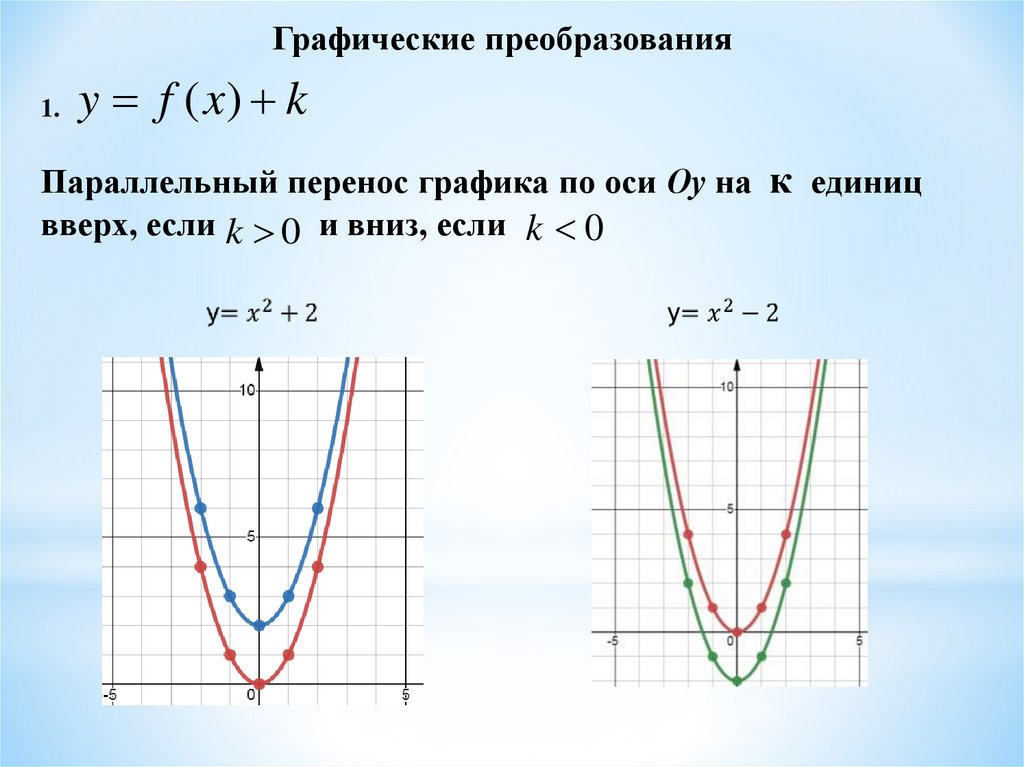
Графические преобразования
1.
y f ( x) k
Параллельный перенос графика по оси Оу на к единиц
вверх, если k 0 и вниз, если k 0

8.

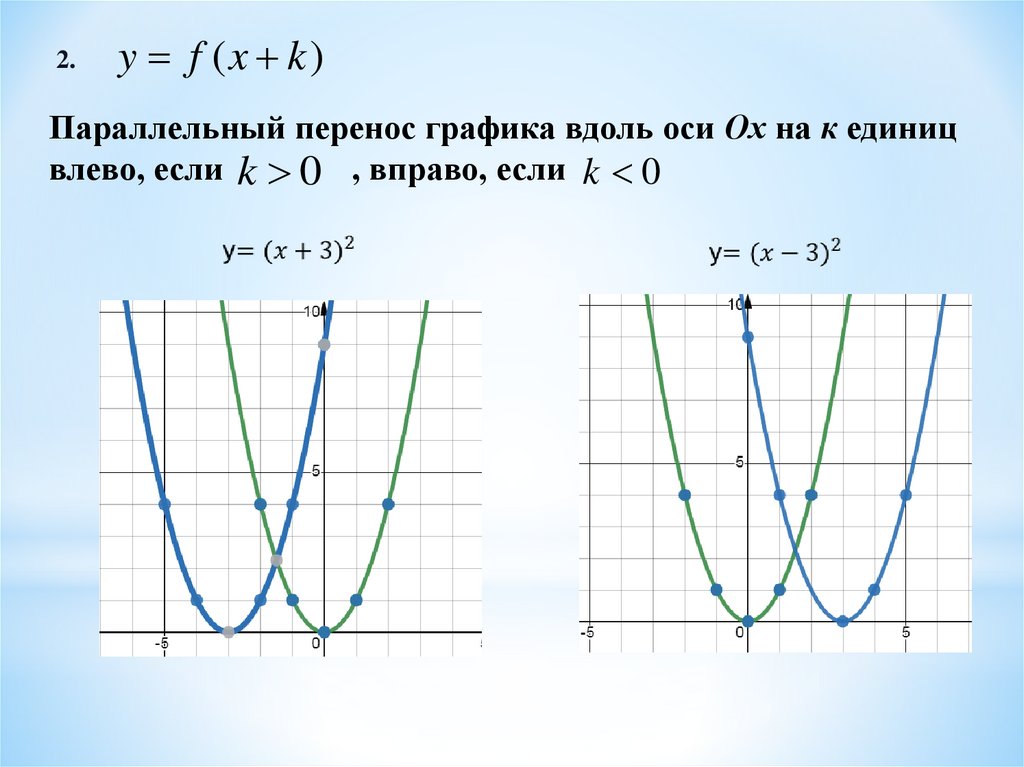
2.
y f (x k)
Параллельный перенос графика вдоль оси Ох на к единиц
влево, если k 0 , вправо, если k 0

9.

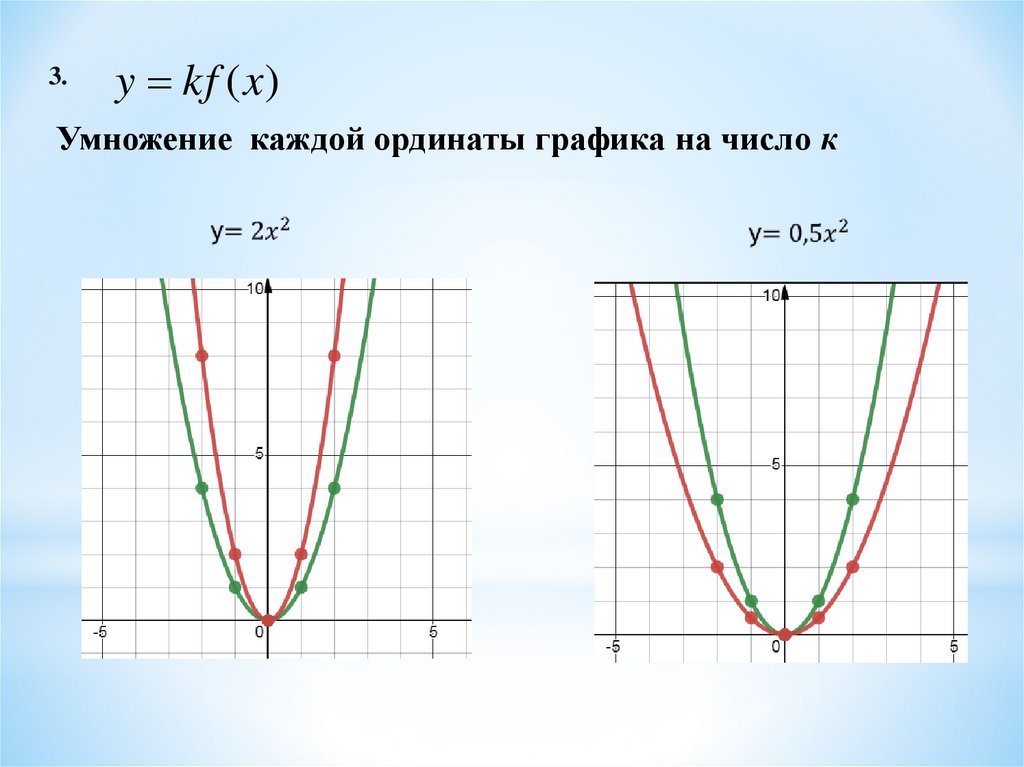
3.
y kf (x)
Умножение каждой ординаты графика на число к

10.

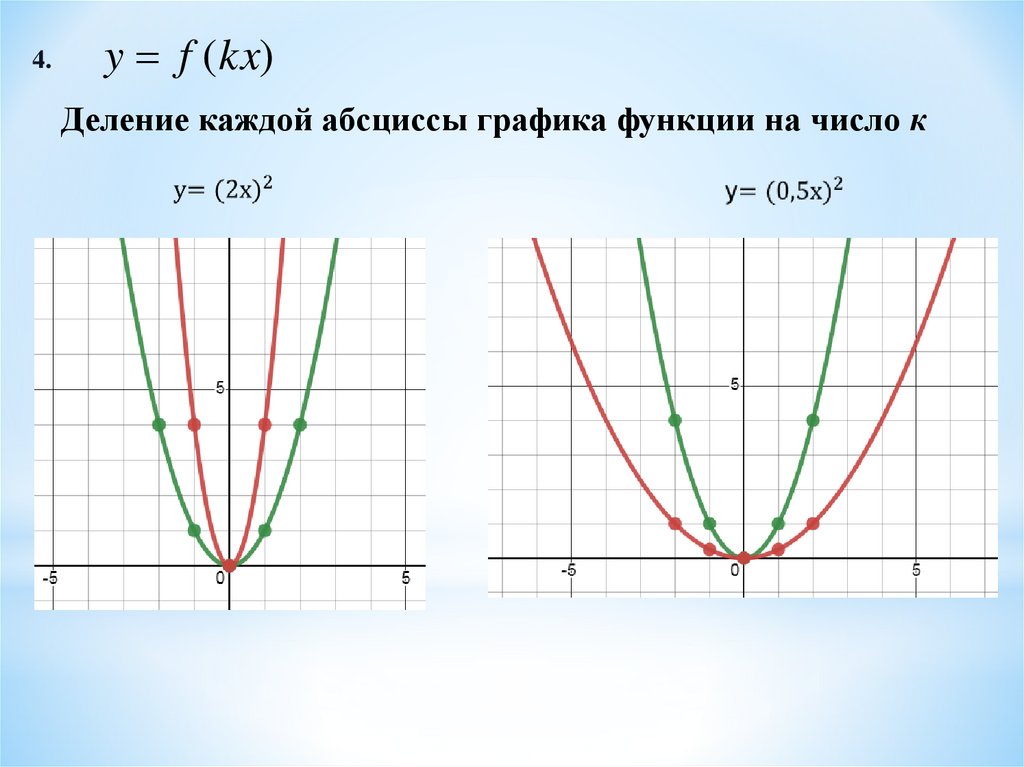
4.
y f (kx)
Деление каждой абсциссы графика функции на число к

11.

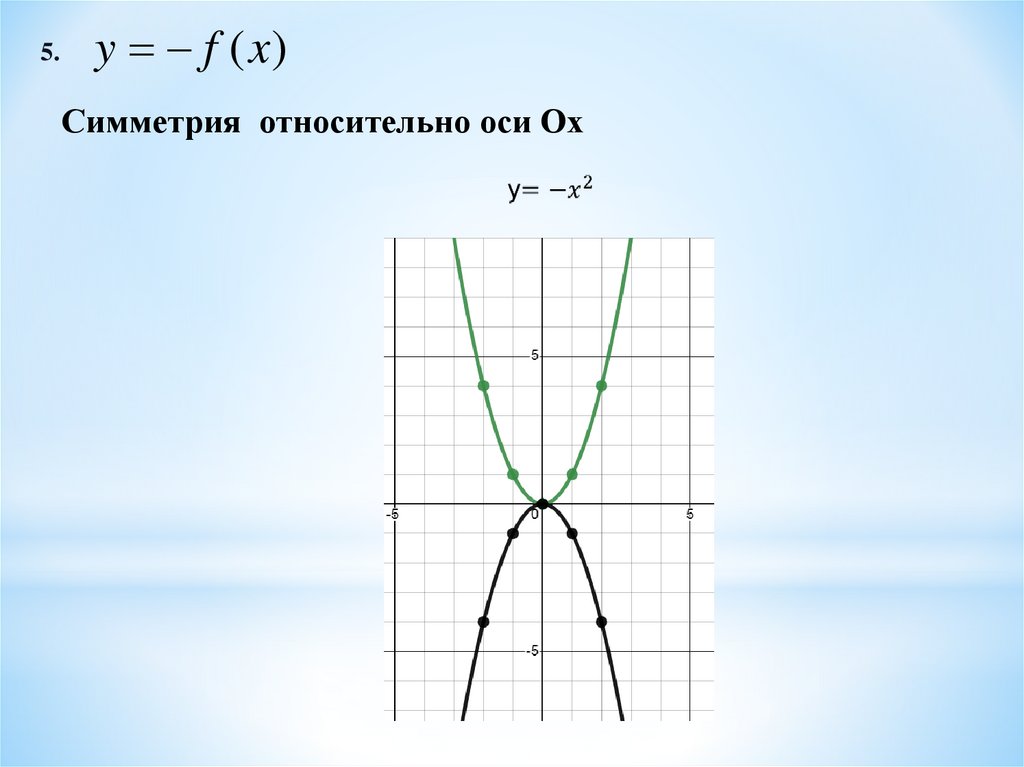
5.
y f (x)
Симметрия относительно оси Ох

12.

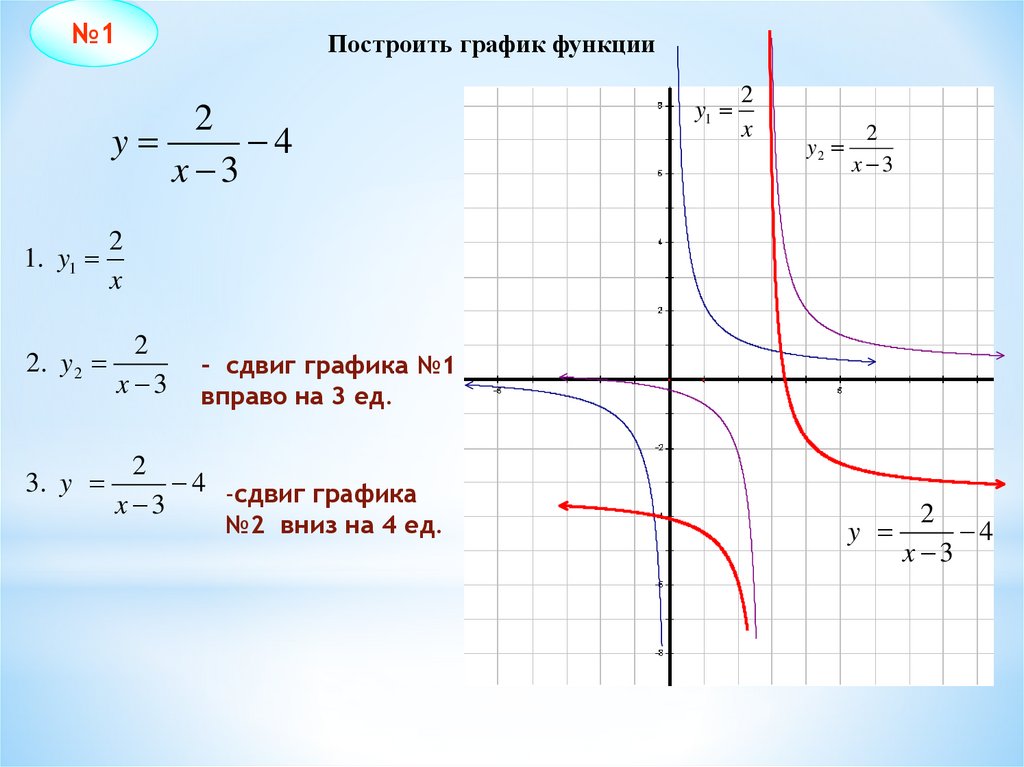
№1
Построить график функции
2
y
4
x 3
1. y1
2
x
2. y 2
2
x 3
3. y
2
4 -сдвиг графика
x 3
y1
2
x
y2
2
x 3
- сдвиг графика №1
вправо на 3 ед.
№2 вниз на 4 ед.
y
2
4
x 3

13.

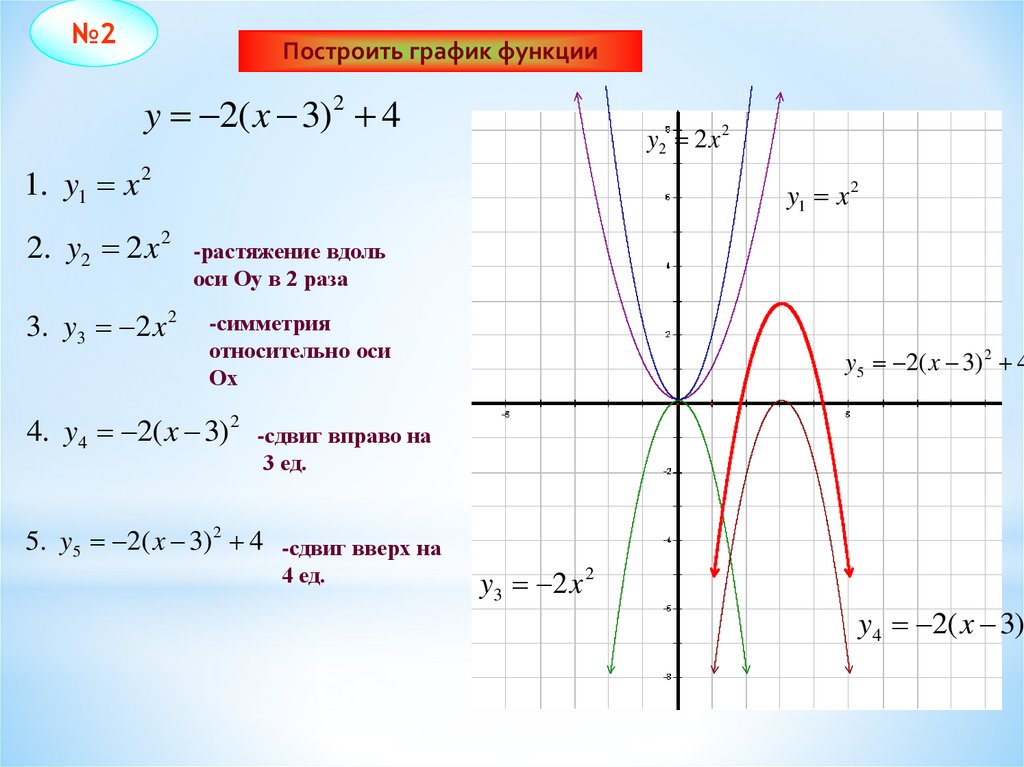
№2
Построить график функции
y 2( x 3) 2 4
y2 2x 2
1. y1 x 2
2. y2 2 x 2
3. y3 2 x 2
y1 x 2
-растяжение вдоль
оси Оу в 2 раза
-симметрия
относительно оси
Ох
y5 2( x 3) 2 4
4. y4 2( x 3) 2 -сдвиг вправо на
3 ед.
5. y5 2( x 3) 2 4 -сдвиг вверх на
4 ед.
y3 2x 2
y4 2( x 3)

14.

x 2 y 2 36
y 3 при 3 x 1 и 1 x 3
y
1 2
x 4 при 2 x 2
2
y 1 при 1 x 1
y 1 при 1 x 1
x 1 при 1 y 1
x 1 при 1 y 1
y x при 6 y 4 и 4 x 6
y x 12 при 6 y 4
y x 12 при 6 y 4
y x 12 при
6 x 8
y x 12 при
6 x 8
y x 2 10 при 2 x 2
y 6 при 3 x 3
y x при 6 y 4 и 4 x 6
Задание на дополнительную оценку:
построить данные графики
в прямоугольной системе координат.