Similar presentations:
Hyperbolic numbers
1.
Hyperbolic numbers2.
DefinitionA hyperbolic number is a number of the form:
Z = a + bj, a, b ∈ ℝ
2
Where = 1, j ≠±1
3.
These numbers are distributive :z, u, w: z(u + w) = zu + zw
4.
z: 1 → a+ bjz: j → b+ aj
z ↔ Z=
2
2
det(Z) = a − b
5.
Divisors of 0:a(1 ± j), a ∈ ℝ:
2
2
a(1 + j) ∙ b(1 − j) = ab(1 − j ) =
ab(1 − 1) = 0
6.
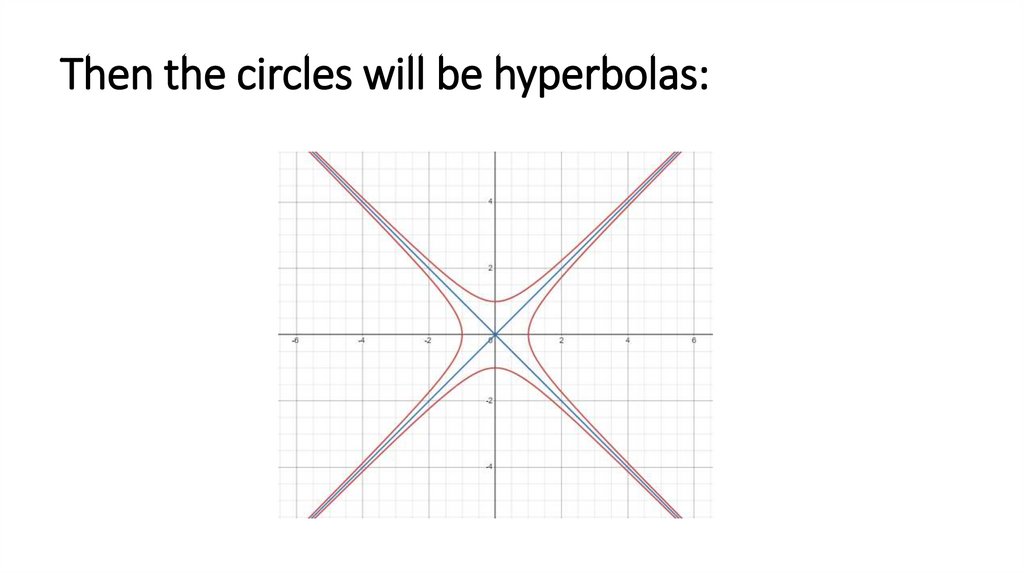
Then the circles will be hyperbolas:7.
Functionsw(z)= u(z) + v(z)j
=
=
8.
Lengtht2
l =
a2t − b2t dt =
t1
t2
t1
| |≤1
1 − x2t dt
9.
Define exp:= lim 1+
→∞
=... = ∙
( ℎ( ) + ∙ ℎ( ))
δ ∈ { ± 1, ± j}
z=
∙
10.
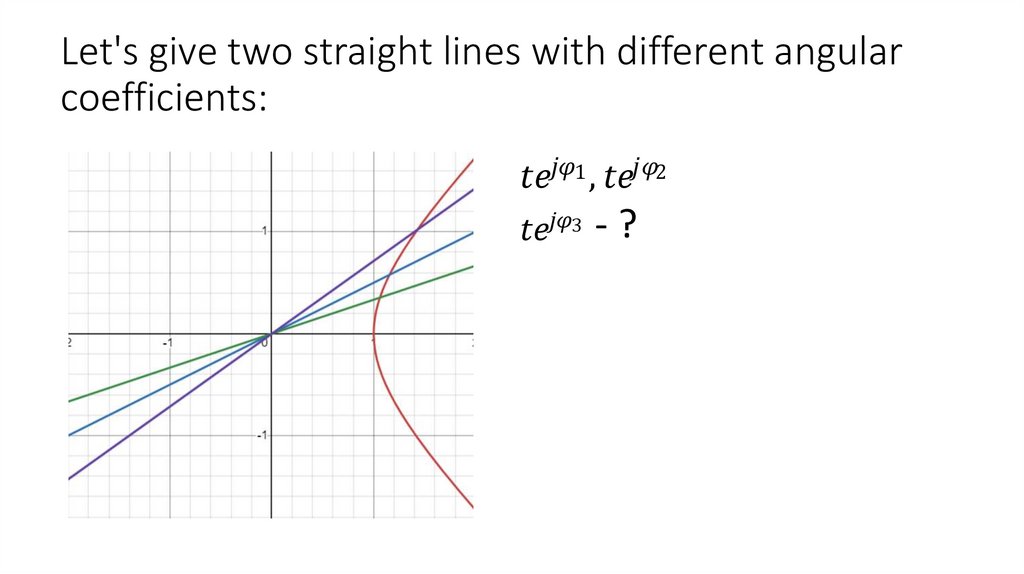
Let's give two straight lines with different angularcoefficients:
1
,
3
-?
2
11.
3 == ath( =
1 1+
1 + 2 = ath( 1) + ath( 2) = ln
2 1−
1+
1 1+
) = ln
2 1−
1+
∙
1 1−
1
2
1
1+ 1+
+
2
1
1+ 2
1 2
= ln
= ath(
)
+
2
1
2
1+
2
1 2
1 − 1+
2
1 2


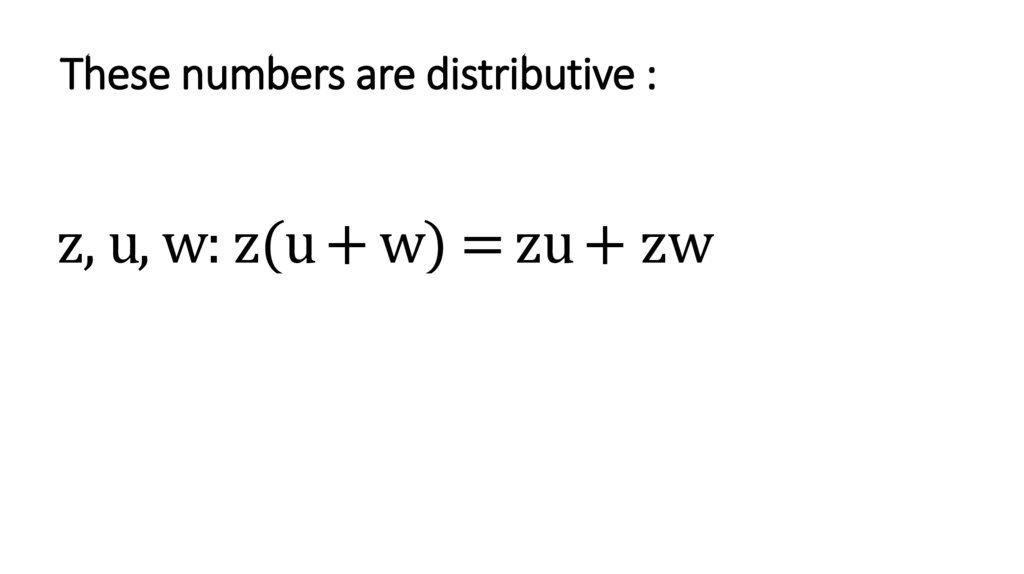
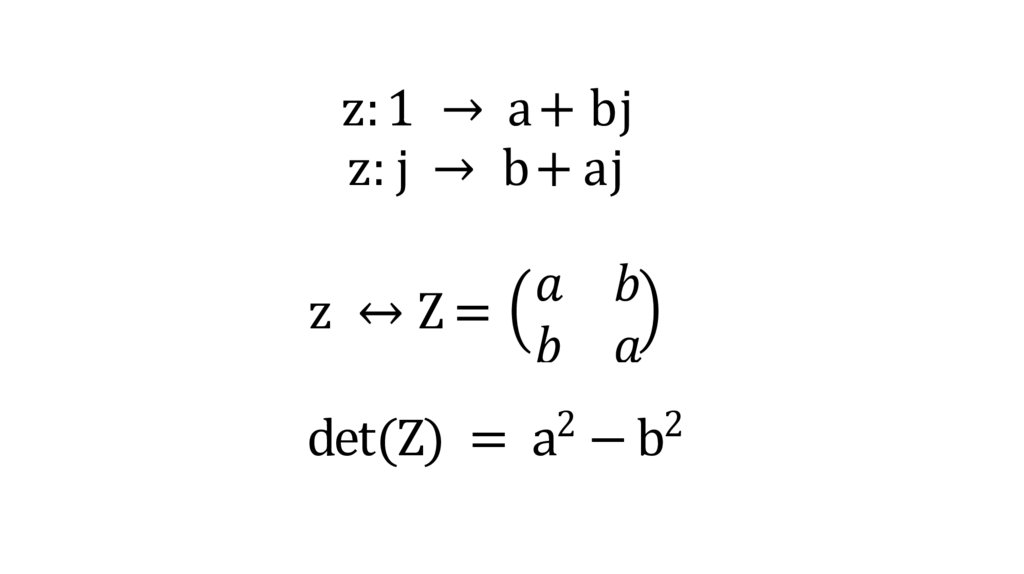
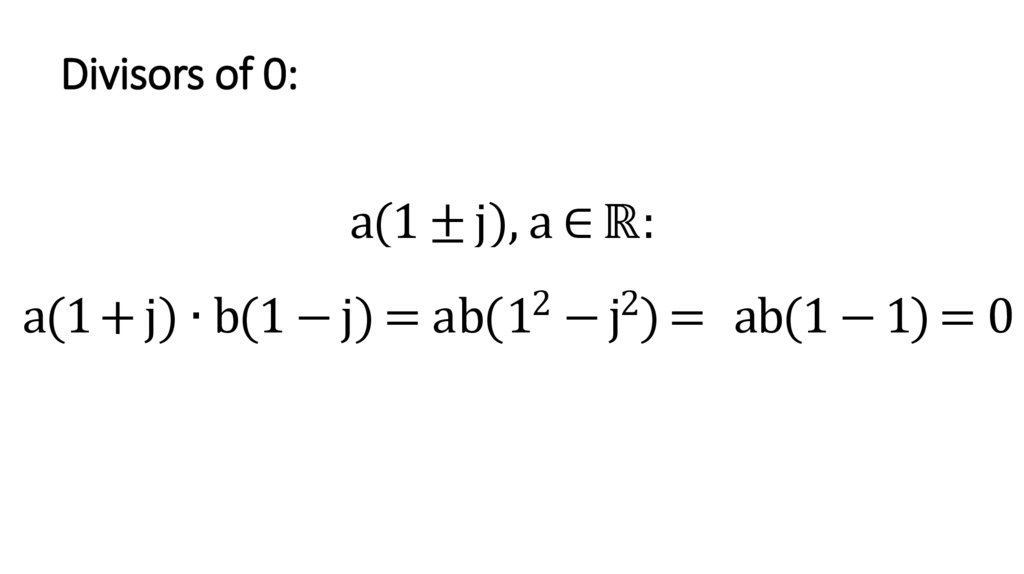
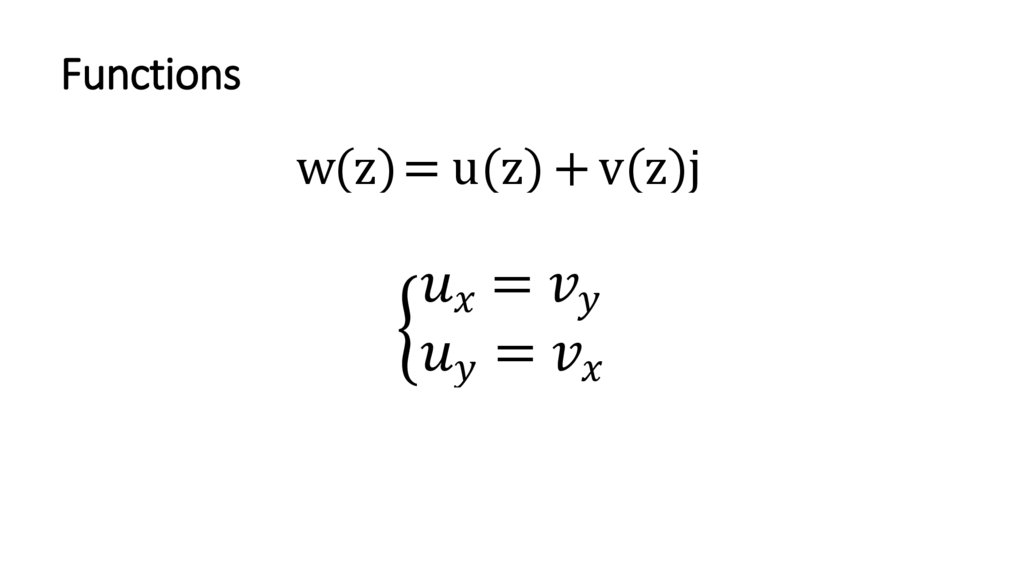
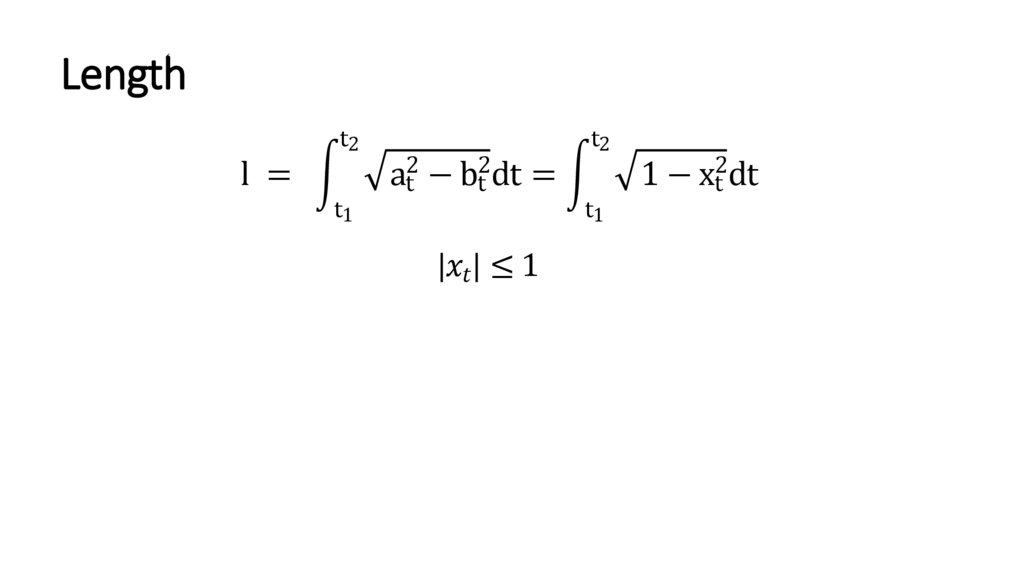
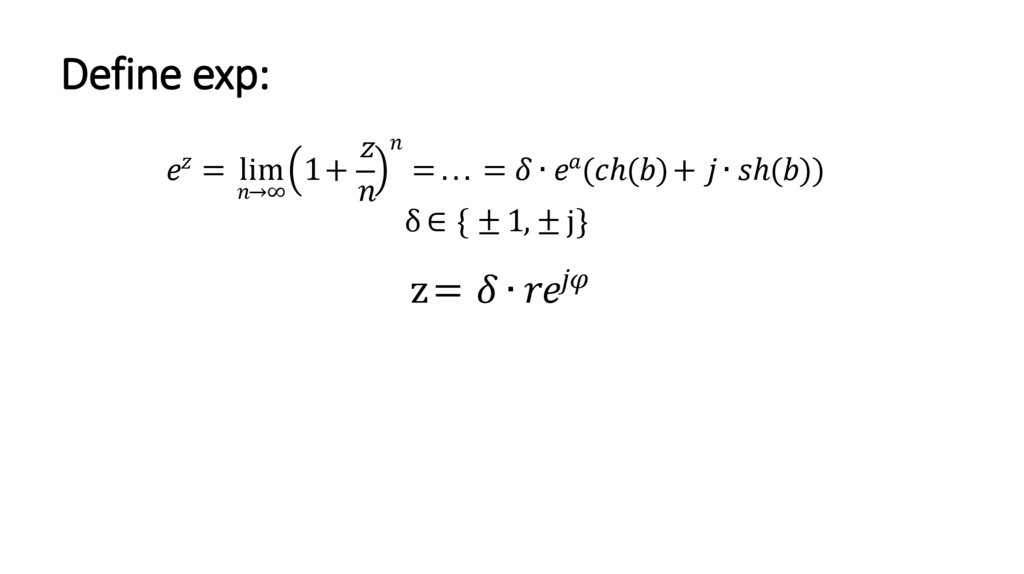


 mathematics
mathematics








