Lecture 3 Complex numbers and operations with them

2.

Complex numbers and operations with them

21.

A differential equation (DE) is an
equation that contains an unknown
function and its derivatives.
Examples:
dy
5 y 3t
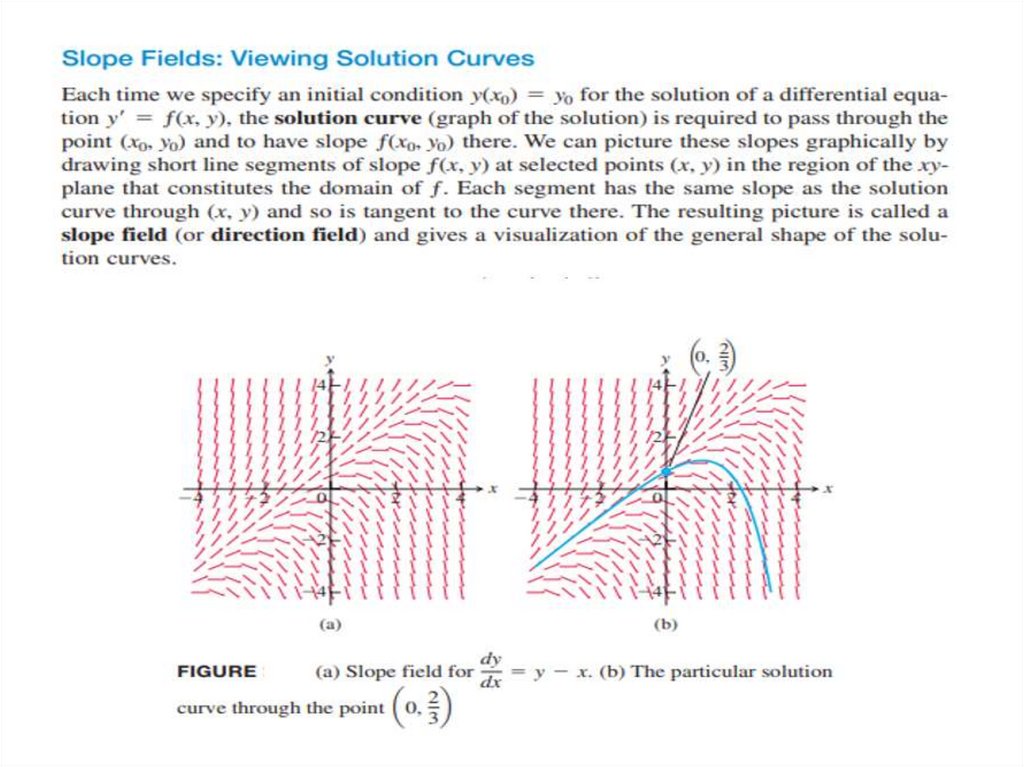
dt
2
d y
dy
7 3y 0
2
dx
dx

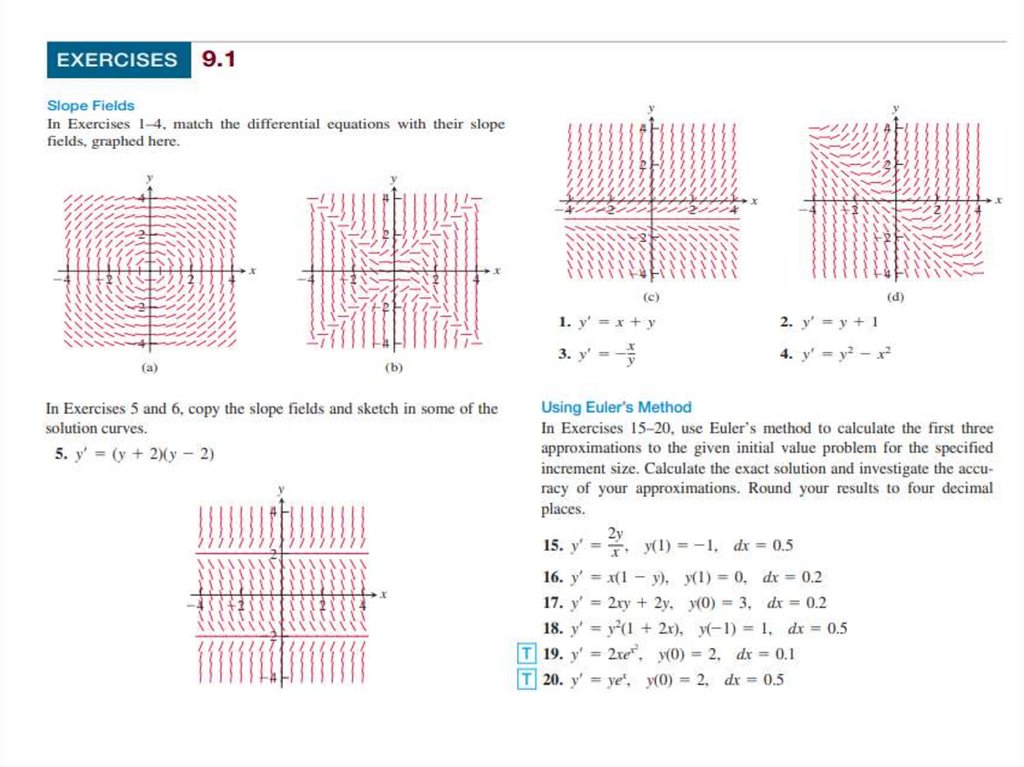
Ordinary differential equations
If the unknown function depends on
only one variable, the equation is called an
ordinary differential equation (ODE).
Examples:
1.
2.
dy
2x 3
dx
4
d 3 y dy
6y 3
3
dx
dx

23.

Partial Differential Equation
If the unknown function depends on more than
one variable, the equation is called a partial differential
equation (PDE).
Examples:
1.
2u 2u
2 0
2
x
y
u is dependent variable and x and y are independent variables, and is partial
differential equation.
2.
2 u 2 u u
2
2
t
x
t
u is dependent variable and x and t are independent variables

24.

Order of Differential Equation
The order of a differential equation is the order of the
highest derivative in the differential equation.
Differential Equation
dy
2x 3
dx
d2y
dy
3 9y 0
2
dx
dx
4
d y dy
6y 3
3
dx
dx
3
ORDER
1
2
3

25.

Degree of Differential Equation
The degree of a differential equation is the power of the highest
order of derivative term in the differential equation.
Differential Equation
Degree
d2y
dy
3 ay 0
2
dx
dx
1
4
d 3 y dy
6y 3
3
dx
dx
3
d y dy
2 3 0
dx dx
2
1
5
3

26.

Test
Differential Equation
dy
7x y
dx
y 4 y 3 y 0
3
d y dy
2 3 0
dx dx
2
5
Degree
Order

27.

Linear Differential Equation
A differential equation is linear, if
1. dependent variable and its derivatives are of degree one
2. coefficients of a term does not depend upon dependent
variable.
Example:
d2y
dy
3
9 y 0.
1.
2
dx
dx
is linear.
2.
4
d 3 y dy
6y 3
3
dx
dx
is non - linear because in 2nd term is not of degree one.

28.

1st – order differential equation
1. Derivative form:
dy
a1 x a 0 x y g x
dx
2. Differential form:
.
1 x dy ydx 0
3. General form:
dy
f ( x, y )
dx
or
dy
f ( x , y , ) 0.
dx

29.

Initial-value problem
In many physical problems we need to
find the particular solution that satisfies a
condition of the form y(x0) = y0. This is called
an initial condition.
The problem of finding a solution of the
differential equation that satisfies the initial
condition is called an initial-value problem.

30.

31.

32.

33.

34.

Equations with separable variables
The first-order differential equation
dy
f x, y
dx
is called separable provided that f(x,y)
can be written as the product of a
function of x and a function of y.

35.

To solve it :
• Separate the variables y from x, i.e., by collecting
on one side all terms involving y together with dy,
while all terms involving x together with dx are
put on the other side.
• Integrate both sides.
• If the solution can be defined explicitly, i.e., it can
be solved for y as a function of x, then do it. If not,
the solution can be defined implicitly, i.e., it
cannot be solved for y as a function of x.

36.

Suppose we can write the above equation as
dy
g ( x ) h( y )
dx
1
dy g ( x)dx
h( y )
Integrating, we get the solution as
1
h( y) dy g ( x) dx c
where c is an arbitrary constant.

37.

Examples: 1. Consider the DE
dy
y
dx
Separating the variables, we get
1
dy dx
y
Integrating we get the solution as
ln | y | x k
or
y ce , c is an arbitrary constant.
x

38.

39.

40.

41.

Linear differential equations of the first order
The first-order differential equation is said linear if
it can be brought into the form
у P ( x ) y Q ( x ).
If
if
the equation is homogeneous
the equation is nonhomogeneous

42.

The original
substitution
equation
is
transformed
by
the
y uv ( y u v uv ), u v uv P( x) uv Q( x),
where
Hence
two unknown functions.
u v u v P( x) v Q( x).
Let such that
and solving the equation
dv
dv
P( x) v 0;
P( x)dx
dx
v
We have
Substituting
v е
.
in equation yields
P( x)d x
P ( x ) dx
u Q( x) v Q( x) е
.
1

43.

Therefore
p ( x ) dx
u C Q( x)e
dx.
The general solution of the original equation
у e
p ( x ) dx
Q( x)e p ( x ) dx dx C .
E.g. Find the general solution
y 2 x y х е
х2
.

44.

Solution: Equation is linear.
u v uv 2 х uv х е
х2
u v u v 2 хv х е
y uv, y u v uv and v 2 x v 0
х2
dv
2
x2
2 x d x, ln x , e
v
To determine
u we have the equation u v х е , u е
х2
х2
x2
u х , therefore, u х d x C C.
2
Multiplying u by v , we obtain the general solution
y е
х2
x2
C .
2
хе
х2
or