Similar presentations:
Scalars, vectors and tensors
1.
CEE 451G ENVIRONMENTAL FLUID MECHANICSLECTURE 1: SCALARS, VECTORS AND TENSORS
A scalar has magnitude but no direction.
An example is pressure p.
The coordinates x, y and z of Cartesian space are scalars.
A vector has both magnitude and direction
Let ˆi, ˆj, kˆ denote unit vectors in the x, y and z direction. The hat
denotes a magnitude of unity
The position vector x (the arrow denotes a vector that is not a unit
vector) is given as
x x ˆi yˆj zkˆ
z
x
kˆ
ˆi
x
ˆj
y
1
2.
LECTURE 1: SCALARS, VECTORS AND TENSORSThe velocity vector u is given as
dx dx ˆ dy ˆ dz ˆ
u
i
j
k
dt dt
dt
dt
The acceleration vector a is given as
du du ˆ dv ˆ dw ˆ d2x d2x ˆ d2y ˆ d2z ˆ
a
i
j
k 2 2 i 2 j 2 k
dt dt
dt
dt
dt
dt
dt
dt
The units that we will use in class are length L, time T, mass M and
temperature °. The units of a parameter are denoted in brackets. Thus
[x ] L
[u] LT 1
[a ] ?
LT 2
Newton’s second law is a vectorial statement: where F denotes the
force vector and m denotes the mass (which is a scalar)
F ma
2
3.
LECTURE 1: SCALARS, VECTORS AND TENSORSThe components of the force vector can be written as follows:
F F ˆi F ˆj F kˆ
x
y
z
The dimensions of the force vector are the dimension of mass times
the dimension acceleration
[F] [Fx ] MLT 2
Pressure p, which is a scalar, has dimensions of force per unit area.
The dimensions of pressure are thus
[p] MLT 2 /(L2 ) ML 1T 2
The acceleration of gravity g is a scalar with the dimensions of (of
course) acceleration:
[g] LT 2
3
4.
LECTURE 1: SCALARS, VECTORS AND TENSORSA scalar can be a function of a vector, a vector of a scalar, etc. For
example, in fluid flows pressure and velocity are both functions of
position and time:
p p(x, t) , u u(x, t)
A scalar is a zero-order tensor. A vector is a first-order tensor. A
matrix is a second order tensor. For example, consider the stress
tensor .
xx xy xz
y x y y y z
zx
zy
zz
The stress tensor has 9 components. What do they mean? Use the
following mnemonic device: first face, second stress
4
5.
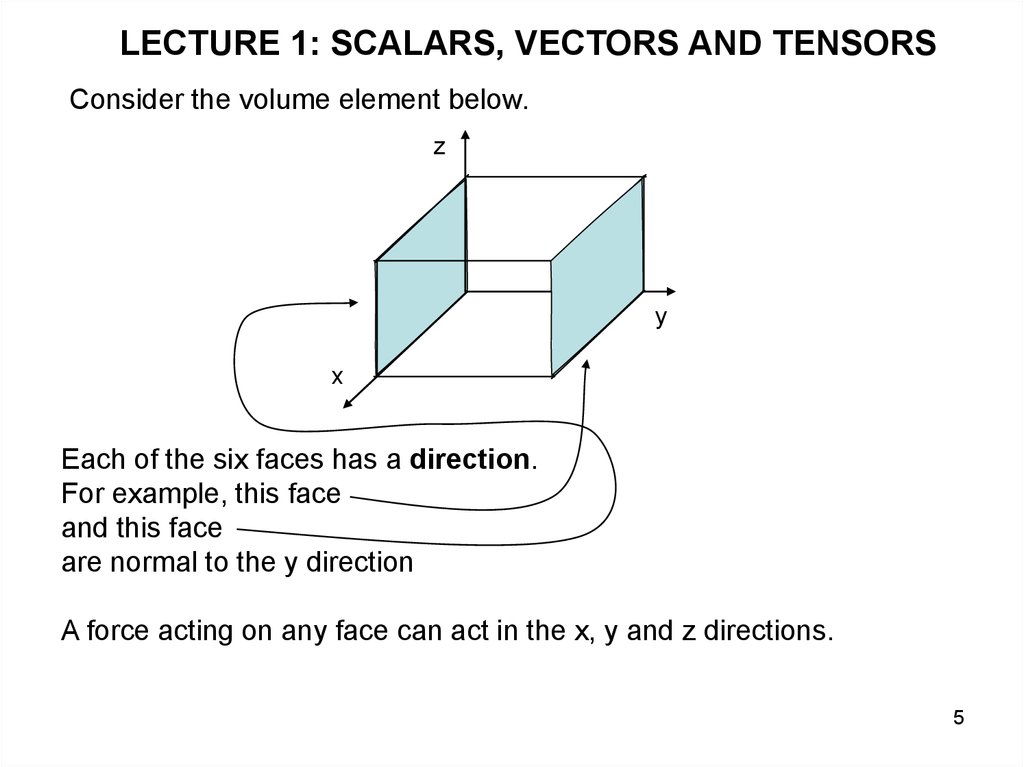
LECTURE 1: SCALARS, VECTORS AND TENSORSConsider the volume element below.
z
y
x
Each of the six faces has a direction.
For example, this face
and this face
are normal to the y direction
A force acting on any face can act in the x, y and z directions.
5
6.
LECTURE 1: SCALARS, VECTORS AND TENSORSConsider the face below.
z
yy yz
yx
y
x
The face is in the direction y.
The force per unit face area acting in the x direction on that face is the
stress yx (first face, second stress).
The forces per unit face area acting in the y and z directions on that
face are the stresses yy and yz.
Here yy is a normal stress (acts normal, or perpendicular to the face)
6
and yx and yz are shear stresses (act parallel to the face)
7.
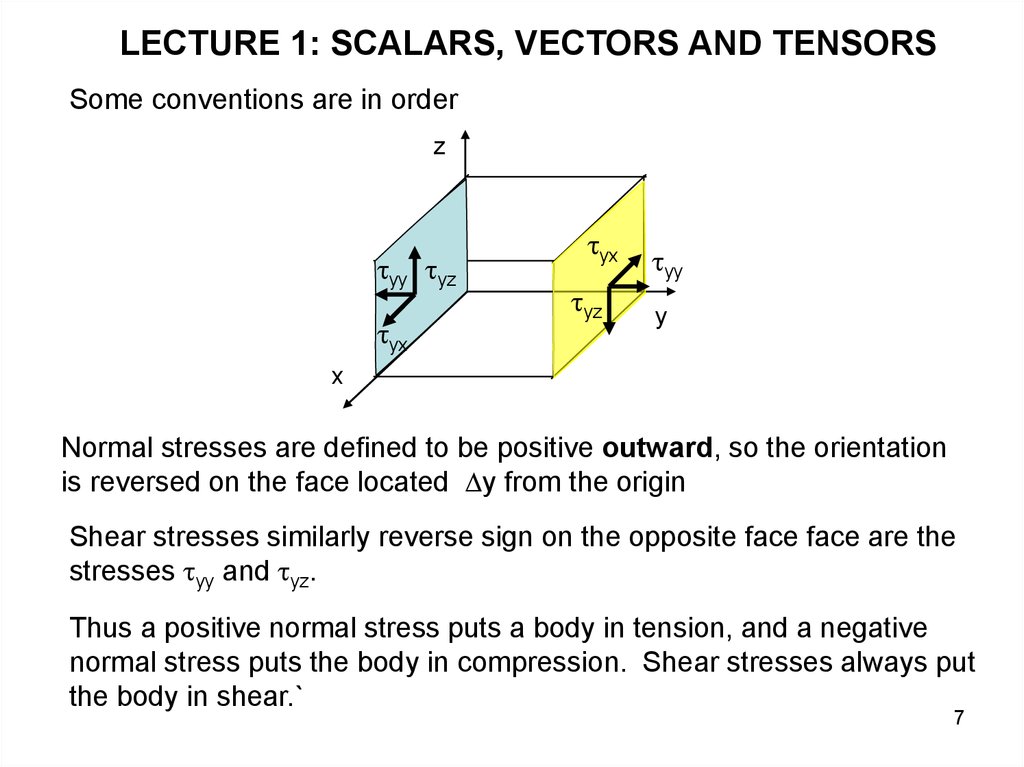
LECTURE 1: SCALARS, VECTORS AND TENSORSSome conventions are in order
z
yy yz
yx
yx
yz
yy
y
x
Normal stresses are defined to be positive outward, so the orientation
is reversed on the face located y from the origin
Shear stresses similarly reverse sign on the opposite face face are the
stresses yy and yz.
Thus a positive normal stress puts a body in tension, and a negative
normal stress puts the body in compression. Shear stresses always put
the body in shear.`
7
8.
LECTURE 1: SCALARS, VECTORS AND TENSORSAnother way to write a vector is in Cartesian form:
x x ˆi yˆj zkˆ (x, y, z)
The coordinates x, y and z can also be written as x1, x2, x3. Thus the
vector can be written as
x (x1, x 2, x 3 )
or as
x (xi ) , i 1..3
or in index notation, simply as
x xi
where i is understood to be a dummy variable running from 1 to 3.
Thus xi, xj and xp all refer to the same vector (x1, x2 and x3) , as the
index (subscript) always runs from 1 to 3.
8
9.
LECTURE 1: SCALARS, VECTORS AND TENSORSScalar multiplication: let be a scalar and A = Ai
Then
A Ai ( Ai, A2, A3 )
be a vector.
is a vector.
Dot or scalar product of two vectors results in a scalar:
A B A1B1 A2B2 A3B3 scalar
In index notation, the dot product takes the form
3
3
3
A B AiBi AkBk ArBr
i 1
k 1
r 1
Einstein summation convention: if the same index occurs twice, always
sum over that index. So we abbreviate to
A B AiBi AkBk ArBr
There is no free index in the above expressions. Instead the indices are
paired (e.g. two i’s), implying summation. The result of the dot product
9
is thus a scalar.
10.
LECTURE 1: SCALARS, VECTORS AND TENSORSMagnitude of a vector:
2
A A A Ai Ai
A tensor can be constructed by multiplying two vectors (not scalar
product):
A1B1
AiB j ( AiB j ) ,i 1..3, j 1..3 A1B2
A B
1 3
A 2B1
A 2B2
A 2B3
A 3B1
A 3B3
A 3B3
Two free indices (i, j) means the result is a second-order tensor
Now consider the expression
A i A jB j
This is a first-order tensor, or vector because there is only one free
index, i (the j’s are paired, implying summation).
Ai A jB j ( A1B1 A 2B2 A3B2 )( A1, A 2 , A3 )
That is, scalar times vector = vector.
10
11.
LECTURE 1: SCALARS, VECTORS AND TENSORSKronecker delta ij
1 0 0
1 if i j
ij
0 1 0
0 if i j
0
0
1
Since there are two free indices, the result is a second-order tensor, or
matrix. The Kronecker delta corresponds to the identity matrix.
Third-order Levi-Civita tensor.
1 if i, j,k cycle clockwise: 1,2,3, 2,3,1 or 3,1,2
ijl 1 if i, j,k cycle counterclockwise: 1,3,2, 3,2,2 or 2,1,3
otherwise
0
Vectorial cross product:
AxB ijk A jBk
One free index, so the result must be a vector.
11
12.
LECTURE 1: SCALARS, VECTORS AND TENSORSVectorial cross product: Let C be given as
C AxB
Then
ˆj
ˆi
ˆj
ˆi
kˆ
kˆ
C det A1 A 2 A 3 A1 A 2 A 3
B
B
B
B1 B2 B3
2
3
1
ˆj
ˆj ˆi
ˆj
ˆi
kˆ ˆi
kˆ ˆi
A 1 A 2 A 3 A1 A 2 A1 A 2 A 3 A1
B
B
B
B
B
B
B
B
2
3 1
2
2
3 B1
1
1
ˆj
A2
B2
A2B3 A3B2 ˆi A3B1 A1B3 ˆj A1B2 A2B1 kˆ
12
13.
LECTURE 1: SCALARS, VECTORS AND TENSORSVectorial cross product in tensor notation:
Ci ijk A jBk
Thus for example
=1
= -1
=0
C1 1jk A jBk 123 A 2B3 132 A3B2 111A1B1
A2B3 A3B2
a lot of other terms that
all = 0
i.e. the same result as the other slide. The same results are also
obtained for C2 and C3.
The nabla vector operator :
ˆ
ˆ
ˆ
i
j
k
x1
x 2
x 3
or in index notation
x i
13
14.
LECTURE 1: SCALARS, VECTORS AND TENSORSThe gradient converts a scalar to a vector. For example, where p is
pressure,
p ˆ p ˆ p ˆ
grad(p) p
i
j
k
x1
x 2
x 3
or in index notation
p
grad(p)
x i
The single free index i (free in that it is not paired with another i) in the
above expression means that grad(p) is a vector.
The divergence converts a vector into a scalar. For example, where u
is the velocity vector,
u u
u
u u
div(u) 1 2 3 i k
x1 x 2 x 3 x i x k
Note that there is no free index (two i’s or two k’s), so the result is a
scalar.
14
15.
LECTURE 1: SCALARS, VECTORS AND TENSORSThe curl converts a vector to a vector. For example, where u is the
velocity vector,
ˆi
curl(u) xu
x1
u1
ˆj
x 2
u2
kˆ
x 3
u3
u3 u2 ˆ u1 u3 ˆ u2 u1 ˆ
i
j
k
x 2 x 3 x 3 x1 x1 x 2
or in index notation,
uk
curl(u) ijk
x j
One free index i (the j’s and the k’s are paired) means that the result is a
vector
15
16.
LECTURE 1: SCALARS, VECTORS AND TENSORSA useful manipulation in tensor notation can be used to change an index
in an expression:
iju j ui
This manipulation works because the Kronecker delta ij = 0 except when
i = j, in which case it equals 1.
16














 mathematics
mathematics








