Признаки равенства треугольников. Урок 2

1.

2.

№ 65 Найдите смежные углы hk и kl, если
(а)
меньше
kl на 40о.
Дано:
k
hk и kl смежные
kl –
x
hk
x + 40
h
Найти:
l
Решение:
x + (x + 40) = 180
x = 70
Ответ: 70о и 110о
hk = 70о
kl = 110о
hk = 40о
hk и
kl

3.

№ 65 Найдите смежные углы hk и kl, если
(г)
=3
hk =
kl.
Дано:
k
3x
h
hk и kl смежные
hk = 3
x
l
Найти:
Решение:
x + 3x = 180
hk = 135о
x = 45
kl = 45о
Ответ: 135о и 45о
hk и
kl
kl

4.

№ 65 Найдите смежные углы hk и kl, если
(д)
hk :
kl = 5 : 4.
k
Дано:
hk и kl смежные
hk :
5x
4x
h
l
Найти:
Решение:
5x + 4x = 180
hk = 100о
x = 20
kl = 80о
Ответ: 100о и 80о
kl = 5 : 4
hk и
kl

5.

№ 69 Найдите неразвернутые углы, образован(а)
ные при пересечении двух прямых, если
сумма двух из них равна 114о.
Дано:
2
1
Найти:
3
4
Решение:
1=
3 = 114о : 2 = 57о
2=
4 = 180о – 57о = 123о
Ответ: 57о, 123о, 57о, 123о
1+
3 = 114о
1,…,
4

6.

09.09.2024
К л а с с н а я р а б о т а.
Признаки равенства
треугольников.

7.

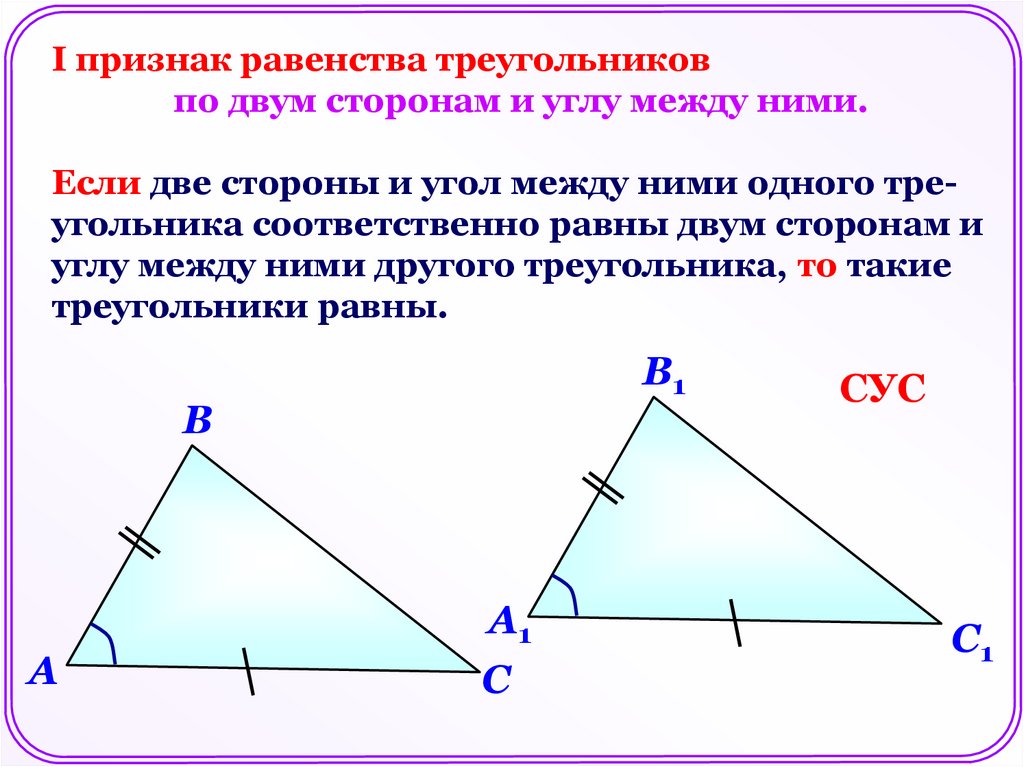
I признак равенства треугольников
по двум сторонам и углу между ними.
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и
углу между ними другого треугольника, то такие
треугольники равны.
В1
В
А
А1
С
СУС
С1

8.

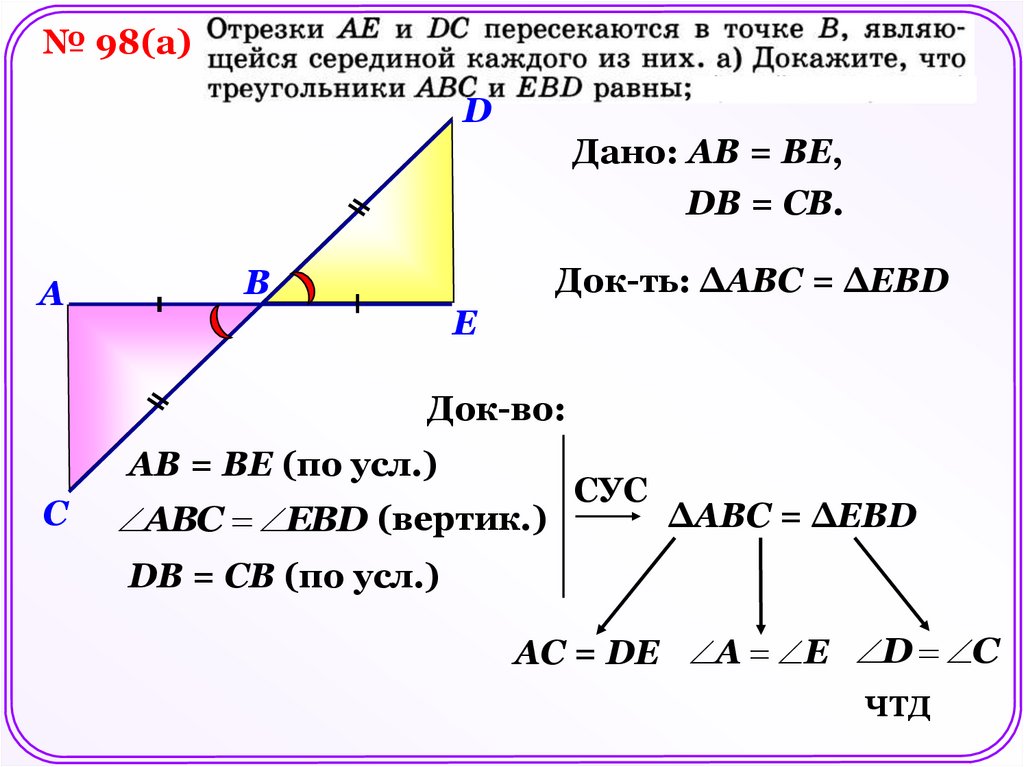
№ 98(а)
D
Дано: АВ = ВЕ,
DВ = СВ.
A
Док-ть: ΔАВС = ΔЕВD
В
Е
Док-во:
АВ = ВЕ (по усл.)
С
АВС ЕВD (вертик.)
СУС
ΔАВС = ΔЕВD
DВ = СВ (по усл.)
АС = DЕ А Е D C
ЧТД

9.

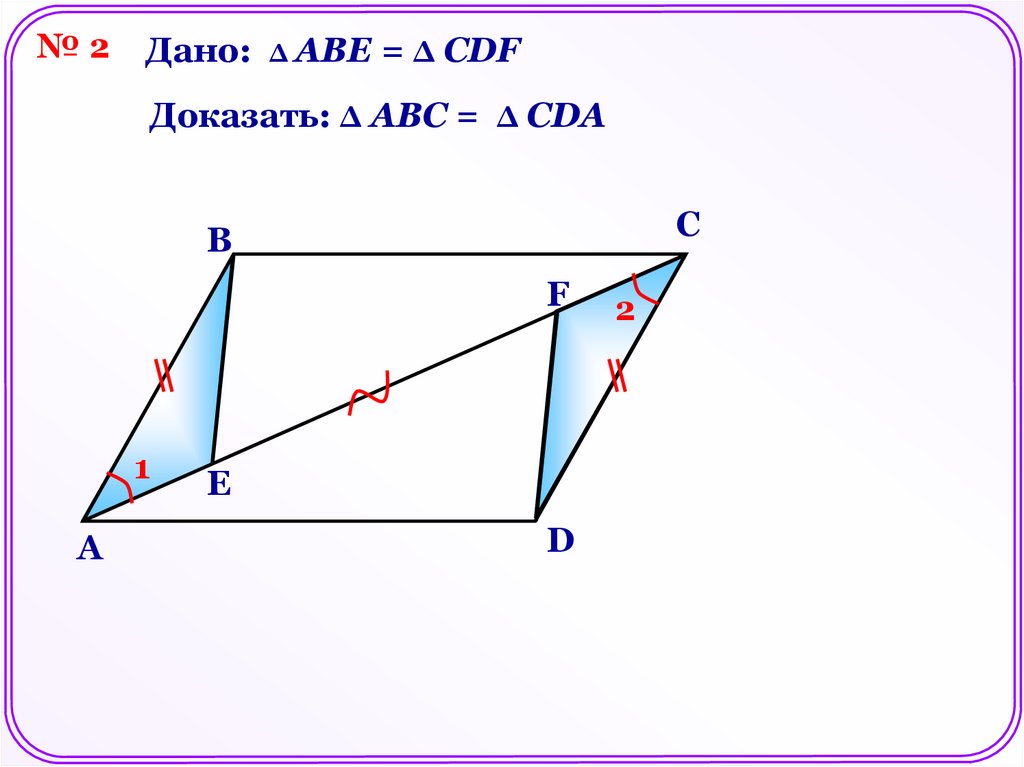
№2
Дано: Δ АВЕ = Δ СDF
Доказать: Δ АВC = Δ CDA
C
B
F
1
А
E
D
2

10.

№2
B
C
F
2
Дано: Δ АВЕ = Δ СDF
Док-ть: Δ АВC = Δ CDA
1
E
А
D
Док-во:
АВ = CD
1) ΔАВЕ = ΔСDF (по усл.)
2) АВ = CD (п.1)
1 2 (п.1)
АС = АС
СУС
1 2
ΔАВС = ΔСDА
ЧТД

11.

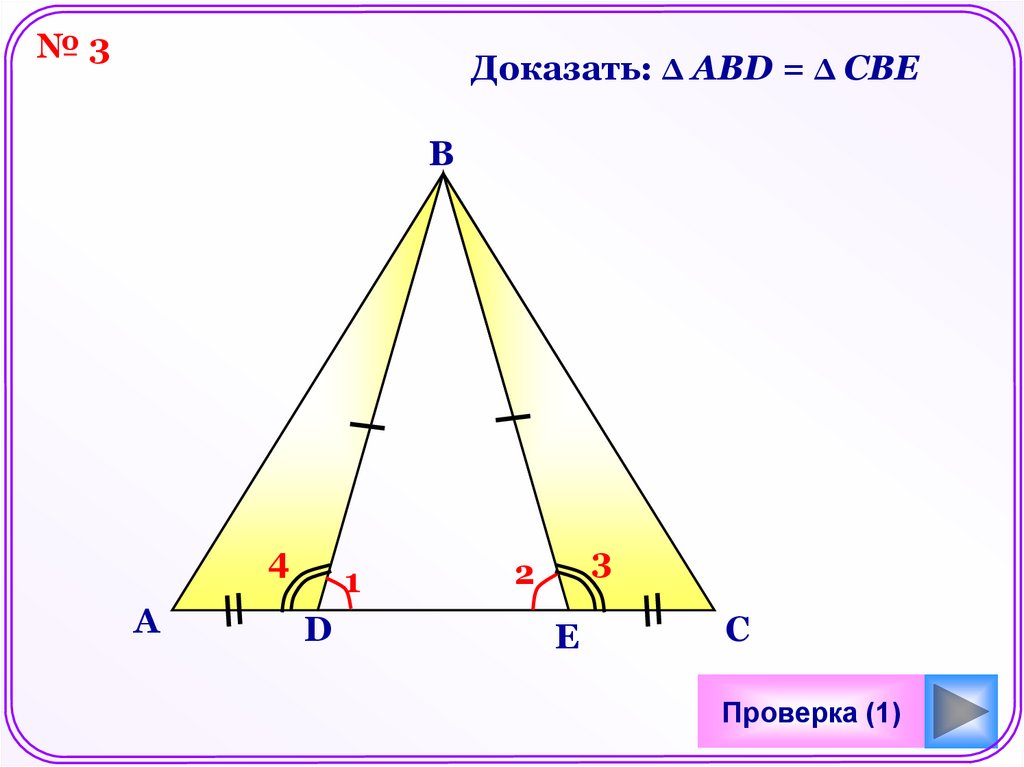
№3
Доказать: Δ АВD = Δ CBE
В
4
А
1
D
3
2
E
С
Проверка (1)

12.

В
№3
Дано: АD = CЕ,
BD = BЕ,
1 2
Док-ть: ΔАВD = ΔCBЕ
4
А
1
D
Док-во:
3
2
E
С
АD = CE (по усл.)
3 4 (смежные с равными)
ВD = ВЕ (по усл.)
СУС
ΔАВD = ΔСВЕ
ЧТД

13.

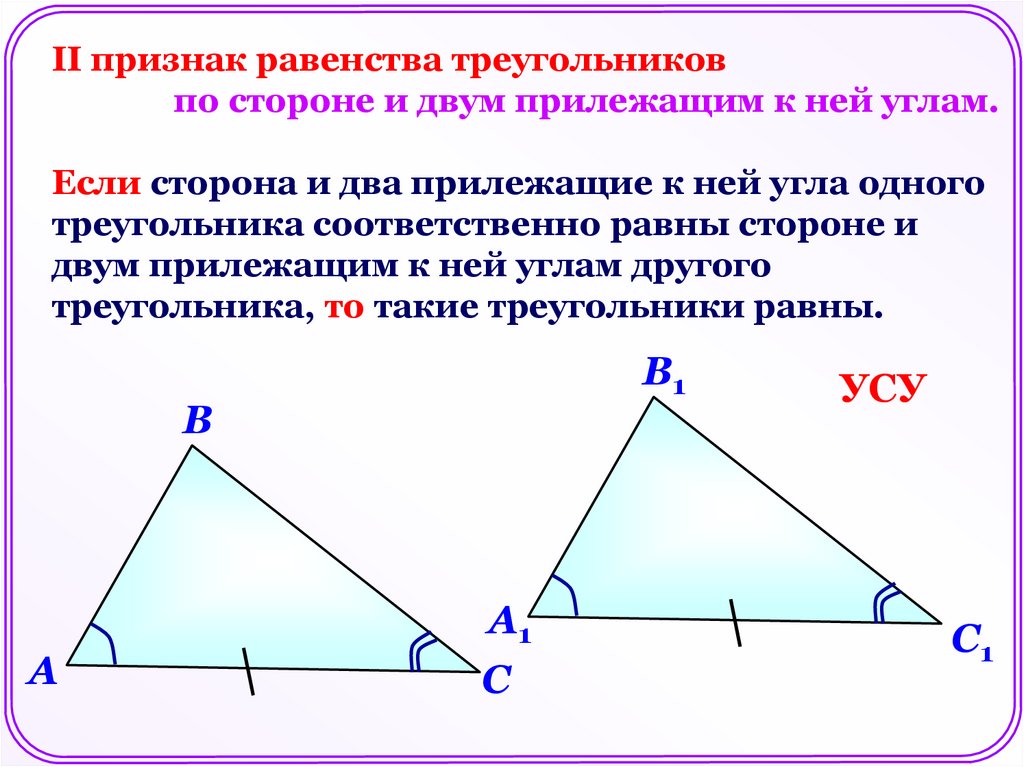
II признак равенства треугольников
по стороне и двум прилежащим к ней углам.
Если сторона и два прилежащие к ней угла одного
треугольника соответственно равны стороне и
двум прилежащим к ней углам другого
треугольника, то такие треугольники равны.
В1
В
А
А1
С
УСУ
С1

14.

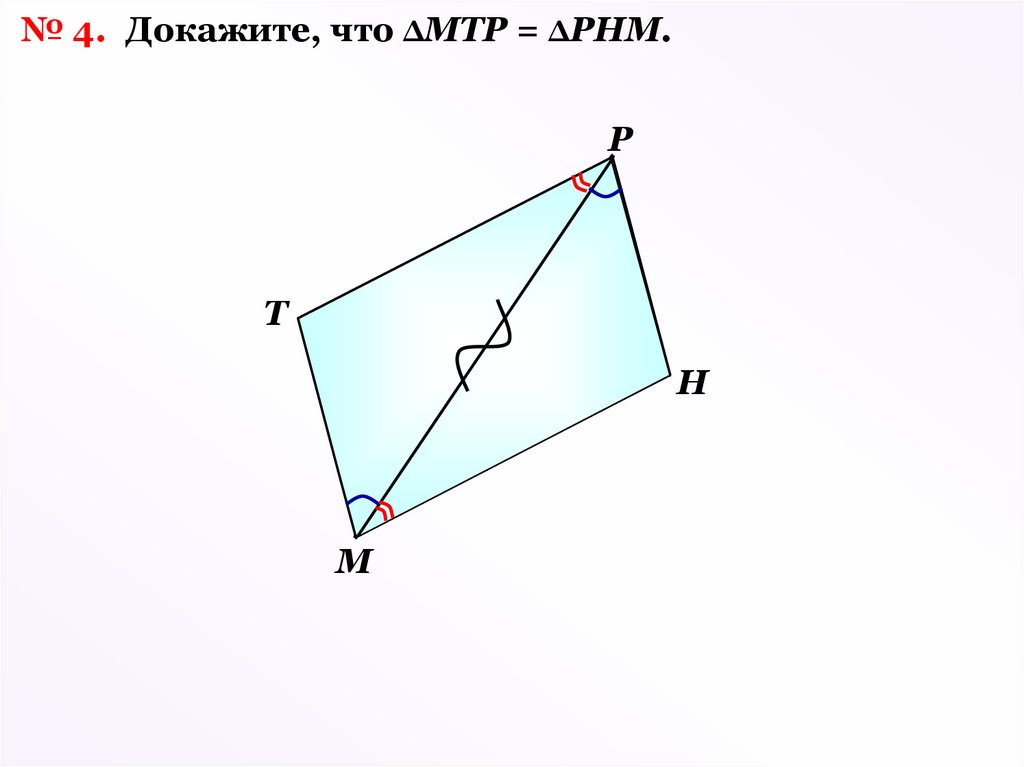
№ 4. Докажите, что ΔМТР = ΔРНМ.
Р
Т
Н
М

15.

№ 4. Докажите, что ΔМТР = ΔРНМ.
Р
Дано: 1 2, 3 4
3 2
Док-ть: ΔМТР = ΔРНМ
Т
Н
1 4
М
1 2 (по усл.)
МР = МР
Док-во.
УСУ
ΔМТР = ΔРНМ
3 4 (по усл.)
чтд

16.

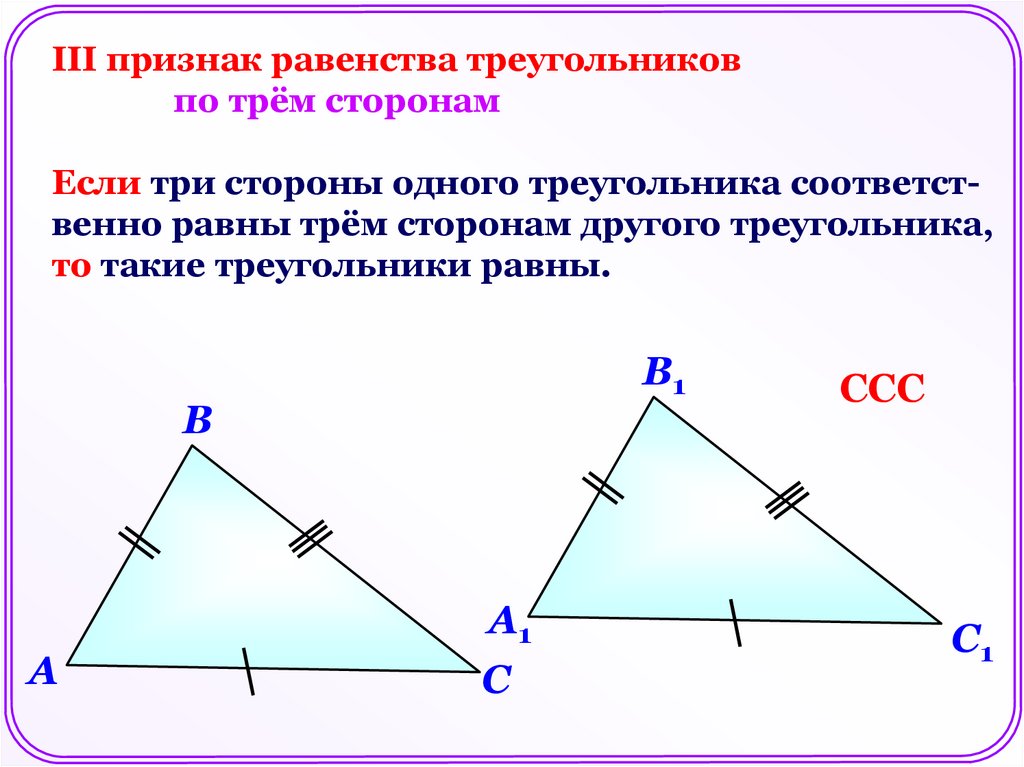
III признак равенства треугольников
по трём сторонам
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника,
то такие треугольники равны.
В1
В
А
А1
С
ССС
С1