Similar presentations:
Квадратные уравнения. Их виды и решений. Алгебра. 8 класс
1.
Презентацияурока
Алгебра 8 класс
Квадратные
их виды и
решений
2
уравнения
методы
ах вх с 0
2
х +pх+q=0
Учитель математики
Ильинова Вера Ивановна
2.
Девизурока
Пусть каждый день и каждый час
Вам новое добудет.
Пусть добрым будет ум у вас,
А сердце умным будет.
Самуил Маршак
3.
Повторение :1. Какое название имеет уравнение второй степени?
2. От чего зависит количество корней квадратного
уравнения?
3. Когда начался XXI век?
4. Сколько корней имеет квадратное уравнение,
если D больше 0?
5. Что значит решить уравнение?
6. Как называется квадратное уравнение, у которого
первый коэффициент - 1?
7. Сколько раз в году встает солнце?
8. Сколько корней имеет квадратное уравнение,
если дискриминант меньше 0?
9. Есть у любого слова, у растения и может быть у
уравнения?
4.
Историческая справкаКвадратные уравнения уже умели решать
математики и в древнем Вавилоне и древнем
Египте. Сохранились папирусы с решениями
некоторых задач , на составление квадратных
уравнений .
Правила их решений схожи с теми , которыми
пользуемся мы сейчас
Значительных успехов достигли математики
древней Греции и конечно же Диофант
Нередко он упоминается как «отец алгебры». Автор
«Арифметики» — книги, посвящённой нахождению
положительных рациональных решений неопределён
ных уравнений.
Диофант
Александрийский
Диофант был первым греческим математиком, который рассматривал
дроби наравне с другими числами. Диофант также первым среди античных
учёных предложил развитую математическую символику, которая
позволяла формулировать полученные им результаты в достаточно
компактном виде.
5.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.«Обезьянок резвых стая
Всласть поевши, развлекалась
Их в квадрате часть восьмая
На поляне забавлялась
А двенадцать по лианам
Стали прыгать, повисая
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?»
Соответствующее задаче уравнение:
x2 - 64x = - 768
и, чтобы дополнить левую часть этого уравнения до
квадрата, прибавляет к обеим частям 322, получая
затем:
x2 - б4х + 322 = -768 + 1024,
(х - 32)2 = 256,
х - 32= ±16,
x1 = 16, x2 = 48.
гениальное решение квадратного уравнения
Памятник индийскому математику
гениальным математиком
БРАХМАГУПТЕ
6.
Полные квадратные уравнения:2
ах вх с 0
где a, b, c - числовые коэффициенты,
причём а ≠ 0,
х – переменная
например :
5х2 + 8х – 4 = 0
7х2 + 6х – 1 = 0
2х2 – х + 11 = 0
3х2 + 2х = 16
7.
Составьте квадратное уравнение, еслиа = 4, в = -5, с = -6.
а = -2, в = 4, с = 1.
а = 3, в = -2, с = 8.
а = -3, в = -4, с = -2.
8.
Составьте квадратное уравнение, еслиа = 4, в = -5, с = -6.
4х2 - 5х – 6 = 0
а = -2, в = 4, с = 1.
-2х2 + 4х + 1 = 0
а = 3, в = -2, с = 8.
3х2 - 2х + 8 = 0
а = -3, в = -4, с = -2.
-3х2 - 4х - 2 = 0
9.
Неполные квадратные уравнения:ах вх 0
Коэффициент С = 0
ах с 0
Коэффициент в = 0
ах 0
Коэффициент в = 0 и С = 0
2
2
2
Если в квадратном уравнении
ах2 + вх + с = 0 хотя бы один из
коэффициентов в или с равен нулю,
то такое уравнение называют
неполным квадратным уравнением.
10.
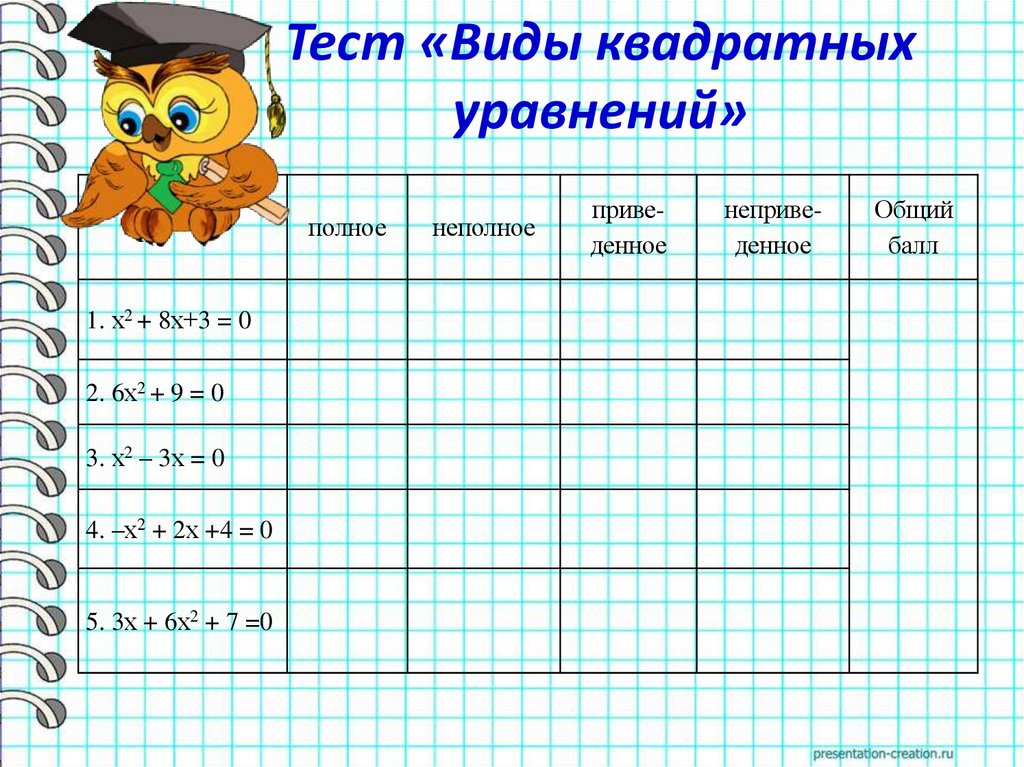
Тест «Виды квадратныхуравнений»
полное
1. х2 + 8х+3 = 0
2. 6х2 + 9 = 0
3. х2 – 3х = 0
4. –х2 + 2х +4 = 0
5. 3х + 6х2 + 7 =0
неполное
приведенное
неприведенное
Общий
балл
11.
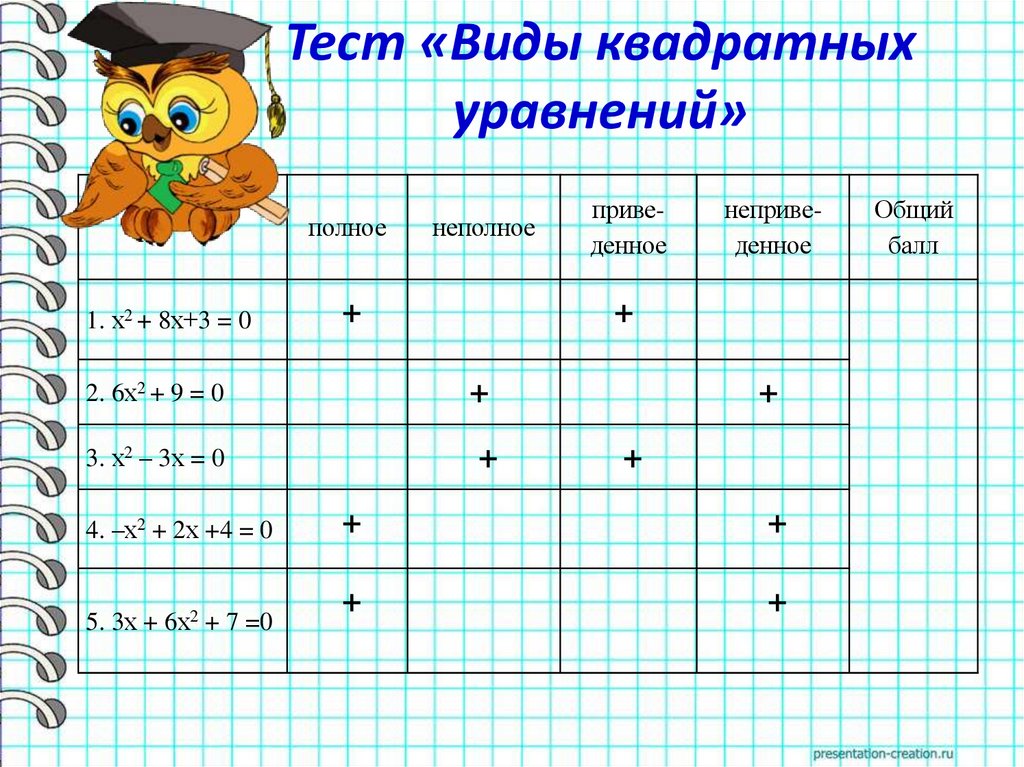
Тест «Виды квадратныхуравнений»
полное
1. х2 + 8х+3 = 0
неполное
+
+
3. х2 – 3х = 0
+
5. 3х + 6х2 + 7 =0
неприведенное
+
2. 6х2 + 9 = 0
4. –х2 + 2х +4 = 0
приведенное
+
+
+
+
+
+
Общий
балл
12.
Дискриминант2
D = в – 4ас
Дискриминант обозначается латинской буквой D
D = в2 – 4ас ; D > 0 Уравнение имеет 2 корня
D = в2 – 4ас ; D= 0 Уравнение имеет 1 корень
D = в2 – 4ас ; D < 0 Уравнение не имеет корней
Термин ДИСКРИМИНАНТ образован от латинского
discrimino — «разбираю», «различаю». Ввел его
английский математик Джеймс Джозеф Сильвестр
13.
Приведите к стандартномувиду
1. х + 5х2 = 6
2. 4х – 5 + x2 = 0
3. (2 - 5х)2 = 9
14.
Приведите к стандартномувиду
1. х + 5х2 = 6
5х2 + х - 6 = 0
2. 4х – 5 + x2 = 0
х2 + 4х - 5 = 0
3. (2 - 5х)2 = 9
25х2 – 20х – 5 = 0
15.
23х + 32х +80 = 0
2
100х -160х +63= 0
х2 – 64= 0
2
-х + 8х = 0
х2 -12х = 0
2
6х = 0
2
х + 6х +3 = 0
16.
ЦМ
Л
Ы
О
Д
6,0,0 3,32,80 1,0,-64 1,6,3 100,-160,63 1,-12,0
О
-1,8,0
17.
Самостоятельная работаРешите уравнение:
1) 5х2 – 20х = 0;
2) 5х2 + 3х – 2 = 0;
3) х2 + 10х + 9 = 0;
4) 4х2 – 16 = 0;
5) х2 -14х + 49 = 0.
18.
Самостоятельная работаРешите уравнение:
1) 5х2 – 20х = 0;
х1 = 0; х2 = 4
2) 5х2 + 3х – 2 = 0;
х1 = -1; х2 = -9
3) х2 + 10х + 9 = 0;
Корней нет
4) 4х2 – 16 = 0;
х1 = -2; х2 = 2
5) х2 -14х + 49 = 0.
х=7
19.
Подсчитайте сумму баллов,заработанных в течение урока.
Критерии оценивания:
25 – 31 балл – “5”.
16 - 24– баллов – “4”.
10 - 15 баллов – “3”.
20.
Домашнее задание :Выучить определения и формулы вычисления
корней квадратных уравнений
Решить квадратные уравнения:
1) 6х2 – 2х + 7 = 0
2) 1,2х2 +5 – 3x = 0
3) 4x2 – 15x = 0
4) 6x2 - 96 = 0
5) 14x – 3x2 + 19 = 0
6) 5x2 – 4x = 7
2. Найдите длины сторон прямоугольника, периметр
которого равен 38 см, а площадь 84 см2.
3. Один из корней уравнения х2 +11х +q = 0 равен – 7.
Найдите второй корень и число q.
21.
Рефлексия :Продолжи фразы:
Мне было интересно…
Мы сегодня разобрались…
Я сегодня понял, что…
Мне было трудно…
Мне понравилось …
Завтра я хочу на уроке…
Я решал эти непонятные уравнения…
Я добросовестно работал…
Я преумножил свои знания!...












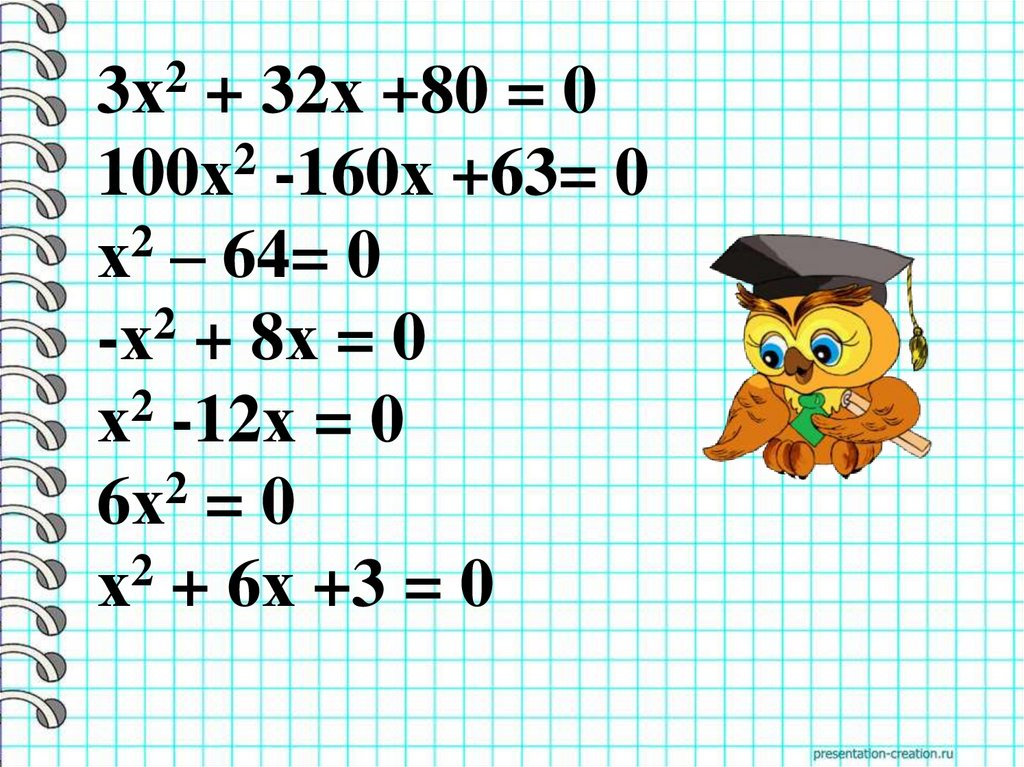







 mathematics
mathematics








