Similar presentations:
Кинетические явления в условиях стационарной неравновесности. Глава 3
1.
Курс лекцийФизика полупроводников и
полупроводниковых приборов
Глава 3. КИНЕТИЧЕСКИЕ ЯВЛЕНИЯ В УСЛОВИЯХ
СТАЦИОНАРНОЙ НЕРАВНОВЕСНОСТИ
1
2.
3.1. Дрейфовая и диффузионная электропроводностиДрейфовая электропроводность
q
a *E
mn
V a n
q
Vср * n E = μn E
mn
q
n * п
mn
+E -
EC
n
EV
EC
EV
n
p
E
Vn
Jn
E
Vp
Jp
p
j jn j p q( n n p p ) E
µ – подвижность носителей заряда
2
3.
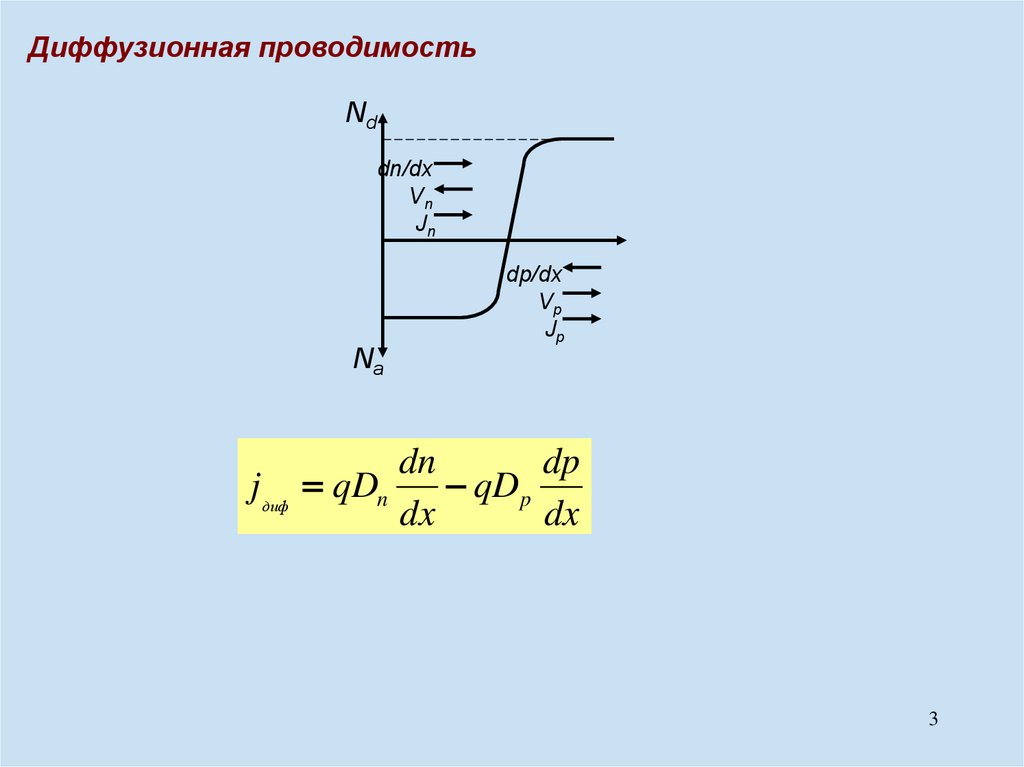
Диффузионная проводимостьNd
n:
dn/dx
Vn
Jn
p:
dn/dx
Vn
Jn
dp/dx
Vp
Jp
dp/dx
Vp
Jp
Na
dn
dp
j диф qDn
qD p
dx
dx
3
4.
dndx
dp
j p j pдр j pдиф q p p qD p
dx
jn jnдр jnдиф q n n qDn
Dn 38см 2 / с
D p 13см 2 / с
kT
Dn
n
q
kT
Dp
p
q
4
5.
dnjn jnдр jnди ф q n n qDn
0
dx
kT
Dn
n
q
kT
Dp
p
q
5
6.
67.
78.
kTDn
n
q
kT
Dp
p
q
8
9.
kTDn
n
q
kT
Dp
p
q
9
10.
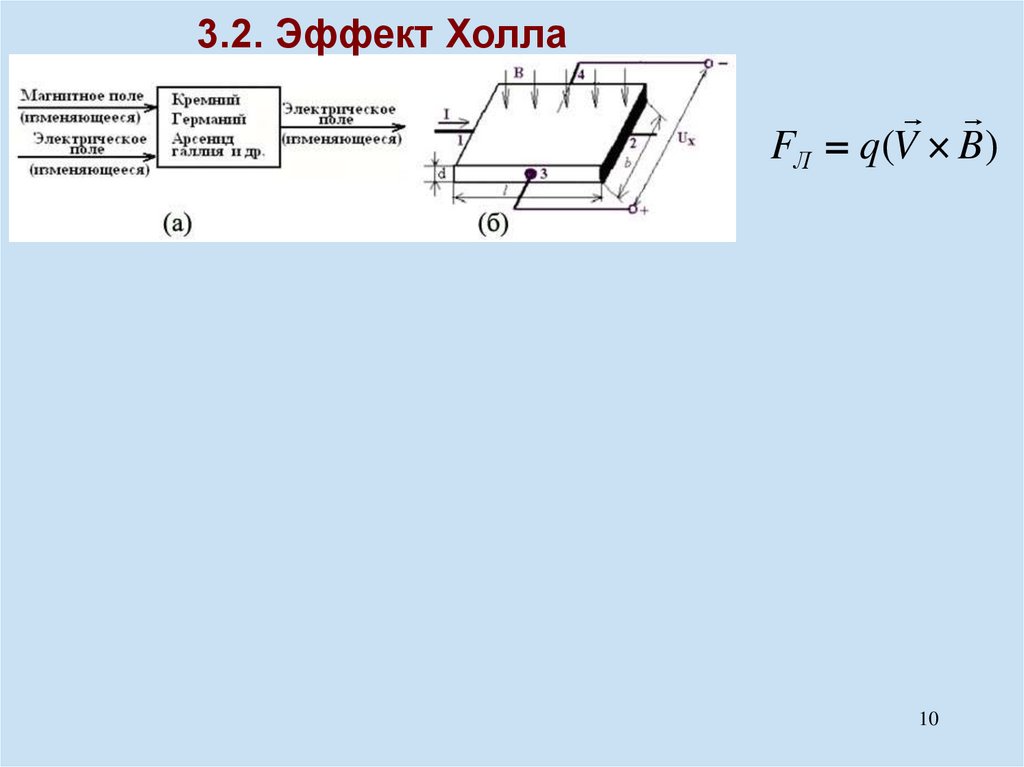
3.2. Эффект ХоллаFЛ q(V B)
10
11.
FЛ q (V B)11
12.
1213.
U X RXJ B
d
13
14.
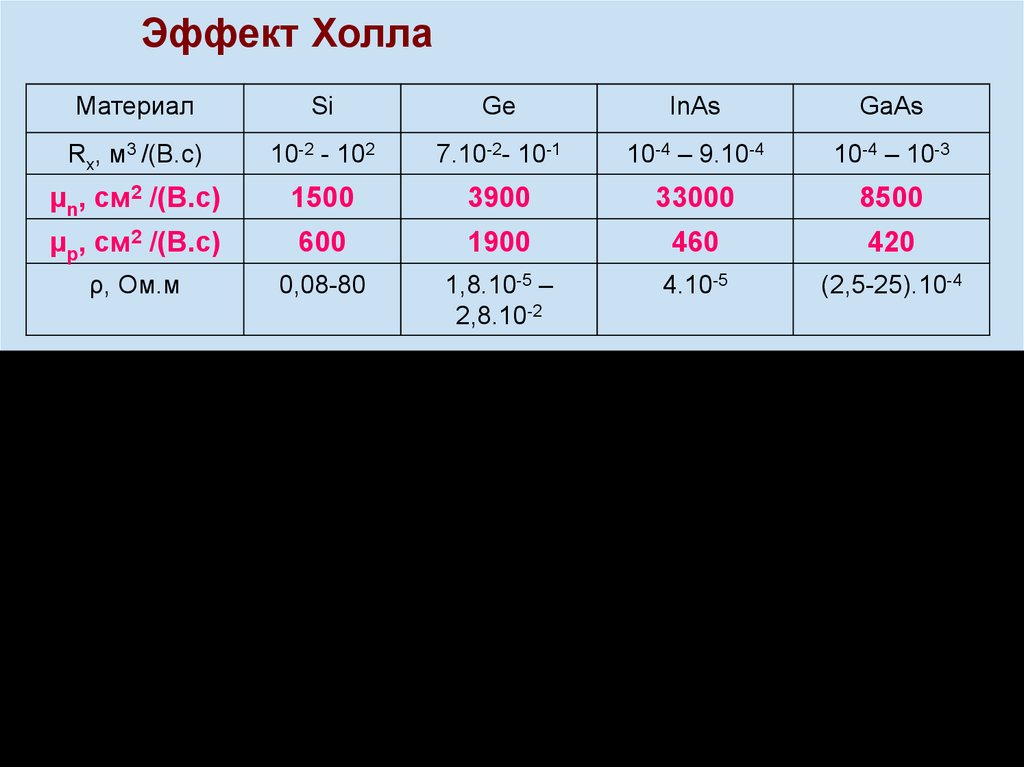
Эффект ХоллаМатериал
Si
Ge
InAs
GaAs
Rx, м3 /(B.c)
10-2 - 102
7.10-2- 10-1
10-4 – 9.10-4
10-4 – 10-3
μn, см2 /(B.c)
1500
3900
33000
8500
μp, см2 /(B.c)
600
1900
460
420
ρ, Ом.м
0,08-80
1,8.10-5 –
2,8.10-2
4.10-5
(2,5-25).10-4
14
15.
3.3. Механизмы рассеяния носителей зарядаИзменение состояния свободных носителей
заряда вследствие их взаимодействия с
отклонениями
от
периодичности
поля
кристаллической решетки называют рассеянием
носителей заряда.
В классической физике изменение состояния
можно трактовать как искривление траектории
движущегося
электрона. В квантовой –
переход из одного места в зоне Бриллюэна в
другое.
15
16.
3.3. Механизмы рассеяния носителей зарядаσ – эффективное сечение рассеяния на
n1 = σ N V0 n0 =P n0
одном рассеивающем центре;
n1 – количество электронов, рассеянных в
n1
единицу времени;
σ
n0 – количество свободных электронов;
N – количество центров рассеяния;
n0, V0
V0– средняя тепловая скорость эл-нов;
N
P – вероятность рассеяния одного
электрона в единицу времени;
τ – время свободного пробега (время Схема рассеяния носителей
жизни);
Ln – длина свободного пробега электрона.
n1
N n0 V0
P
N V0
Эффективное сечение рассеяния есть отношение
числа электронов,
1
Ln
1
1
удаленных
рассеяния
на одном центре в
Ln
n из пучка в результате
16
Nк плотности
V0 V0 падающего пучка
N
единицу P
времени
17.
A. Вакансии (V), междоузельные атомы (I)Эффективность рассеяния на таких дефектах, как
вакансии, междоузельные атомы определяется сечением
места. которое они занимают. Т.е. за σ можно принять
площадь квадрата со стороной, равной постоянной
решетки а. Типичное значение а для полупроводников – а
= 5Ả = 5∙10-8 см. Тогда: σI = (5∙10-8)2 ≈ 3∙10-15см2.
Термодинамически равновесная концентрация точечных
дефектов (I, V) при Ткомн составляет: NI~1016 см-3. Тогда LnI
= 1/(3∙10-15 ∙ 1016 )= 3∙10-2 см = 300 мкм.
Схема рассеяния на I или V
17
18.
Б. Ионы примеси (q)Для ионов примеси можно считать, что диаметр
кулоновского взаимодействия распространяется
на расстояние в 10 раз больше диаметра
нейтрального атома, т.е. σq = (10∙5∙10-8)2 ≈ 3∙10-13
см2. Если Nq=1016cм-3, тогда Lnq = 3∙10-4 см = 3
мкм.
dq
Схема рассеяния на ионах
примеси
18
19.
В. Дислокации (d)Дислокации
–
линейные
дефекты,
распространяющиеся в кристалле на большие расстояния
(типично – диапазон мм–см). Предположим, дислокация
имеет длину 0.1см, а диаметр – сотня периодов решетки. В
этом случае площадь ее сечения - σd = 0.1∙100∙5∙10-8 ≈ 3∙10-7
см2. НО! Плотность дислокаций как правило низка!!!
Коллектор бип. тр-ра: Nd=104 см-3 Ld ~ 200 см;
База бип. тр-ра:
Nd=106 см-3 Ld ~ 2 см;
Эмиттер бип. тр-ра: Nd=108 см-3 Ld ~ 200 мкм
19
20.
Г. Фононы (ph)Эффективное сечение рассеяния на тепловых колебаниях
решетки определяется площадью сечения области, которую
занимает колеблющийся атом за вычетом площади сечения
самого атома (заштрихована).
Диаметр атома – d = 10-8 см; типичная амплитуда
колебаний – r = 0.05 нм = 5∙10-9 см; тогда σph = (d+r)2-d2 ≈ 2rd ~
10-16 см-2. Это значительно меньше, чем у других видов
рассеяния!!! НО! Число фононов (~ атомов решетки) велико
(Nph~ n∙1022 см-3)! Откуда следует:
Lph = (10-16 ∙ 5∙1022)-1 ~ 2∙10-7 см = 0.002 мкм = 20Ả
d
Схема
фононах
r
рассеяния
20
на
21.
ИТАК:1. V, I:
LnI = 300 мкм
2. Ионы примеси: Lnq = 3 мкм
3. Дислокации: Ld= 200 мкм - 200 см
4. Фононы (ph)
Lph = 20Ả
21
22.
3.3.1. Зависимость подвижности от температурыq
m*
V f (T )
Ln f (T )
Ln
V
q Ln
m* V
3/2kT~mV2/2;
1
Ln
N
V~ T
Т.е. зависит от механизма
рассеяния!!!
22
23.
3.3.1. Зависимость подвижности от температурыРассеяние на тепловых колебаниях решетки
1
FБ ( E )
e
kT
1
3/2kT~mV2/2;
e
kT
kT
1 Nph ~ FБ(E)~
~T
kT
V~ T
q Ln
m* V
Ln
ph ~
1
N ph
Ln ~
1
T
3/ 2
23
1
T
24.
3.3.1. Зависимость подвижности от температурыРассеяние на тепловых колебаниях решетки
1
FБ ( E )
e
kT
1
3/2kT~mV2/2;
e
kT
kT
1 Nph ~ FБ(E)~
~T
kT
1
Ln
N ph
1
Ln ~
T
V~ T
Ln ~
1
T
q Ln
Итак:
m* V V ~ T
ph ~
1
T
3/ 2
24
25.
Рассеяние на ионизованной примесиИз кин. уравнения Больцмана L ~ V4
n
3
3/ 2
q ~T
q
~V
1
1
ph
1
q
преобладает рассеяние на:
aT
3/ 2
bT
3 / 2
μ
ионах примеси фононах
~T-3/2
~T3/2
T T
T 3/ 2
3
aT b aT 3 b
Tmax
T
25
26.
Правило сложения подвижностейn1 = σ N V0 n0 =P n0
σ – эффективное сечение рассеяния на
n1
одном рассеивающем центре;
σ
P – вероятность рассеяния одного
электрона в единицу времени;
n0, V0
N
τ – время свободного пробега (время
жизни);
Ln – длина
электрона.
свободного
пробега
Схема рассеяния носителей
Различные механизмы рассеяния действуют независимо друг от
друга. Отсюда следует, что вероятности различных процессов
рассеяния суммируются, т.е. P = ∑Pi .
1
1
1
1
1
Поскольку



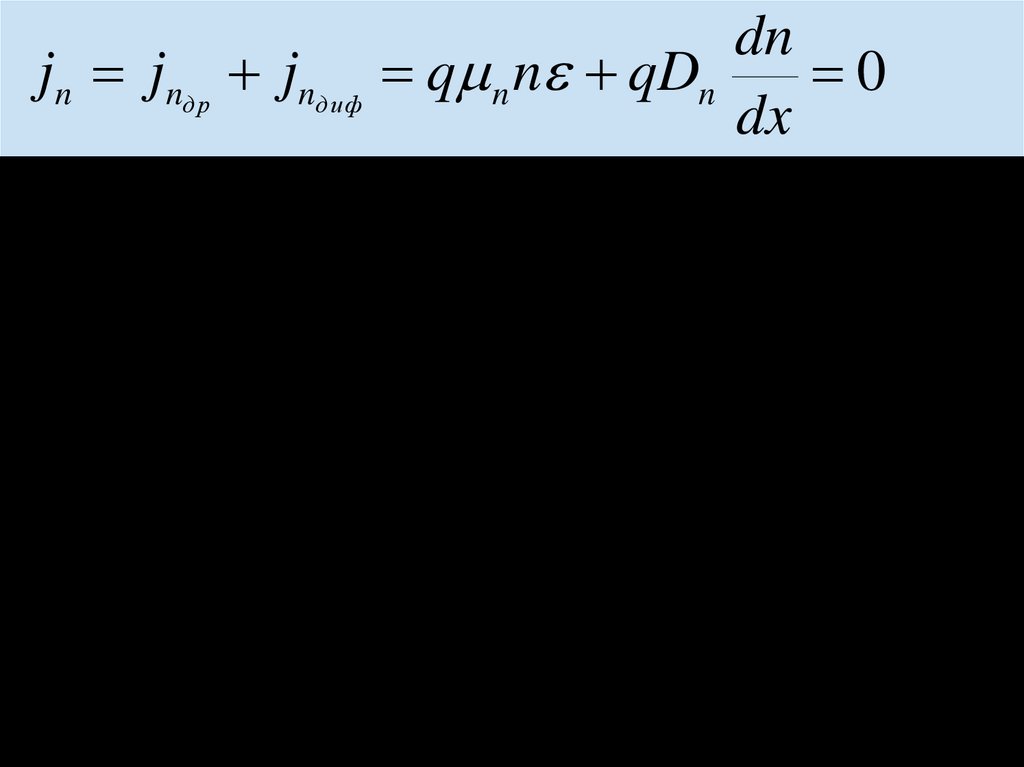
























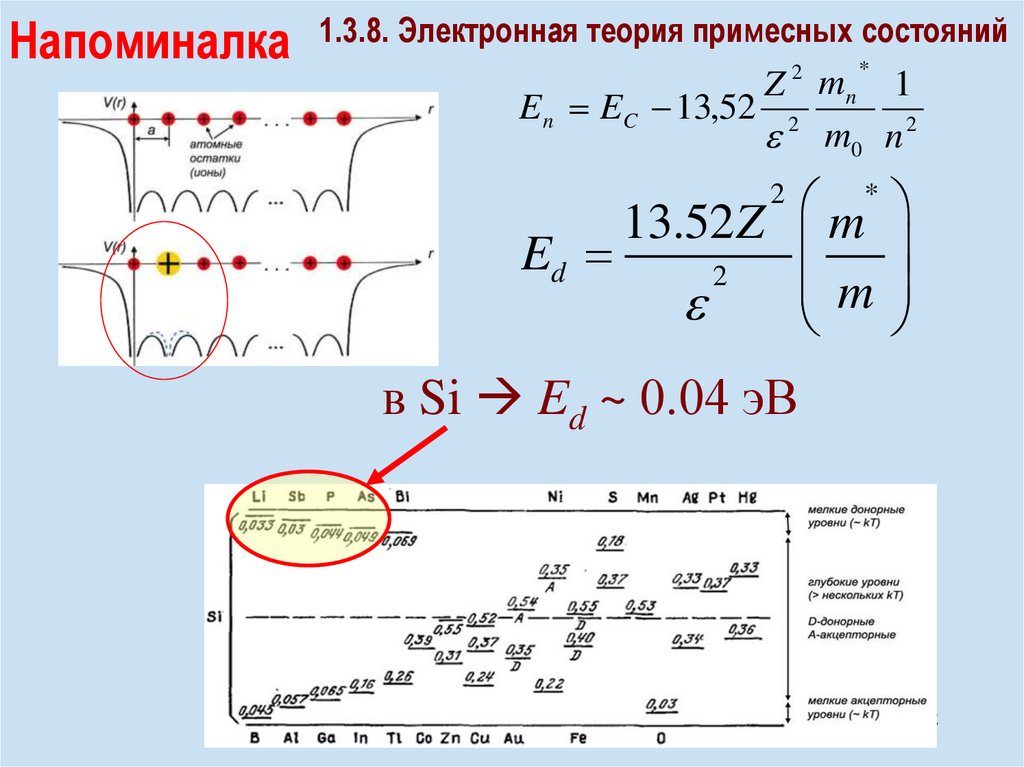

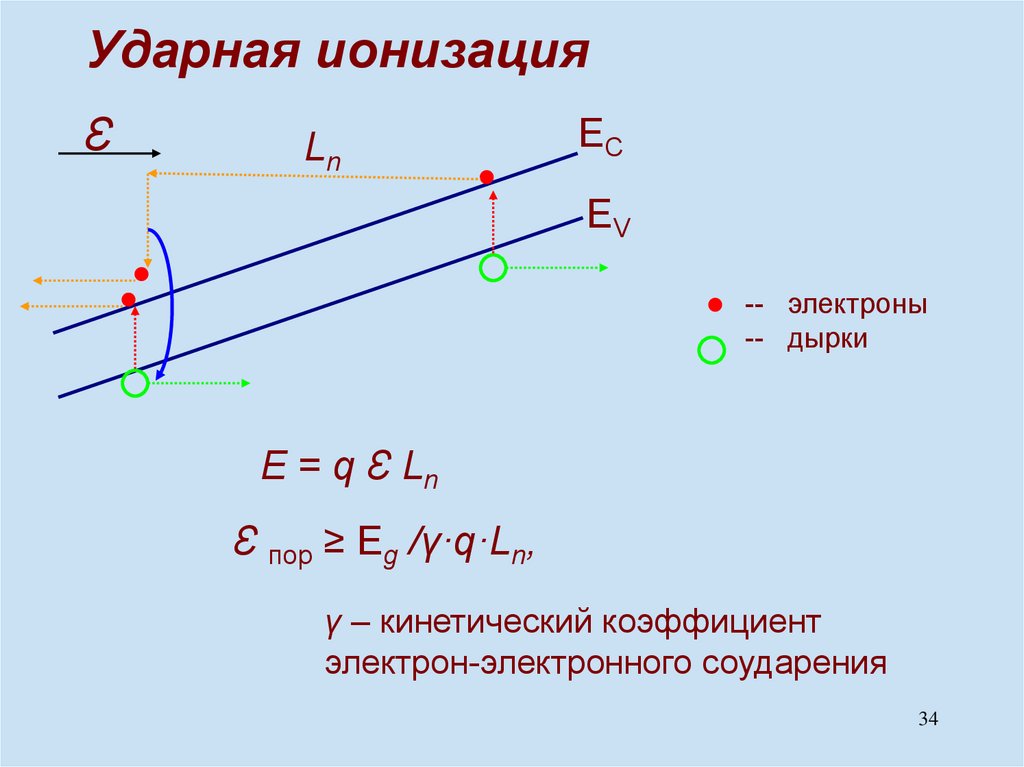

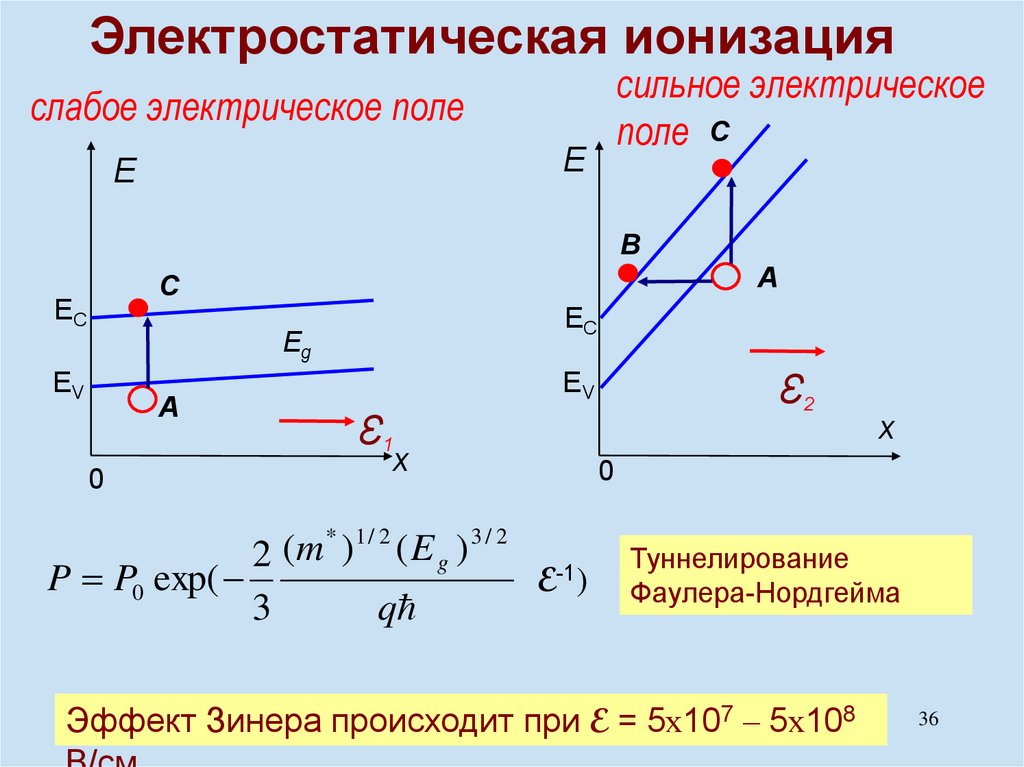
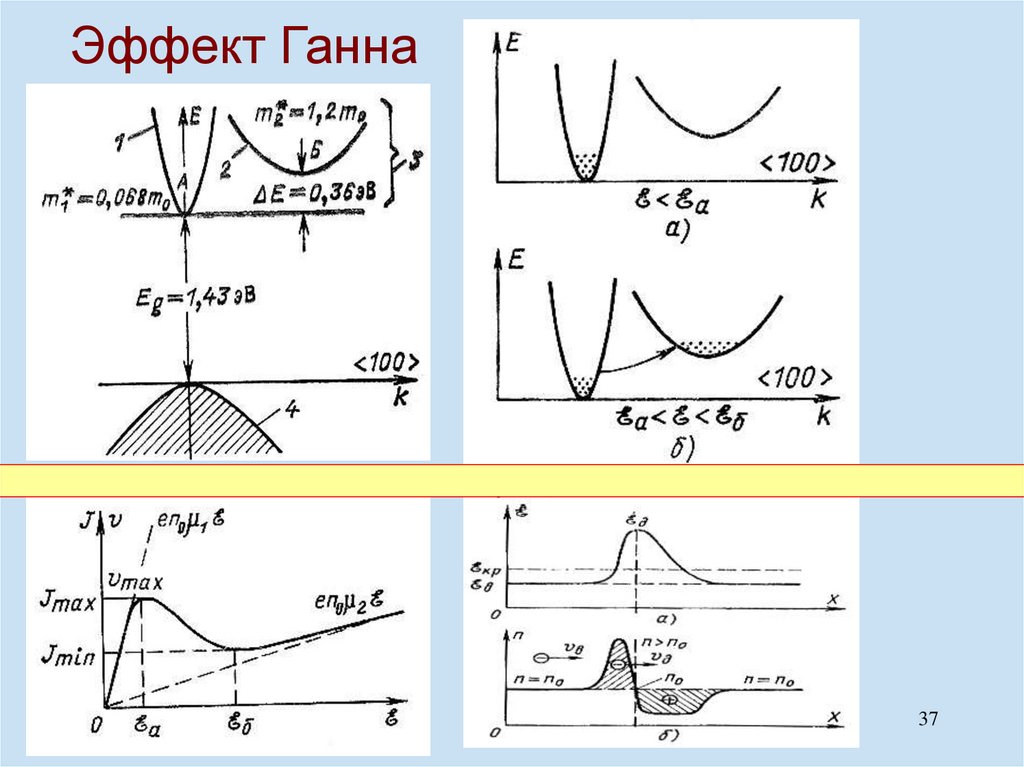


 physics
physics








