Similar presentations:
Пирамида. Виды правильных пирамид (тема 20)
1.
2.
Тема 20.Пирамида.
3.
План лекции1. Понятие пирамиды.
2. Правильная пирамида.
3. Виды правильных пирамид.
4. Развёртка пирамиды.
5. Площадь и объем.
4.
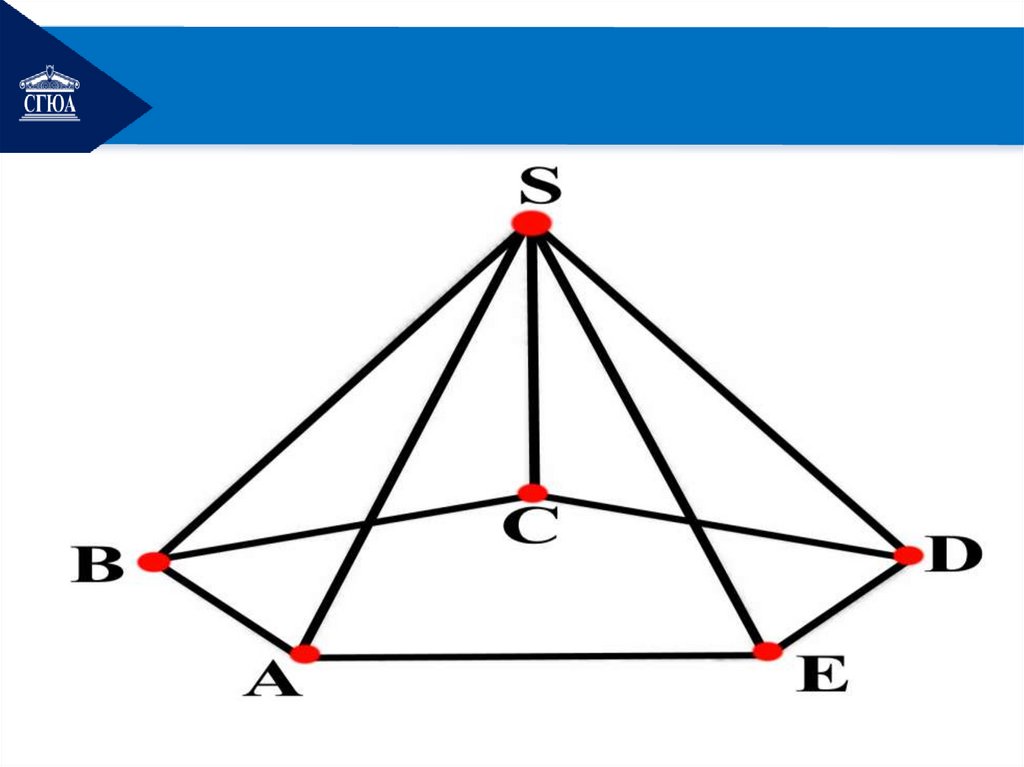
1. Понятие пирамидыОпр. Пирамидой называется
многогранник, в основании
которого лежит
многоугольник, а остальные
грани – треугольники,
имеющие общую вершину,
называемую вершиной
пирамиды.
5.
6.
7.
•Общая вершина боковыхграней называется вершиной
пирамиды.
•Отрезки, соединяющие
вершину пирамиды с
вершинами основания,
называются рёбрами
пирамиды.
8.
• Боковые треугольникназываются гранями
пирамиды.
•Перпендикуляр, проведенный
из вершины пирамиды к
плоскости основания,
называется высотой
пирамиды.
9.
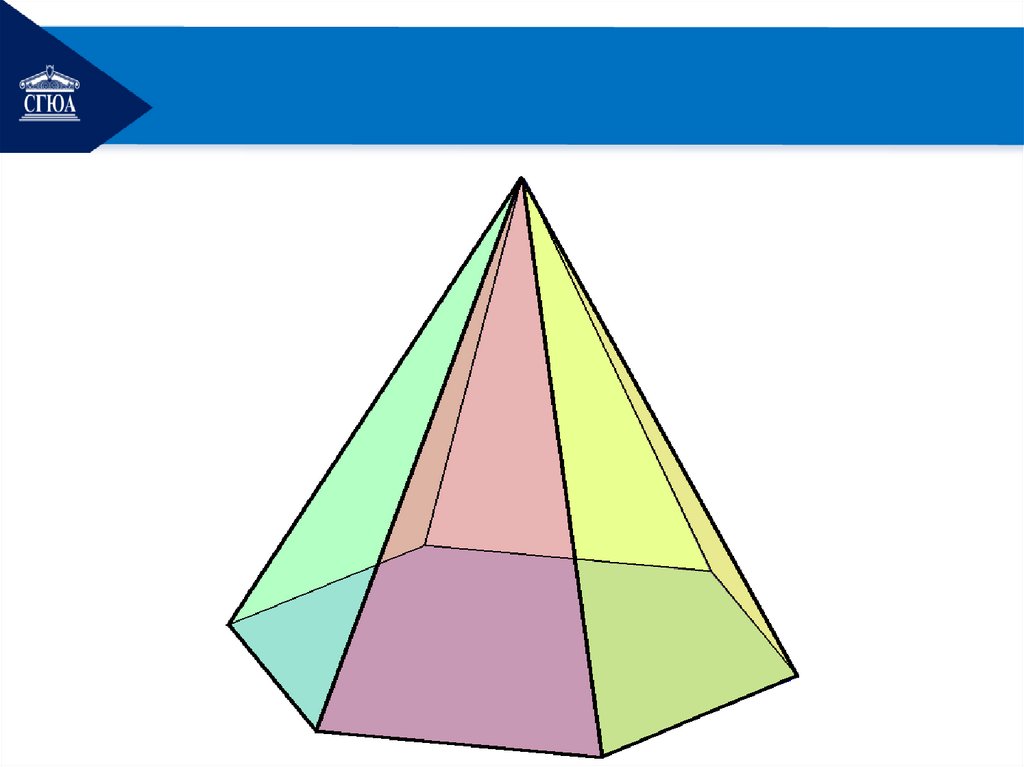
2. Правильная пирамидаОпр. Пирамида, основанием
которой является правильный
многоугольник, а вершина
проектируется в центр
основания,
называется правильной
пирамидой.
10.
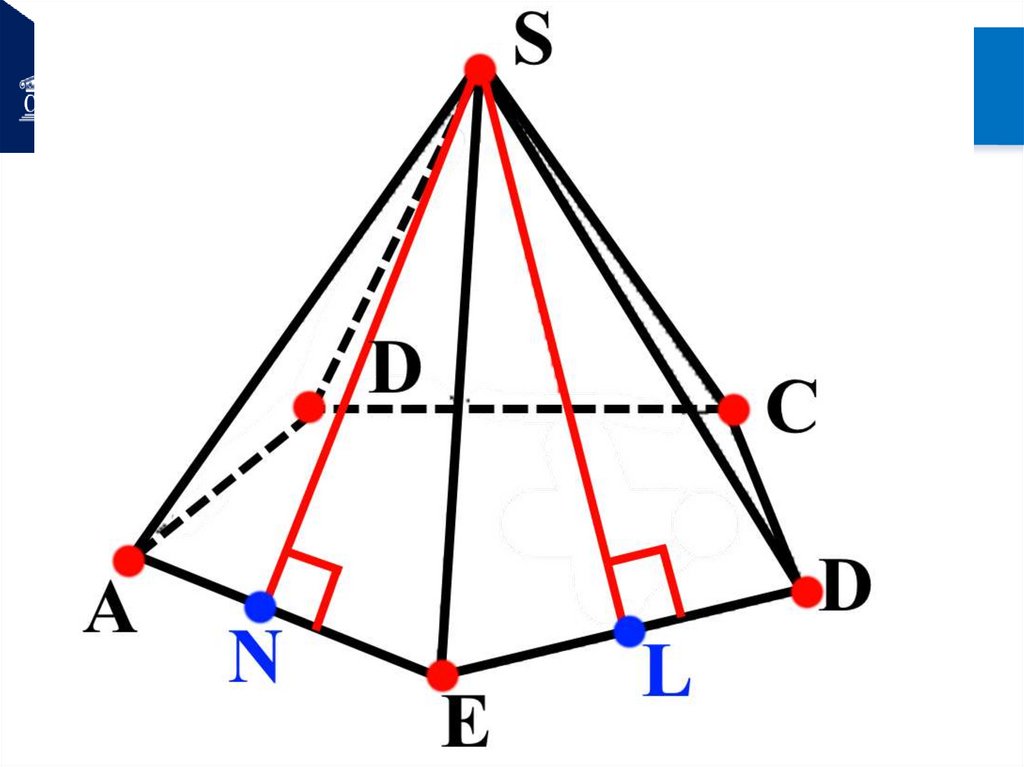
Боковые грани правильнойпирамиды — равные
равнобедренные
треугольники.
Высота боковой грани
правильной пирамиды
называется апофемой.
11.
12.
Свойства правильнойпирамиды
•боковые ребра равны;
•боковые грани равны (все
равнобедренные
треугольники);
•апофемы равны;
13.
• боковые ребра одинаковонаклонены к плоскости
основания;
•основание высоты пирамиды
является центром вписанной и
описанной около основания
окружностей;
•высота образует с апофемами
равные углы.
14.
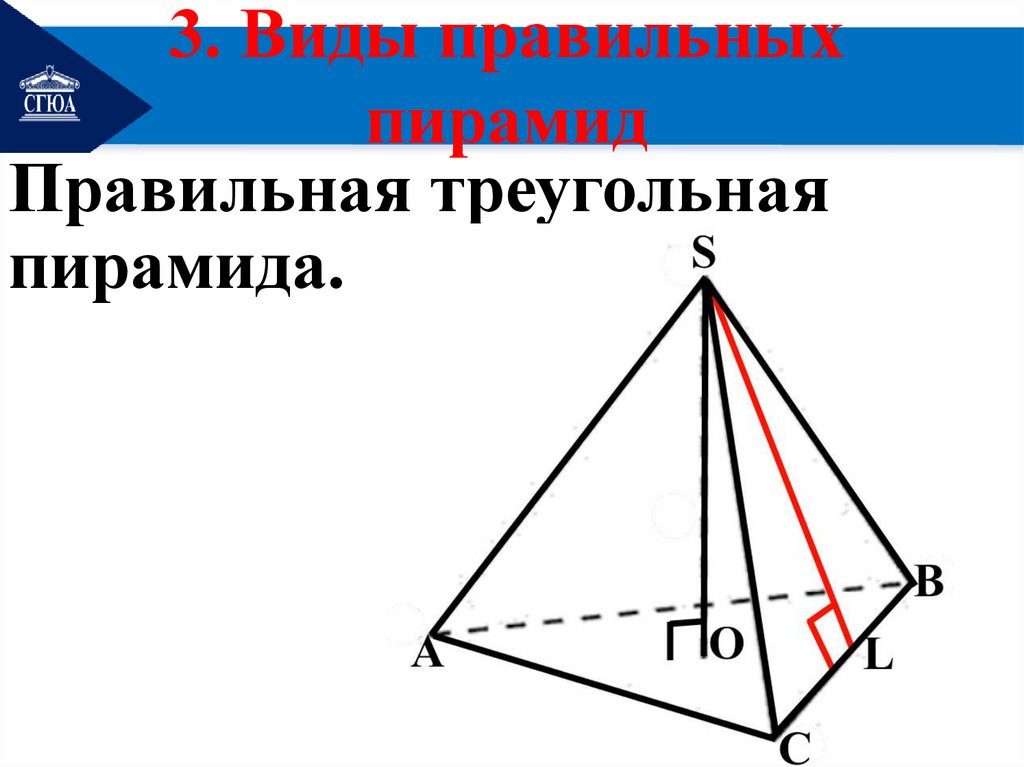
3. Виды правильныхпирамид
Правильная треугольная
пирамида.
15.
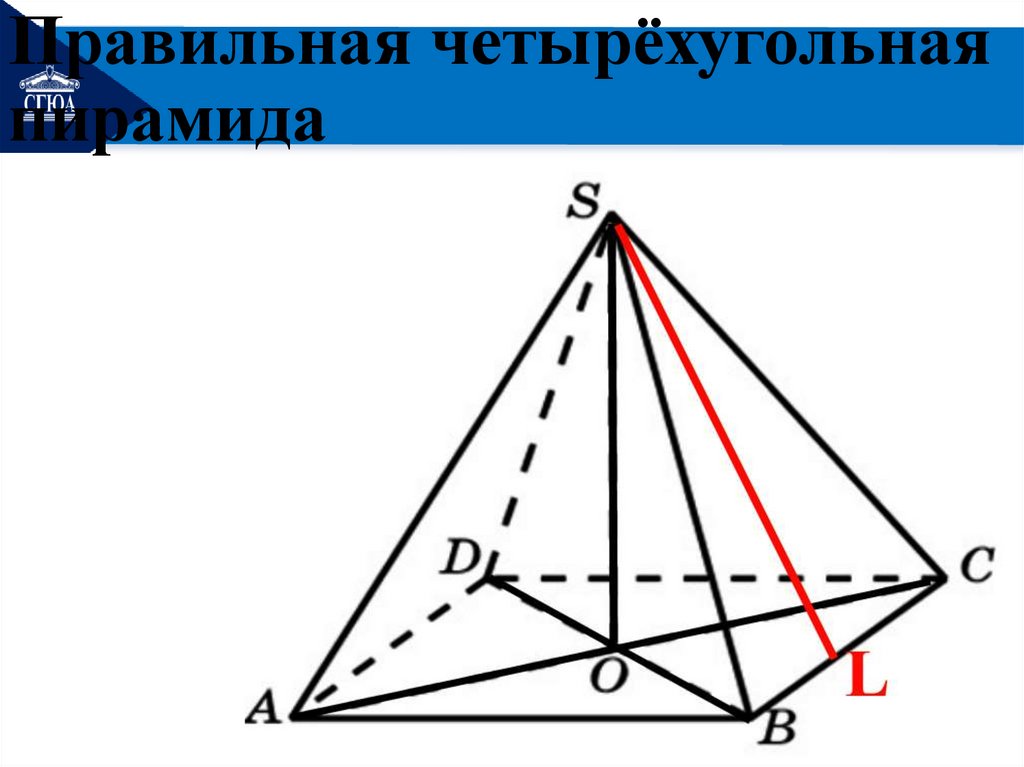
Правильная четырёхугольнаяпирамида
16.
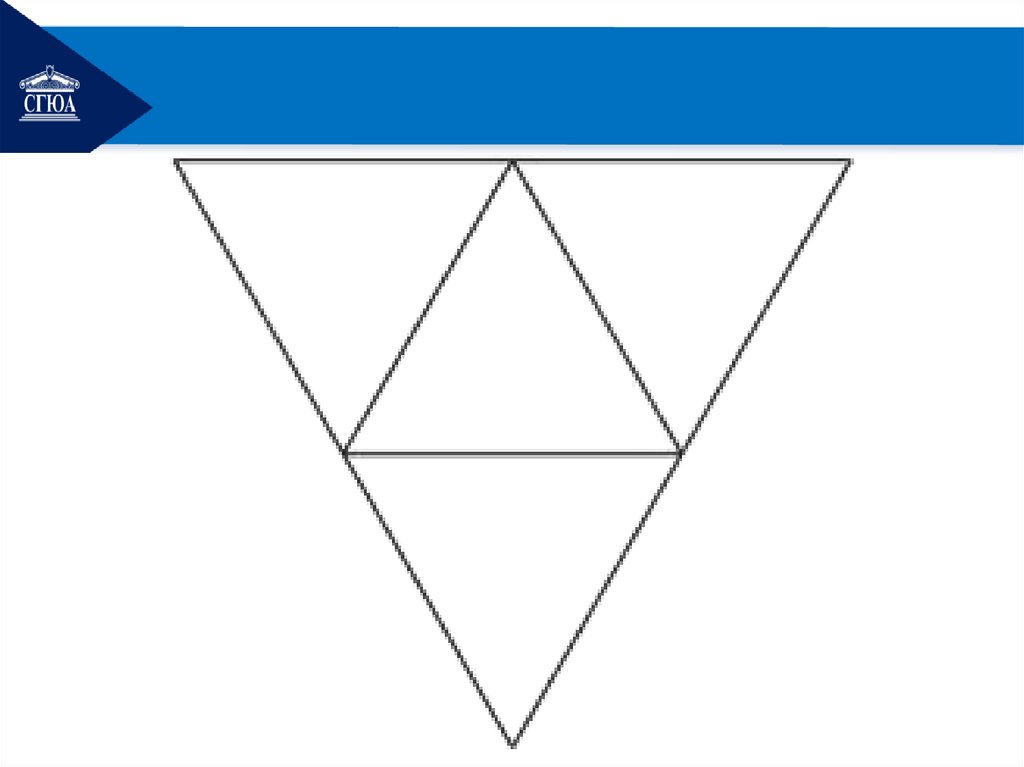
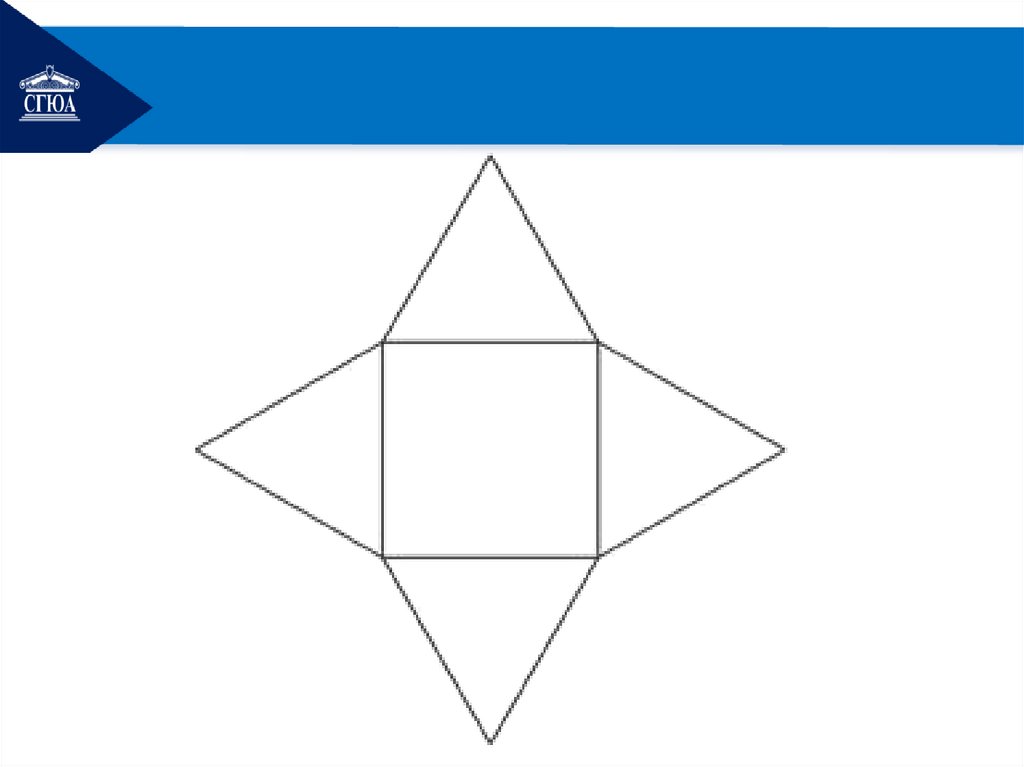
4. Развёртка пирамидыОпр. Развёрткой называется
плоская фигура, полученная
при совмещении поверхности
геометрического тела с одной
плоскостью (без наложения
граней или иных элементов
поверхности друг на друга).
17.
Если отсек поверхности можетбыть совмещён с плоскостью
без разрывов и склеивания, то
такую поверхность называют
развёртывающейся, а
полученную плоскую фигуру —
её развёрткой.
18.
19.
20.
5. Площадь и объёмТеорема(Площадь боковой
поверхности)
Площадь боковой поверхности
пирамиды равна половине
произведения периметра
основания на апофему:
21.
1S бок Pосн Lапоф
2
22.
Теорема(Площадь полнойповерхности)
Площадь полной поверхности
пирамиды равна сумме
площадей боковой
поверхности и основания:
S полн Sбок Sосн
23.
Теорема(Объём пирамиды)Объём пирамиды равен одной
трети произведения площади
основания на высоту:
1
V S осн h
3
24.
5. Связка элементов пирамидыСвязка – это три элемента
пирамиды образующие
прямоугольный треугольник.
Связка 1. Содержит высоту,
радиус описанной окружности,
боковое ребро.
25.
Пусть боковое ребро –b,высота – h, R – радиус
описанной окружности:
b h R
2
2
2
26.
Связка 2. Содержит высоту,радиус вписанной окружности,
апофему:
Пусть апофема –L, высота – h,
r – радиус вписанной
окружности:
L h r
2
2
2
27.
Связка 3. Содержит апофему,боковое ребро, половину
стороны.
Пусть боковое ребро –b, L –
апофема, a/2 – половина
стороны:
2
a
2
2
b
L
4
28.
Связка 4. Содержит радиусвписанной окружности,
половину стороны, половину
диагонали основания.
Пусть r – радиус вписанной
окружности, a/2 – половина
стороны, d/2 – половина
диагонали:
29.
22
d
a
2
r
4
4













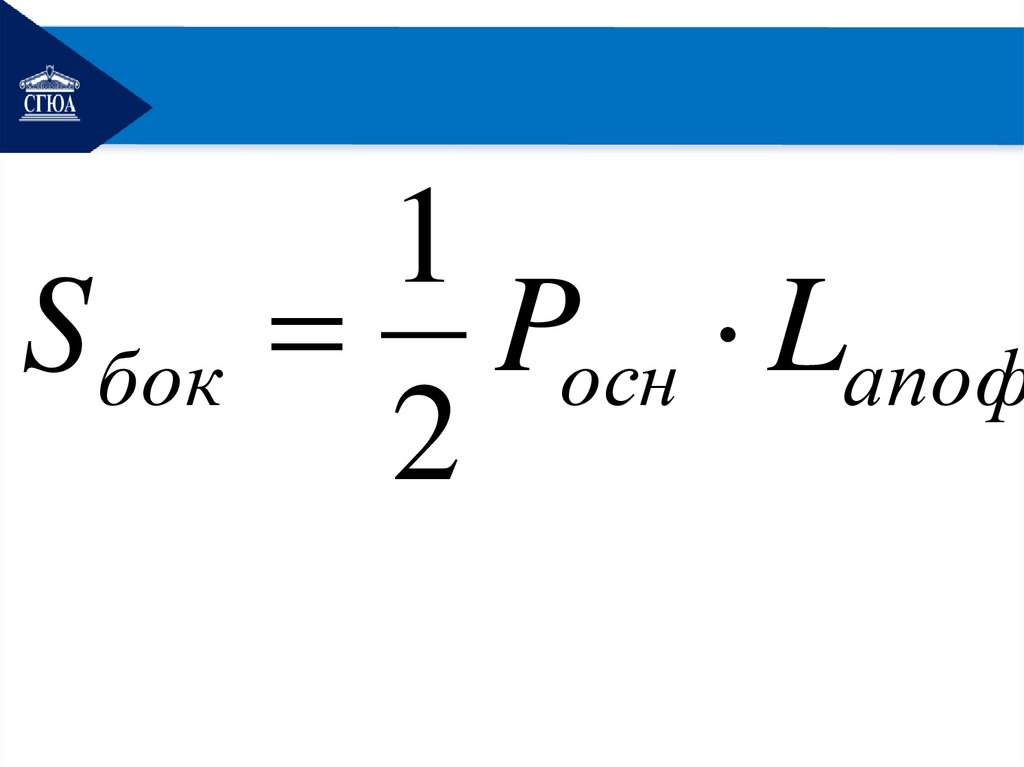







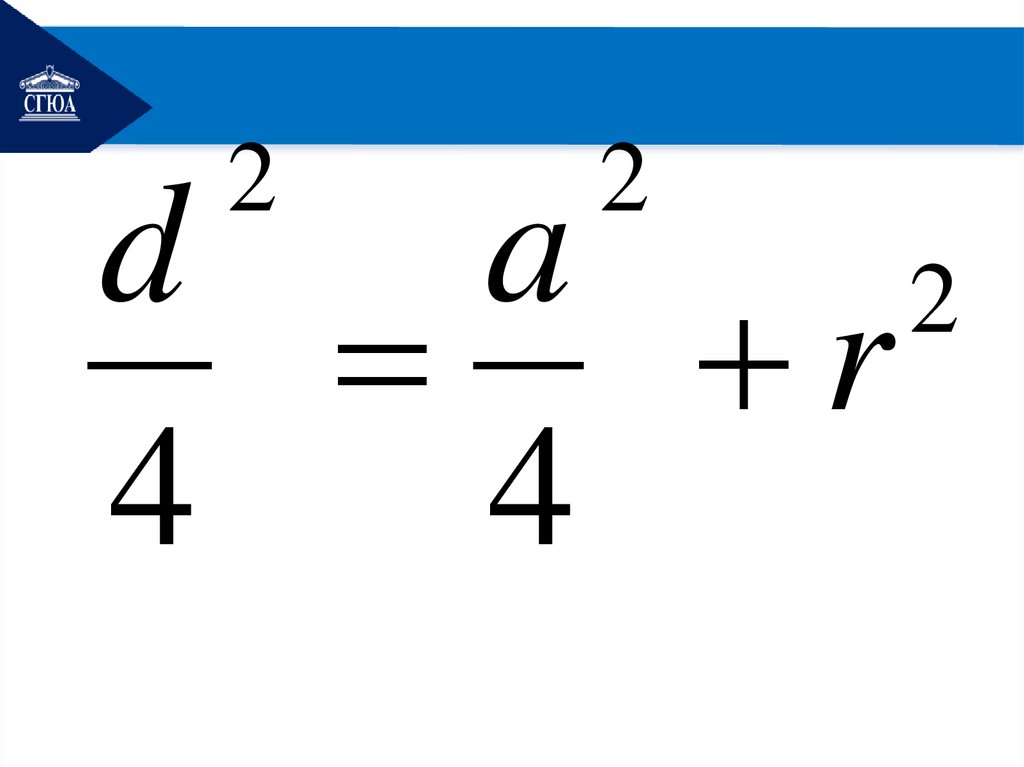

 mathematics
mathematics








