Построение уравнения регрессии. Урок № 37

1. Построение уравнения регрессии

Урок № 37

2. Основные вопросы темы:

Статистические методы выявления
взаимосвязей
Исследование корреляционных связей
Построение уравнения регрессии

3. Дидактическая цель

Применение полученных знаний, умений и
навыков в процессе выполнении
самостоятельной вычислительной работы.
Знать:
– статистические методы выявления
взаимосвязей;
Иметь представление:
– об исследовании наличия корреляционной
связи

4. Статистика

Статистика – это наука, которая
позволяет увидеть закономерности в хаосе
случайных данных, выделить в них
устойчивые связи и определить наши
действия с тем, чтобы увеличить долю
правильно принятых решений.

5. Статистика

Как
и
все
математические
науки,
статистика появилась из потребностей
сократить
случайные
данные
до
минимума. Но сделать это полностью
редко
когда
удается.
Применяя
статистические методы, мы стремимся
найти закономерности в случайных данных
и
воспользоваться
найденными
закономерностями.

6. Виды признаков

Все процессы и явления, окружающие нас,
взаимосвязаны друг с другом.
При изучении конкретных связей одни
признаки выступают в роли факторов,
другие в роли результатов.

7. Виды признаков

• Так, например, уровень производительности
труда работников предприятия будет
зависеть от совершенства применяемого
оборудования, степени совершенства
технологии, организации производства труда
и управления и других самых различных
факторов.

8. Виды признаков

Факторный признак – это признак, на
который
можно
оказать
какое-либо
воздействие, управлять им.
Результативный признак – это
признак, который является результатом
влияния этих факторов.

9. Виды признаков

При изучении зависимости между
производительностью труда рабочих и
энерговооруженностью их труда уровень
производительности труда является
результативным признаком, а
энерговооруженность труда рабочих —
факторным признаком, которым мы можем
управлять.
Например, можно повысить
энерговооруженность и воздействовать тем
самым на производительность труда, если
такая связь существует.

10. Статистические методы

• С помощью статистических методов
изучения зависимостей можно установить,
как проявляется теоретически возможная
связь в данных конкретных условиях.
• Статистика не только отвечает на вопрос о
реальном существовании намеченной
теоретическим анализом связи, но дает
количественную характеристику этой
зависимости.

11. Статистические методы

Зная характер зависимости одного явления
от других
• можно объяснить причины и размер
изменений в явлении,
• планировать необходимые мероприятия
для дальнейшего его изменения.

12. Линейная зависимость

Простейшей формой зависимости между
переменными является линейная
зависимость.
Проверка ее параметров является одним
из важнейших направлений в приложениях
математической статистики.

13. Вопросы о линейной зависимости

Существуют два вопроса о линейной
зависимости:
1. Связаны ли между собой линейно
переменные X и Y ?
2. Какова формула связи переменных
и Y?
X

14. Вопросы о линейной зависимости

• В первом случае переменные X и Y
выступают как равноправные, здесь нет
независимой и зависимой переменных.
• Во втором случае речь может идти о
нахождении зависимости одной переменной
от другой.

15. Вопросы о линейной зависимости

• Например, оценивание формулы
ŷ(х) = а0 + а1х
(где a0 и а1 — неизвестные коэффициенты
такой зависимости).
В этом случае
переменная X является независимой
(объясняющей),
переменная Y— зависимой (объясняемой).

16. Вопросы о линейной зависимости

• Вопрос о нахождении формулы зависимости
можно ставить после положительного ответа на
вопрос о существовании такой зависимости, но
эти два вопроса можно решать и одновременно.
• Для ответа на поставленные вопросы
существуют специальные статистические
методы и, соответственно, показатели,
значения которых свидетельствуют о наличии
или отсутствии линейной связи между
переменными.

17. Вопросы о линейной зависимости

• В первом случае это коэффициент
корреляции величин X и Y.
• Во втором случае — коэффициенты
линейной регрессии а0 и а1, их
стандартные ошибки и t-статистики,
по значениям которых проверяется гипотеза
об отсутствии связи величин Х и Y.

18. Исследование корреляционных связей

Корреляционная связь анализирует
зависимость среднего значения
результативного признака y от изменения
факторного признака x.

19. Исследование корреляционных зависимостей

Исследование корреляционных зависимостей
включает в себя ряд этапов:
1) Предварительный анализ свойств
совокупности;
2) Установление факта наличия связи,
определение ее направления и формы;
3) Измерение степени тесноты связи между
признаками;
4) Оценка связи, полученной по выборочным
данным для всей генеральной совокупности.

20. Методы оценки

Для оценки корреляционной связи между
признаками, заданными рядом наблюдений,
существуют различные методы.
По направлению различают прямую и
обратную связь.
Чтобы определить связь, иногда используют
предварительный анализ: параллельное
сравнение данных, графический метод
(построение поля корреляции).

21. Поле корреляции

Полем корреляции называется
совокупность точек результативного и
факторного признаков.

22. Построение поля корреляции

Для построения поля корреляции по оси
абсцисс откладываются значения
факторного признака, а по оси ординат –
соответствующие значения
результативного.
На их пересечении ставится точка.
Множество точек и образует поле
корреляции.
По нему можно судить о величине
разброса значений и о наличии связи.

23. Критерии оценки

Для более точной числовой оценки наличия
и тесноты связи между признаками
используют различные критерии:
коэффициент Фехнера,
критерий Пирсона,
коэффициент корреляции.
Наиболее точный вывод о наличии или
отсутствии корреляционной связи дает
линейный коэффициент корреляции.

24. Линейный коэффициент корреляции

n
r
( x x)( y y)
i 1
i
i
n x y
Где n – объем выборки
x i, y i - выборочные значения соответствующих
признаков;
x ср, y ср - среднее арифметическое выборочных значений
соответствующих признаков;
σx, σy - средние квадратические отклонения выборочных
значений.

25. Корреляционная связь

Коэффициент корреляции принимает значения
в интервале [-1;1].
Близость расчетного коэффициента к - 1
свидетельствует о наличии тесной обратной
связи между исследуемыми признаками.
Коэффициент корреляции, приближающийся
к +1, свидетельствует о прямой зависимости.
Незначительное отклонение коэффициента
корреляции от нуля означает отсутствие связи.

26. Корреляционная связь

Коэффициент корреляции оценивают с помощью
критерия Стьюдента, проверка которого
осуществляется по следующему алгоритму:
1) Выдвигается гипотеза: «Между переменными не
существует линейной связи».
2) Альтернативная гипотеза: между переменными х и у
существует некая линейная связь
Для оценки этих двух гипотез используем критерий
Стьюдента:
t расч.
r n 2
1 r
2

27. Корреляционная связь

Расчетное значение критерия сравниваем с
табличным значением t-распределения
Стьюдента для уровня значимости α = 1 - γ.
Если t-распределения больше t-табличного, то с
вероятностью γ = 1 - α можно утверждать что
между переменными существует некая связь
Если t-распределения меньше или равно tтабличному то с вероятностью γ можно
утверждать что между переменными не
существует линейной связи.

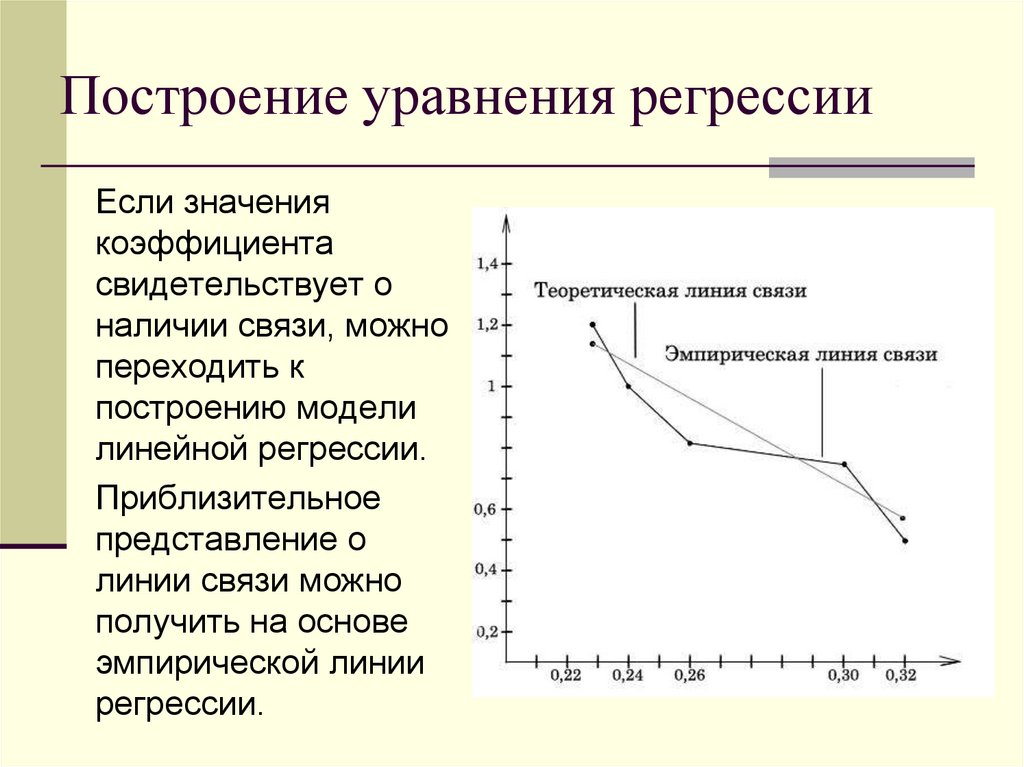
28. Построение уравнения регрессии

Если значения
коэффициента
свидетельствует о
наличии связи, можно
переходить к
построению модели
линейной регрессии.
Приблизительное
представление о
линии связи можно
получить на основе
эмпирической линии
регрессии.

29. Построение уравнения регрессии

Метод наименьших квадратов
используется для нахождения такой функции,
которая наилучшим образом соответствует
.
эмпирическим
данным, т. е. сумма квадратов
отклонений эмпирических точек от
теоретической линии регрессии минимальна.
Теоретическая линия регрессии может быть
представлена прямой:
ŷ(х) = а0 + а1х

30. Построение уравнения регрессии

Для определения коэффициентов линейной
регрессии используются следующие
формулы:
y
a1 r
x
a y a x
1
0

31. Построение уравнения регрессии

Решив систему уравнений, получаем
значения а0 и а1, которые подставляются в
уравнение линейной регрессии:
ŷ(х) = а0 + а1х
Параметр а1 в уравнении называют
коэффициентом регрессии, который показывает
на сколько в среднем изменится величина
результативного признака у при изменении
факторного признака х на единицу.

32. Построение уравнения регрессии

Произведенные вычисления позволяют
производить вычисление коэффициента
корреляции и параметров уравнения
регрессии одновременно.

33. Основные вопросы темы

Дать понятие факторного признака.
Что такое результативный признак?.
Что называется полем корреляции?
Как оценить коэффициент корреляции?
С помощью какого критерия оценивают
коэффициент корреляции?

34. Домашнее задание

Литература
Калинина В. Н.
Глава 12.
Корреляционно-регрессионный анализ.