Similar presentations:
Векторы. Понятие вектора
1. Векторы
Выполнила ученица 9 классаКудрявцева Таисия
Учитель: Журкова В.П.
2. Содержание:
Понятие вектора
Коллинеарные векторы
Равенство векторов
Сумма двух векторов
Законы сложения. Правило параллелограмма
Сумма нескольких векторов
3. Понятие вектора
• Определение.Отрезок, для которого указано,
какой из его концов считается
началом, а какой - концом,
называется вект ором.
4. Понятие вектора
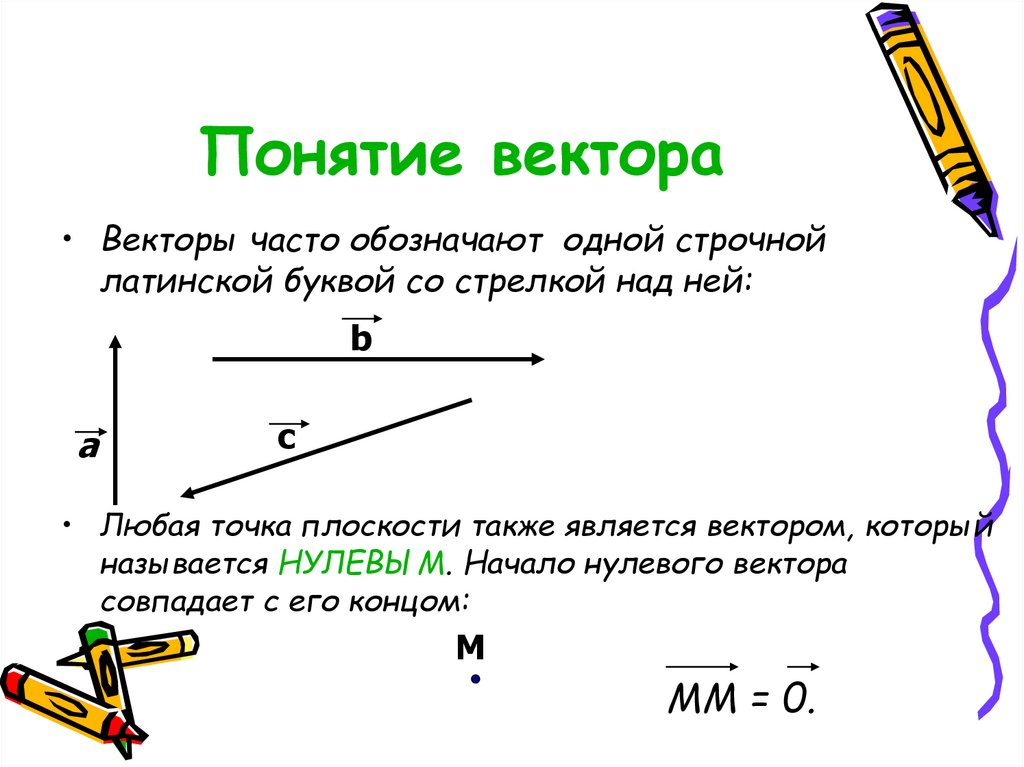
• Векторы часто обозначают одной строчнойлатинской буквой со стрелкой над ней:
b
a
c
• Любая точка плоскости также является вектором, который
называется НУЛЕВЫМ. Начало нулевого вектора
совпадает с его концом:
М
ММ = 0.
5. Понятие вектора
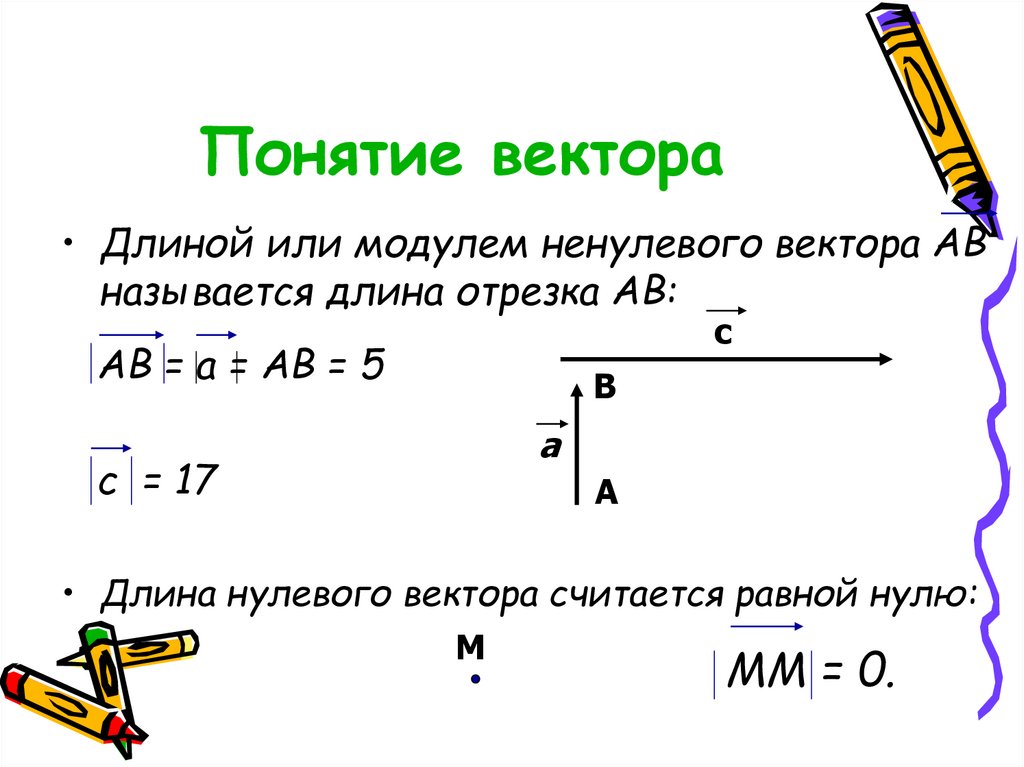
• Длиной или модулем ненулевого вектора АВназывается длина отрезка АВ:
с
АВ = а = АВ = 5
В
a
с = 17
А
• Длина нулевого вектора считается равной нулю:
М
ММ = 0.
6. Коллинеарные векторы
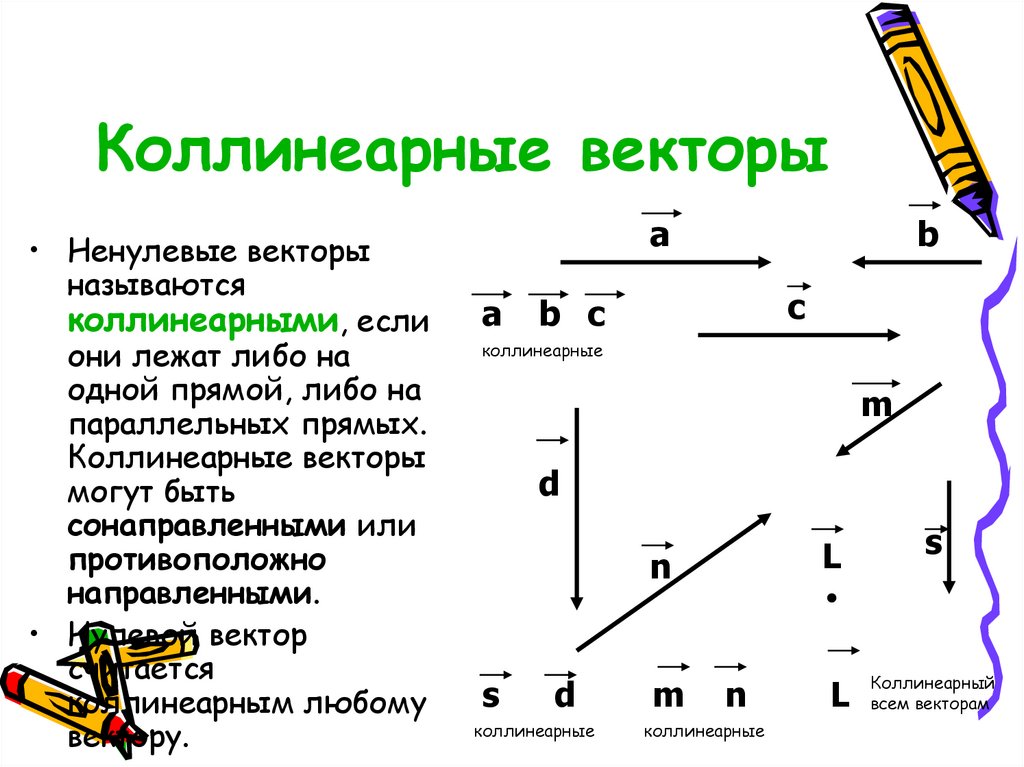
• Ненулевые векторыназываются
коллинеарными, если
они лежат либо на
одной прямой, либо на
параллельных прямых.
Коллинеарные векторы
могут быть
сонаправленными или
противоположно
направленными.
• Нулевой вектор
считается
коллинеарным любому
вектору.
а
а
b
c
b c
коллинеарные
m
d
L
n
s
d
коллинеарные
m
n
коллинеарные
L
s
Коллинеарный
всем векторам
7. Равенство векторов
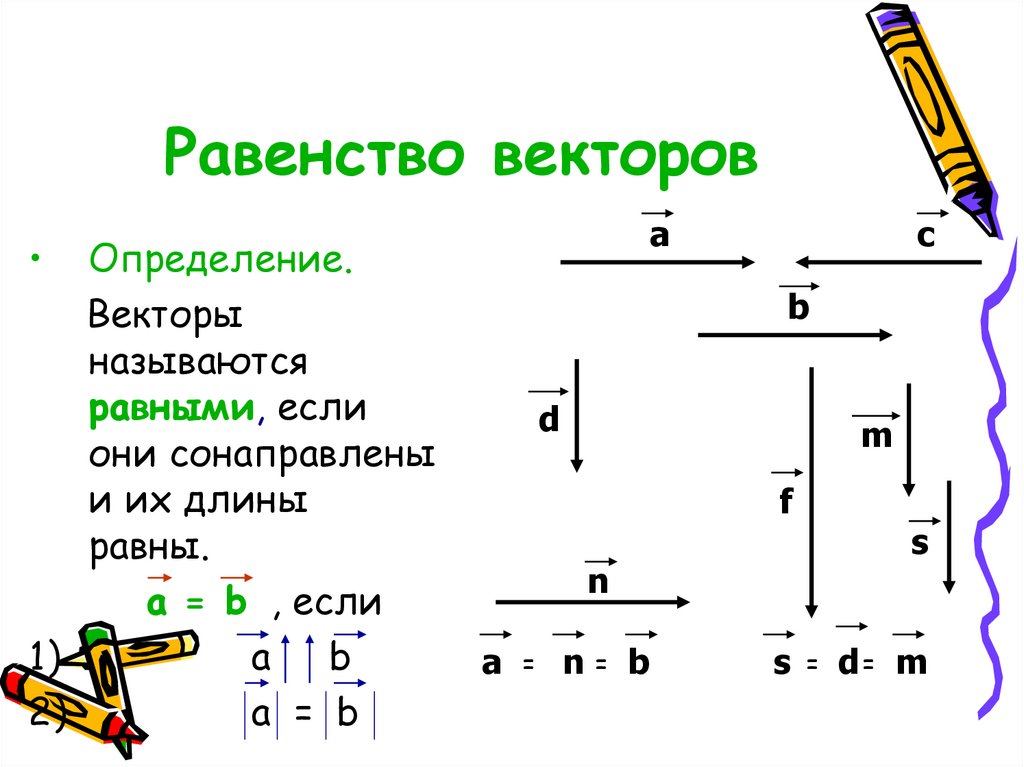
Определение.Векторы
называются
равными, если
они сонаправлены
и их длины
равны.
а = b , если
1)
а
b
2)
а = b
а
c
b
d
m
f
s
n
а
=
n
=
b
s
=
d= m
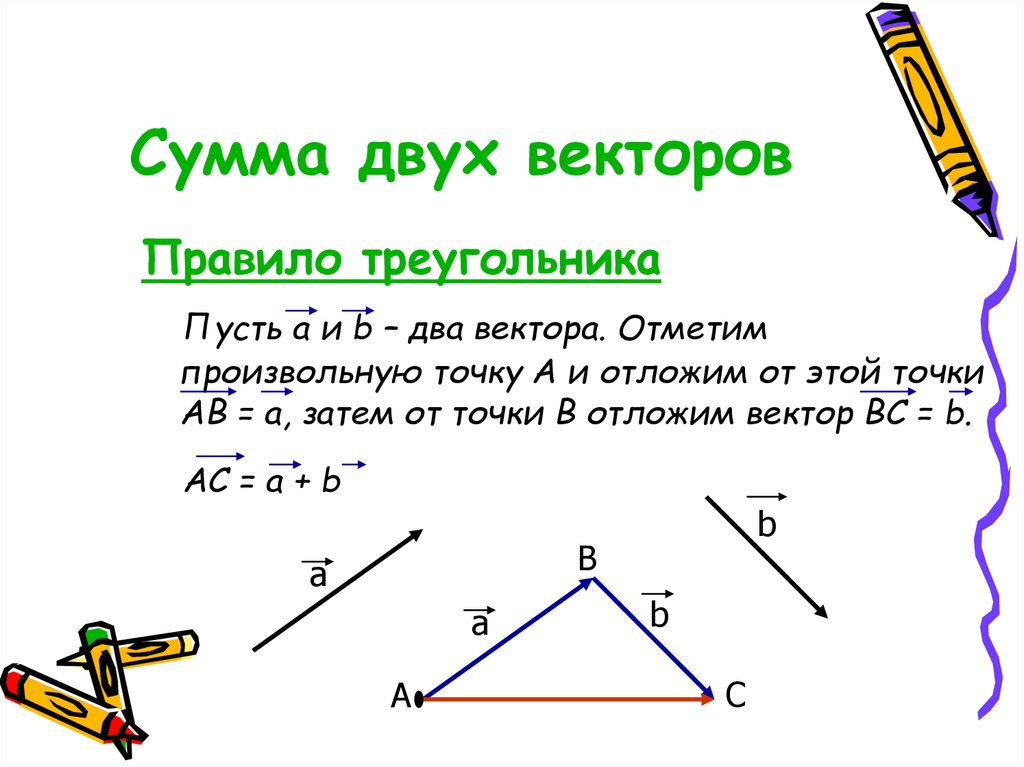
8. Сумма двух векторов
Правило треугольникаПусть а и b – два вектора. Отметим
произвольную точку А и отложим от этой точки
АВ = а, затем от точки В отложим вектор ВС = b.
АС = а + b
b
B
a
a
A
b
C
9. Законы сложения векторов
1) а+b=b+a(переместительный закон)
Правило параллелограмма
Пусть а и b – два вектора. Отметим
произвольную точку А и отложим от этой
точки АВ = а, затем вектор АD = b. На этих
векторах построим параллелограмм АВСD.
АС = АВ + BС = а+b
a
D
C
АС = АD + DС = b+a
b
a
b
b
2) (а+b)+c=a+(b+c)
(сочетательный закон)
A
a
B
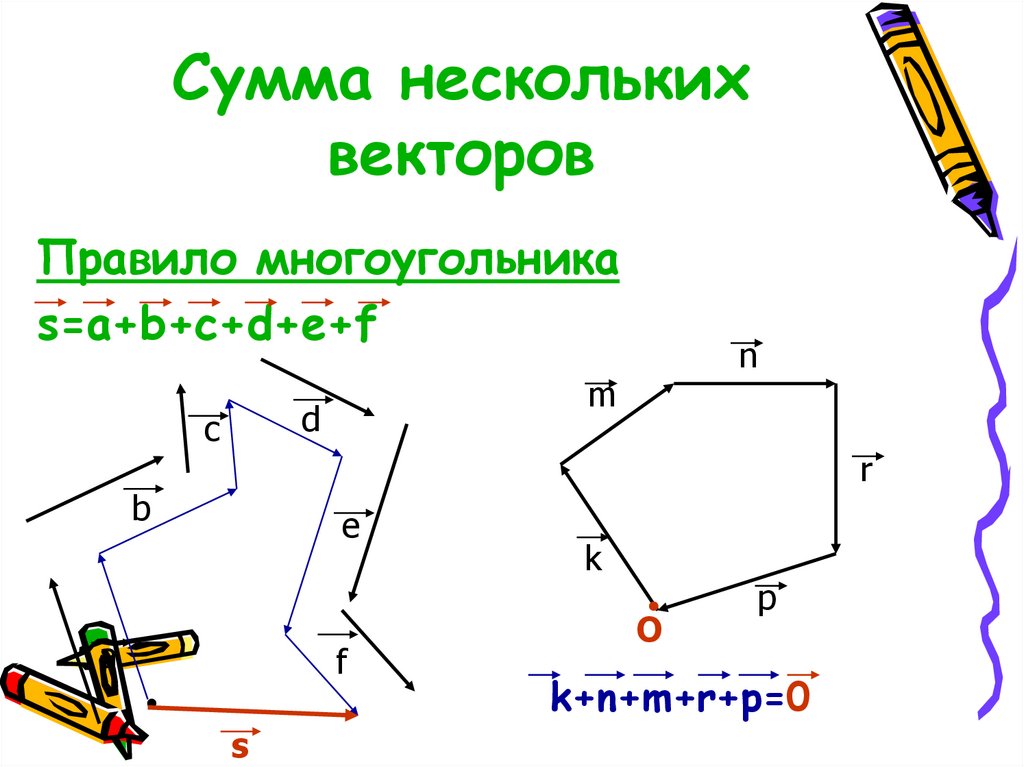
10. Сумма нескольких векторов
Правило многоугольникаs=a+b+c+d+e+f
m
d
c
n
r
b
e
a
f
s
k
O
p
k+n+m+r+p=0





 mathematics
mathematics








