Векторы. Понятие вектора

1. Понятие вектора

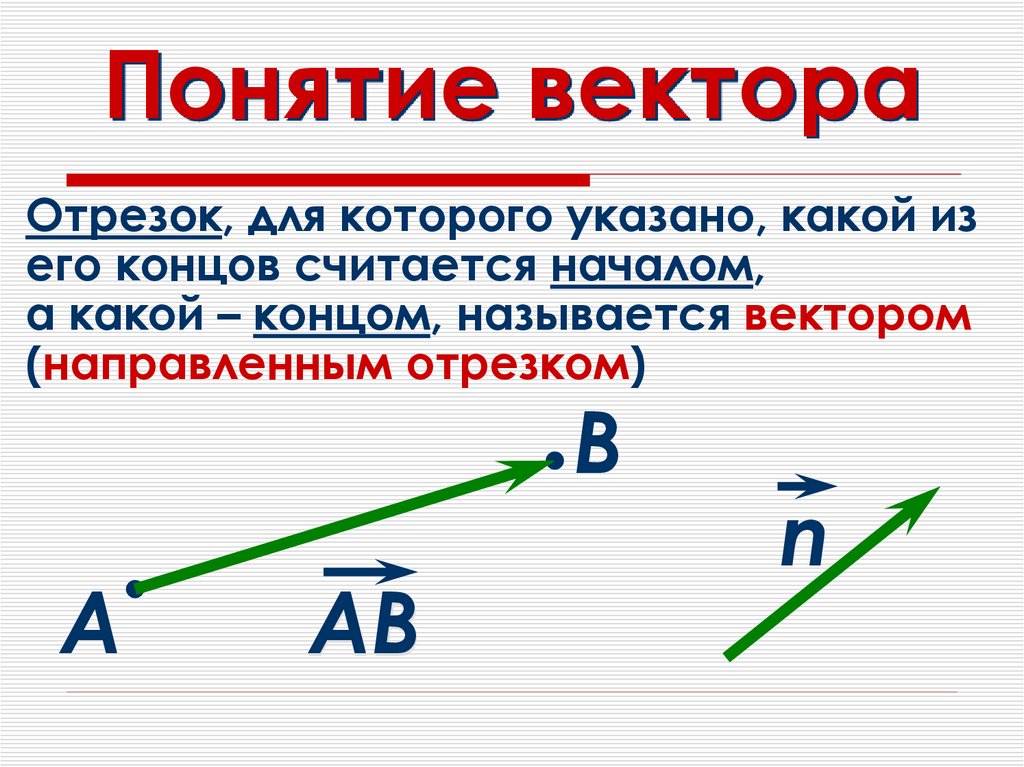
Отрезок, для которого указано, какой из
его концов считается началом,
а какой – концом, называется вектором
(направленным отрезком)
В
А
АВ
n

2. Назвать все изображенные векторы

3. Нулевой вектор

Любая точка на плоскости может
рассматриваться как вектор.
Такой вектор называется нулевым(
нуль- вектором).
М
ММ = 0

4. Длина вектора

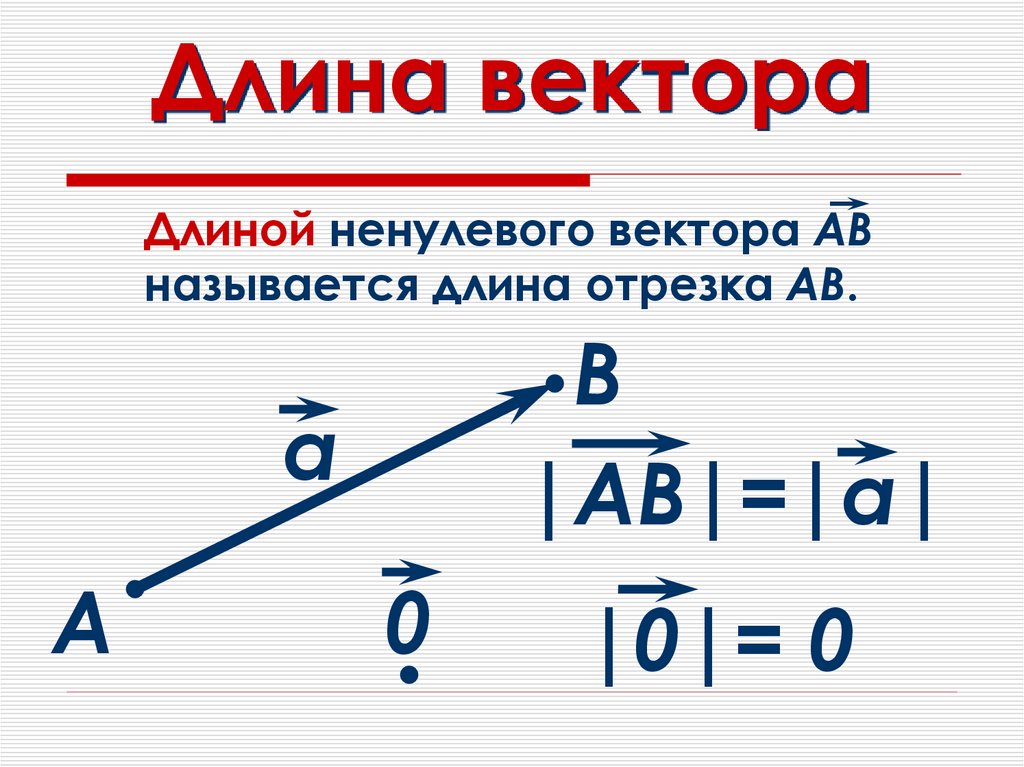
Длиной ненулевого вектора АВ
называется длина отрезка АВ.
В
|АВ|=|а|
а
А
0
|0|= 0

5. Коллинеарность векторов

Ненулевые векторы называются
коллинеарными, если они лежат на одной
прямой или на параллельных прямых.
q
р
r

6. Коллинеарность векторов

- Нулевой вектор коллинеарен
любому вектору
- Обозначение коллинеарных
векторов:
а║b

7. Сонаправленные векторы

Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.
q
р
q↑↑р

8. Противоположно направленные векторы

Два коллинеарных вектора называются
противоположно направленными, если
они не сонаправлены.
а
b
a↑↓b

9. Равные векторы

Ненулевые векторы называются
равными, если они сонаправлены и
их длины равны.
q
р
q↑↑р
|q|=|р|
q=р

10. Свойства ненулевых коллинеарных векторов

Если а b, b с,
то а с
…
…

11. Откладывание вектора от данной точки

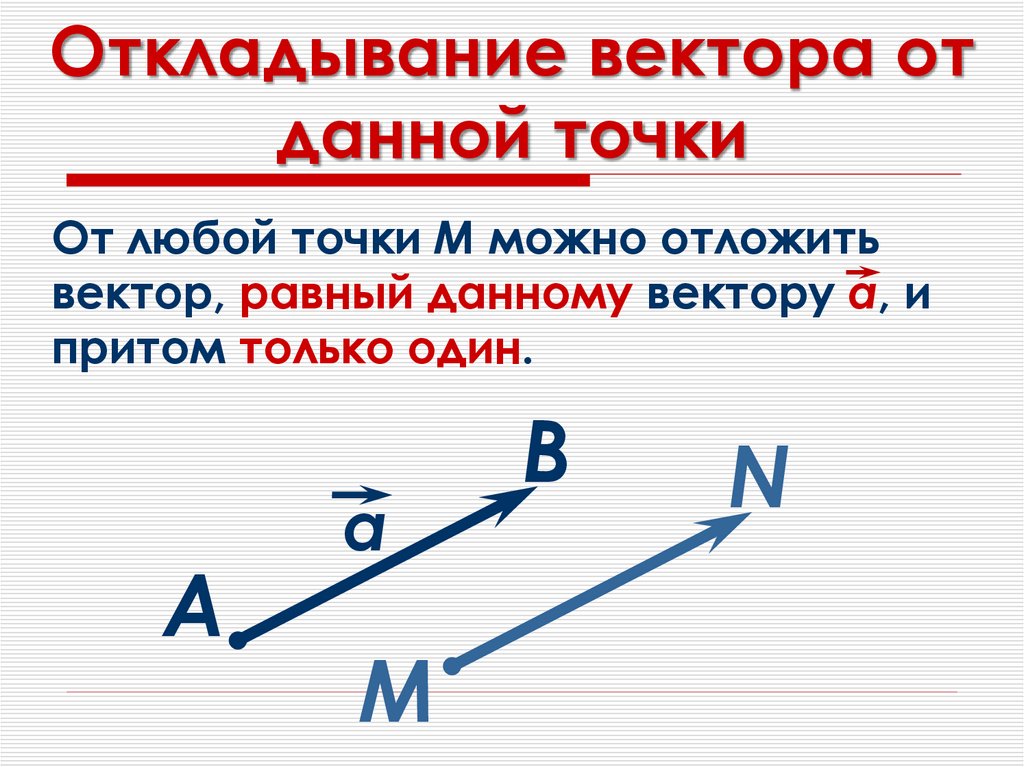
От любой точки М можно отложить
вектор, равный данному вектору а, и
притом только один.
А
a
М
В
N

12.

Действия
с векторами

13. Действия над векторами

1. Сложение векторов( векторная
форма, координатная форма)
2. Вычитание векторов
3. Умножение вектора на число

14. Сложение векторов в векторной форме

1. Правило треугольника
2. Правило параллелограмма
Результатом сложения и
вычитания векторов является
вектор

15. Сложение векторов

q
O
q
р
р
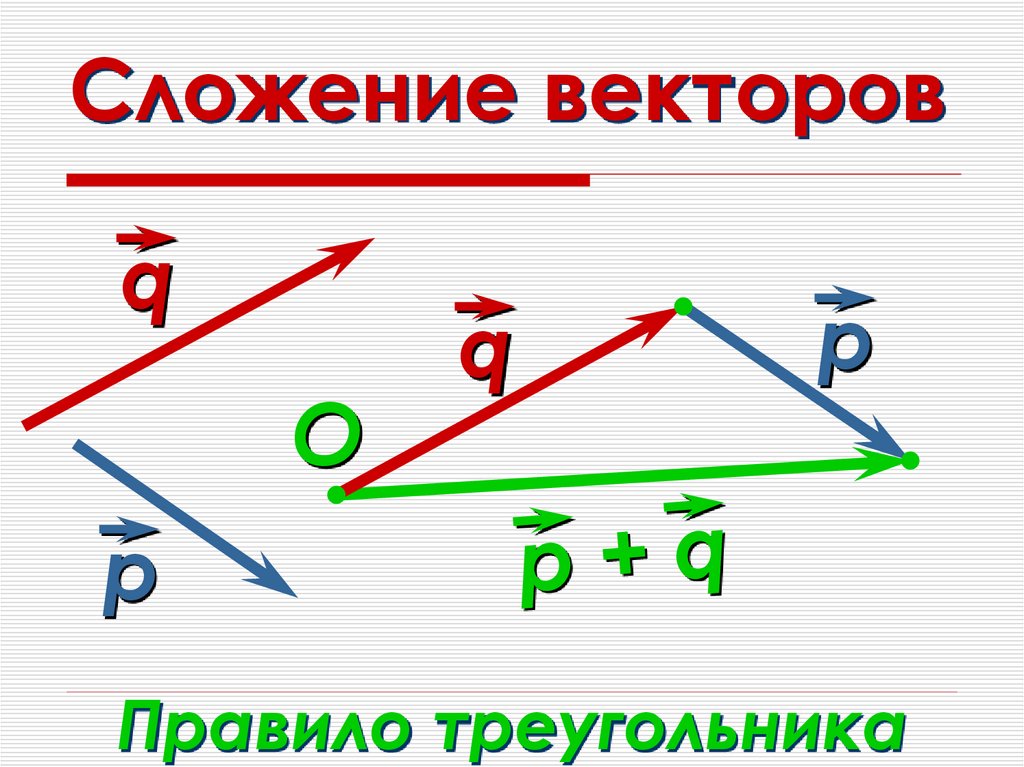
Правило треугольника

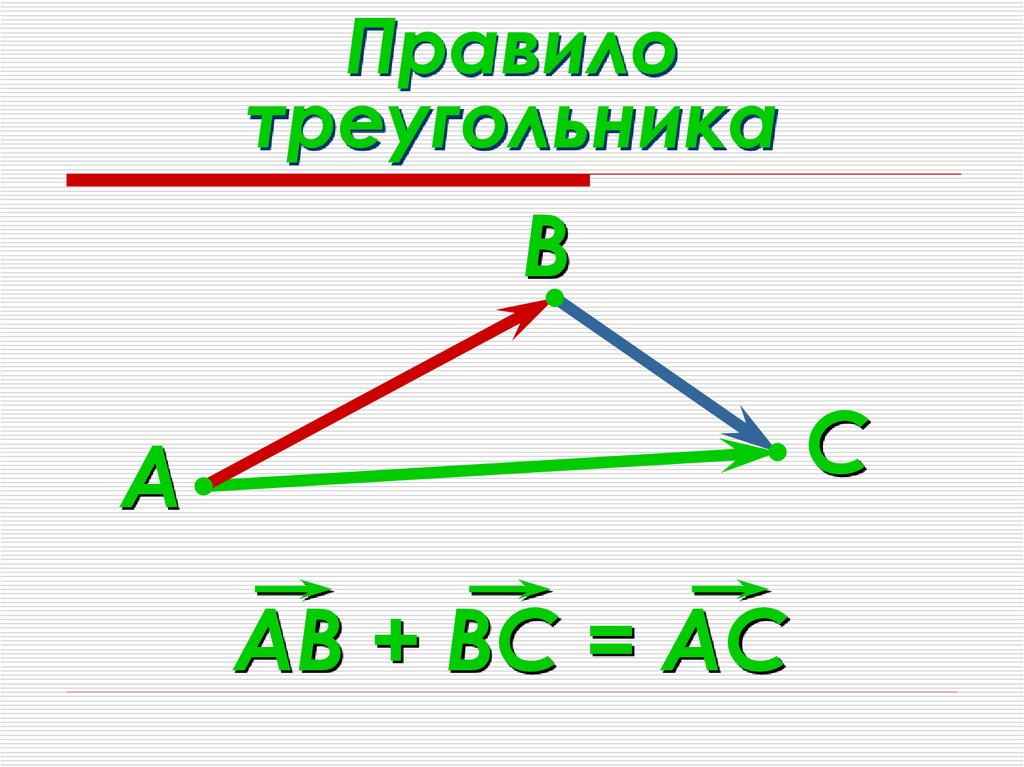
16. Правило треугольника

В
С
А
АВ + ВС = АС

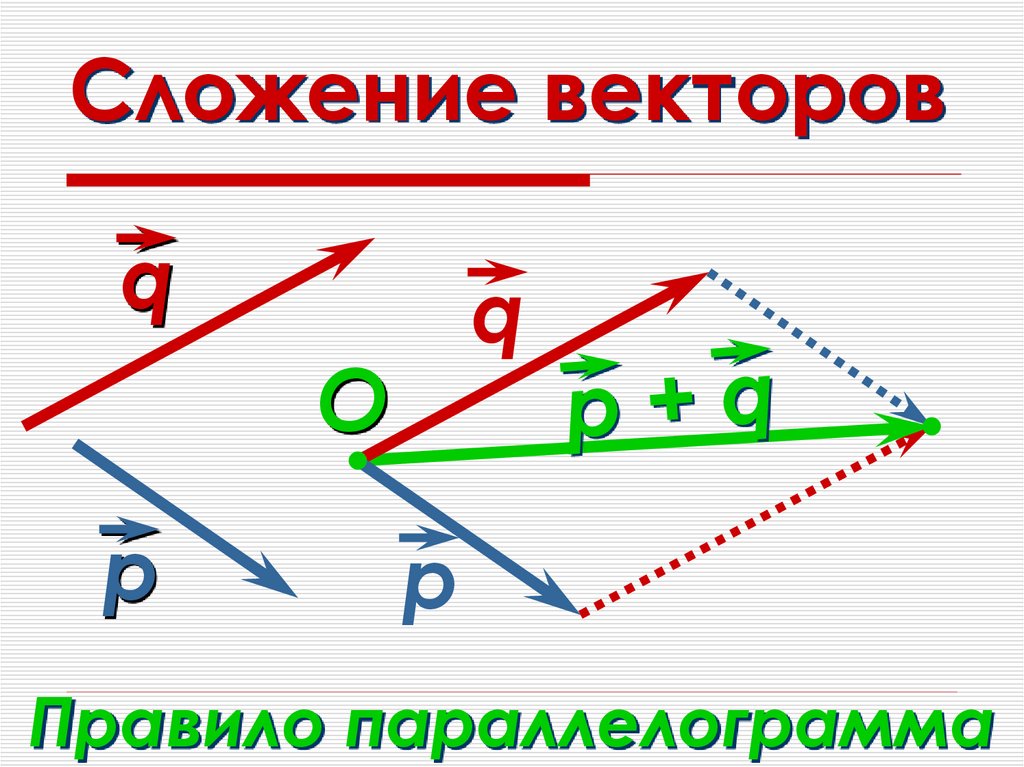
17. Сложение векторов

q
q
O
р
р
Правило параллелограмма

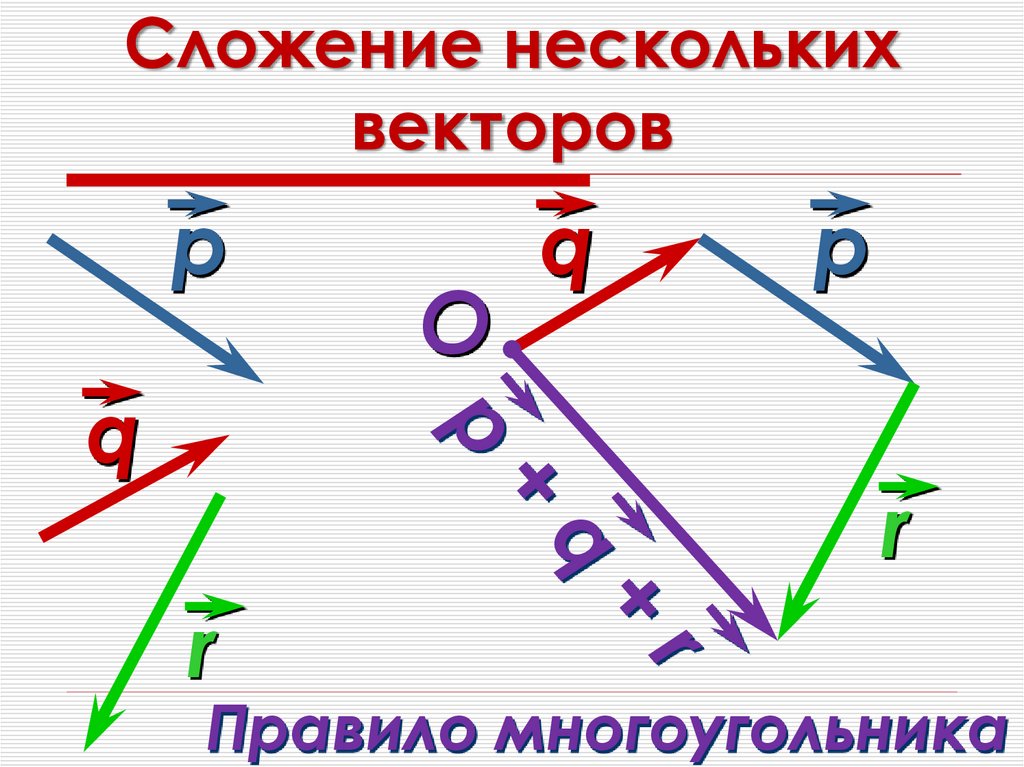
18. Сложение нескольких векторов

р
q
O
q
р
r
r
Правило многоугольника

19. Свойства сложения

а+b= b+a
− переместительный закон
(а + b) + с = (b + с) + a
− сочетательный закон
а − b = a +(− b)
− разность векторов

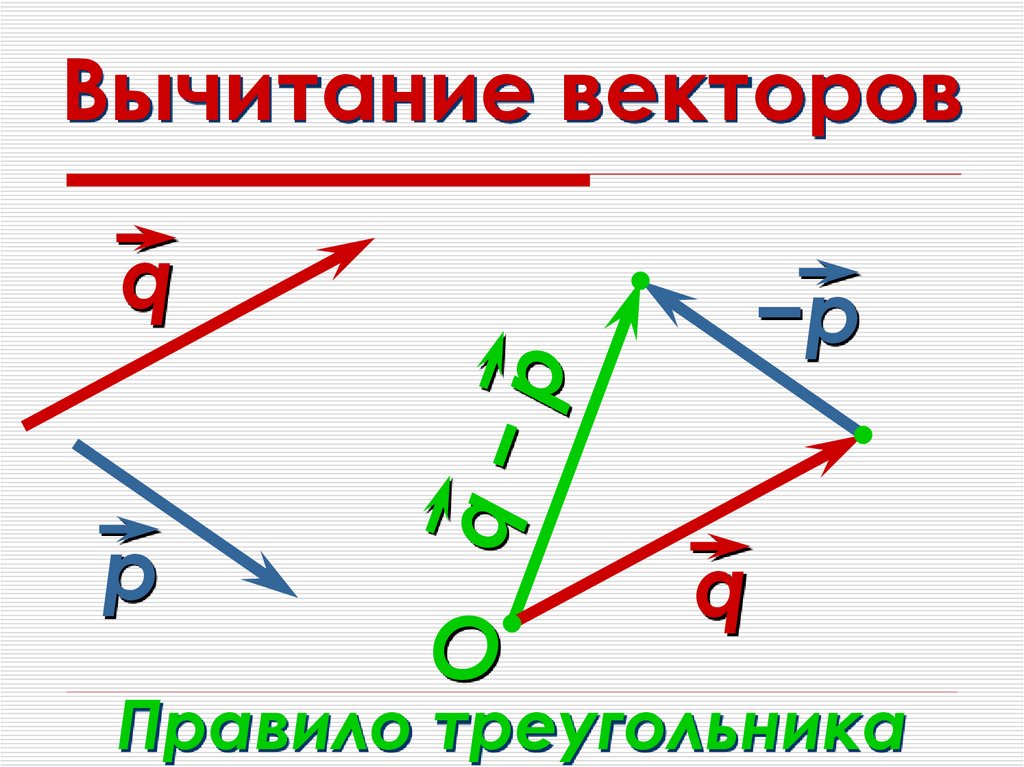
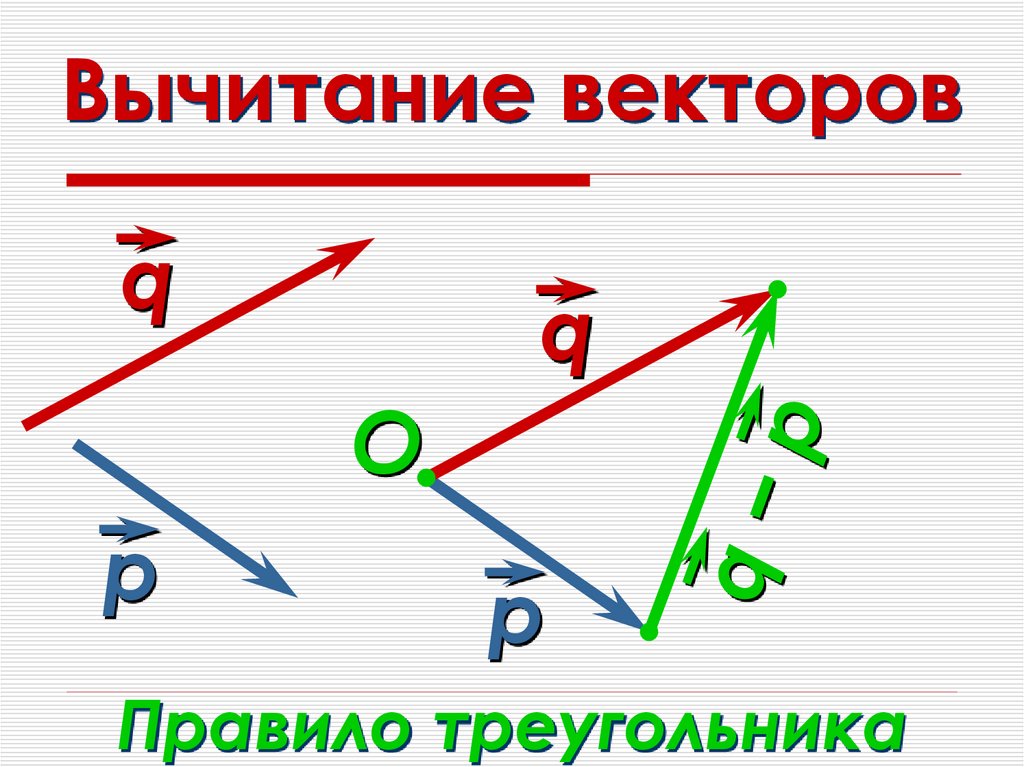
20. Вычитание векторов

q
р
−р
O
q
Правило треугольника

21. Вычитание векторов

q
q
O
р
р
Правило треугольника

22. Сложение векторов в координатной форме

(
)
(
(
)
)

23. Вычитание векторов в координатной форме

(
(
)
(
-
-
)
)

24.

Умножение
вектора на число

25. Умножение вектора на число

Определение:

26. Умножение вектора на число ( векторная форма)

27.

Свойства умножения
Для любых векторов
(kn)а = k(na)
− сочетательный закон
k(а + b) = ka + kb
− первый распределительный закон
(k + n)а = ka + na
− второй распределительный закон

28. Умножение вектора на число ( координатная форма)

Если вектор а имеет координаты(х;у),
то вектор kа имеет координаты
(kх;kу).
Например, а ( 2;-3), 4а (8; -16),
-0,5а (-1; 1,5),

29. Применение векторов к решению задач

30. Задача 1.

Дано: АВ,
С АВ, АС = ВС,
Задача 1.
О – произв. точка
плоскости
1
Доказать: ОС = (ОА + ОВ)
2
А
М
С
О
В
1
ОС = ОМ =
2
1
= (ОА + ОВ)
2

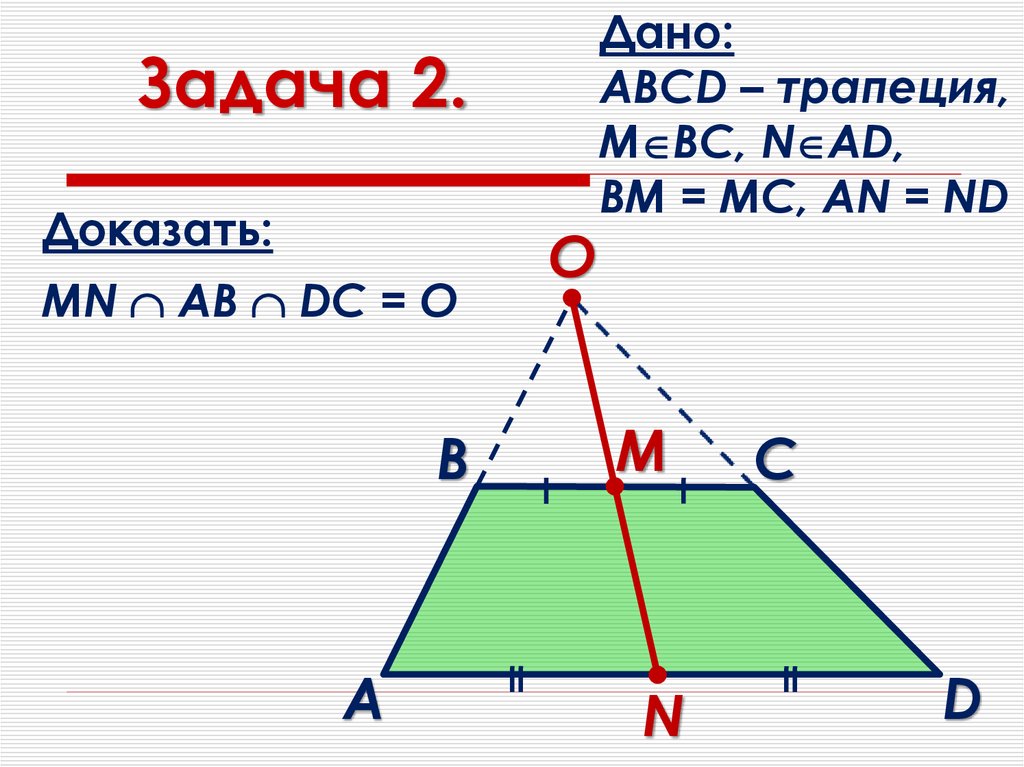
31. Задача 2.

Доказать:
MN AВ DC = O
В
A
О
Дано:
АВСD – трапеция,
М ВС, N AD,
BM = MC, AN = ND
M
N
C
D

32. Средняя линия трапеции

Теорема
Средняя линия трапеции параллельна
основаниям и равна их полусумме.
B
M
A
C
N
D