Вектор - направленный отрезок

1.

Мой первый слог – почтенный срок,
Коль прожит он недаром.
Модель второго – на столе,
Румяна, с пылу, с жару.
Меня вы встретите везде –
Такой я вездесущий.
А имя громкое мое –
Латинское «несущий».

2.

ВЕКТОРЭТО НАПРАВЛЕННЫЙ ОТРЕЗОК
ВЕКТОР АВ

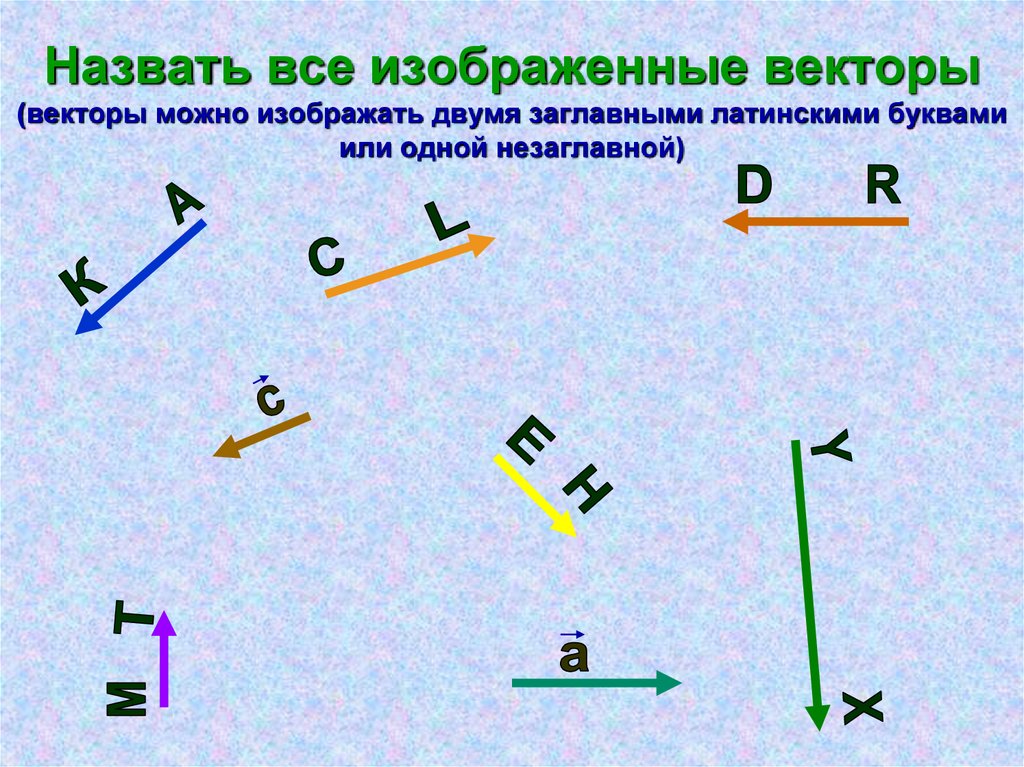
3. Назвать все изображенные векторы (векторы можно изображать двумя заглавными латинскими буквами или одной незаглавной)

4. Нулевой вектор

Любая точка на плоскости может
рассматриваться как вектор.
Такой вектор называется нулевым.
М
ММ = 0

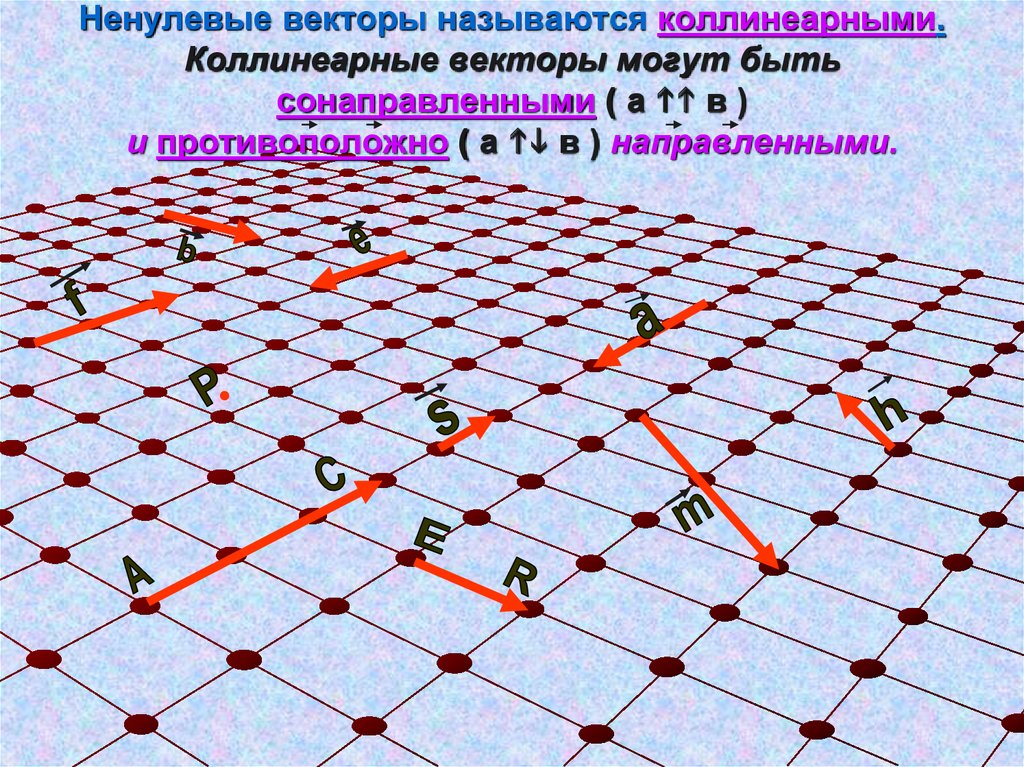
5. Ненулевые векторы называются коллинеарными. Коллинеарные векторы могут быть сонаправленными ( а  в ) и противоположно ( а 

Ненулевые векторы называются коллинеарными.
Коллинеарные векторы могут быть
сонаправленными ( а в )
и противоположно ( а в ) направленными.

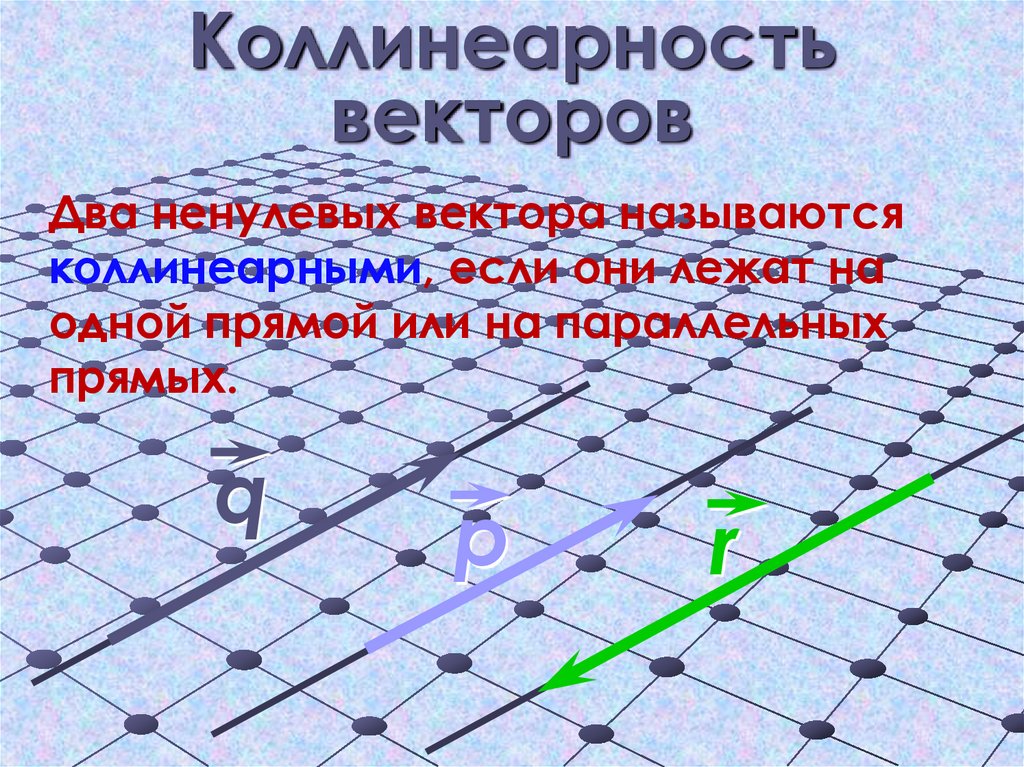
6. Коллинеарность векторов

Два ненулевых вектора называются
коллинеарными, если они лежат на
одной прямой или на параллельных
прямых.
q
р
r

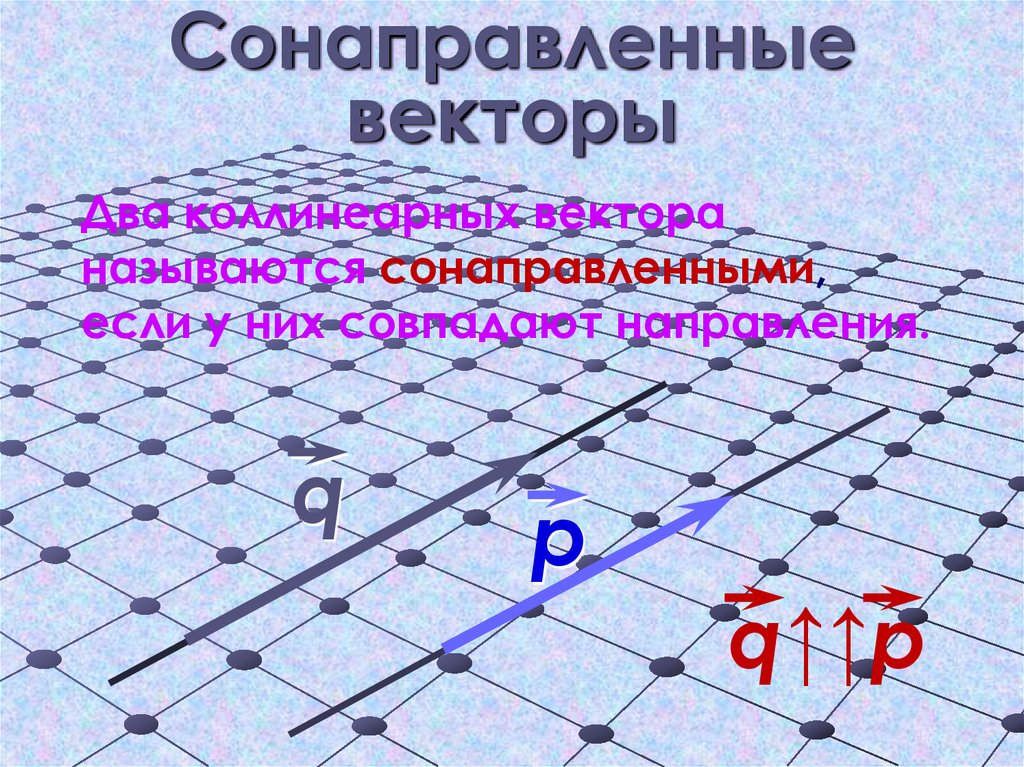
7. Сонаправленные векторы

Два коллинеарных вектора
называются сонаправленными,
если у них совпадают направления.
q
р
q↑↑р

8. Противоположно направленные векторы

Два коллинеарных вектора называются
противоположно направленными, если
они не сонаправлены.
а
b
a↑↓b

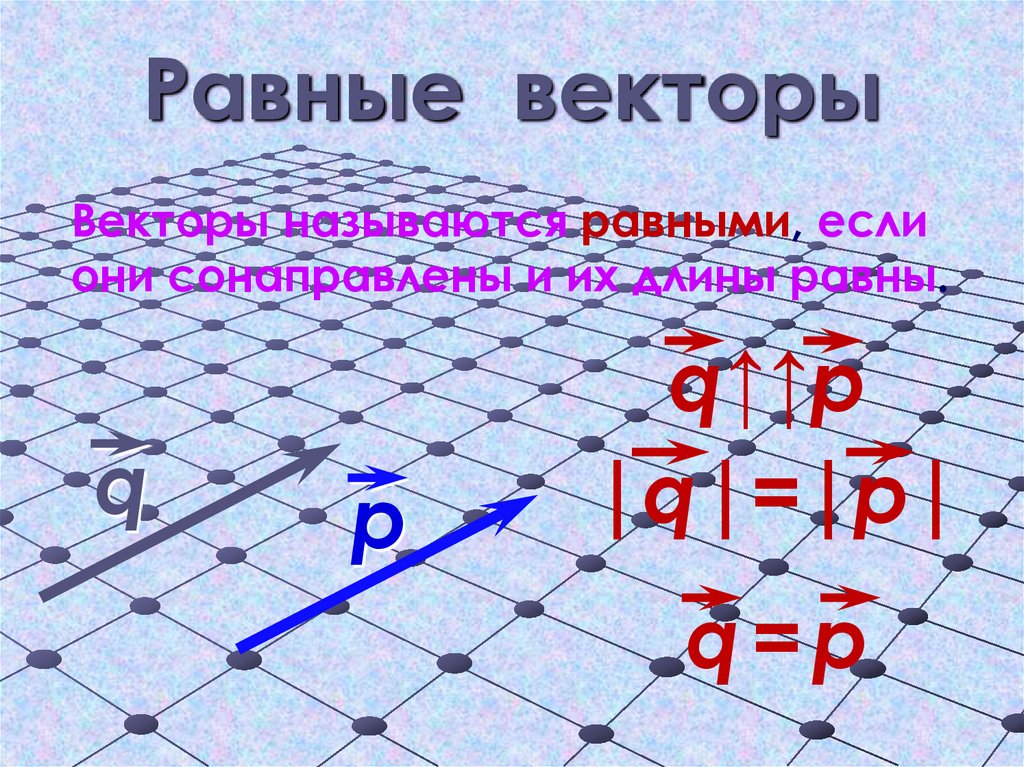
9. Равные векторы

Векторы называются равными, если
они сонаправлены и их длины равны.
q
р
q↑↑р
|q|=|р|
q=р

10. Откладывание вектора от данной точки

От любой точки М можно отложить
вектор, равный данному вектору а, и
притом только один.
А
a
М
В
N

11. Длина вектора

Длиной ненулевого вектора АВ
называется длина отрезка АВ.
В
|АВ|=|а|
а
А
0
|0|= 0

12. Проверь себя

1.Что называется вектором?
а)любой отрезок
б)отрезок, обозначенный двумя заглавными латинскими буквами
в) отрезок с выбранным направлением
2. Какой вектор является нулевым?
а)длина вектора равна 0
б)вектор лежит на прямой
в)вектор обозначен одной буквой
3. Векторы коллинеарны, если…
а)лежат на прямых
б)один из них ненулевой
в)один из векторов нулевой
4. Векторы неколлинеарны, если…
а)лежат на одной прямой
б)лежат на разных прямых
в)они ненулевые и лежат на двух пересекающихся прямых
5. Векторы называются равными, если …
а)их длины равны
б)их модули равны и векторы направлены в одну сторону
в)они отложены от одной точки

13.

Сложение векторов
Вычитание векторов
Умножение вектора на число
Скалярное умножение векторов

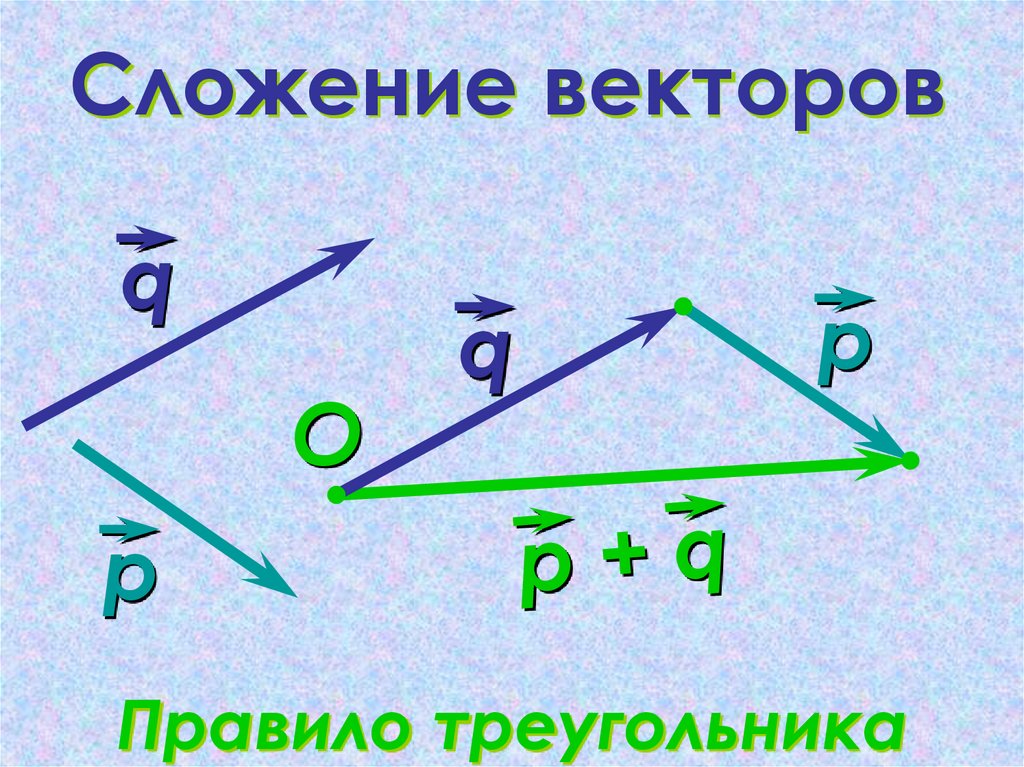
14. Сложение векторов

q
O
q
р
р
Правило треугольника

15. Сложение векторов

q
O
q
р
р
Правило треугольника

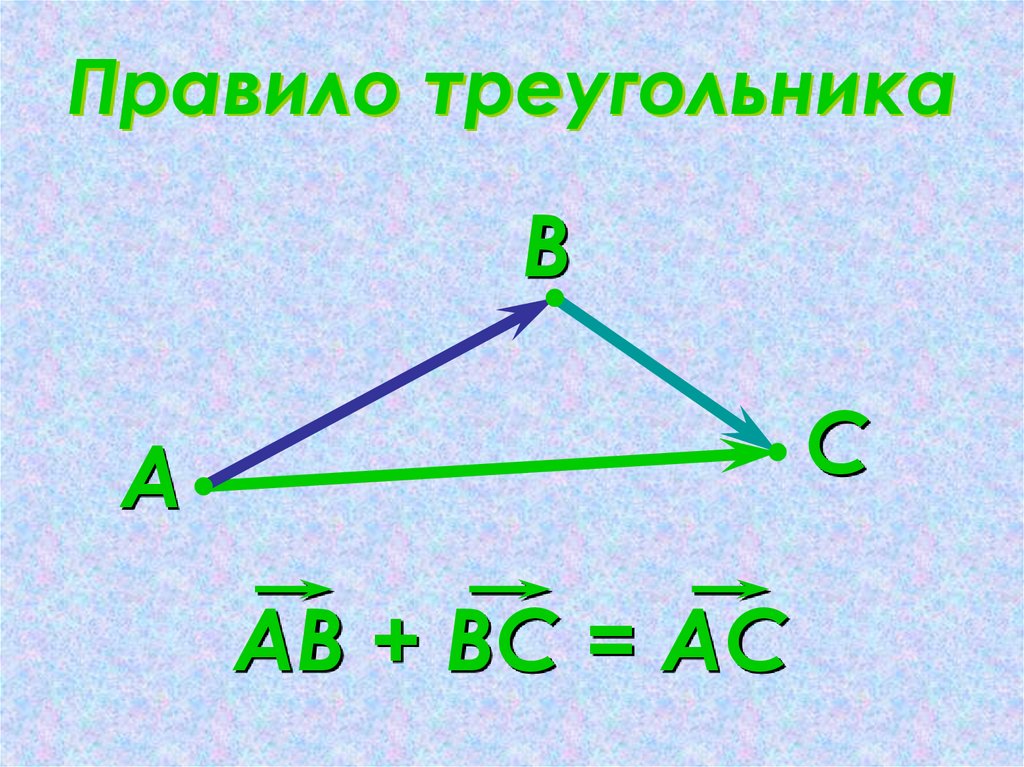
16. Правило треугольника

В
С
А
АВ + ВС = АС

17. Сложение векторов, если векторы имеют общее начало

q
q
O
р
р
Правило параллелограмма

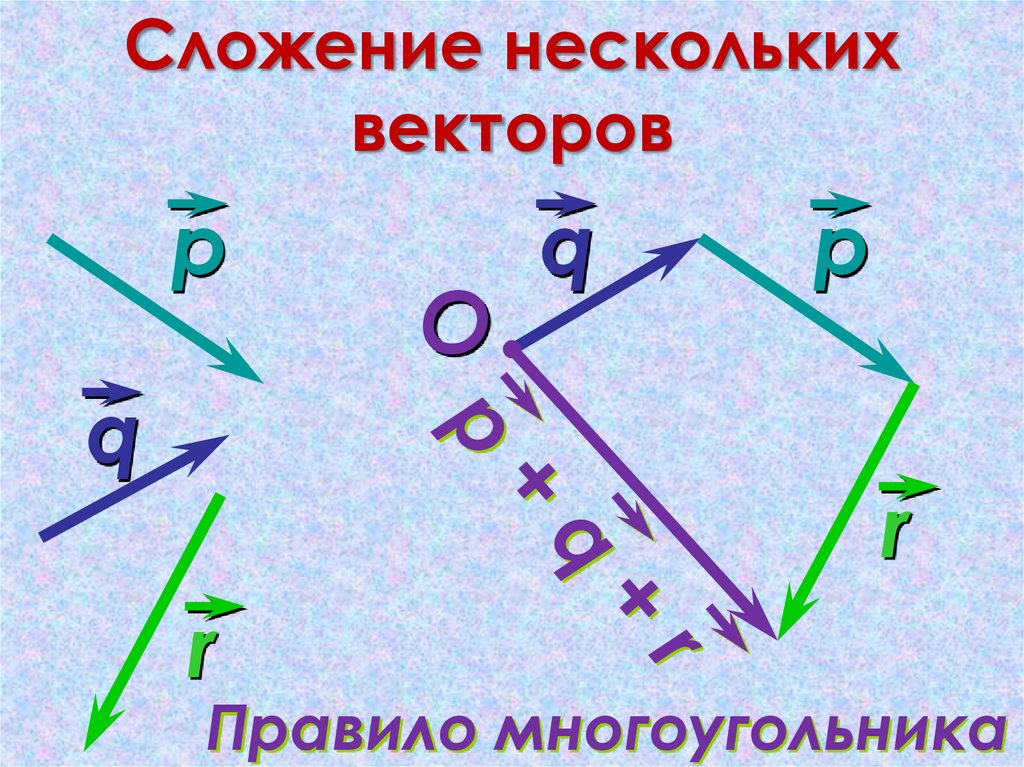
18. Сложение нескольких векторов

р
q
O
q
р
r
r
Правило многоугольника

19. Свойства сложения

а+b= b+a
− переместительный закон
(а + b) + с = (b + с) + a
− сочетательный закон
а − b = a +(− b)
− разность векторов

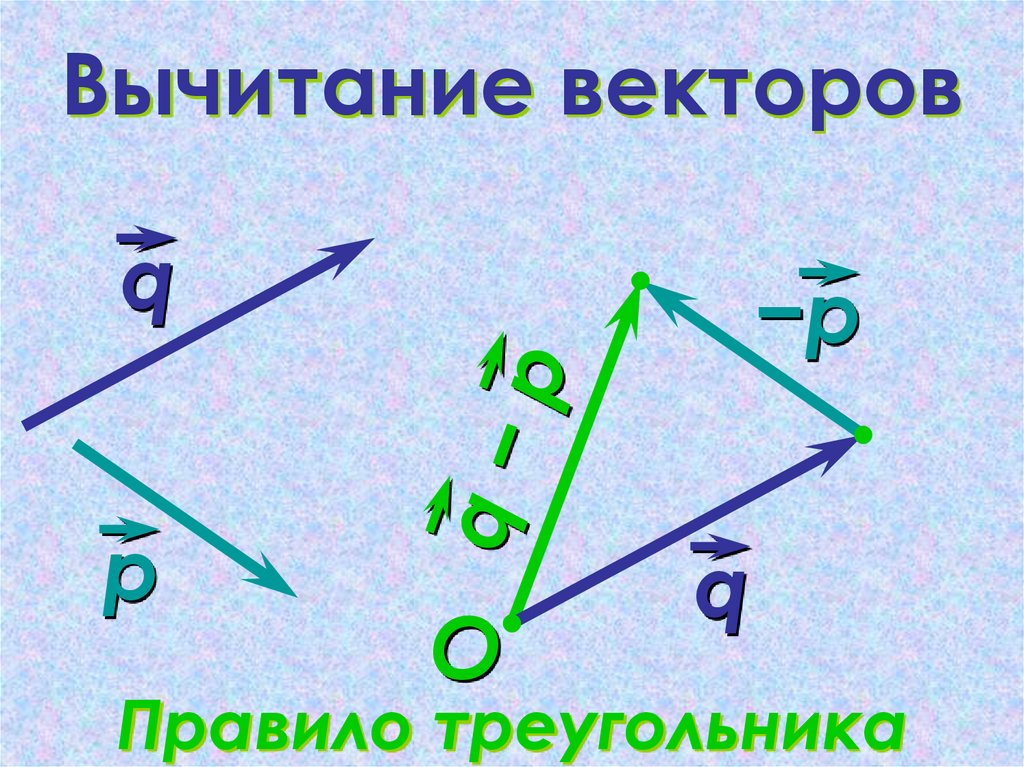
20. Вычитание векторов

q
р
−р
O
q
Правило треугольника

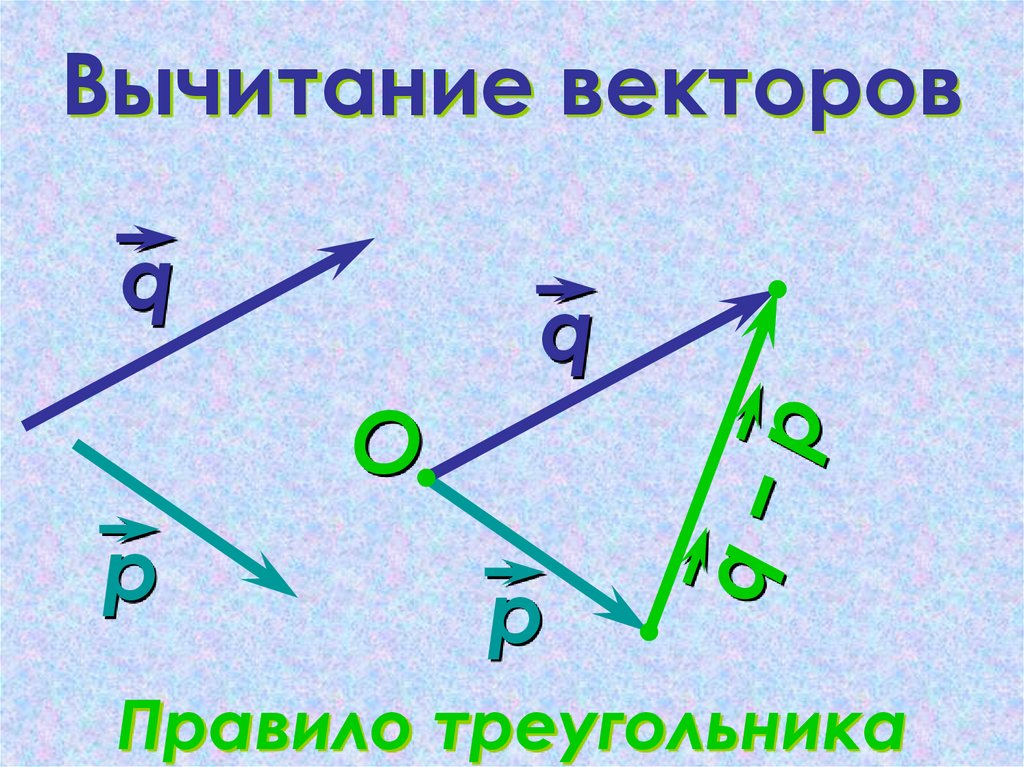
21. Вычитание векторов

q
q
O
р
р
Правило треугольника

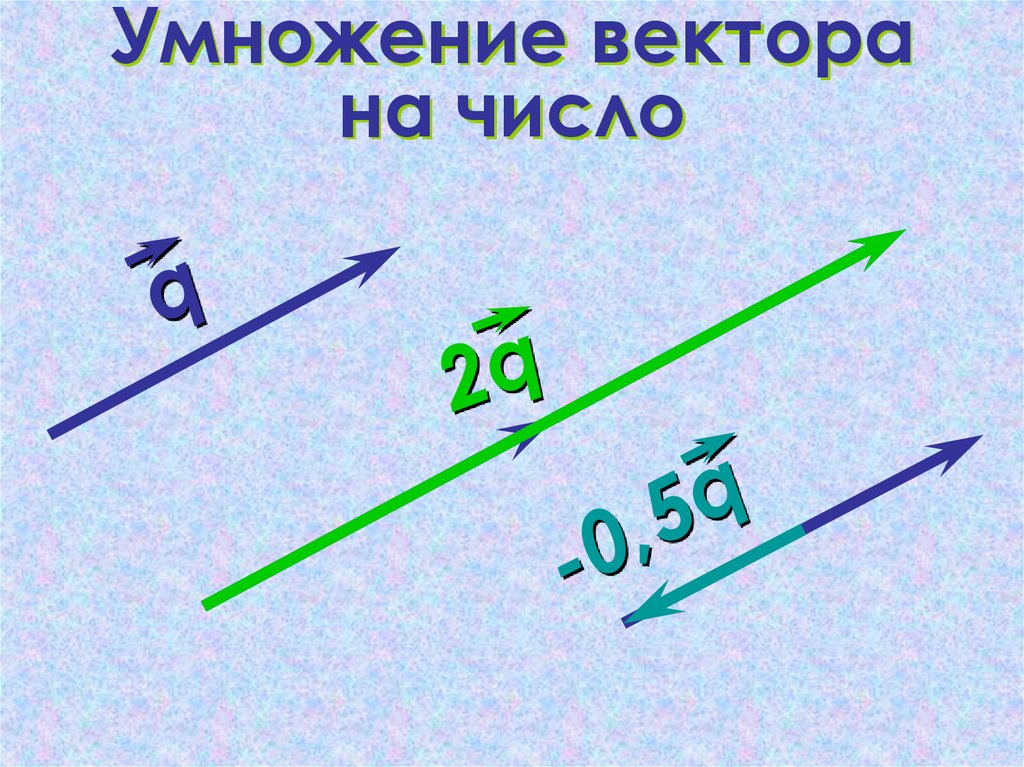
22. Умножение вектора на число

23.

Свойства умножения
(kn)а = k(na)
− сочетательный закон
k(а + b) = ka + kb
− первый распределительный закон
(k + n)а = ka + na
− второй распределительный закон