Similar presentations:
Биофизика клетки. Липиды как жидкие кристаллы
1.
Биофизика клетки:одиннадцатая лекция
Рассматриваемые вопросы:
1. Липиды как жидкие кристаллы
2. Теория упругости липидных мембран: модель Хельфриха
3. Понятие кривизны; энергия сферы и цилиндра
4. Спонтанная кривизна липидов
5. Энергия нанотрубки; равновесный радиус нанотрубки
2. Локальные различия в кривизне поверхности – отличительная черта клеточных мембран
Endosomeфенестрации в
аппарате Гольджи
Golgi
MVB
ER
Тубулы на
эндосомах
Отпочкование
вирионов HIV
3. Эндоциоз – характерный пример формирования сильно искривленных структур
Rvesicle ~ 20-50 nmEvesicle = 8πK (K – bending modulus)
Evesicle = 500kBT per vesicle
cytoplasm
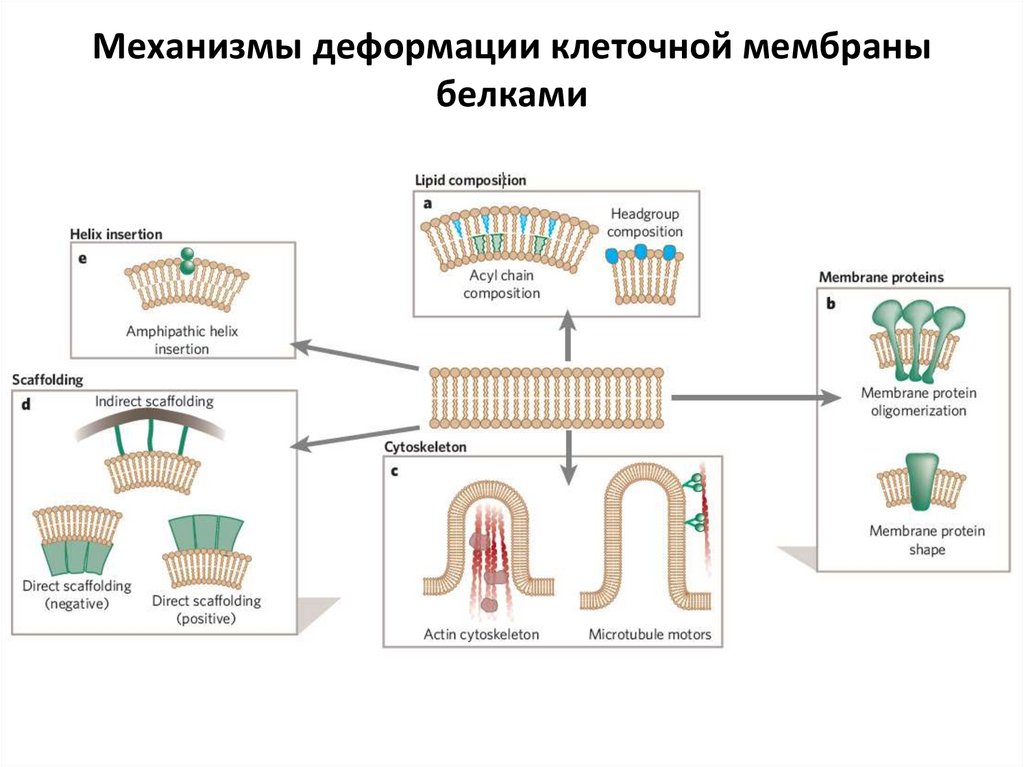
4. Механизмы деформации клеточной мембраны белками
5.
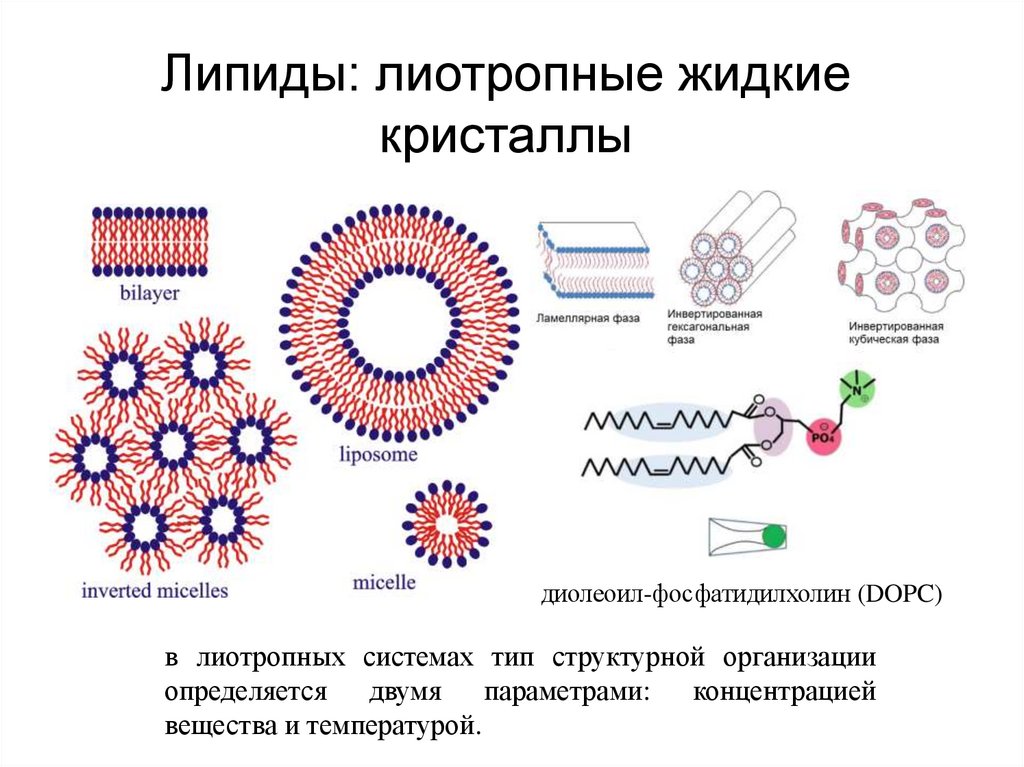
Липиды: лиотропные жидкиекристаллы
диолеоил-фосфатидилхолин (DOPC)
в лиотропных системах тип структурной организации
определяется двумя параметрами: концентрацией
вещества и температурой.
6.
Микрофотографии жидких кристалловТемпература, при которой твердая фаза переходит в мезофазу,
называется температурой плавления Тпл, а температура перехода
мезофазы в изотропную жидкость температурой просветления, Тпр.
7.
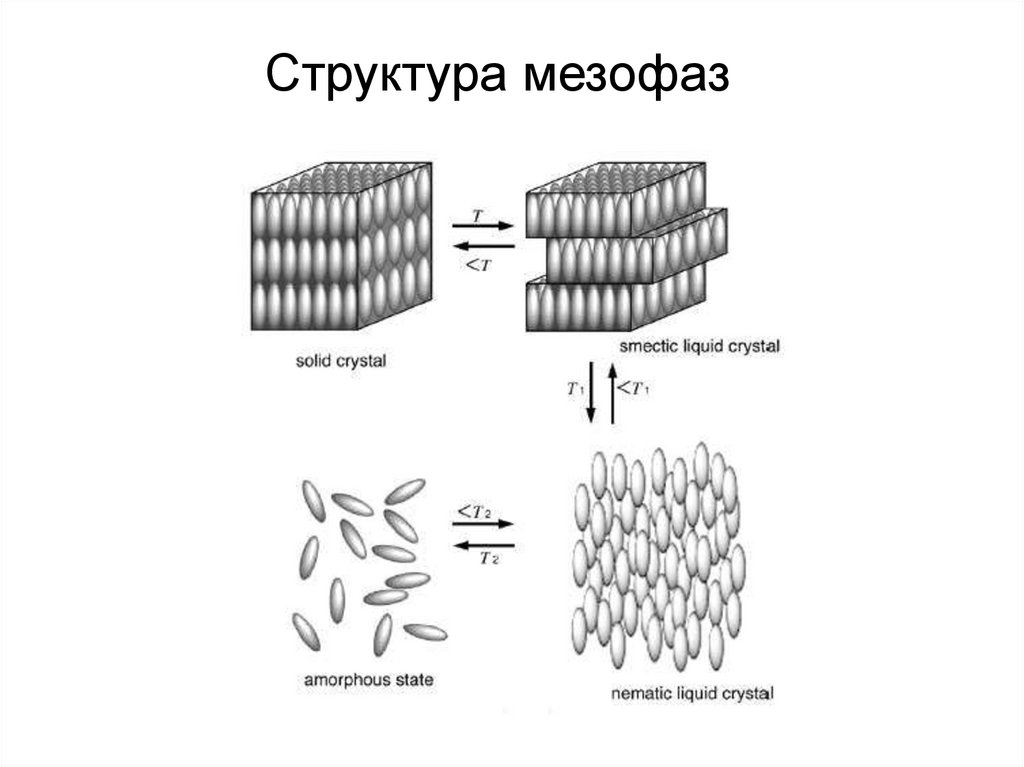
Структура мезофаз8.
Классификация мезофаз: смектикиСмектики: центры масс молекул располагаются в слоях, но оси не лежат в
плоскости слоя.
1) С неструктурными слоями:
1.1) Смектик А (оси перпендикулярны слоям);
1.2) Смектик С (оси наклонены);
1.3) Смектик С* (оси наклонены,
спиральное упорядочение);
2) Со структурными слоями:
2.1) Смектик В (гексагональная гранецентрированная решетка
в слоях, оси перпендикулярны слоям);
2.2) Смектик Н (та же решетка, оси наклонены);
2.3) Смектик Н* (то же + спиральное упорядочение);
2.4) Смектик Е (ромбическая решетка, затруднено вращение
вокруг длинных осей, оси перпендикулярны слоям);
2.5) Смектик G (то же, но оси наклонены).
9.
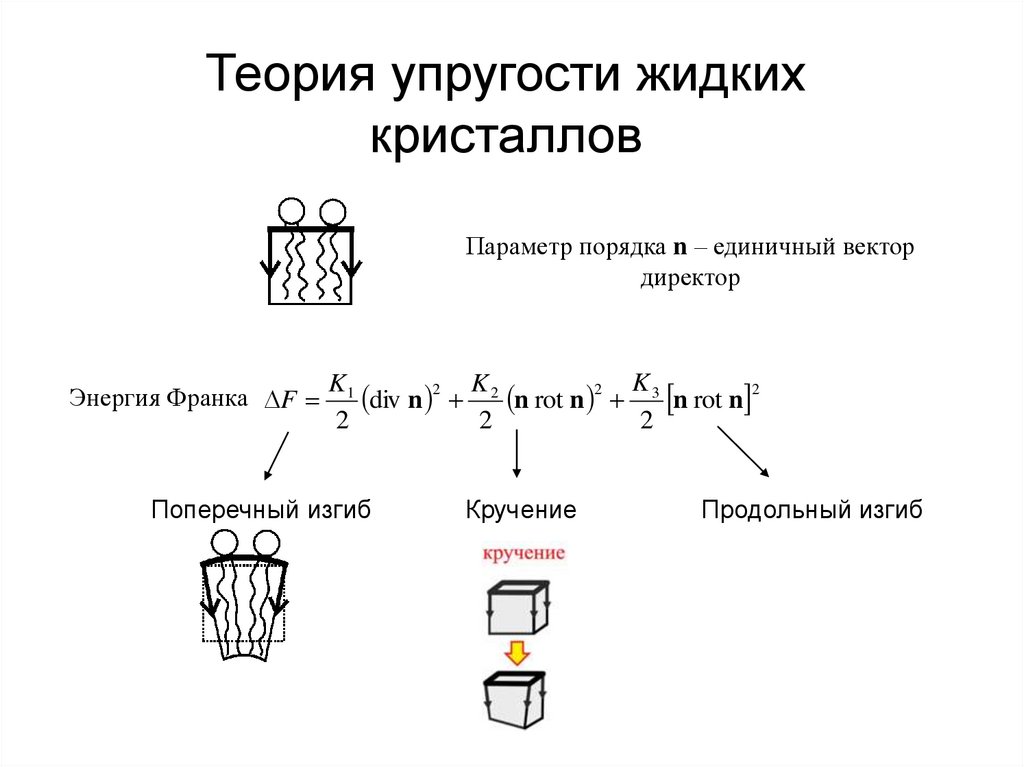
Теория упругости жидкихкристаллов
Параметр порядка n – единичный вектор
директор
Энергия Франка F
K1
div n 2 K 2 n rot n 2 K 3 n rot n 2
2
2
2
Поперечный изгиб
Кручение
Продольный изгиб
10.
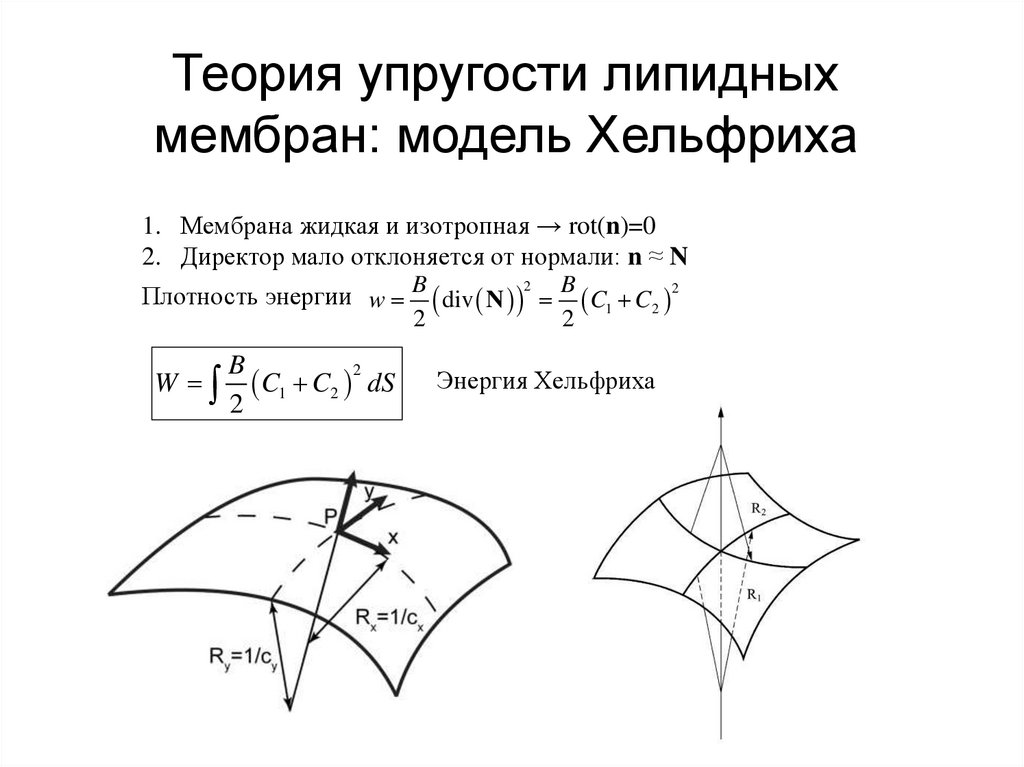
Теория упругости липидныхмембран: модель Хельфриха
1. Мембрана жидкая и изотропная → rot(n)=0
2. Директор мало отклоняется от нормали: n ≈ N
2
Плотность энергии w B div N B C1 C2 2
2
2
W
B
2
C
C
1 2 dS
2
Энергия Хельфриха
11.
Энергия ХельфрихаB 2
2
B
W C1 C2 C0 C0 dS
2
2
суммарная кривизна
мембраны равна C1+C2
спонтанная кривизна липида:
кривизна мембраны, состоящей
только из липидов данного сорта,
в отсутствие внешних сил
поверхностное натяжение:
энергия единицы поверхности
мембраны без учета кривизны
12.
Определение модуля изгибаR0
Rp
Evans, E., & Rawicz, W. (1990). Entropy-driven tension and bending elasticity in
condensed-fluid membranes. Physical review letters, 64(17), 2094.
Зависимость натяжения от увеличения видимой
площади приближается экспонентой, откуда
определяется модуль изгиба B.
B = 20 kBT
13.
Энергия изгиба сферы и цилиндраДля сферы радиуса R:
2
B
B 1 1
2
W C1 C2 dS dS
2
2 R R
B 4
B 4
2
dS
4
R
8 B 500k BT
2
2
2R
2R
Для цилиндра радиуса R длины L:
2
B
B 1
2
W C1 C2 dS 0 dS
2
2 R
B 1
B 1
BL
dS
2 RL
2
2
2R
2R
R
14.
Спонтанная кривизна липидовB
2
W C1 C2 C0 dS
2
15.
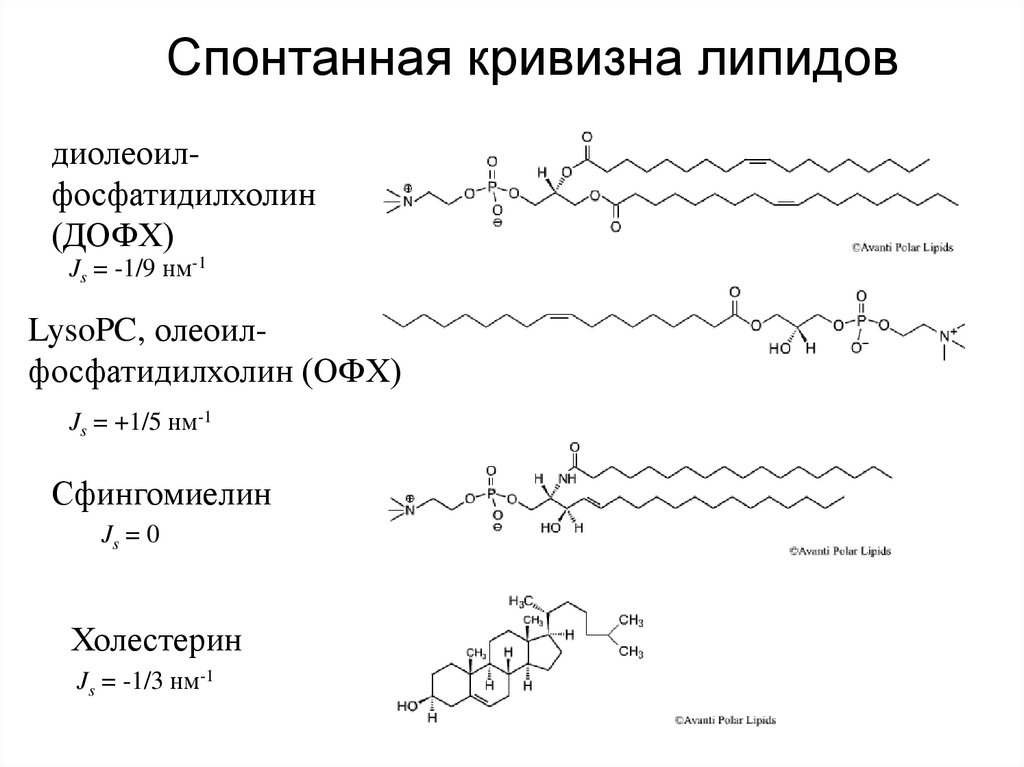
Спонтанная кривизна липидовдиолеоилфосфатидилхолин
(ДОФХ)
Js = -1/9 нм-1
LysoPC, олеоилфосфатидилхолин (ОФХ)
Js = +1/5 нм-1
Сфингомиелин
Js = 0
Холестерин
Js = -1/3 нм-1
16.
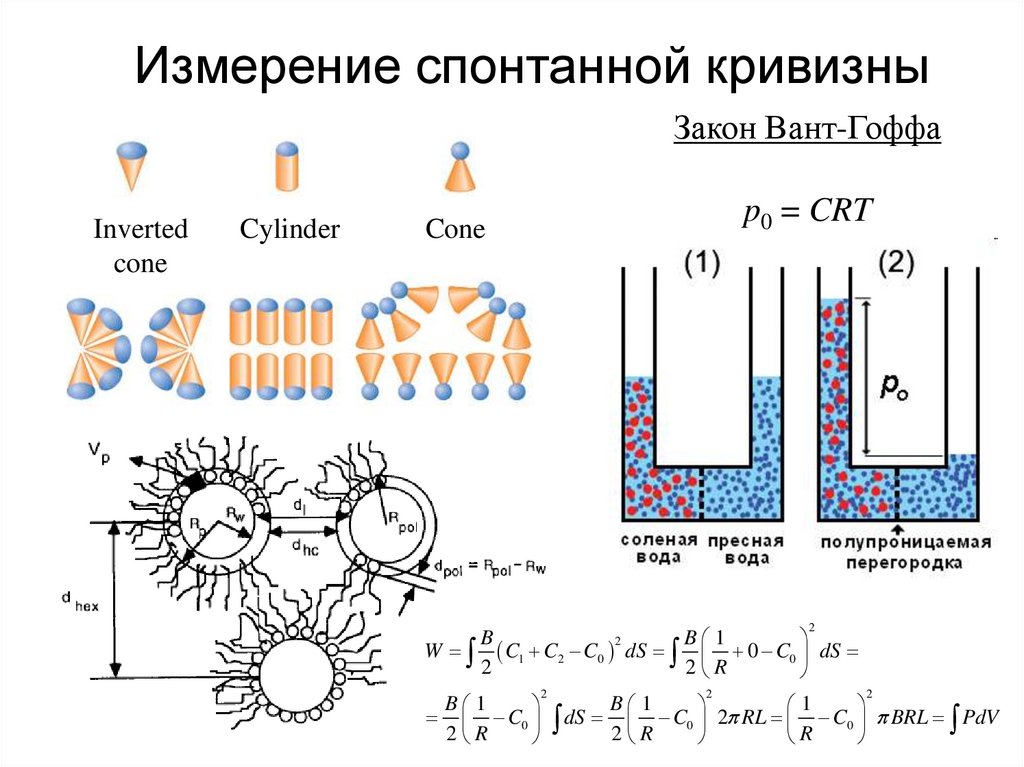
Измерение спонтанной кривизныЗакон Вант-Гоффа
Inverted
cone
Cylinder
p0 = CRT
Cone
2
B
B 1
2
W C1 C2 C0 dS 0 C0 dS
2
2 R
2
2
2
B 1
B 1
1
C0 dS C0 2 RL C0 BRL PdV
2 R
2 R
R
17.
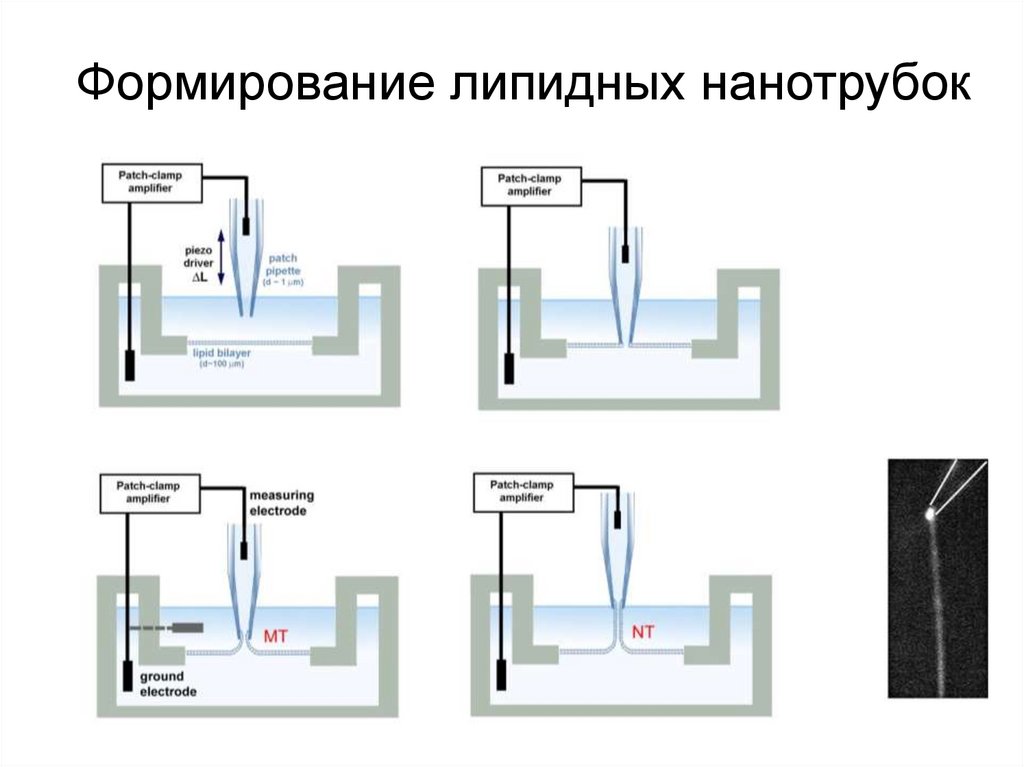
Формирование липидных нанотрубок18. Образование нанотрубки при коллапсе мембранной трубки
Формирование нанотрубкиДестабилизация
мембранного перешейка
R1
r
R2
МТ
НТ
r
L
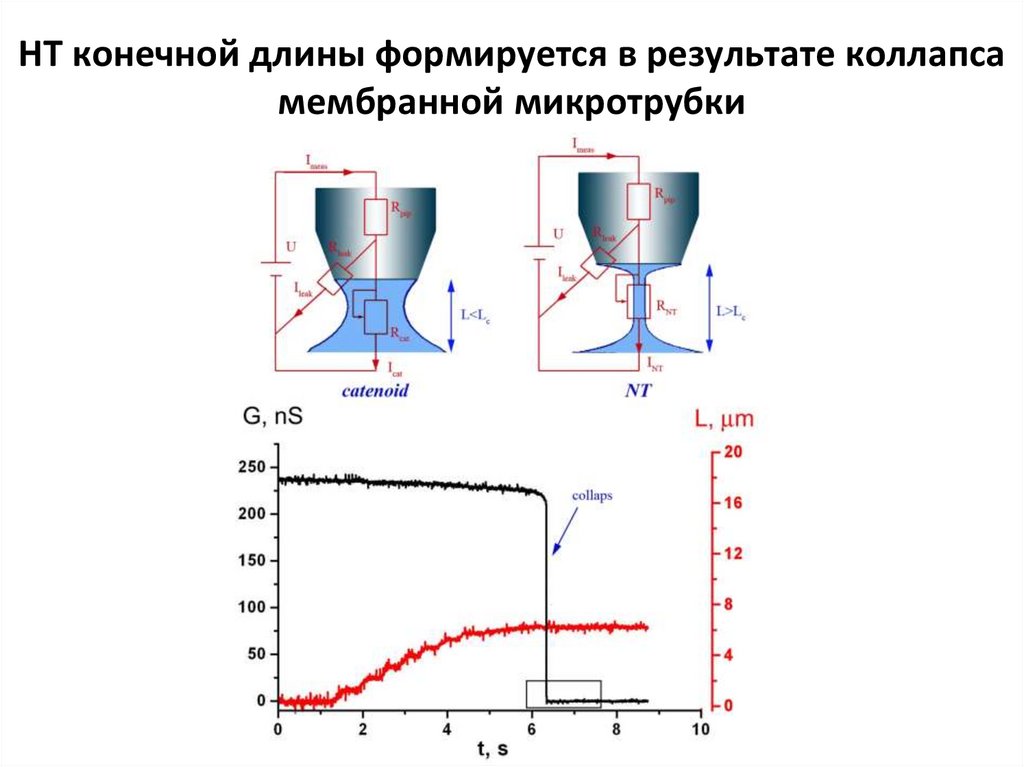
19. НТ конечной длины формируется в результате коллапса мембранной микротрубки
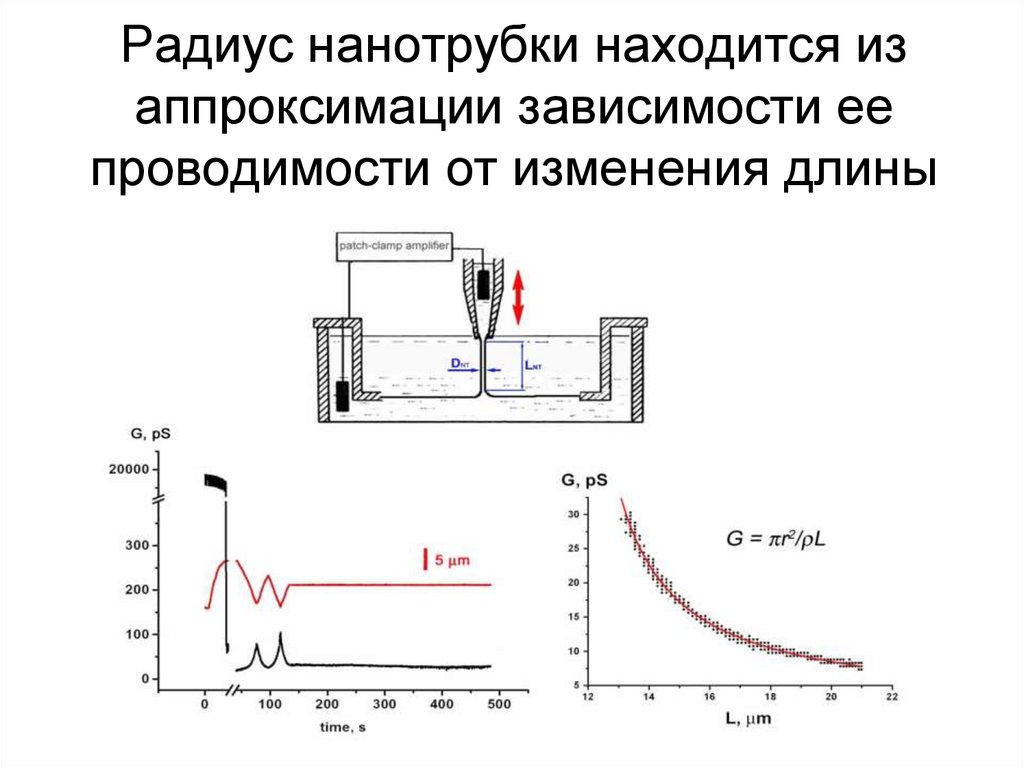
20. Радиус нанотрубки находится из аппроксимации зависимости ее проводимости от изменения длины
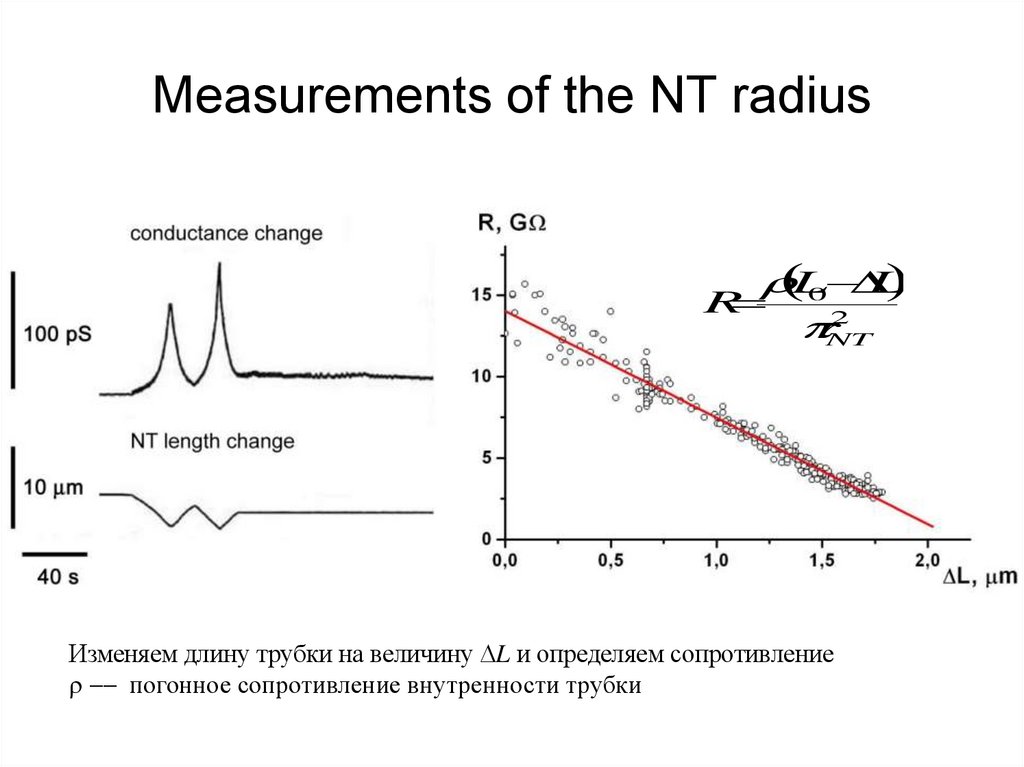
21. Measurements of the NT radius
L0L
R
2
rNT
Изменяем длину трубки на величину L и определяем сопротивление
погонное сопротивление внутренности трубки
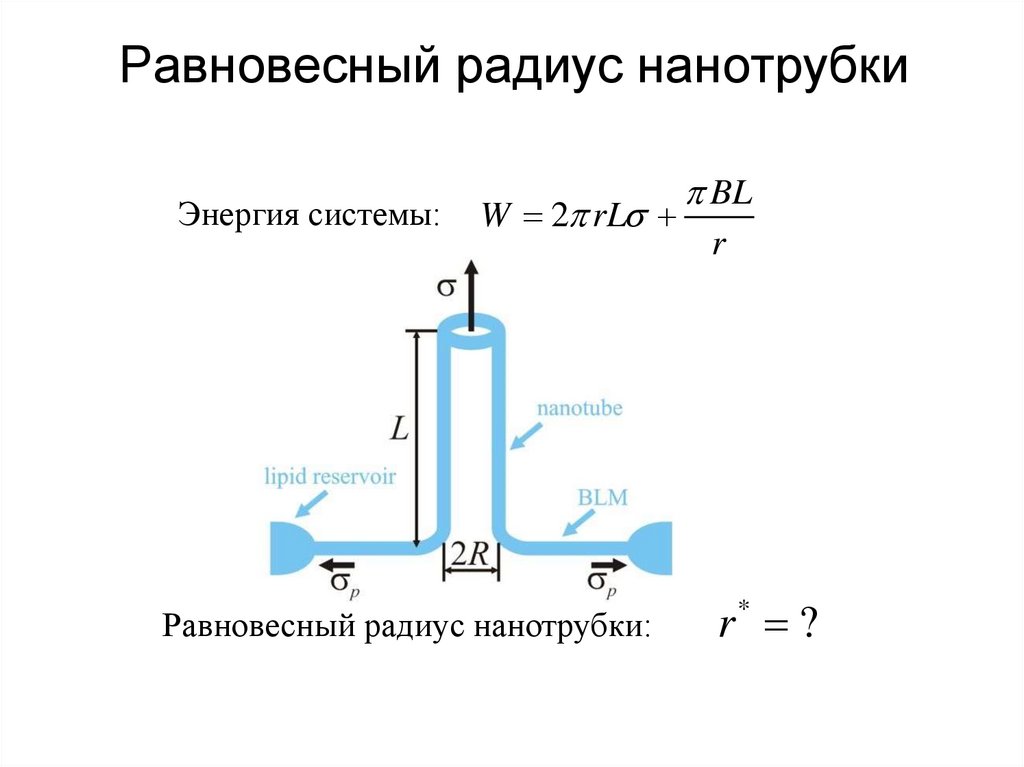
22.
Равновесный радиус нанотрубкиЭнергия системы:
W 2 rL
Равновесный радиус нанотрубки:
BL
r
r* ?
23.
Равновесный радиус нанотрубкиЭнергия системы:
W 2 rL
Равновесный радиус нанотрубки:
BL
r
r*
B
2
Задача. Характерные (для бислоя) величины B 20 kT,
0 1 дин/см; найти r*
Из полученного значения радиуса можно
вычислить только отношение модуля изгиба
мембраны к латеральному натяжению.
24.
Равновесный радиус нанотрубкиЭнергия системы:
W 2 rL
BL
r
B
Равновесный радиус нанотрубки: r
2
Подставляя характерные (для бислоя) величины B 20 kT,
0 1 дин/см, получим r* 6,3 нм.
*
Задача: найти равновесную энергию
системы, т.е. энергию, соответствующую r*
B 20 kT, 0 1 дин/см.
25.
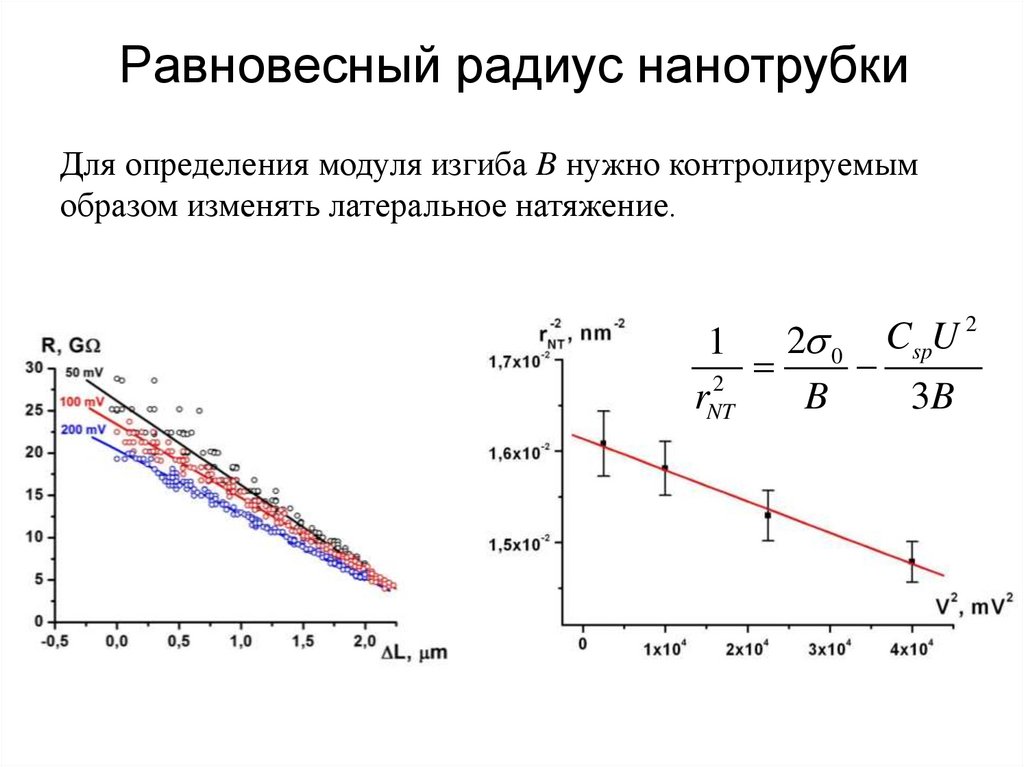
Равновесный радиус нанотрубкиДля определения модуля изгиба B нужно контролируемым
образом изменять латеральное натяжение.
2 0
1
2
rNT
B
3B
CspU 2
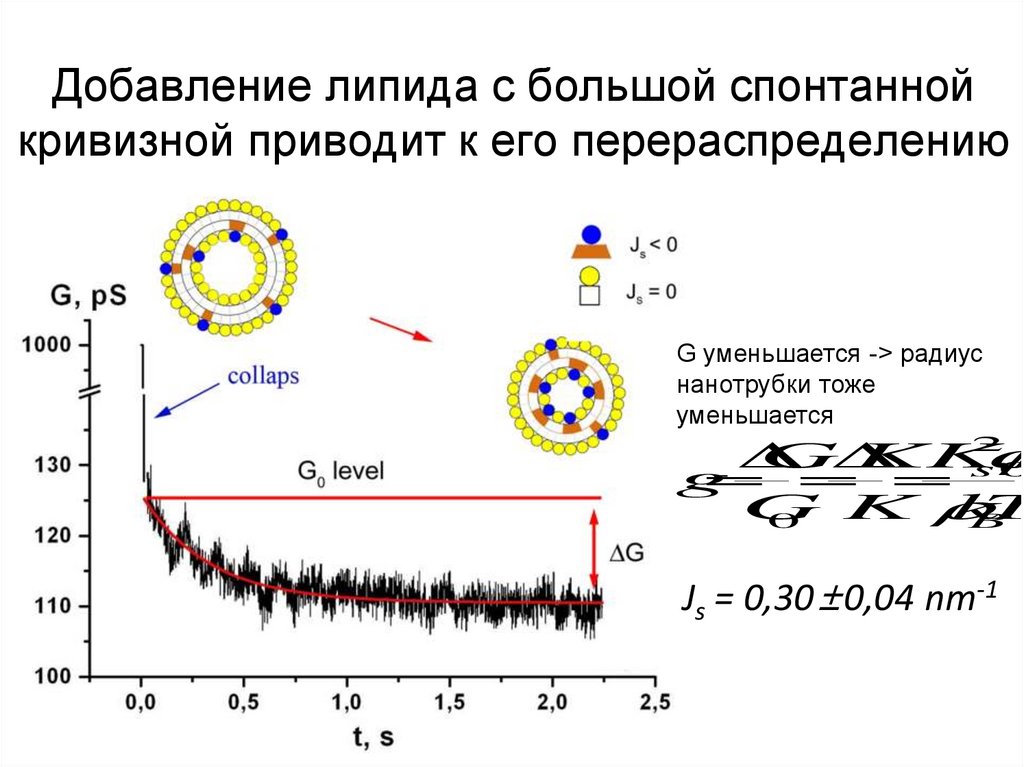
26. Добавление липида с большой спонтанной кривизной приводит к его перераспределению
G уменьшается -> радиуснанотрубки тоже
уменьшается
2
G
KKJ
s
g
0
G
K
k
T
0
B
Js = 0,30±0,04 nm-1
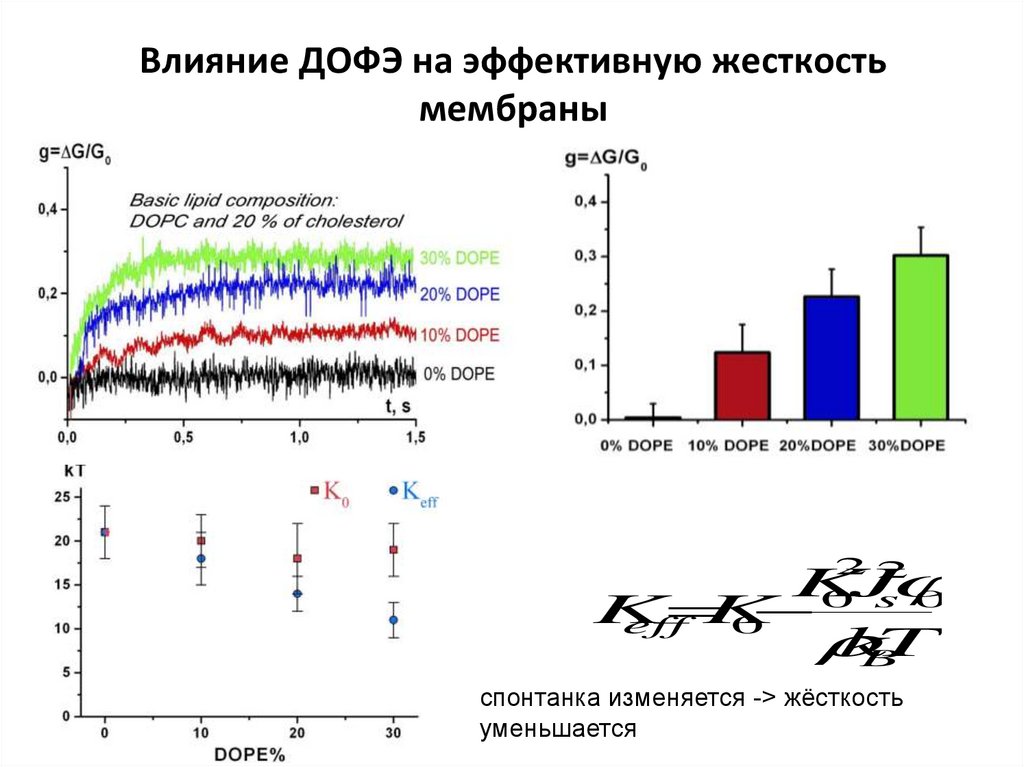
27. Влияние ДОФЭ на эффективную жесткость мембраны
KJK
K
eff
0
k
T
B
22
0 s 0
спонтанка изменяется -> жёсткость
уменьшается
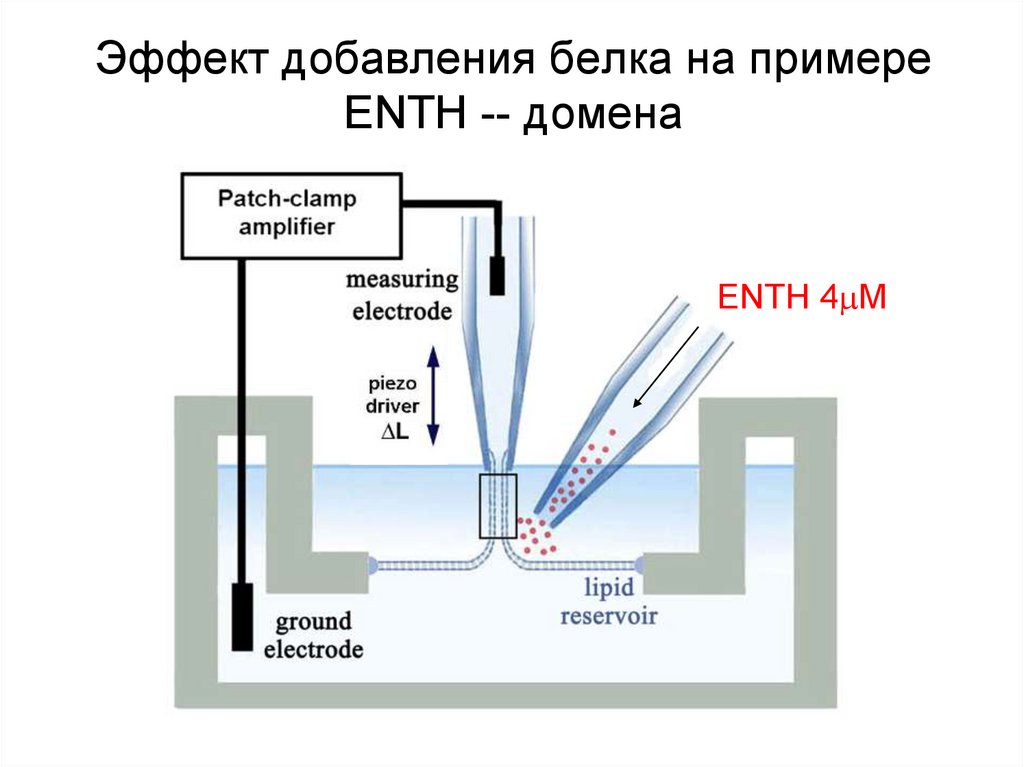
28. Эффект добавления белка на примере ENTH -- домена
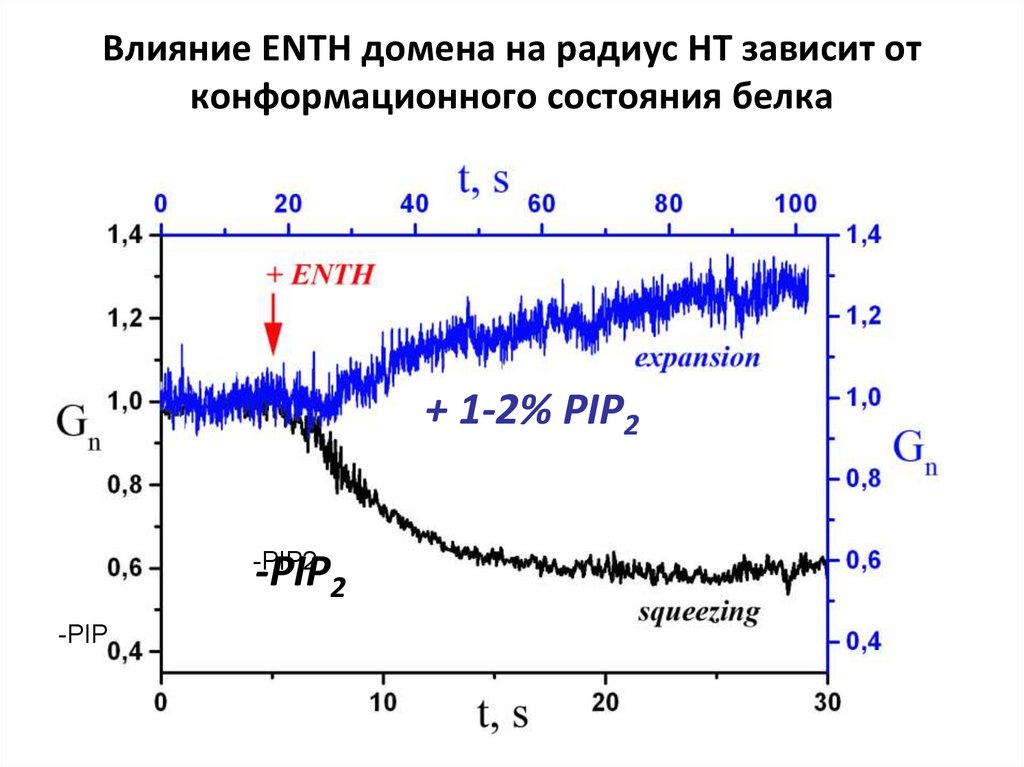
ENTH 4 M29. Влияние ENTH домена на радиус НТ зависит от конформационного состояния белка
+ 1-2% PIP2-PIP2
-PIP2
-PIP
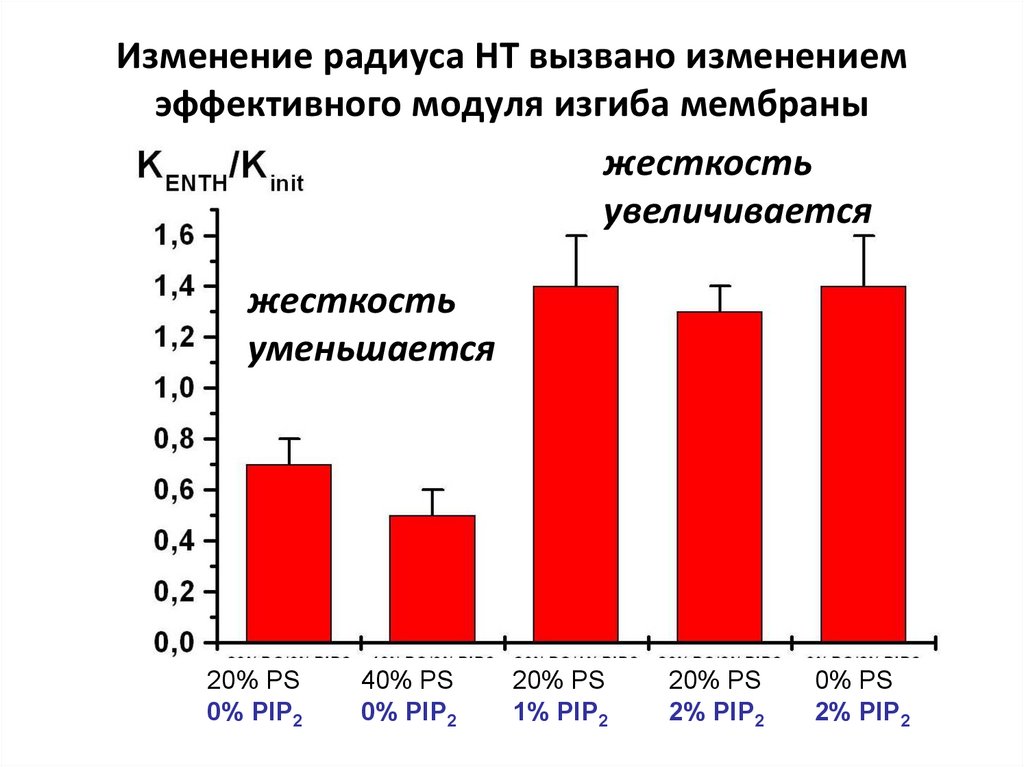
30. Изменение радиуса НТ вызвано изменением эффективного модуля изгиба мембраны
жесткостьувеличивается
жесткость
уменьшается
20% PS
0% PIP2
40% PS
0% PIP2
20% PS
1% PIP2
20% PS
2% PIP2
0% PS
2% PIP2
31. Уменьшение эффективного модуля изгиба, связано с перераспределением ENTH домена между НТ и БЛМ
K 01
Js =
0.6нм
K 2 k BT
Js увеличивается ->
жёсткость уменьшается
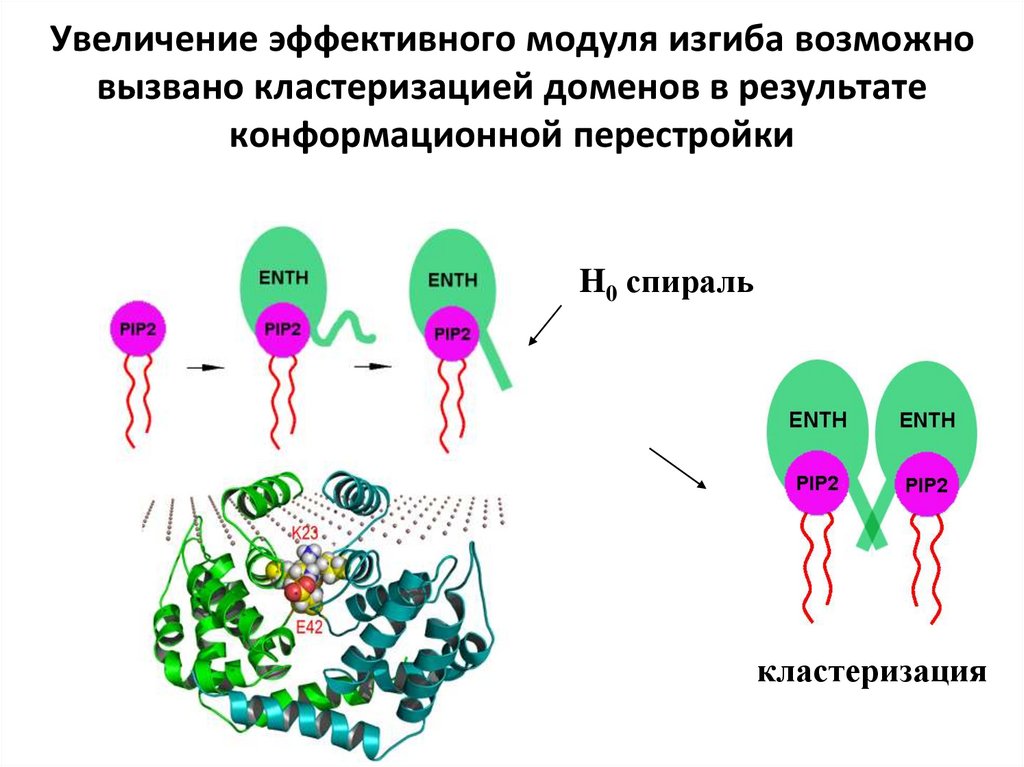
32. Увеличение эффективного модуля изгиба возможно вызвано кластеризацией доменов в результате конформационной перестройки
H0 спиралькластеризация
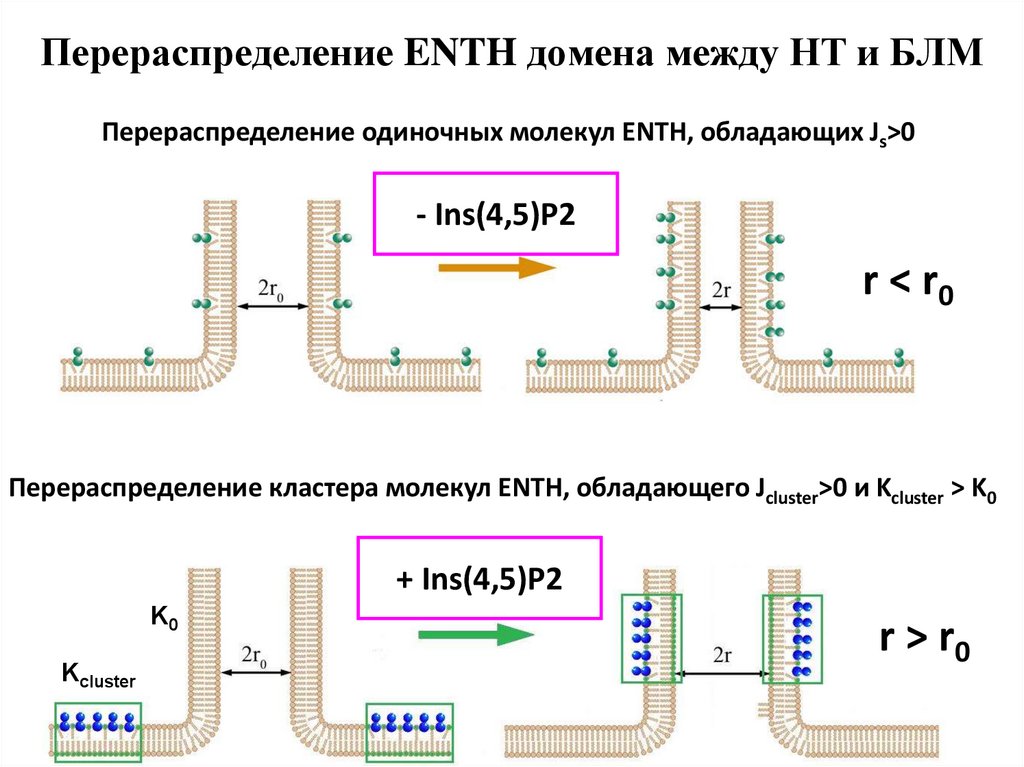
33. Перераспределение ENTH домена между НТ и БЛМ
Перераспределение одиночных молекул ENTH, обладающих Js>0- Ins(4,5)P2
r < r0
Перераспределение кластера молекул ENTH, обладающего Jcluster>0 и Kcluster > K0
+ Ins(4,5)P2
K0
Kcluster
r > r0













 biology
biology








