Устойчивость систем автоматического управления. Основы автоматизации технологических процессов нефтегазового производства

1.

Первое высшее техническое учебное заведение России
Санкт-Петербургский горный университет
императрицы Екатерины II
Основы автоматизации
технологических процессов
нефтегазового производства
Лекция 6
Устойчивость систем автоматического управления
НИКИТИНА Л.Н., к.т.н., доцент кафедры АТПП
г. Санкт-Петербург
2024
1|14

2. Устойчивость САУ

Устойчивость системы автоматического управления является одним из
основных условий ее работоспособности и включает требование
затухания во времени переходных процессов.
2|14

3. Устойчивость САУ

Система является устойчивой, если при ограниченном входном сигнале
её выходной сигнал также является ограниченным.
Если система устойчива, то она противостоит внешним воздействиям, а
выведенная из состояния равновесия возвращается снова к нему.
Система с расходящимся переходным процессом будет неустойчивой и
неработоспособной.
3|14

4. Устойчивость САУ

Необходимое и достаточное условие устойчивости заключается в том,
чтобы все корни характеристического уравнения (полюсы передаточной
функции системы) имели отрицательные вещественные части.
K ( p) bm p m bm 1 p m 1 ... b0 y ( p)
W ( p)
n
n 1
D( p) an p an 1 p ... a0 x( p)
Характеристическое уравнение
4|14

5. Устойчивость САУ

Собственный оператор -
Входной оператор -
D( p ) an p n an 1 p n 1 ... a0
K ( p ) bm p m bm 1 p m 1 ... b0
Полюсами являются корни собственного оператора.
Нулями являются корни входного оператора.
5|14

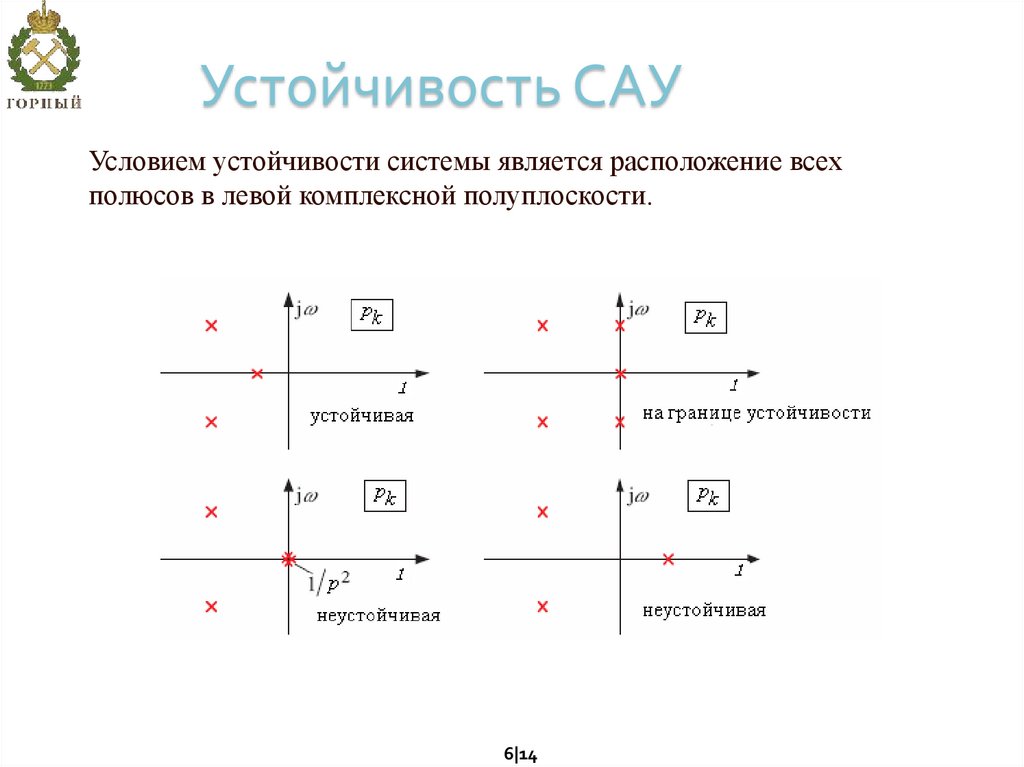
6. Устойчивость САУ

Условием устойчивости системы является расположение всех
полюсов в левой комплексной полуплоскости.
6|14

7. Устойчивость САУ

Устойчивость это свойство системы возвращаться в исходное
состояние равновесия после прекращения воздействия, выведшего
систему состояния первоначального равновесия.
Устойчивость линейной системы определяется не характером
возмущения, а структурой самой системы.
7|14

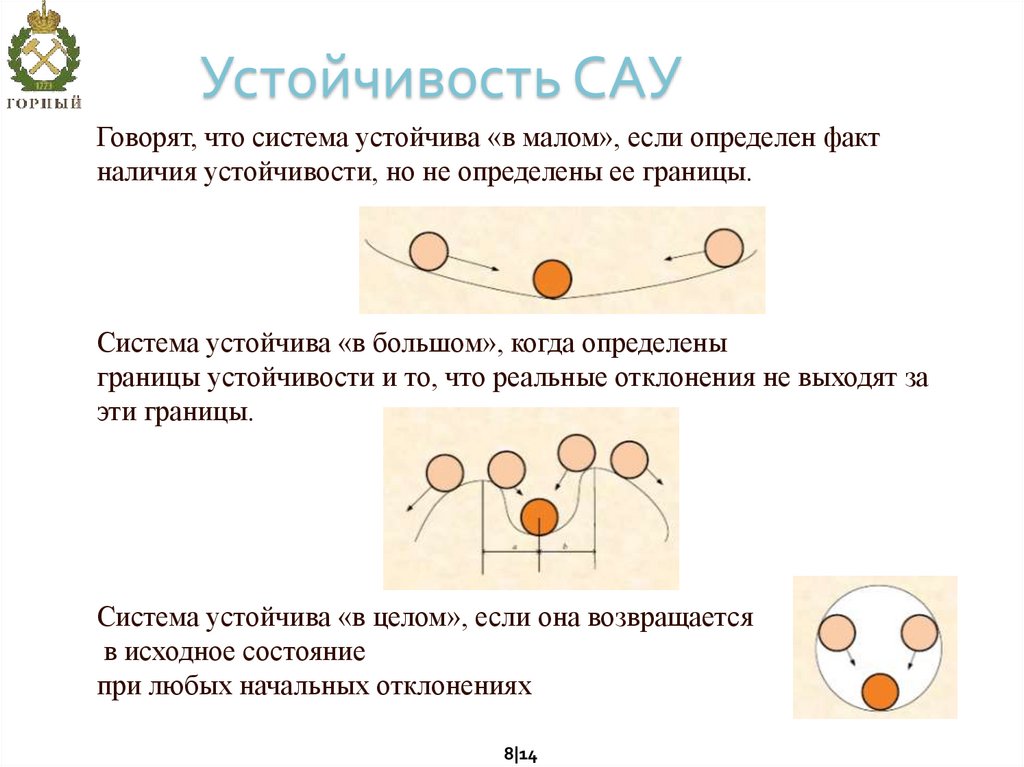
8. Устойчивость САУ

Говорят, что система устойчива «в малом», если определен факт
наличия устойчивости, но не определены ее границы.
Система устойчива «в большом», когда определены
границы устойчивости и то, что реальные отклонения не выходят за
эти границы.
Система устойчива «в целом», если она возвращается
в исходное состояние
при любых начальных отклонениях
8|14

9. Устойчивость САУ

Критериями устойчивости называют определенные правила, по
которым в теории автоматического управления определяют знаки
корней характеристического уравнения, не решая его.
Различают критерии устойчивости:
алгебраические (основаны на составлении по данному
характеристическому уравнению по определенным правилам
алгебраических выражений, по которым можно судить об
устойчивости САУ)
частотные (основаны на исследовании частотных характеристик)
9|14

10. Критерий Гурвица

Критерий Гурвица является алгебраическим критерием и применяется
к коэффициентам характеристического уравнения замкнутой системы.
a0 p a1 p
n
n 1
... an 1 p an 0
Из коэффициентов характеристического уравнения составляют матрицу
по правилу:
1. По диагонали записываются коэффициенты от a1 до an в порядке
возрастания индекса.
2. Дополняют столбцы определителя вверх от диагонали с
последовательно возрастающими, вниз – с последовательно
убывающими индексами.
3. В случае отсутствия индекса, а также, если он меньше 0 или больше
n, на его место пишется 0.
10|14

11. Критерий Гурвица

.
Чтобы система была устойчивой, необходимо и достаточно, чтобы
при a0 >0 были положительными все n определителей, получаемых
из матрицы Гурвица.
11|14

12. Критерий Михайлова

Критерий Михайлова построен на анализе прохождения годографа
характеристического полинома замкнутой системы в комплексной
плоскости при изменении частоты в диапазоне
0
Замкнутая система будет устойчива, если годограф
характеристического уравнения замкнутой системы
при изменении частоты в диапазоне
обходит в положительном направлении n
квадрантов комплексной плоскости,
не пересекаясь нигде сам с собой и
не обращаясь в нуль.
n - порядок характеристического
уравнения
12|14

13. Критерий Найквиста

Критерий Найквиста использует амплитудно-фазовую частотную
характеристику разомкнутой системы, которая может быть получено
либо экспериментально, либо аналитически из передаточной
функции разомкнутой системы заменой p на jω
Если разомкнутая система устойчива, то для устойчивости её в
замкнутом состоянии необходимо и достаточно, чтобы АФЧХ
разомкнутой системы не охватывала критическую точку с
координатами [-1; j0] при изменении частоты в диапазоне 0
13|14

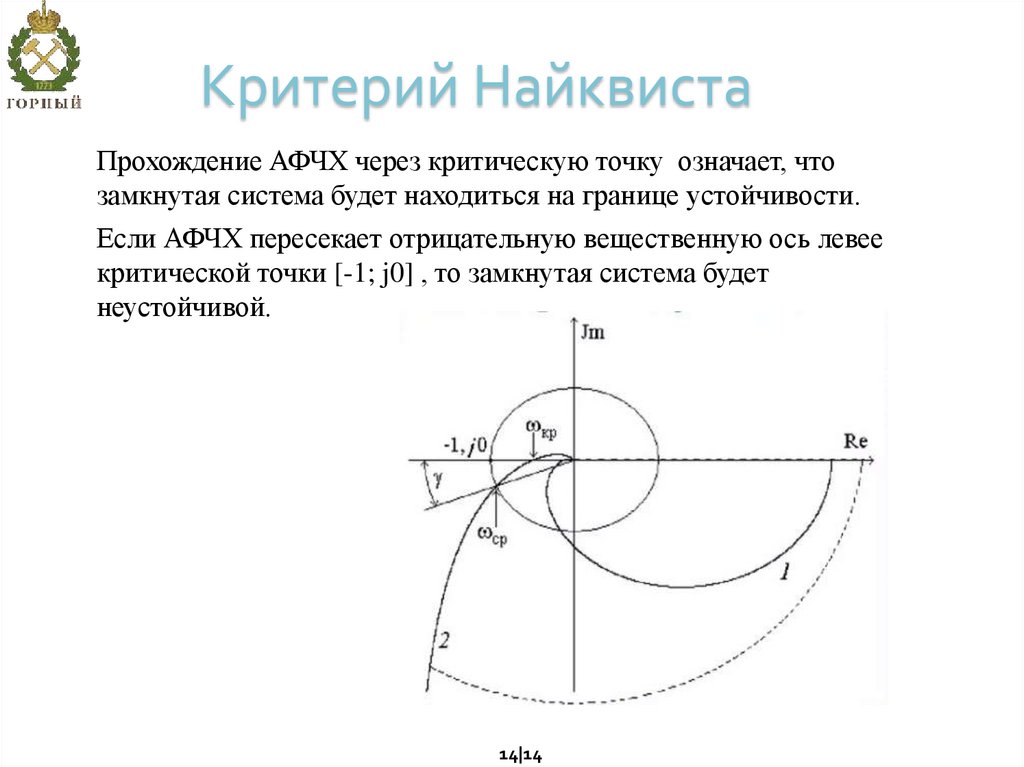
14. Критерий Найквиста

Прохождение АФЧХ через критическую точку означает, что
замкнутая система будет находиться на границе устойчивости.
Если АФЧХ пересекает отрицательную вещественную ось левее
критической точки [-1; j0] , то замкнутая система будет
неустойчивой.
14|14