Similar presentations:
Анализ устойчивости линейных непрерывных систем
1. Тема 6. Анализ устойчивости линейных непрерывных систем
1Тема 6.
Анализ устойчивости линейных
непрерывных систем
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
2.
2Обсуждаемые вопросы
1.
2.
3.
4.
Состояние равновесия динамической
системы
Понятие устойчивости состояния
равновесия
Условие устойчивости
Критерии устойчивости линейных
систем
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
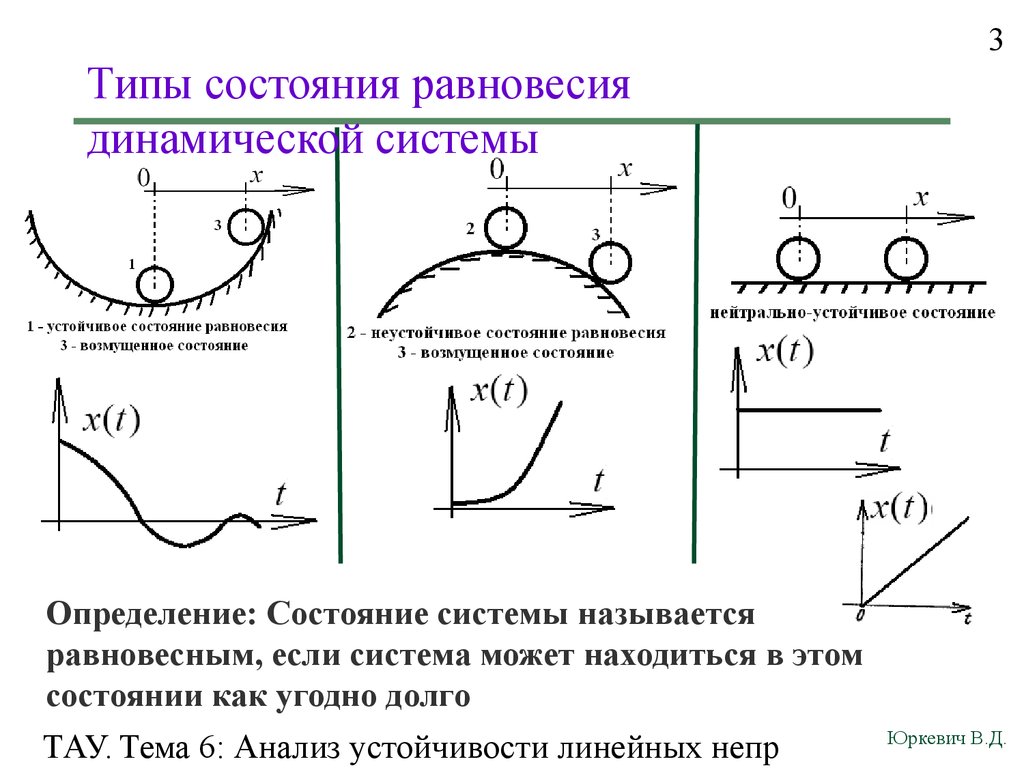
3. Типы состояния равновесия динамической системы
3Определение: Состояние системы называется
равновесным, если система может находиться в этом
состоянии как угодно долго
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
4. Состояние равновесия динамической системы
4Состояние равновесия динамической системы
Рассмотрим автономную динамическую
систему, модель которой задана системой
однородных дифференциальных уравнений
называется точкой равновесия (состояние
равновесия) динамической системы, если
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
5. Состояние равновесия динамического звена
5Состояние равновесия динамического звена
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
6. Состояние равновесия для уравнений в пространстве состояний ОУ
ТАУ. Тема 6: Анализ устойчивости линейных непр6
Юркевич В.Д.
7. Замечание 1
7Замечание 1
Если
1. Состояние равновесия динамической системы является
единственным
2. Состояние равновесия динамической системы является
устойчивым
Тогда данная система называется устойчивой
динамической системой
Замечание 2
Свойство устойчивости состояния равновесия линейной
динамической системы зависит от распределения
корней характеристического полинома этой системы на
комплексной плоскости
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
8. Условие устойчивости линейной системы
8Условие устойчивости линейной системы
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
9. Условие устойчивости линейной системы
9Условие устойчивости линейной системы
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
10.
10ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
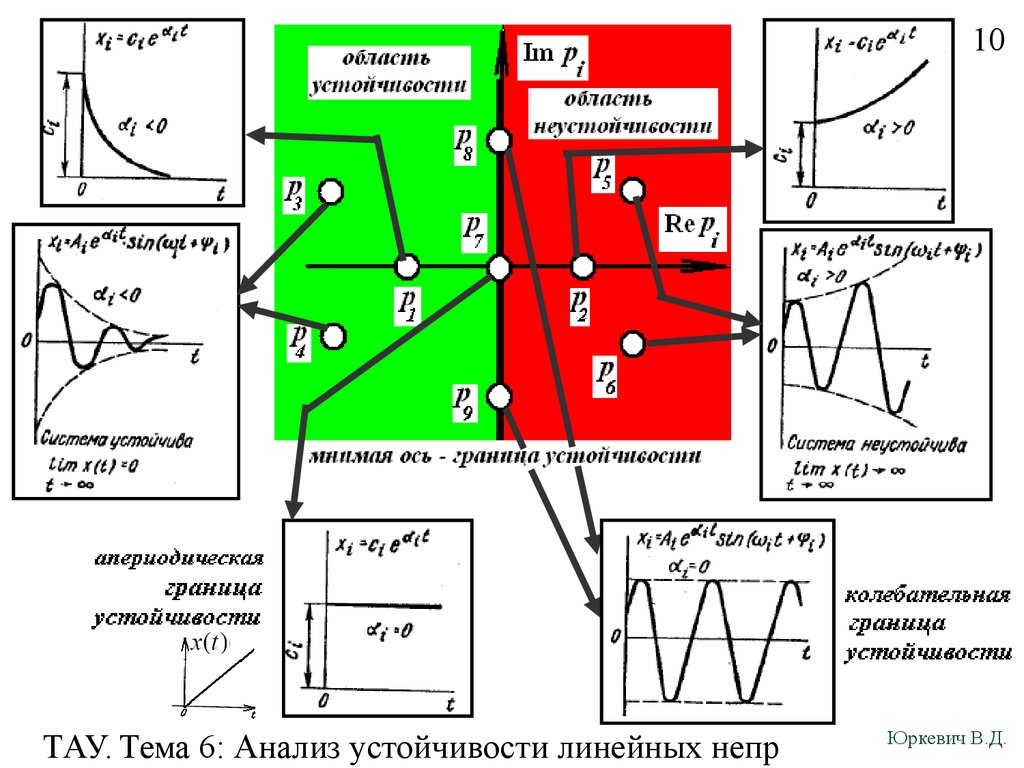
11. Граница устойчивости линейной системы
11Граница устойчивости линейной системы
Для нейтральной системы выделяют два случая:
1. Апериодическая граница устойчивости
2. Колебательная граница устойчивости
Определение: Система находится на апериодической
границе устойчивости, если характеристический
полином имеет нулевой корень, а все остальные корни
имеют строго отрицательную вещественную часть.
Определение: Система находится на колебательной
границе устойчивости, если характеристический
полином имеет пару чисто мнимых комплексносопряженных корней, а все остальные корни имеют строго
отрицательную вещественную часть.
Юркевич В.Д.
ТАУ. Тема 6: Анализ устойчивости линейных непр
12. Критерии устойчивости линейной системы
12Критерии устойчивости линейной системы
Способы проверки устойчивости линейной системы
Прямой способ – путем
вычисления корней
характеристического
полинома
Косвенный способ – с
помощью критериев
устойчивости
Критерий устойчивости – правило проверки устойчивости
системы без вычисления корней характеристического
полинома.
Критерии устойчивости:
1. Алгебраические критерии (например, критерий Гурвица)
2. Частотные критерии (например, критерий Михайлова,
критерий Найквиста)
Юркевич В.Д.
ТАУ. Тема 6: Анализ устойчивости линейных непр
13. Необходимое условие устойчивости
13Необходимое условие устойчивости
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
14. Матрица Гурвица (Hurwitz)
14Матрица Гурвица (Hurwitz)
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
15. Критерий устойчивости Гурвица (Hurwitz)
15Критерий устойчивости Гурвица (Hurwitz)
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
16.
Условие устойчивости системы 1-го порядка16
Условие устойчивости системы 2-го порядка
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
17. Пример 3. Система 3-го порядка
Условие устойчивости системы 3-го порядка17
Пример 3. Система 3-го порядка
Для устойчивости системы 3-го порядка необходимо и
достаточно, чтобы все коэффициенты характеристического
полинома были положительные и произведение средних
коэффициентов было больше чем произведение крайних
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
18. Замечание: Матрица Гурвица (Hurwitz)
18Замечание: Матрица Гурвица (Hurwitz)
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
19. Замечание: Система 3-го порядка
Условие устойчивости системы 3-го порядка19
Замечание: Система 3-го порядка
Для устойчивости системы 3-го порядка необходимо и
достаточно, чтобы все коэффициенты характеристического
полинома были положительные и произведение средних
коэффициентов было больше чем произведение крайних
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
20. Критерий устойчивости Михайлова
20Критерий устойчивости Михайлова
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
21. Годограф Михайлова
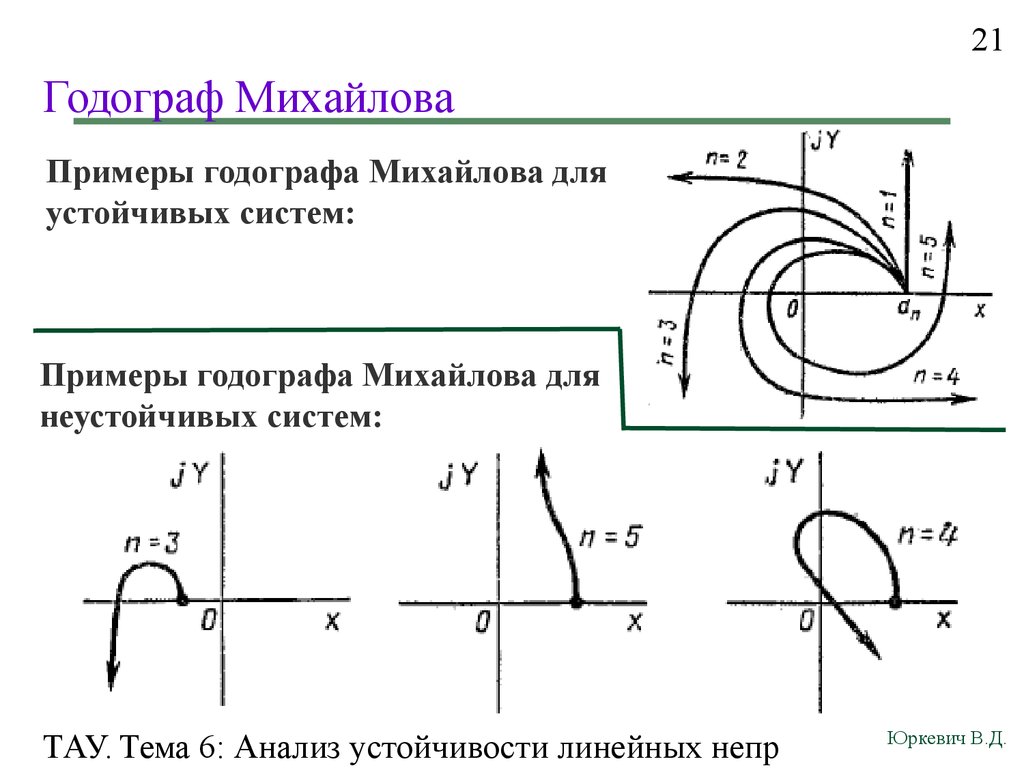
21Годограф Михайлова
Примеры годографа Михайлова для
устойчивых систем:
Примеры годографа Михайлова для
неустойчивых систем:
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
22. Условие для границы устойчивости системы
22Условие для границы устойчивости системы
Пример годографа Михайлова для системы,
находящейся на апериодической границе
устойчивости:
Пример годографа Михайлова
для системы, находящейся на
колебательной границе
устойчивости:
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
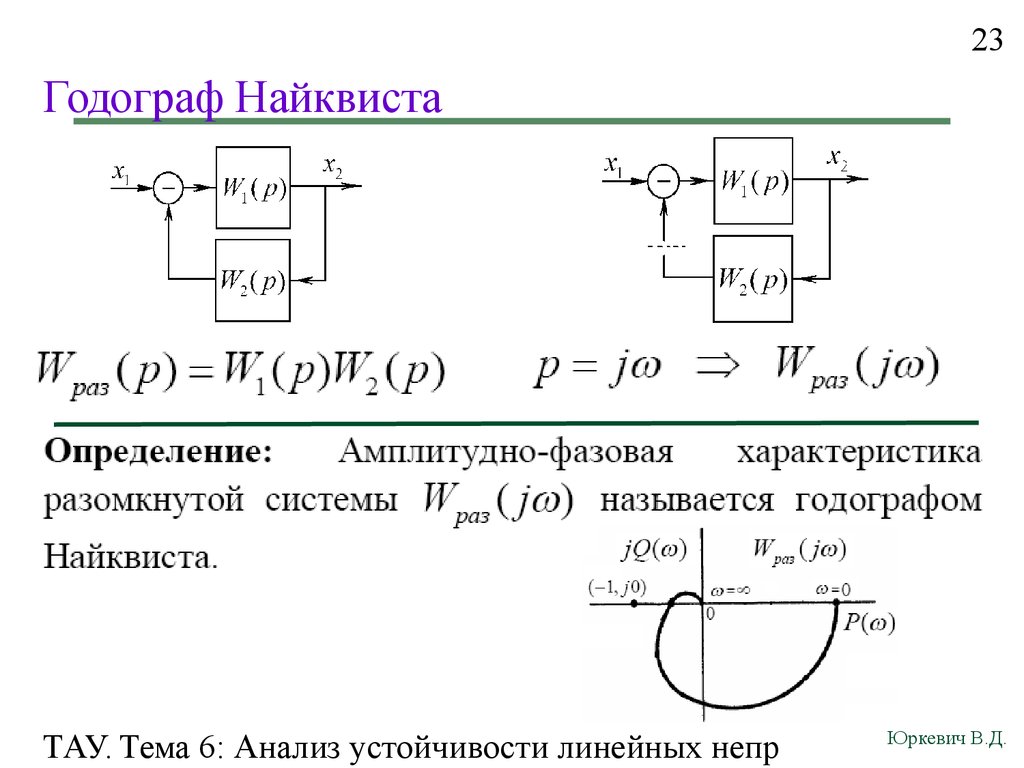
23. Годограф Найквиста
23Годограф Найквиста
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
24. Критерий устойчивости Найквиста (для системы устойчивой в разомкнутом состоянии)
24Примеры годографа Найквиста для случая, когда замкнутая
система является устойчивой
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
25. Критерий устойчивости Найквиста (для системы нейтральной в разомкнутом состоянии)
25-число нулевых корней характеристического полинома
разомкнутой системы
- порядок астатизма замкнутой системы
Примеры годографа Найквиста нейтральных систем для
случая, когда замкнутая система является устойчивой
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
26. Примеры годографа Найквиста для неустойчивых замкнутых систем
ТАУ. Тема 6: Анализ устойчивости линейных непр26
Юркевич В.Д.
27. Условие для границы устойчивости системы
27Условие для границы устойчивости системы
Пример годографа Найквиста для случая, когда замкнутая система
находится на колебательной границе устойчивости
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
28. Логарифмический аналог критерия устойчивости Найквиста (достаточное условие)
ТАУ. Тема 6: Анализ устойчивости линейных непр28
Юркевич В.Д.
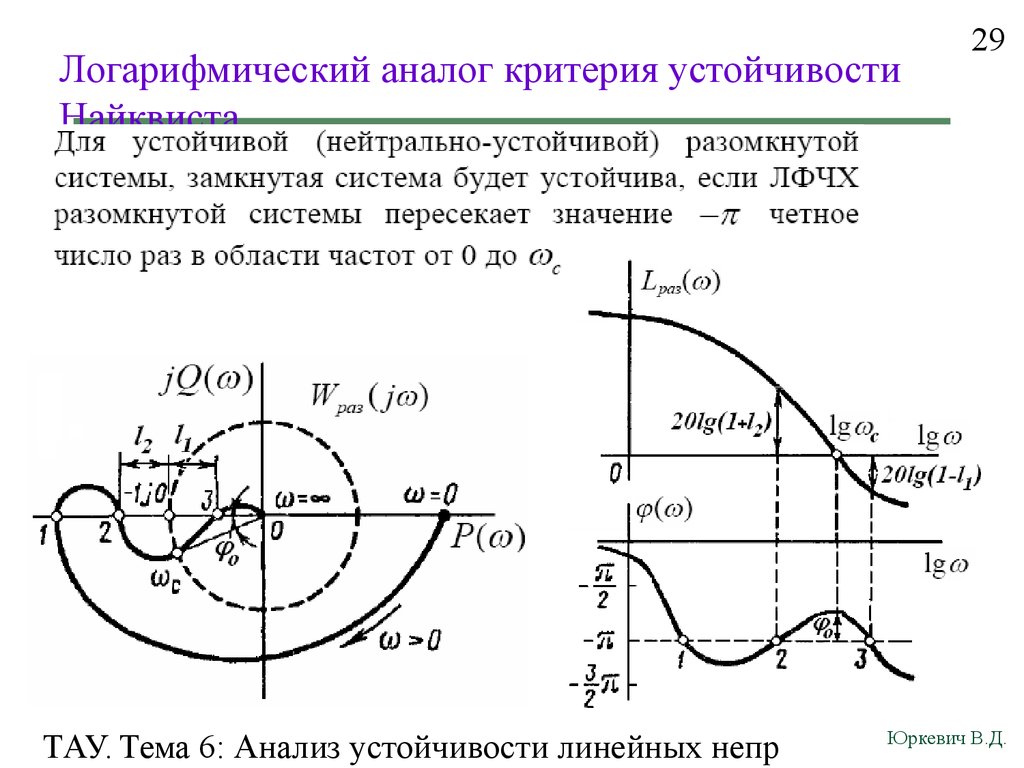
29. Логарифмический аналог критерия устойчивости Найквиста
ТАУ. Тема 6: Анализ устойчивости линейных непр29
Юркевич В.Д.
30. Условие для границы устойчивости системы
30Условие для границы устойчивости системы
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.
31. Тема 7. Область устойчивости, запасы устойчивости
31Тема 7.
Область устойчивости,
запасы устойчивости
ТАУ. Тема 6: Анализ устойчивости линейных непр
Юркевич В.Д.


























 electronics
electronics








