Similar presentations:
Многоугольники. Элементы многоугольника
1.
Многоугольники.Многоугольном называют
фигуру,составленную из
отрезков так,что:
1)смежные отрезки не
лежат на одной прямой
2)несмежные отрезки не
имеют общих точек
Автор:Колесникова Светлана 8а
2.
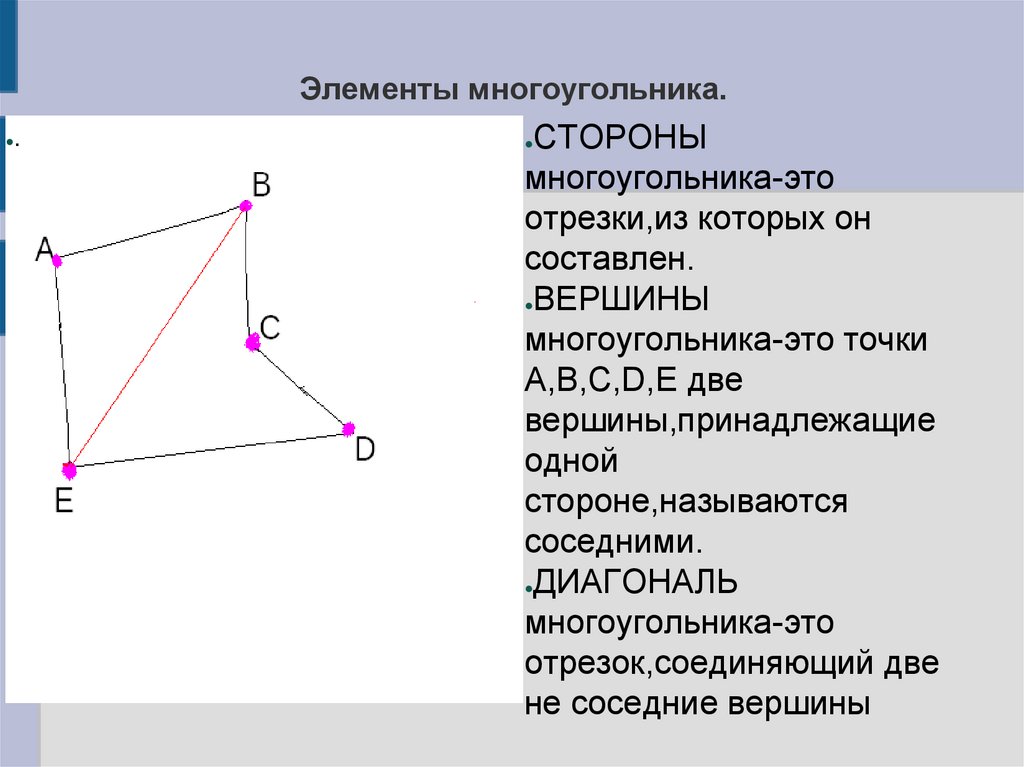
Элементы многоугольника..
СТОРОНЫ
многоугольника-это
отрезки,из которых он
составлен.
●ВЕРШИНЫ
многоугольника-это точки
A,B,C,D,E две
вершины,принадлежащие
одной
стороне,называются
соседними.
●ДИАГОНАЛЬ
многоугольника-это
отрезок,соединяющий две
не соседние вершины
3.
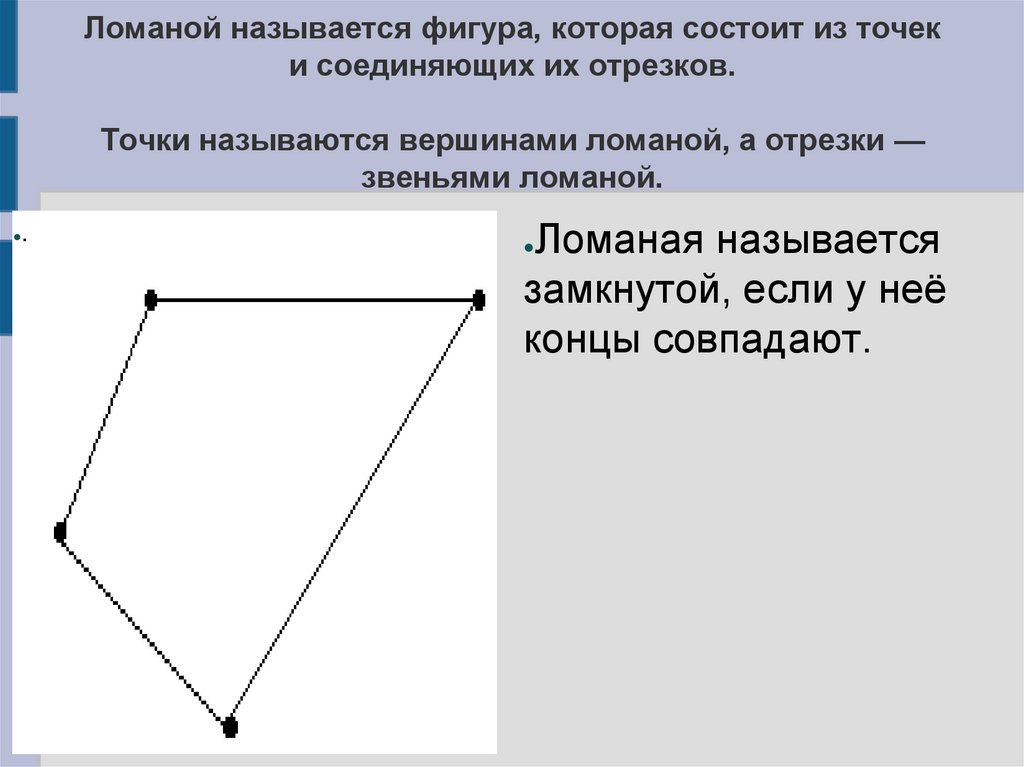
Ломаной называется фигура, которая состоит из точеки соединяющих их отрезков.
Точки называются вершинами ломаной, а отрезки —
звеньями ломаной.
.
Ломаная называется
замкнутой, если у неё
концы совпадают.
4.
.Если концы ломаной
не совпадают, то она
называется
незамкнутой.
5.
.Ломаная называется
простой, если она не
имеет самопересечений.
Обе ломаные которые
были до этого являются
простыми.
На этом рисунке ломаная
с самопересечением.
6.
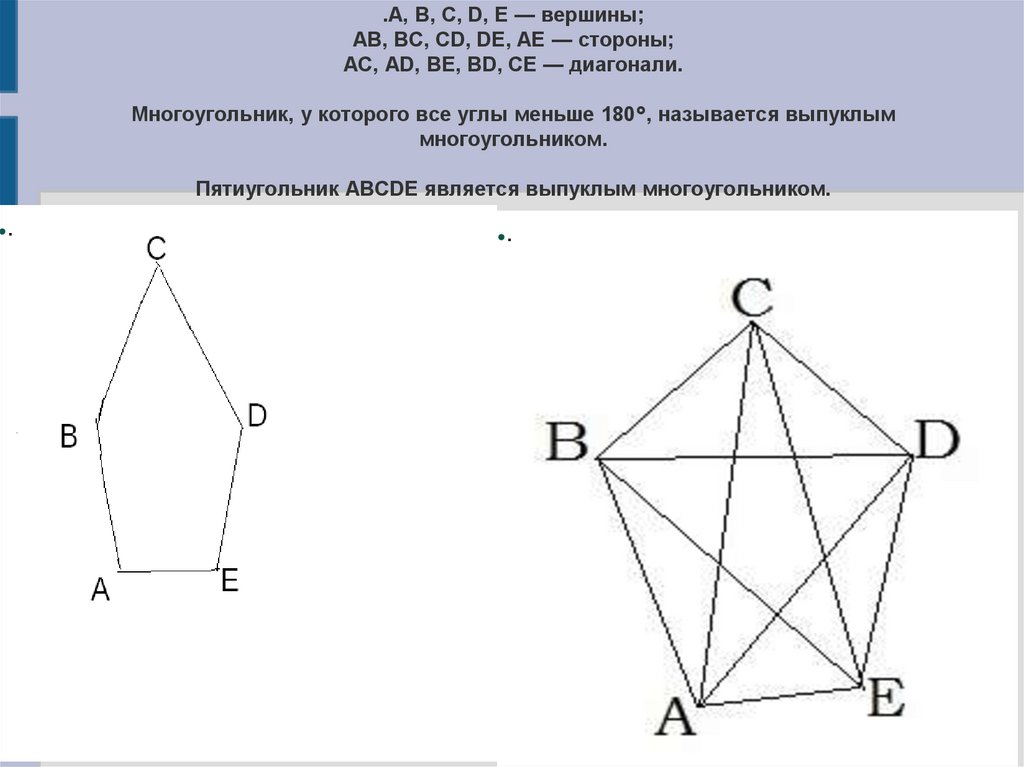
.A, B, C, D, E — вершины;AB, BC, CD, DE, AE — стороны;
AC, AD, BE, BD, CE — диагонали.
Многоугольник, у которого все углы меньше 180°, называется выпуклым
многоугольником.
Пятиугольник ABCDE является выпуклым многоугольником.
.
.
7.
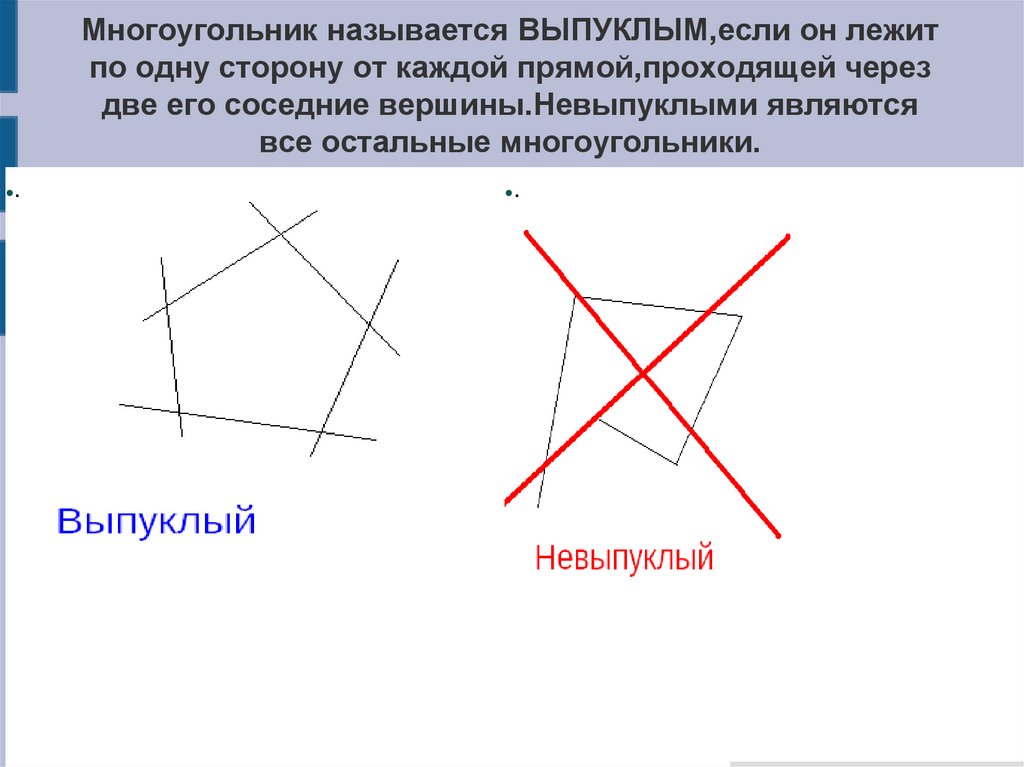
.Многоугольник называется ВЫПУКЛЫМ,если он лежит
по одну сторону от каждой прямой,проходящей через
две его соседние вершины.Невыпуклыми являются
все остальные многоугольники.
●.
8.
Определение : Правильный многоугольник – этовыпуклый многоугольник, у которого все стороны и
углы равны.
Любой многоугольник
●Определение : Периметр
разделяет плоскость на две
многоугольника – сумма
области: внутреннюю и
длин сторон многоугольника.
внешнюю.
● Внутреннюю область также
относят к многоугольнику.
●Многоугольники еще иногда
называют n-угольниками, чтобы
подчеркнуть, что
рассматривается общий случай
наличия какого-то неизвестного
количества углов (n штук).
9.
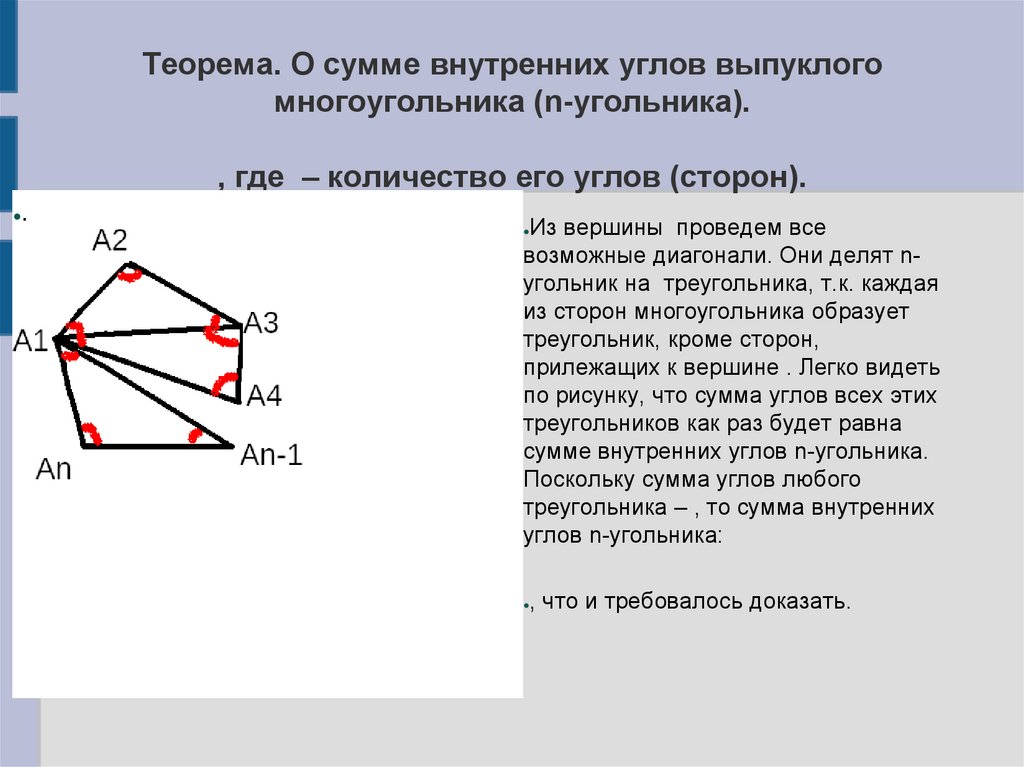
Теорема. О сумме внутренних углов выпуклогомногоугольника (n-угольника).
, где – количество его углов (сторон).
.
Из вершины проведем все
возможные диагонали. Они делят nугольник на треугольника, т.к. каждая
из сторон многоугольника образует
треугольник, кроме сторон,
прилежащих к вершине . Легко видеть
по рисунку, что сумма углов всех этих
треугольников как раз будет равна
сумме внутренних углов n-угольника.
Поскольку сумма углов любого
треугольника – , то сумма внутренних
углов n-угольника:
, что и требовалось доказать.
10.
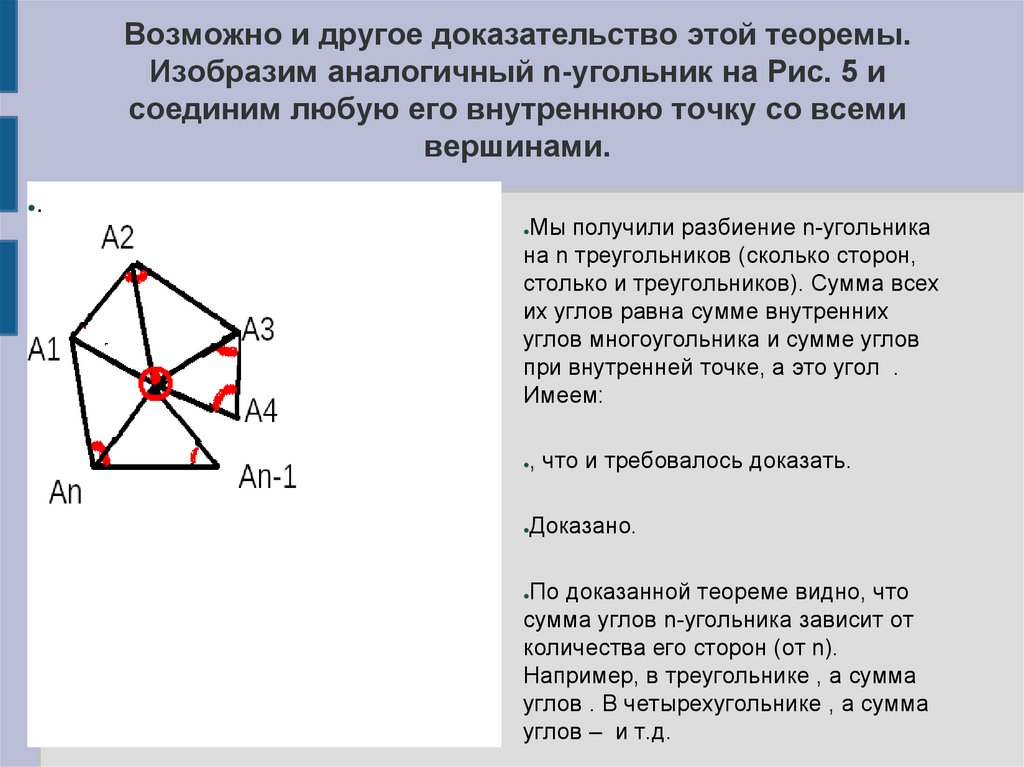
Возможно и другое доказательство этой теоремы.Изобразим аналогичный n-угольник на Рис. 5 и
соединим любую его внутреннюю точку со всеми
вершинами.
.
Мы получили разбиение n-угольника
на n треугольников (сколько сторон,
столько и треугольников). Сумма всех
их углов равна сумме внутренних
углов многоугольника и сумме углов
при внутренней точке, а это угол .
Имеем:
, что и требовалось доказать.
Доказано.
По доказанной теореме видно, что
сумма углов n-угольника зависит от
количества его сторон (от n).
Например, в треугольнике , а сумма
углов . В четырехугольнике , а сумма
углов – и т.д.




 mathematics
mathematics








