Многоугольник, его элементы и его свойства. Распознавание некоторых многоугольников

1.

Многоугольник, его элементы и его
свойства.
Распознавание некоторых
многоугольников.
Выпуклые и невыпуклые многоугольники.
Правильные многоугольники.
1

2.

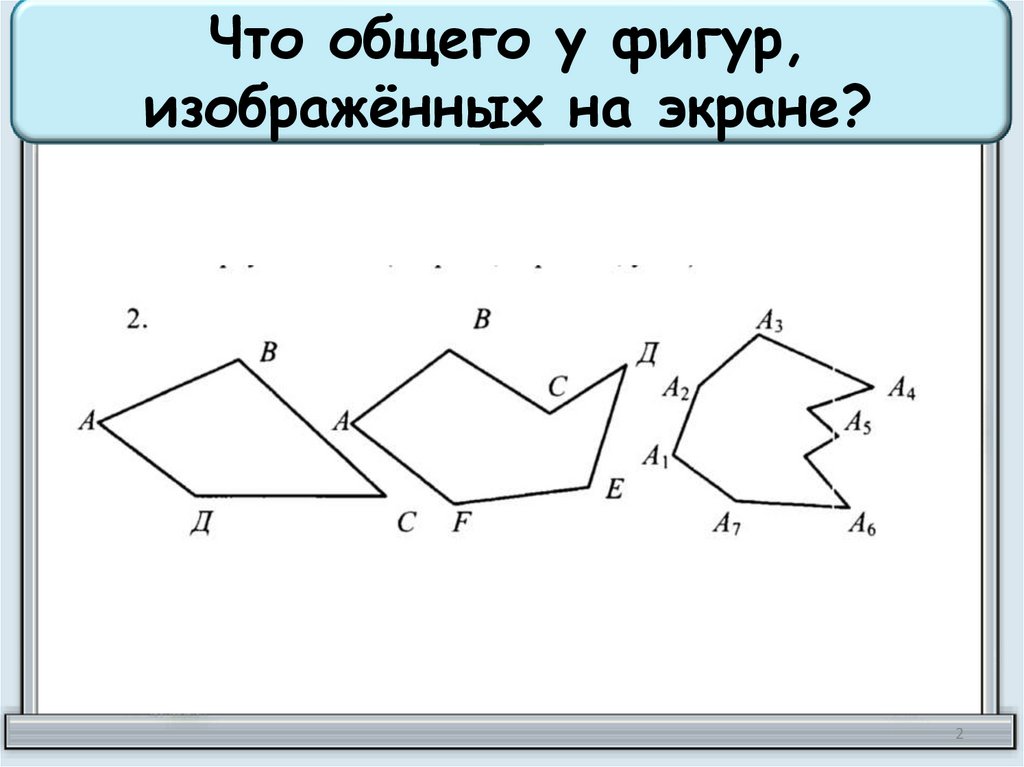
Что общего у фигур,
изображённых на экране?
2

3.

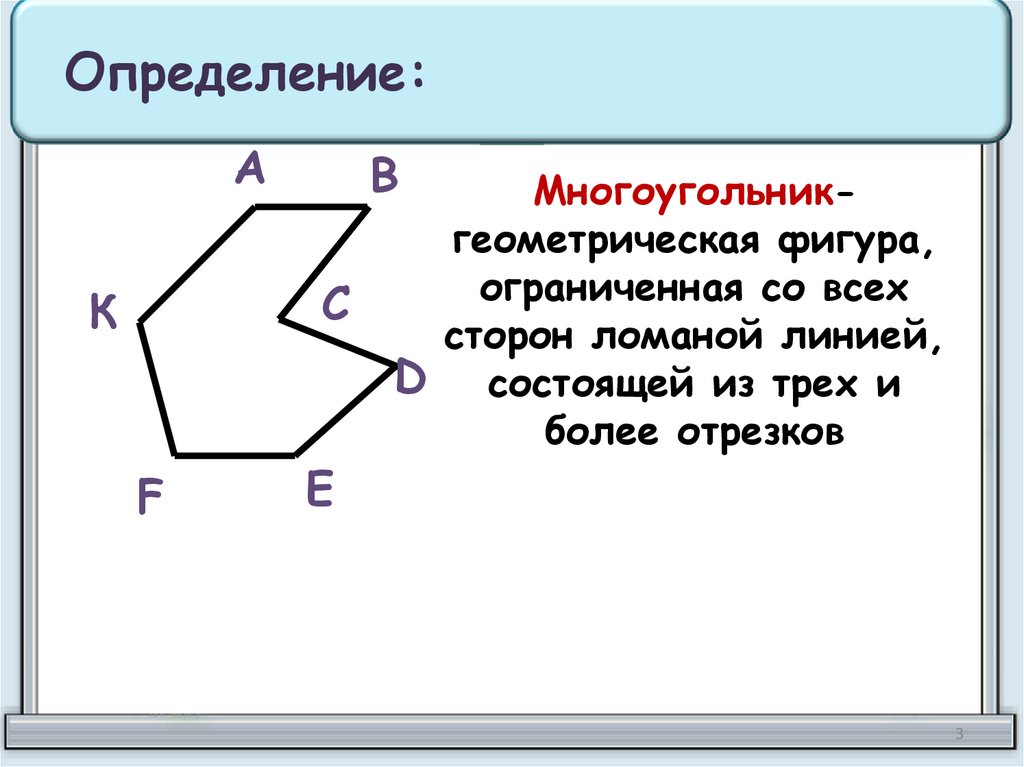
Определение:
А
В
С
К
F
Е
Многоугольникгеометрическая фигура,
ограниченная со всех
сторон ломаной линией,
D состоящей из трех и
более отрезков
3

4.

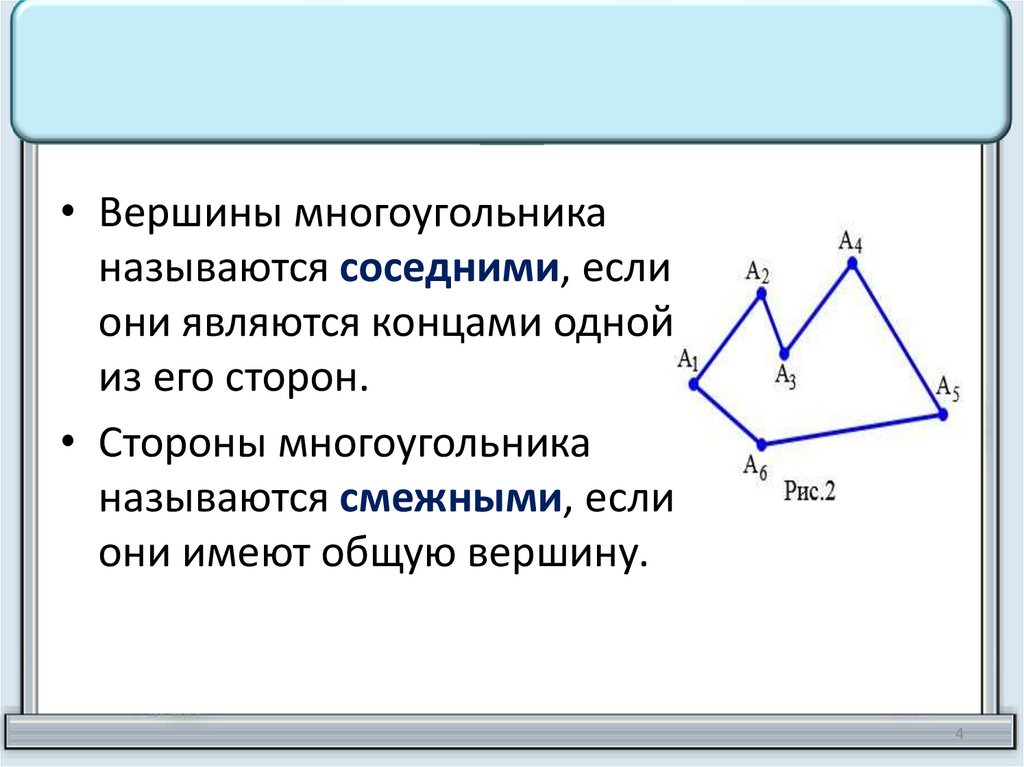
• Вершины многоугольника
называются соседними, если
они являются концами одной
из его сторон.
• Стороны многоугольника
называются смежными, если
они имеют общую вершину.
4

5.

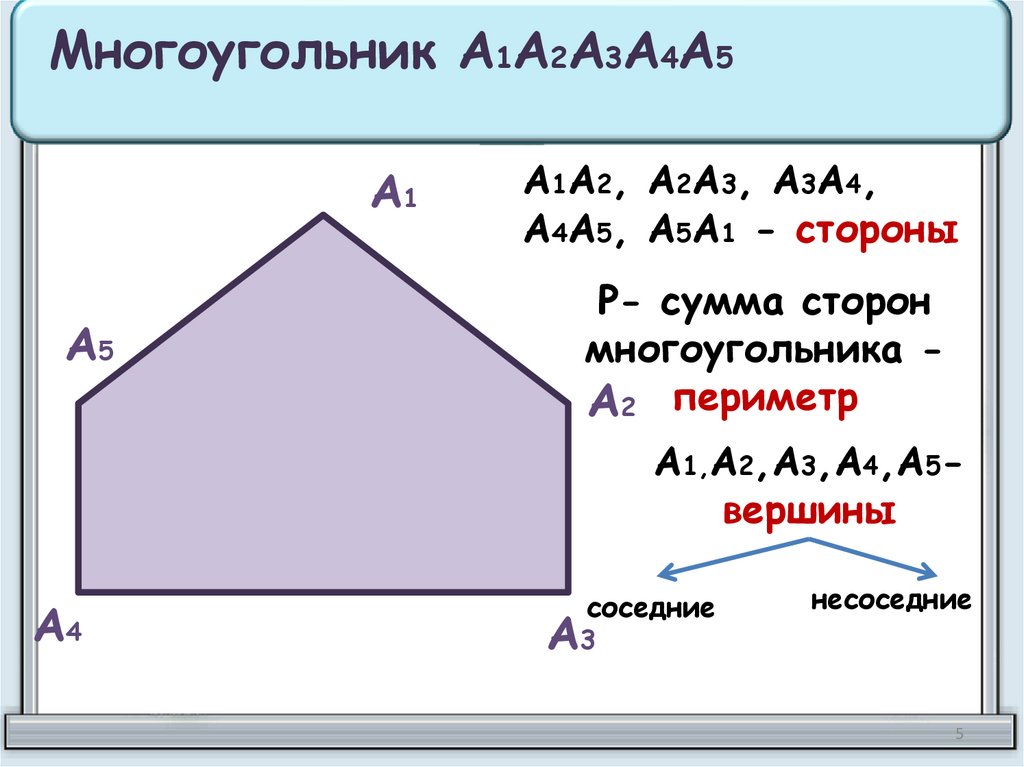
Многоугольник А1А2А3А4А5
А1
А5
А1А2, А2А3, А3А4,
А4А5, А5А1 - стороны
Р- сумма сторон
многоугольника А2 периметр
А1,А2,А3,А4,А5вершины
А4
соседние
А3
несоседние
5

6.

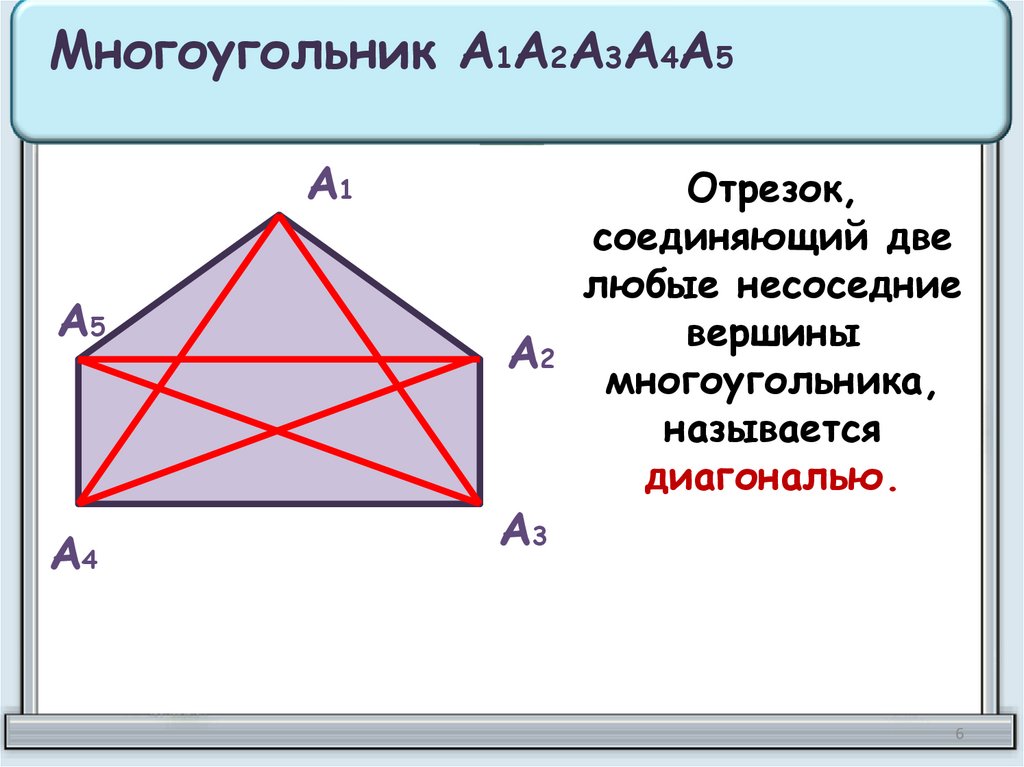
Многоугольник А1А2А3А4А5
А1
А5
А4
А2
А3
Отрезок,
соединяющий две
любые несоседние
вершины
многоугольника,
называется
диагональю.
6

7.

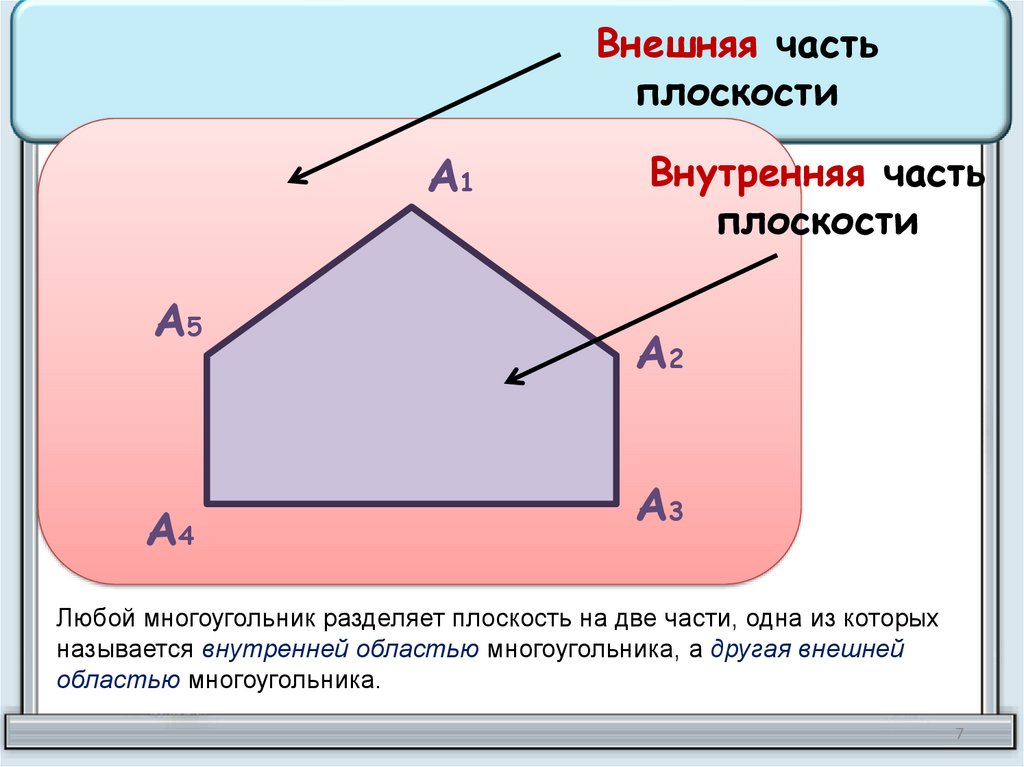
Внешняя часть
плоскости
А1
А5
А4
Внутренняя часть
плоскости
А2
А3
Любой многоугольник разделяет плоскость на две части, одна из которых
называется внутренней областью многоугольника, а другая внешней
областью многоугольника.
7

8.

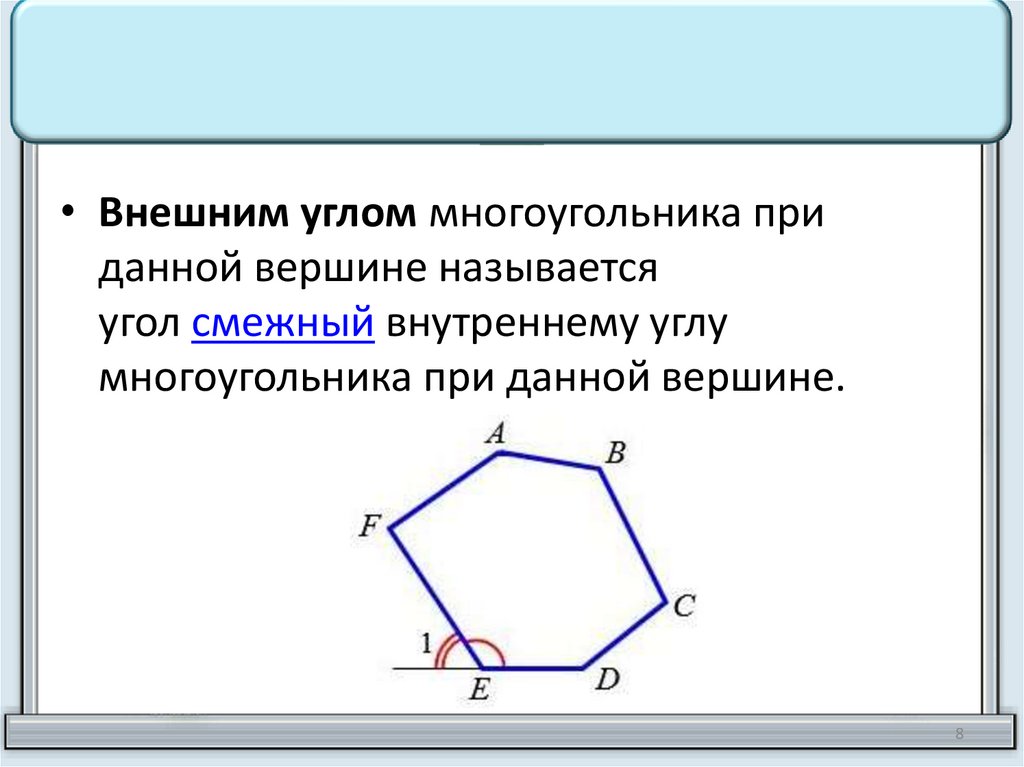
• Внешним углом многоугольника при
данной вершине называется
угол смежный внутреннему углу
многоугольника при данной вершине.
8

9.

• Многоугольник с тремя вершинами
называется треугольником, с четыремя вершинами −
четырехугольником, с пяти вершинами − пятиугольником,
и т.д. Многоугольник с n вершинами
называется n−угольником.
9

10.

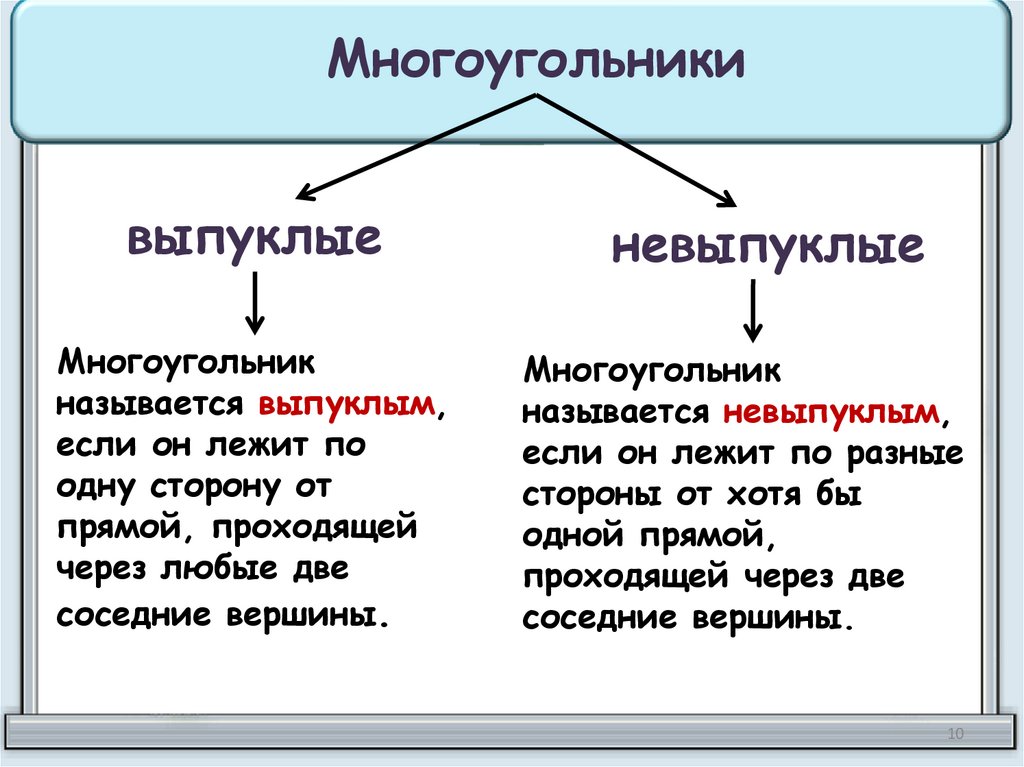
Многоугольники
выпуклые
Многоугольник
называется выпуклым,
если он лежит по
одну сторону от
прямой, проходящей
через любые две
соседние вершины.
невыпуклые
Многоугольник
называется невыпуклым,
если он лежит по разные
стороны от хотя бы
одной прямой,
проходящей через две
соседние вершины.
10

11.

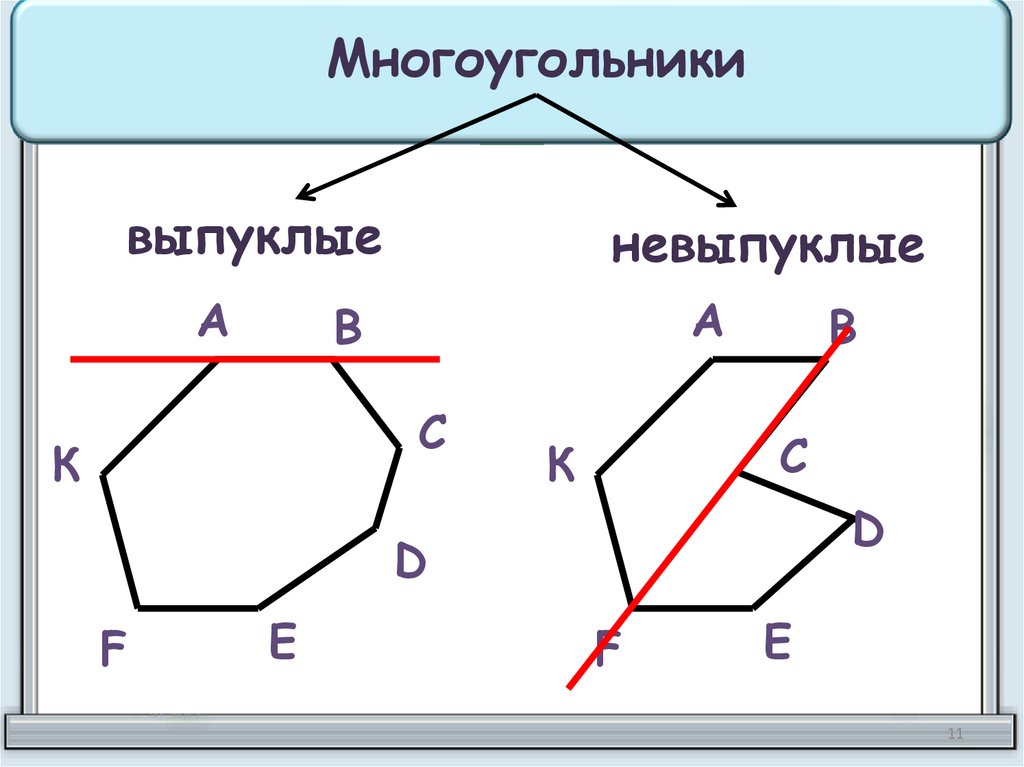
Многоугольники
выпуклые
А
невыпуклые
А
В
С
К
В
С
К
D
D
F
Е
F
Е
11

12.

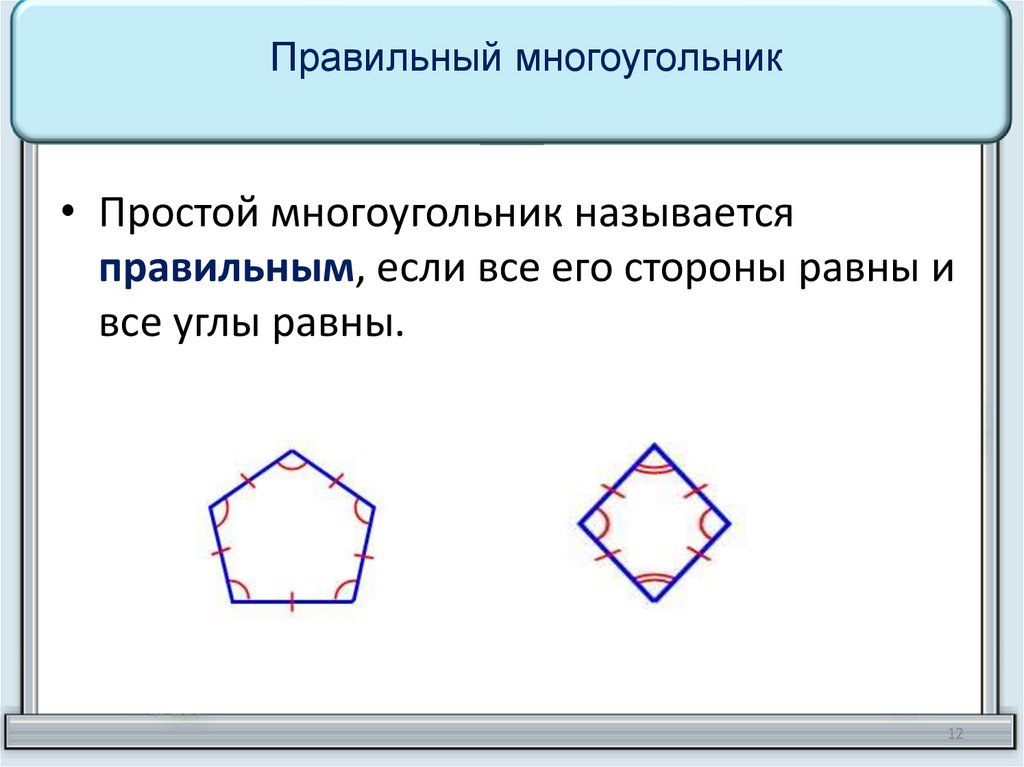
Правильный многоугольник
• Простой многоугольник называется
правильным, если все его стороны равны и
все углы равны.
12

13.

Нарисуйте четырёхугольник, пятиугольник и
шестиугольник.
Проведите в них диагонали, исходящие из
одной вершины.
2
3
4
Сколько треугольников образовалось в каждой
фигуре?
13

14.

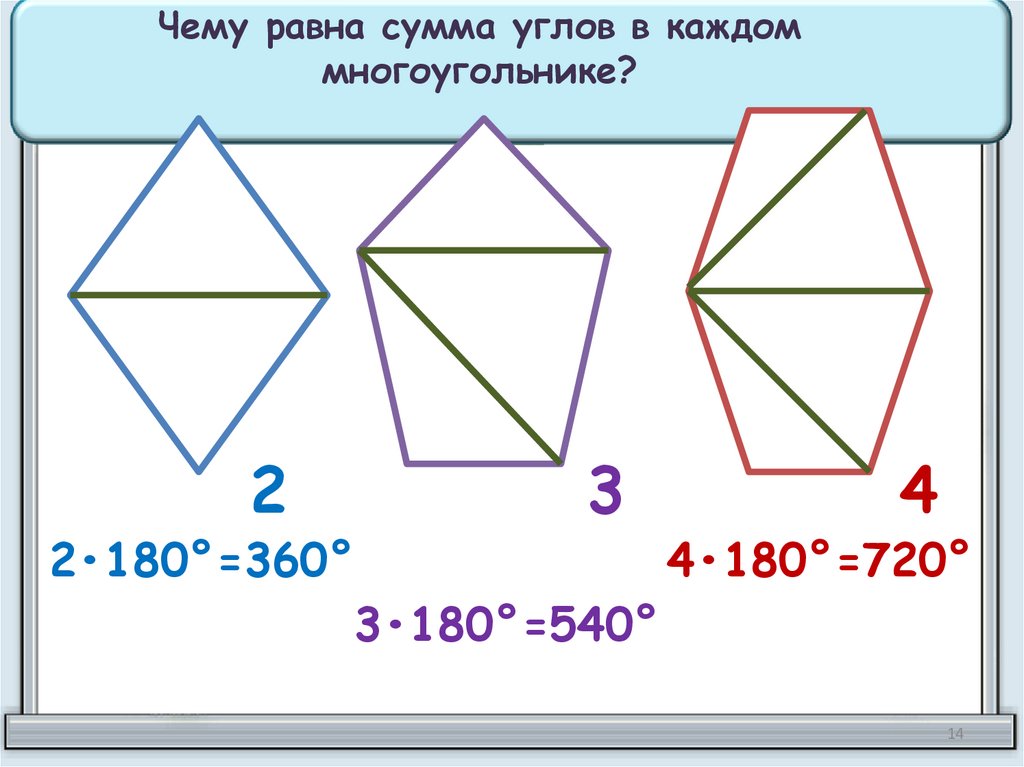
Чему равна сумма углов в каждом
многоугольнике?
2
3
4
2•180°=360°
4•180°=720°
3•180°=540°
14

15.

15