Similar presentations:
Кинематика. Механика
1.
Механика:Кинематика – это раздел механики,
описывает механическое движение тела
(Как движется тело?)
который
Динамика – это раздел механики, который объясняет
характер движения и взаимодействия тел
(Почему именно так движется тело?)
2.
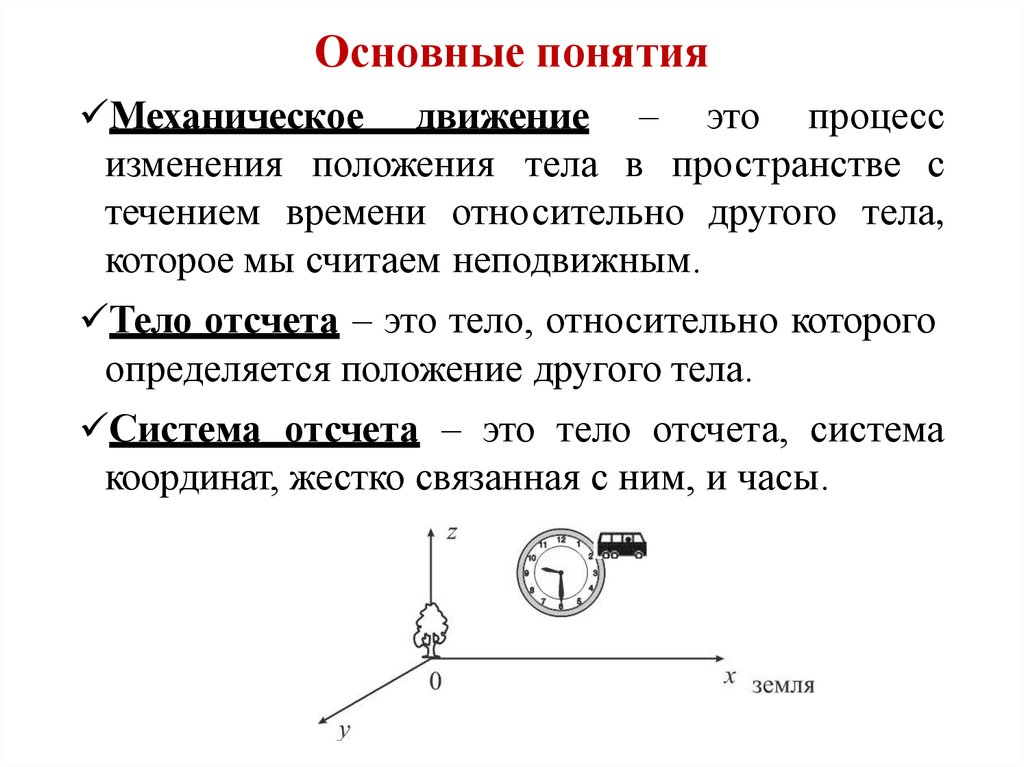
Основные понятияМеханическое движение – это процесс
изменения положения тела в пространстве с
течением времени относительно другого тела,
которое мы считаем неподвижным.
Тело отсчета – это тело, относительно которого
определяется положение другого тела.
Система отсчета – это тело отсчета, система
координат, жестко связанная с ним, и часы.
3.
МоделиМатериальная точка – это тело, размерами и
формой которого можно пренебречь в данной
задаче.
Абсолютно твердое тело – это тело, расстояние
между любыми двумя точками которого остается
постоянным при любых внешних воздействиях.
4.
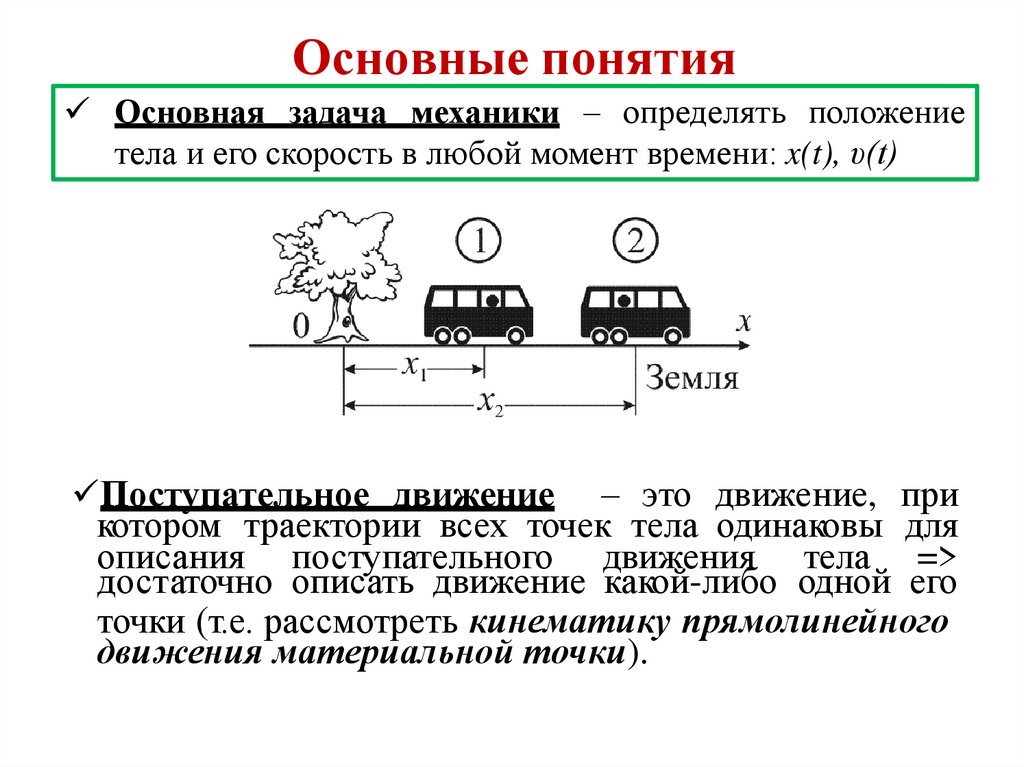
Основные понятияОсновная задача механики – определять положение
тела и его скорость в любой момент времени: x(t), υ(t)
Поступательное движение – это движение, при
котором траектории всех точек тела одинаковы для
описания поступательного движения тела =>
достаточно описать движение какой-либо одной его
точки (т.е. рассмотреть кинематику прямолинейного
движения материальной точки).
5.
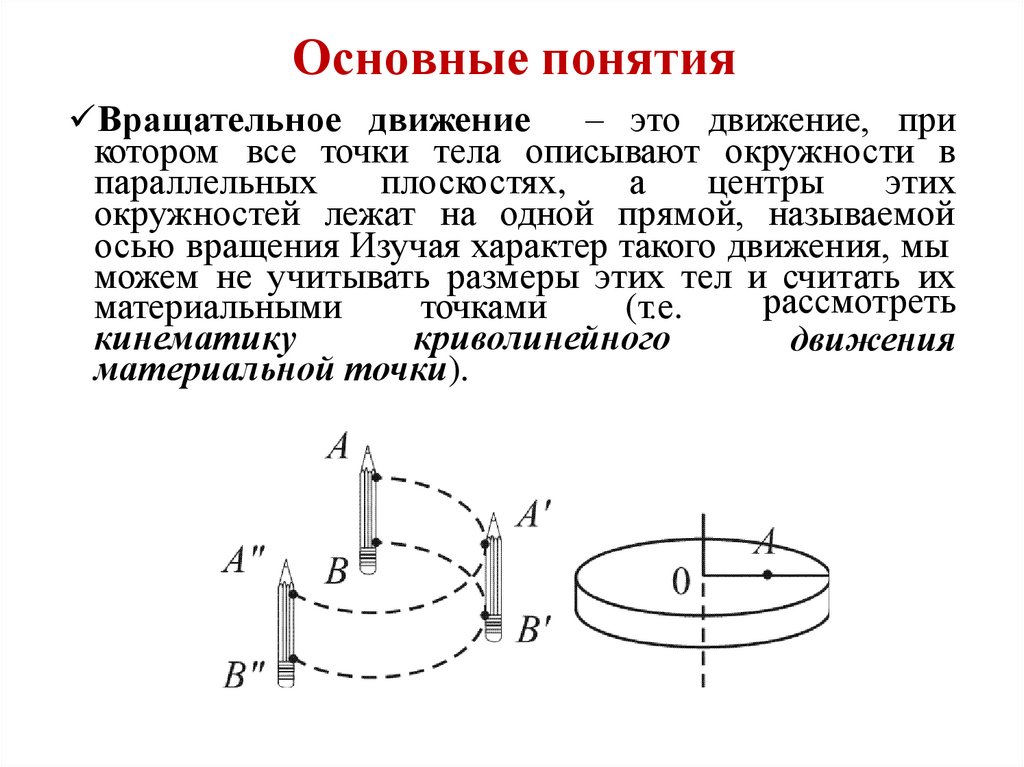
Основные понятияВращательное движение
– это движение, при
котором все точки тела описывают окружности в
параллельных
плоскостях,
а
центры
этих
окружностей лежат на одной прямой, называемой
осью вращения Изучая характер такого движения, мы
можем не учитывать размеры этих тел и считать их
рассмотреть
материальными
точками
(т.е.
кинематику
криволинейного
движения
материальной точки).
6.
Основные понятияВектор – это направленный отрезок прямой
(точка приложения, направление, модуль)
Векторы
Обозначения
Формулы
7.
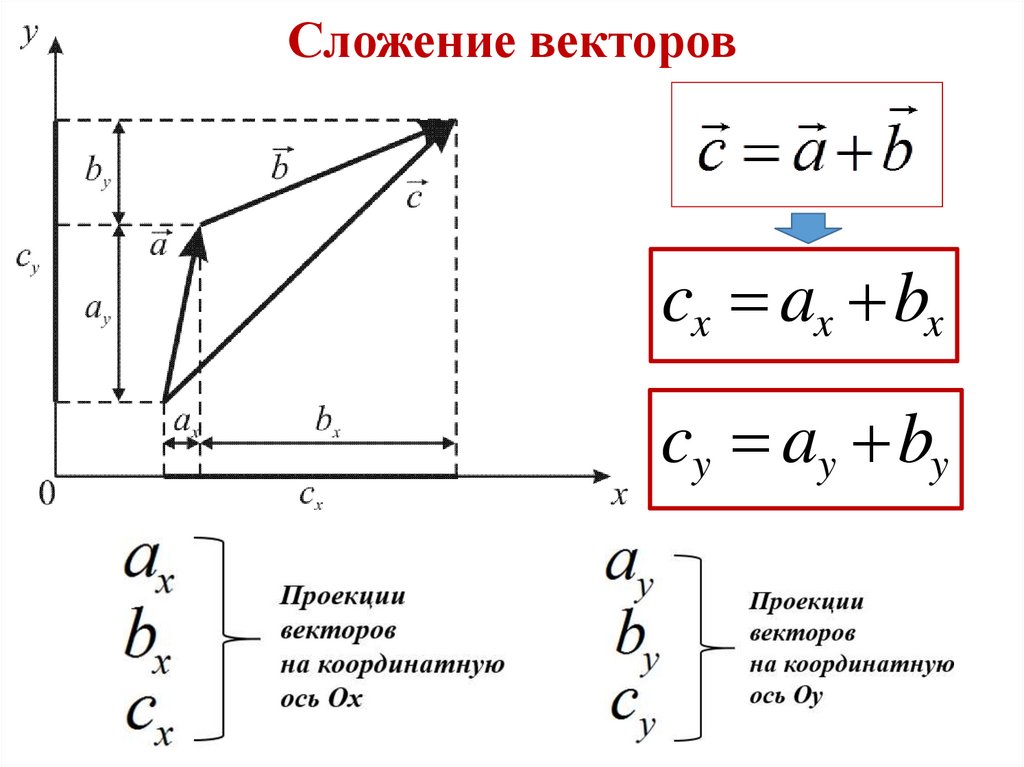
Сложение векторова) правило параллелограмма
б) правило треугольника
8.
Сложение векторовcx ax bx
cy ay by
9.
Основные понятияВекторы
Обозначения
r0 – радиус-вектор точки в начальный
момент времени (t = 0)
r – радиус-вектор точки через время t
Δr(s) – перемещение точки за время t
Δx (sx), Δy (sx) – изменения координат
точки за время t (проекции
перемещения точки на оси OX и OY)
Формулы
r r r
0
s r
s x x x0
s y у у0
s
s2 y2
x
y
10.
Прямолинейное равномерное движениеs
t
s t
x x0
x
t
s x xt
sx x x0
x x0 xt
– закон
равномерного
прямолинейного
движения
11.
Прямолинейное равномерное движениеУравнения
зависимости
от времени
Координата
Скорость
x x0 xt
x const
x 1м
1м / с
Графики
зависимости
от времени
12.
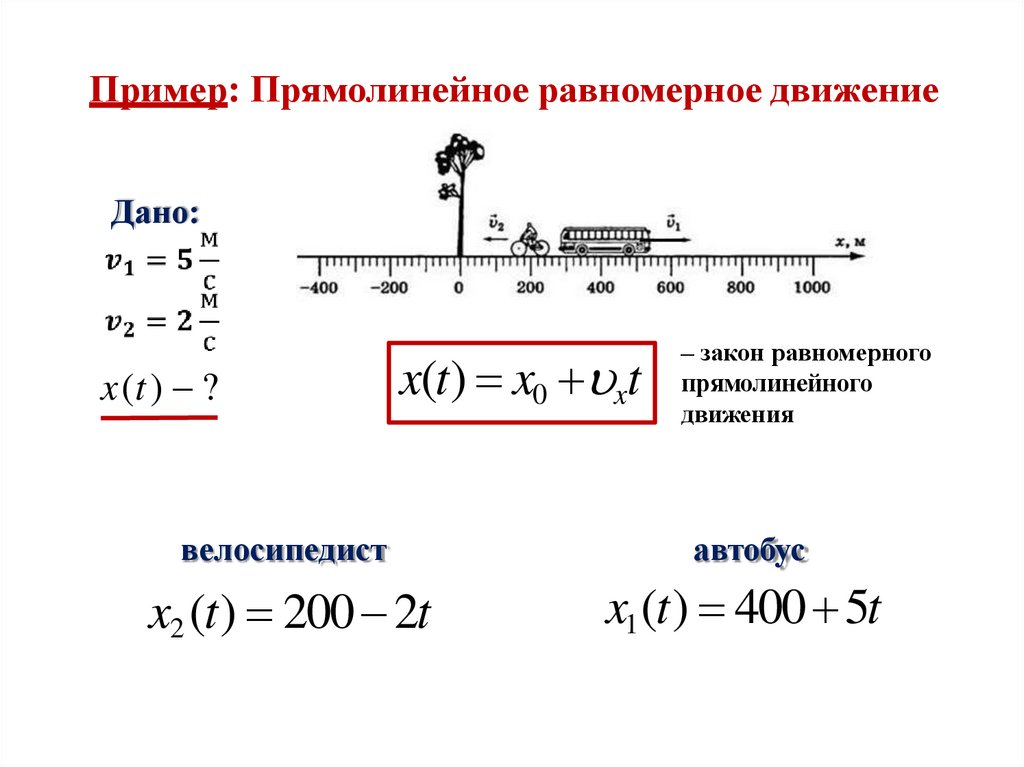
Пример: Прямолинейное равномерное движениеДано:
x(t ) ?
x(t) x0 xt
– закон равномерного
прямолинейного
движения
велосипедист
автобус
x2 (t) 200 2t
x1 (t) 400 5t
13.
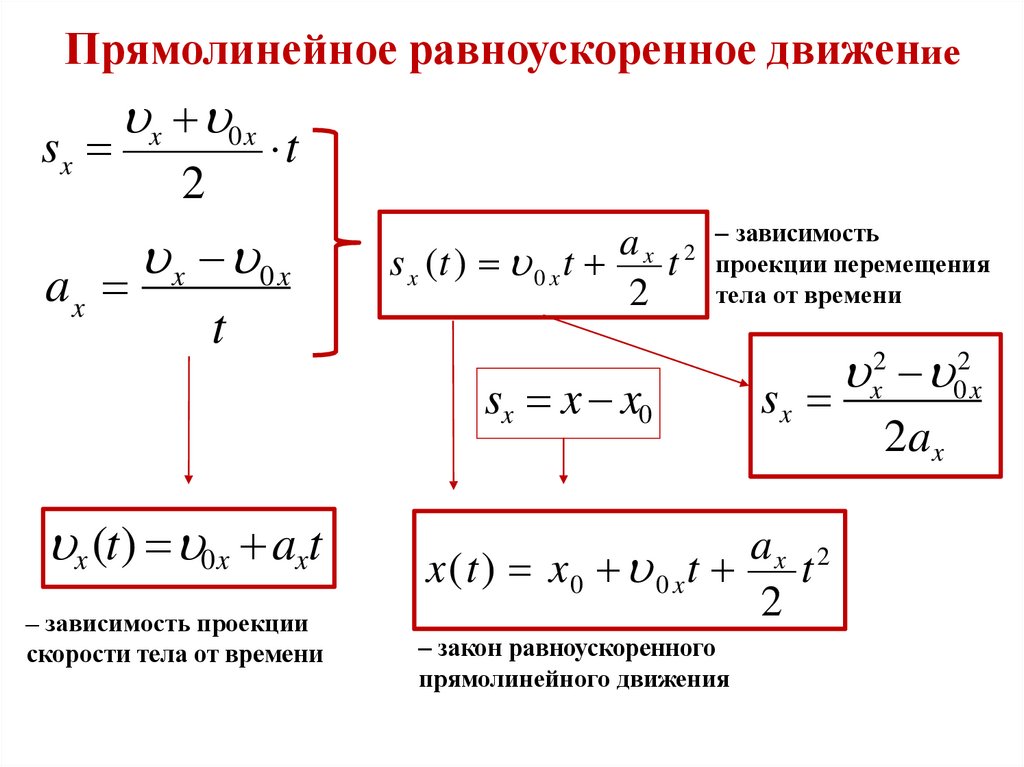
Прямолинейное равноускоренное движениеа 1м / с 2
14.
Прямолинейное равноускоренное движениеДвижение
Равномерное
Равноускоренное
График зависимости
проекции скорости от
времени vx(t)
Формула
для проекции
перемещения
sx xt
x 0 x
s
2
t
15.
Прямолинейное равноускоренное движениеsx
x 0 x
ax
2
t
x 0 x
t
зависимость
a x 2 –проекции
перемещения
s x (t ) 0 x t
t
тела от времени
2
sx x x0
x (t) 0x axt
– зависимость проекции
скорости тела от времени
sx
ax 2
x(t) x 0 0 x t
t
2
– закон равноускоренного
прямолинейного движения
x2 02x
2ax
16.
Прямолинейное равноускоренное движениеt=0
Уравнения зависимости
от времени
x(t) x0 0 x t
ax 2
t
2
Графики зависимости
от времени
Координата
x (t) 0 x a x t
Скорость
a x (t) const
Ускорение
17.
Пример: Прямолинейное равноускоренное движениеДано:
x (t ) ?
ax
s x (t ) ?
x 0x
t
x(t ) ?
8м/ c 2м/ c
м
ax
2 2
с
3c
x (t) 0x axt x (t) 2 2t
ax 2
s x (t) 0 x t t
2
a
x(t) x0 0 x t x t 2
2
s x (t ) 2t t 2
x(t) 600 2t t 2
18.
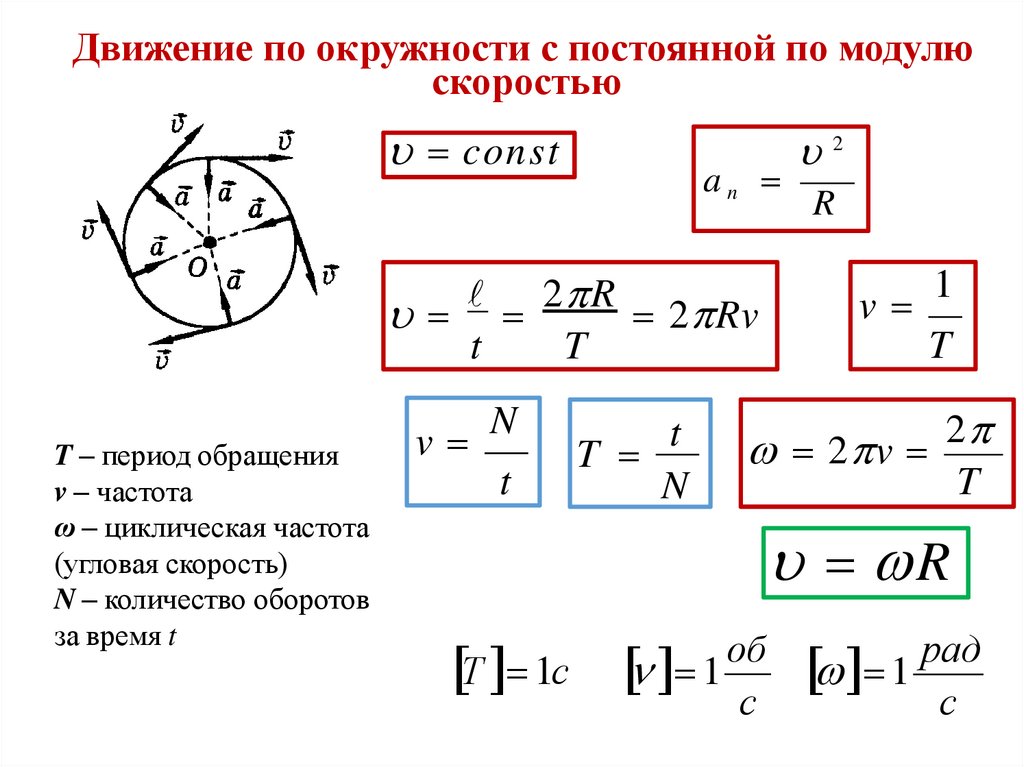
Движение по окружности с постоянной по модулюскоростью
const
an
2 R 2 Rv
t
T
T – период обращения
v – частота
ω – циклическая частота
(угловая скорость)
N – количество оборотов
за время t
v
N
t
t
T
N
2
R
v
1
T
2
2 v
T
R
Т 1с
об
1
с
рад
1
с
19.
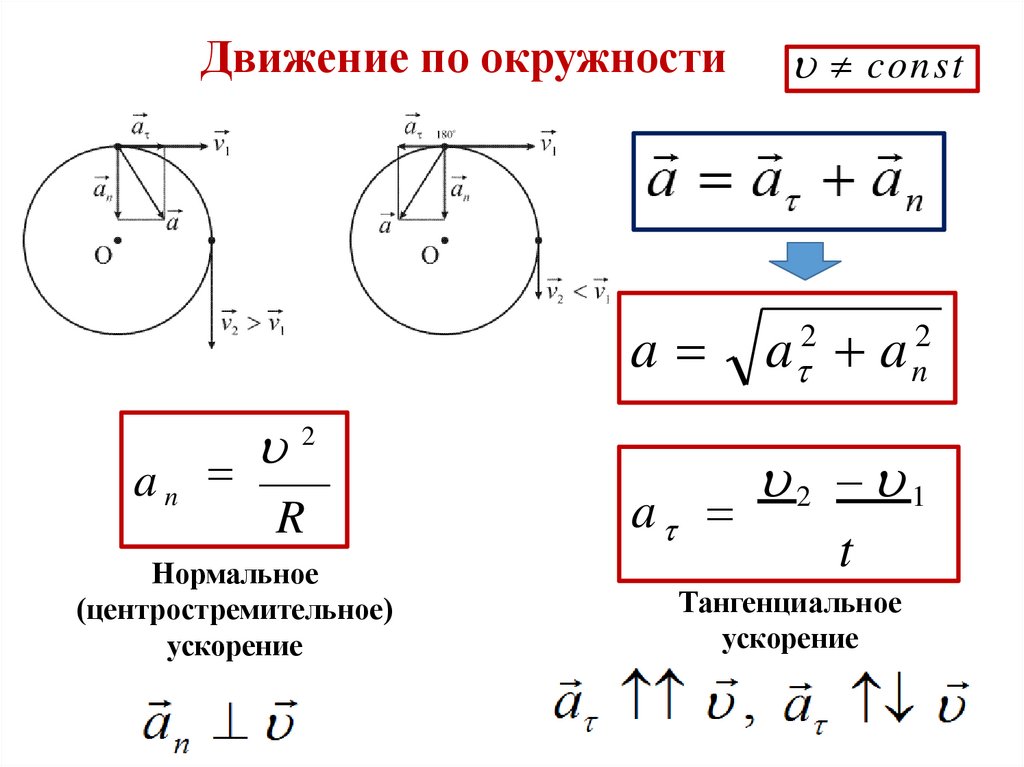
Движение по окружностиa
an
2
R
Нормальное
(центростремительное)
ускорение
a
const
a 2 a n2
2 1
t
Тангенциальное
ускорение
20.
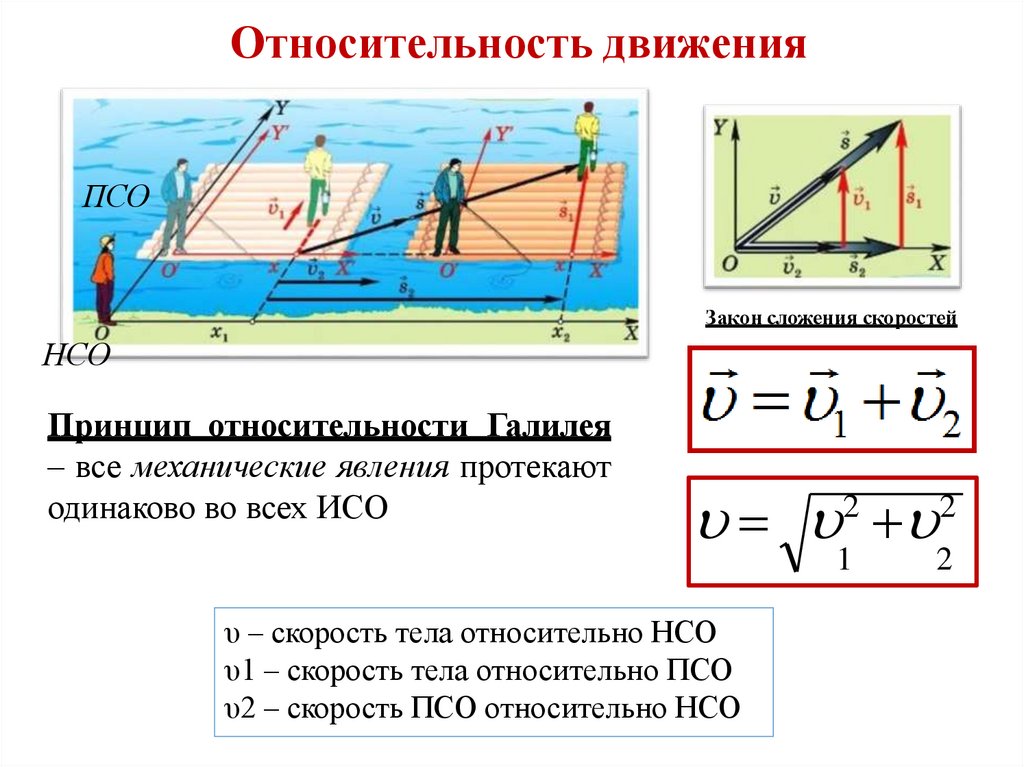
Относительность движенияПСО
Закон сложения скоростей
НСО
Принцип относительности Галилея
– все механические явления протекают
одинаково во всех ИСО
υ – скорость тела относительно НСО
υ1 – скорость тела относительно ПСО
υ2 – скорость ПСО относительно НСО
2
2
1
2
21.
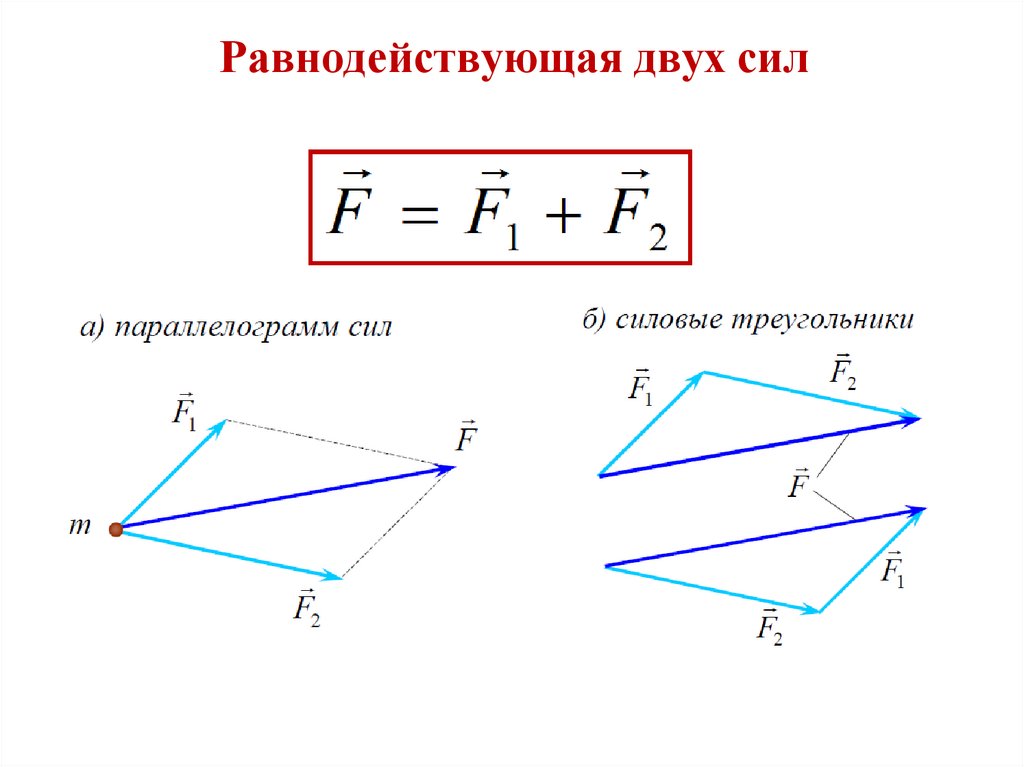
Основные понятия динамики22.
Равнодействующая двух сил23.
Первый закон Ньютона(закон инерции)
Существуют такие системы отсчета, относительно
которых поступательно движущееся тело сохраняет
свою скорость постоянной, если на него не действуют
другие тела или действие других тел скомпенсировано
Значение закона:
1) делит все СО на инерциальные и неинерциальные
2) объясняет причину покоя тела или его равномерного и
прямолинейного движения
Инерциальная СО – это СО, которая покоится или
движется равномерно и прямолинейно (а = 0)
24.
Почему Землю можно считатьинерциальной системой отсчета?
an
2
r
2 r
T
R 6370км
T 24ч 86400с
r R cos 53 0
6,28 6370000м 0,6 278 м
86400с
(278м / с) 2
м
an
0,01 2 0
6370000м
с
с
25.
Второй закон НьютонаУскорение тела прямо пропорционально силе, действующей
на него и обратно пропорционально массе тела:
Значение закона:
движения тела
объясняет
причину
F 1кг м2 1Н
с
ускоренного
26.
Третий закон НьютонаТела действуют друг на друга с силами равными по
модулю и противоположными по направлению:
Особенности силF1, F 2
:
1) одной природы;
2) появляются и исчезают парой;
3) их нельзя складывать, так как приложены к разным
телам.
27.
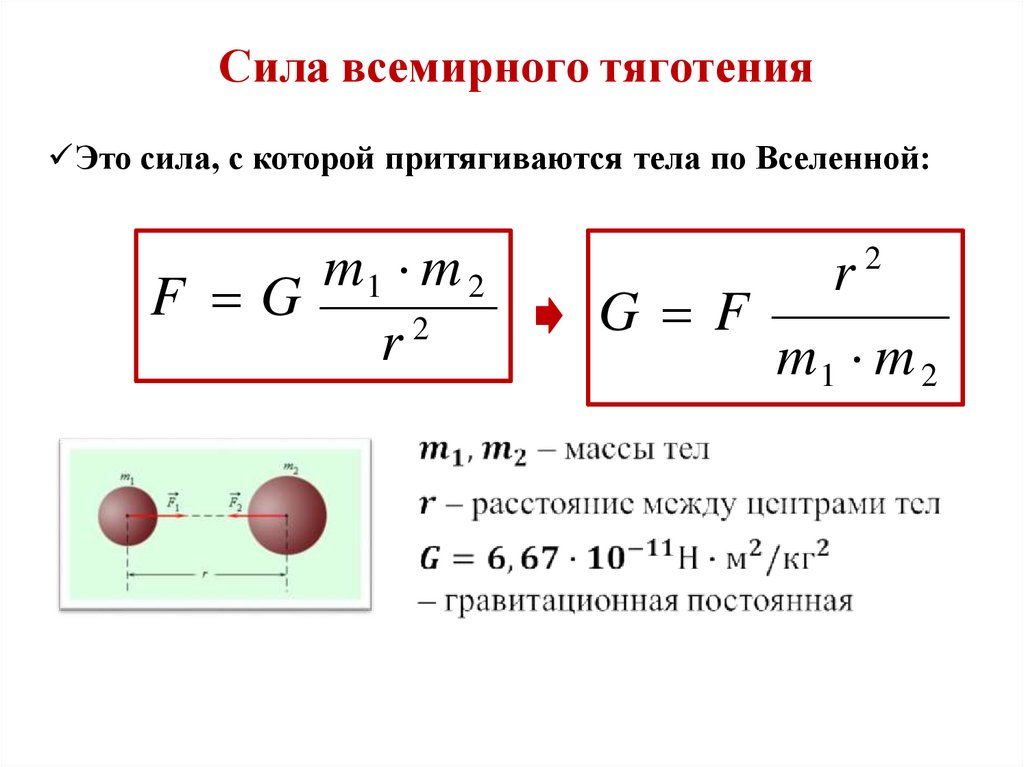
Силы в механике:Сила всемирного тяготения
Сила тяжести
Вес тела
Сила упругости
Сила реакции опоры
Сила натяжения
Сила трения (скольжения и
покоя)
Сила Архимеда
(выталкивающая сила)
28.
Сила всемирного тяготенияЭто сила, с которой притягиваются тела по Вселенной:
m1 m 2
F G
2
r
2
r
G F
m1 m 2
29.
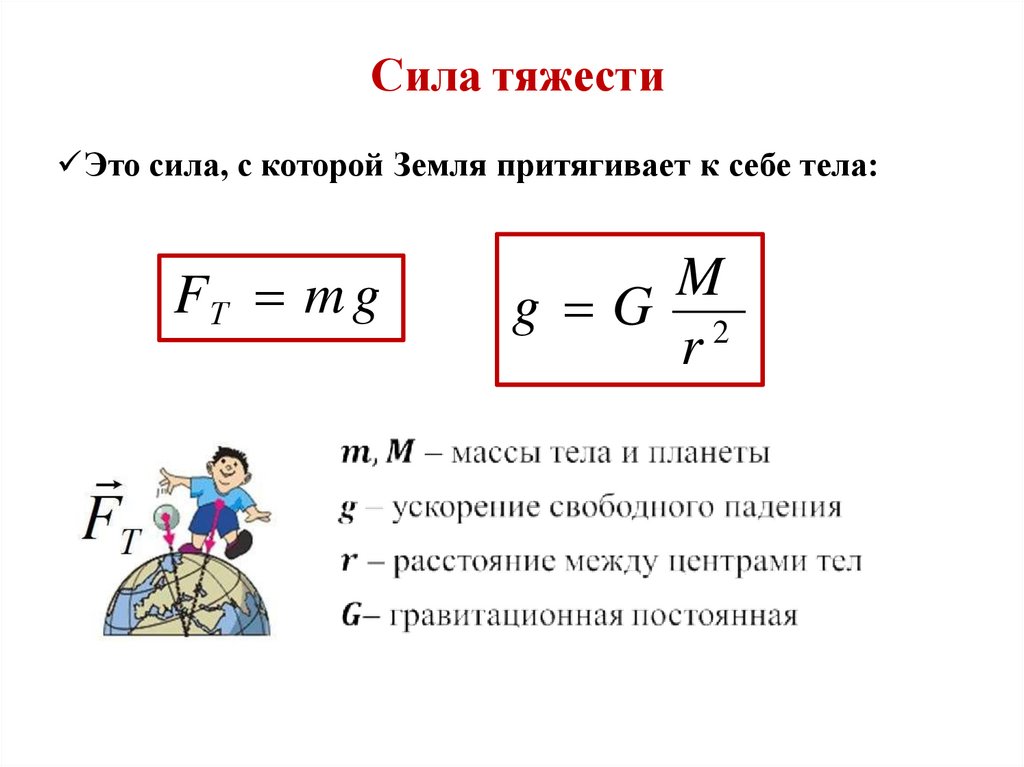
Сила тяжестиЭто сила, с которой Земля притягивает к себе тела:
FТ m g
M
g G 2
r
30.
Искусственные спутники Земли31.
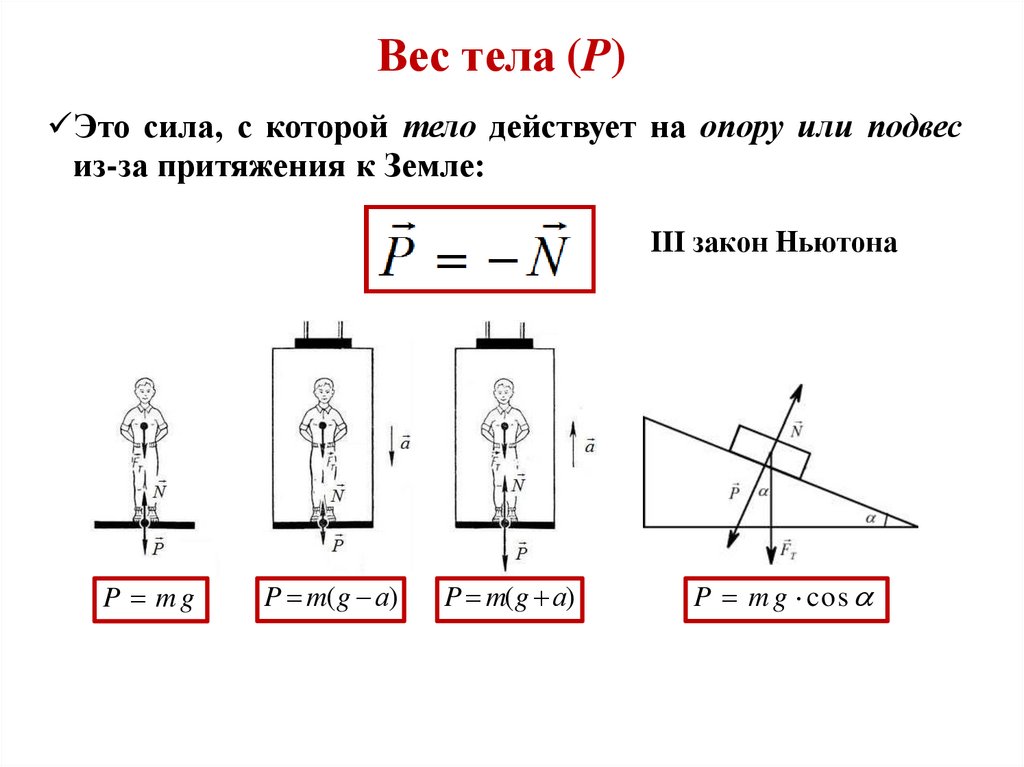
Вес тела (P)Это сила, с которой тело действует на опору или подвес
из-за притяжения к Земле:
III закон Ньютона
P mg
P m(g а)
P m(g а)
P m g cos
32.
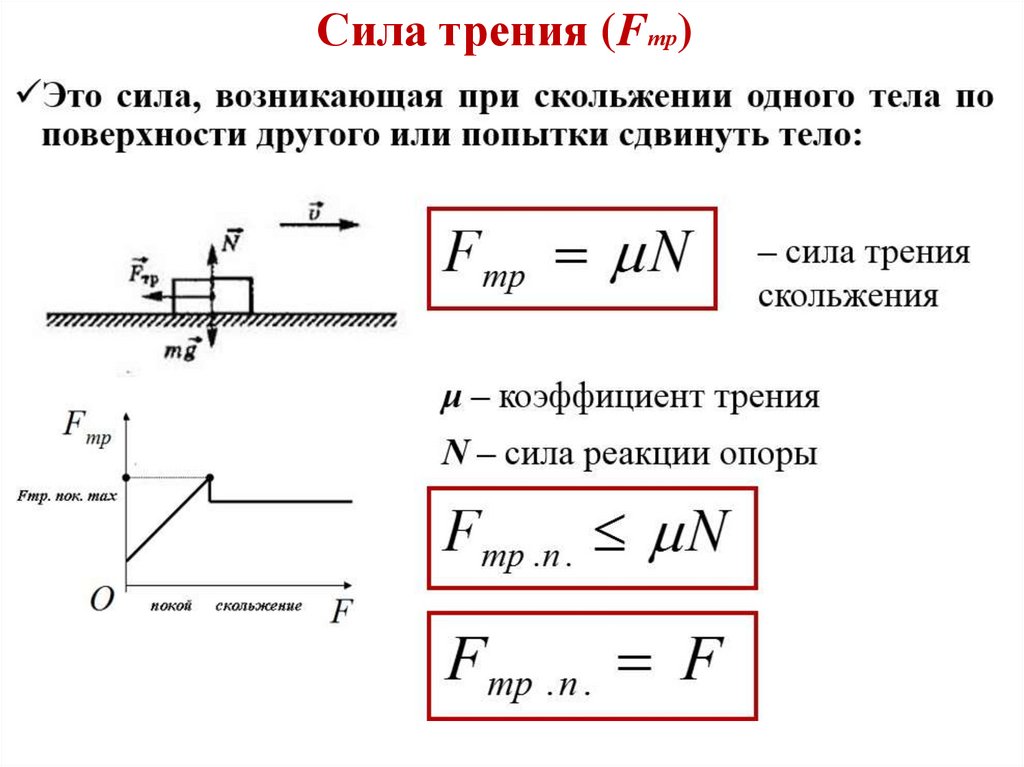
Сила упругостиЭто сила, возникающая при деформации и направленная
против нее:
(F У ) x k x
x – деформация
k – коэффициент
упругости (жесткость)
FУ k x
33.
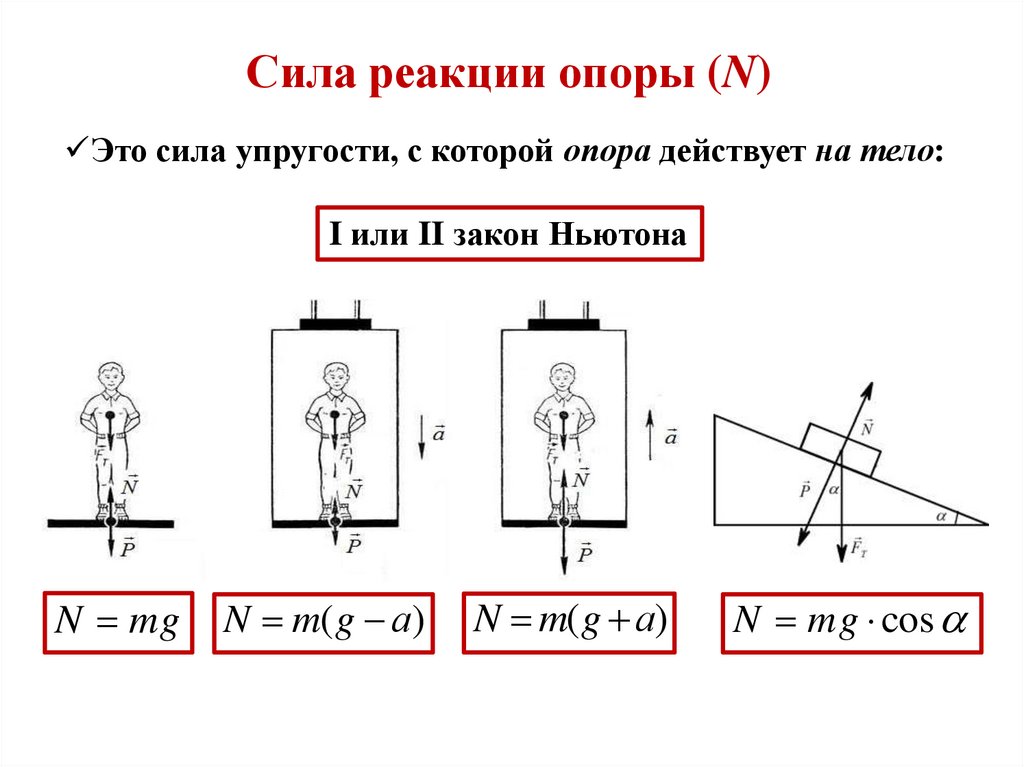
Сила реакции опоры (N)Это сила упругости, с которой опора действует на тело:
I или II закон Ньютона
N mg
N m(g а)
N m(g а)
N mg cos
34.
35.
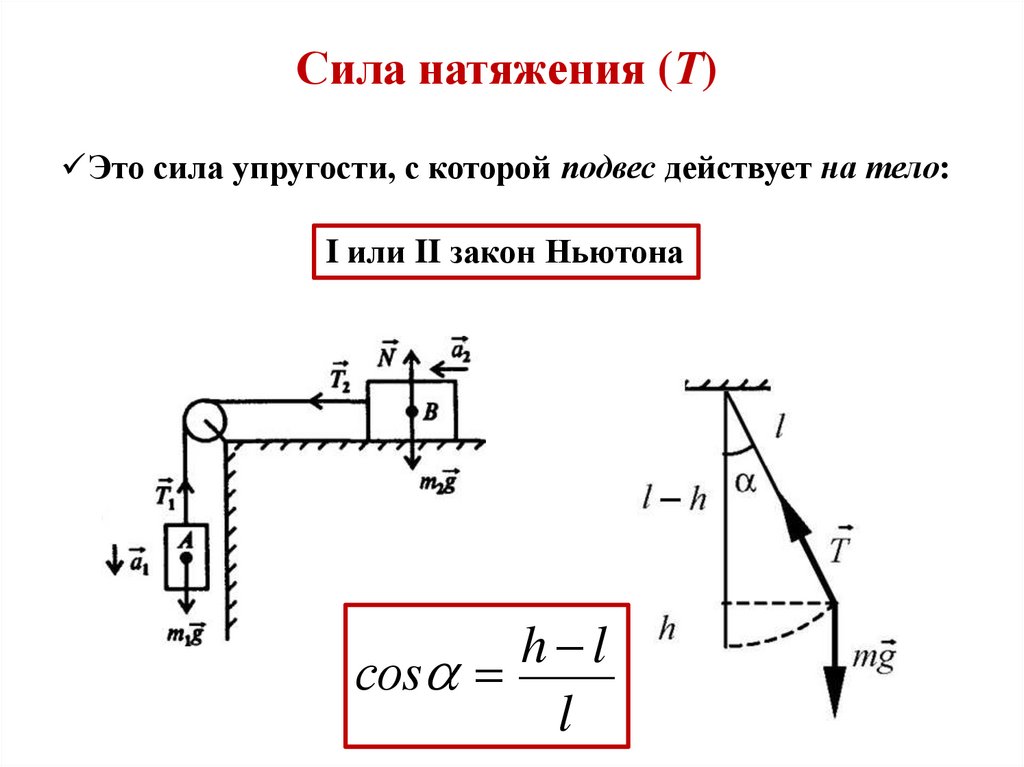
Сила натяжения (Т)Это сила упругости, с которой подвес действует на тело:
I или II закон Ньютона
h l
соs
l
36.
Сила трения (Fтр)37.
Сила Архимеда (выталкивающая сила)Это сила, с которой жидкость или газ выталкивает тело:
FА F2 F1
FА ж gV
F
р
gh
S
Н
р 1 м2 1Па
FА Рж
ρж – плотность жидкости
g – ускорение свободного падения
V – объем тела, погруженного в жидкость
h – высота столба жидкости
р – давление
38.
Физико-технический факультетТеория: законы сохранения, статика
39.
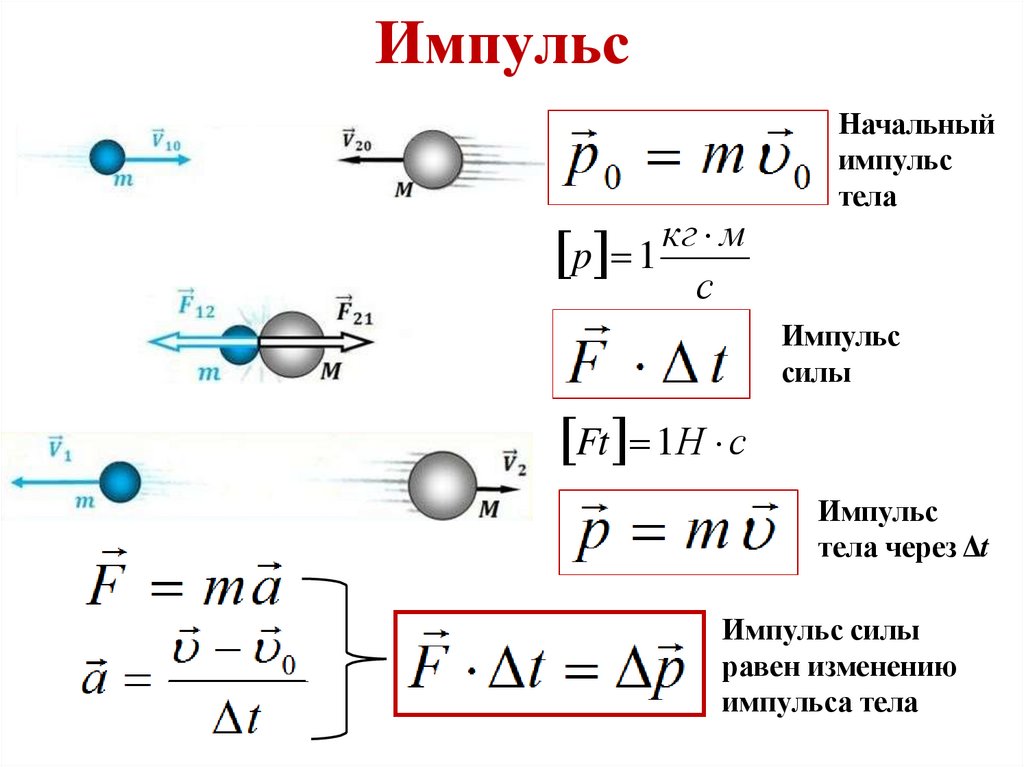
Импульскг м
p 1
с
Начальный
импульс
тела
Импульс
силы
Ft 1Н с
Импульс
тела через Δt
Импульс силы
равен изменению
импульса тела
40.
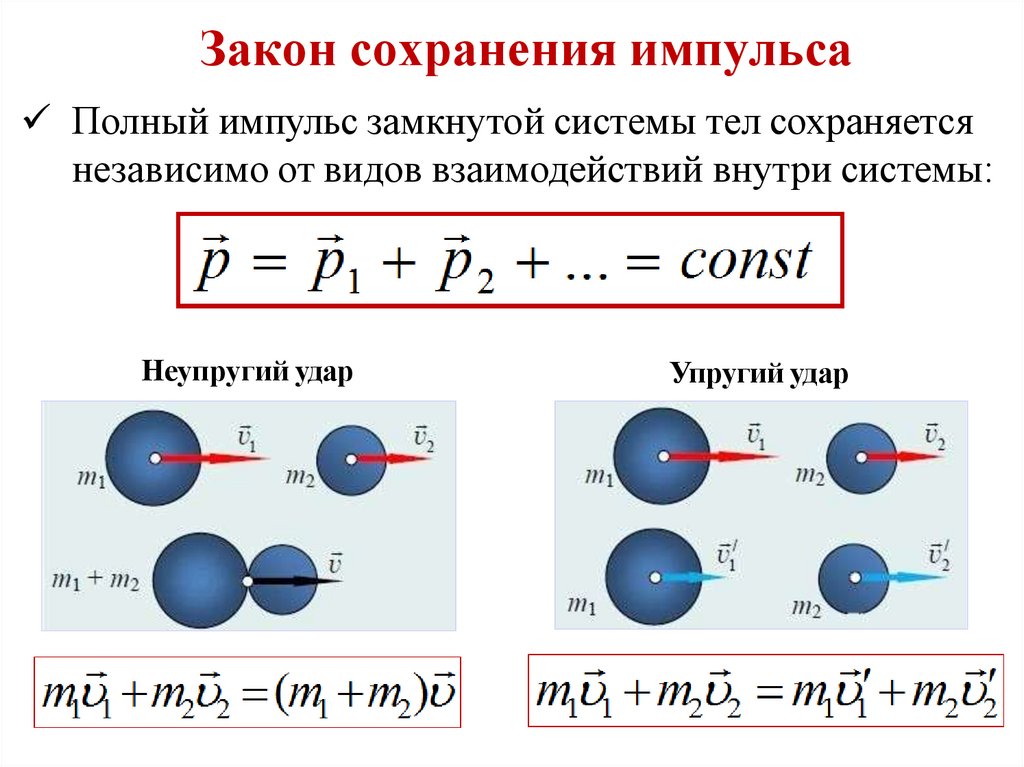
Закон сохранения импульсаПолный импульс замкнутой системы тел сохраняется
независимо от видов взаимодействий внутри системы:
Неупругий удар
Упругий удар
41.
Работа силы (А) и мощность (N)F const
A Fs cos
A Fs s
А 1Н м 1Дж
A
N F
t
N 1 Дж 1Вт
с
42.
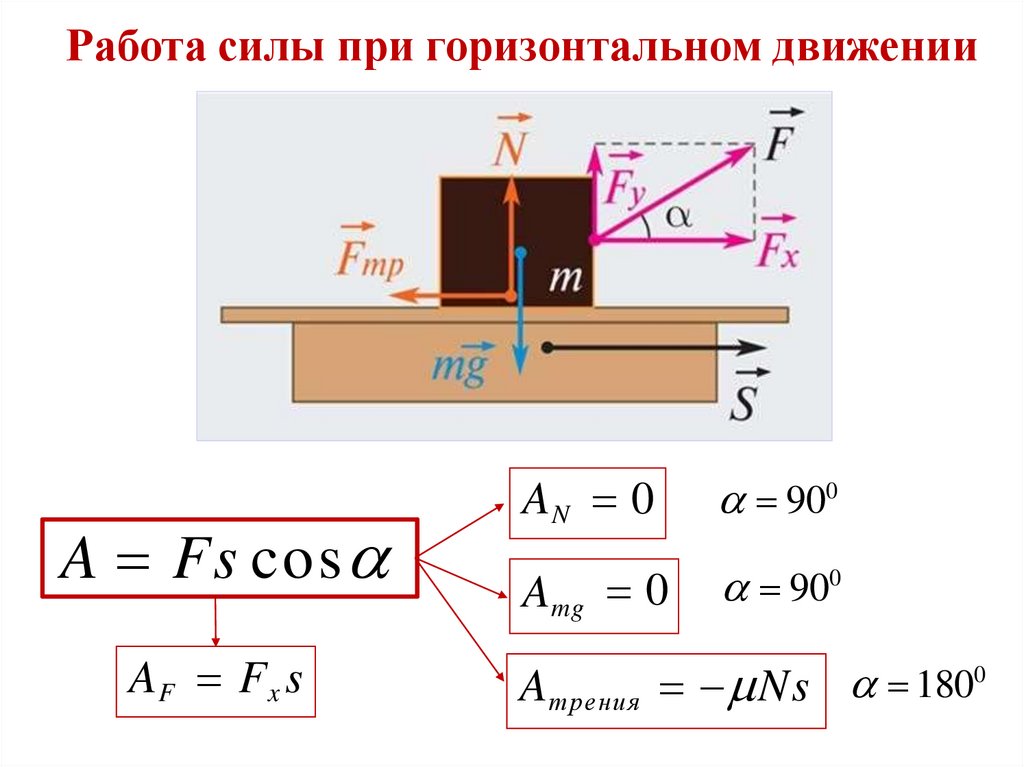
Работа силы при горизонтальном движенииA Fs cos
AF Fx s
AN 0
900
Amg 0
900
0
180
A трения Ns
43.
Потенциальная энергия (Ер)A Fs cos
F mg, s h h , cos 00 1
1
2
A mg(h1 h2 ) mgh1 mgh2
E p mgh
Потенциальная энергия
гравитационного
взаимодействия тела и Земли
A E p 1 E p 2 E p
Работа силы тяжести равна изменению
потенциальной энергии тела, взятому со знаком «–»
44.
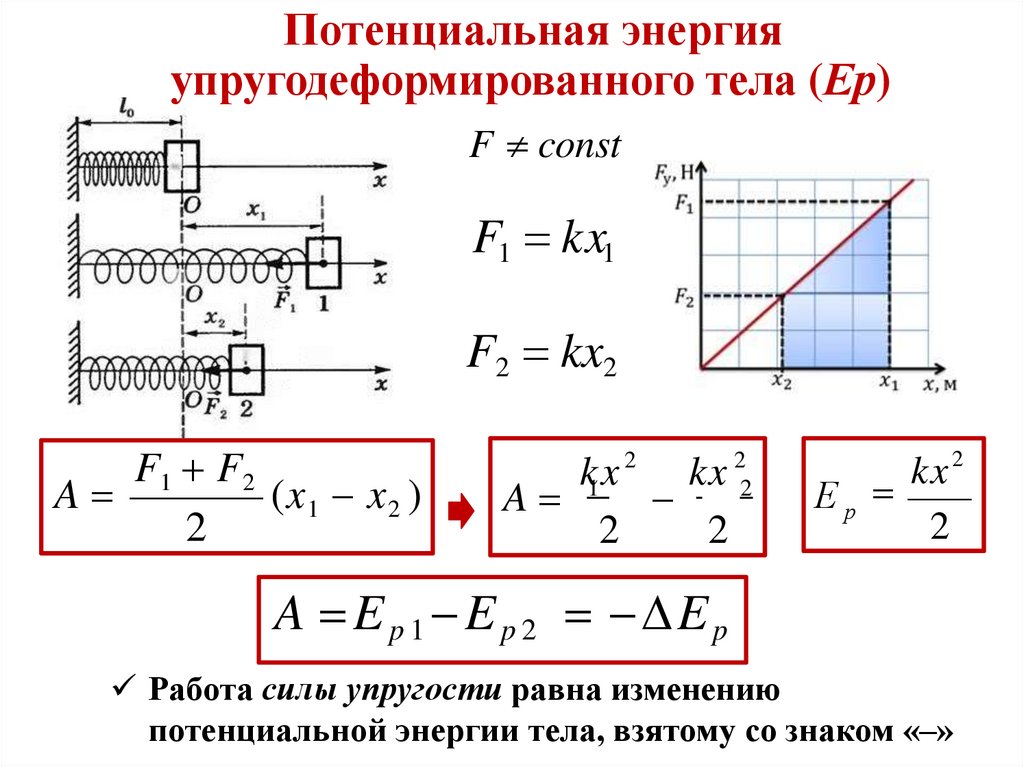
Потенциальная энергияупругодеформированного тела (Ер)
F const
F1 kx1
F2 kx2
F1 F2
A
(x 1 x 2 )
2
2
kx
kx
1
A
2
2
2
2
kx 2
Ер
2
A E p 1 E p 2 E p
Работа силы упругости равна изменению
потенциальной энергии тела, взятому со знаком «–»
45.
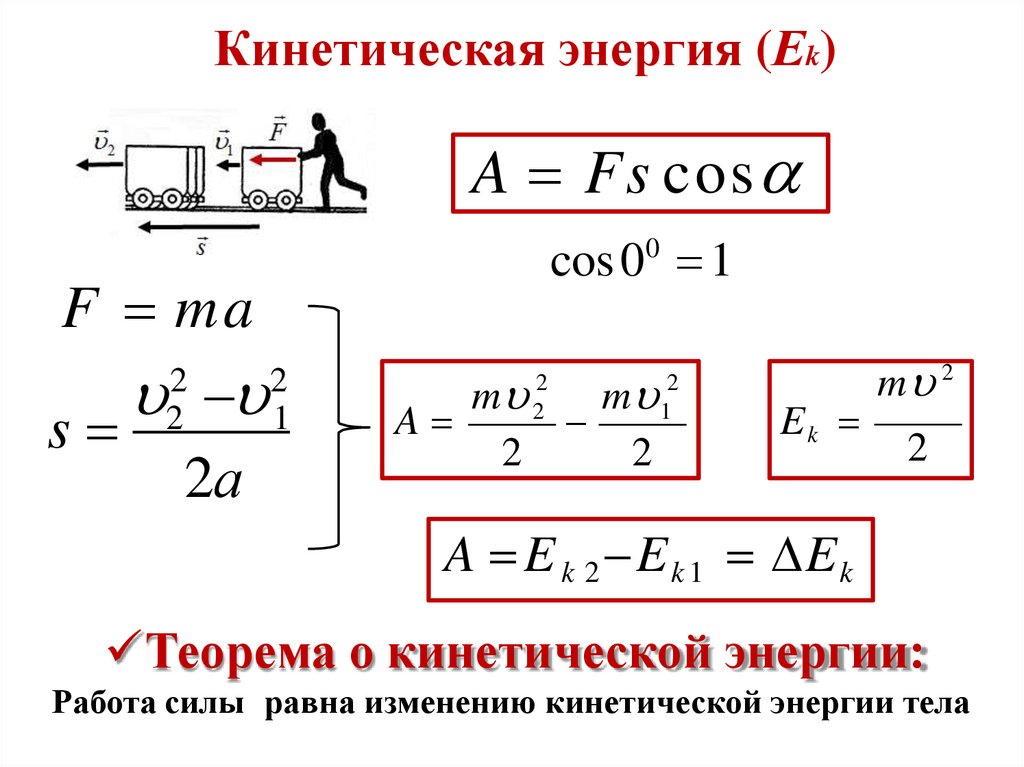
Кинетическая энергия (Еk)A Fs cos
F ma
2
2
2 1
s
2а
cos 00 1
m
m
A
2
2
2
2
2
1
Ek
m 2
2
A E k 2 E k 1 E k
Теорема о кинетической энергии:
Работа силы равна изменению кинетической энергии тела
46.
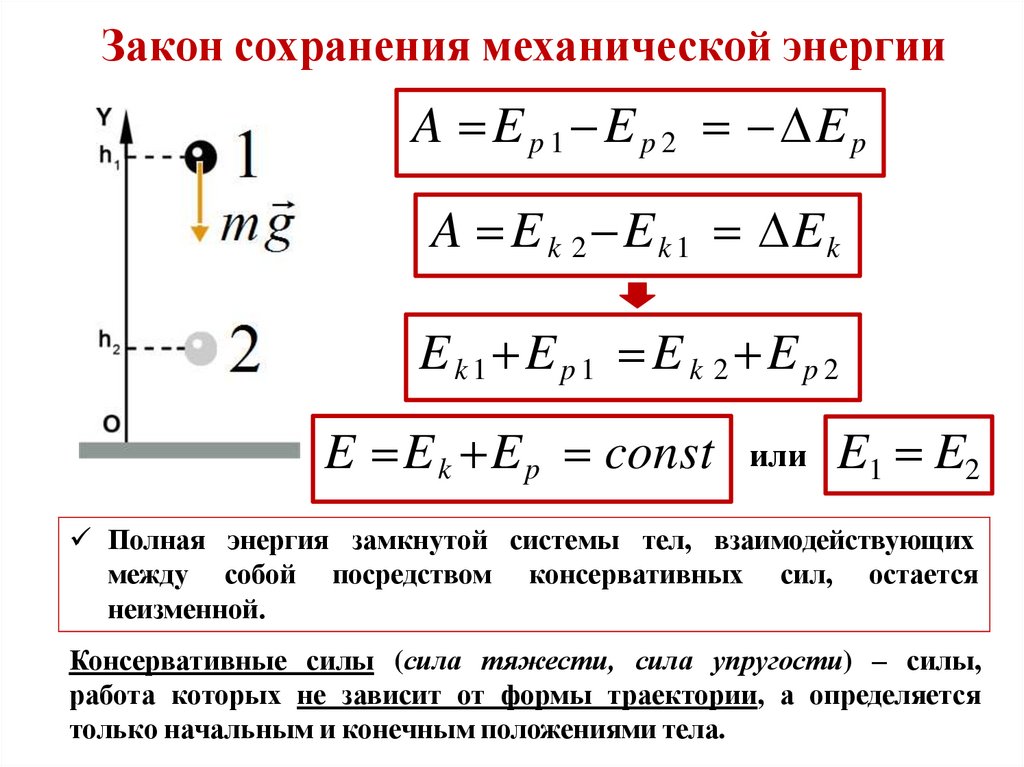
Закон сохранения механической энергииA E p 1 E p 2 E p
A E k 2 E k 1 E k
E k 1 E p 1 E k 2 E p 2
E E k E p const или E1 E2
Полная энергия замкнутой системы тел, взаимодействующих
между собой посредством консервативных сил, остается
неизменной.
Консервативные силы (сила тяжести, сила упругости) – силы,
работа которых не зависит от формы траектории, а определяется
только начальным и конечным положениями тела.
47.
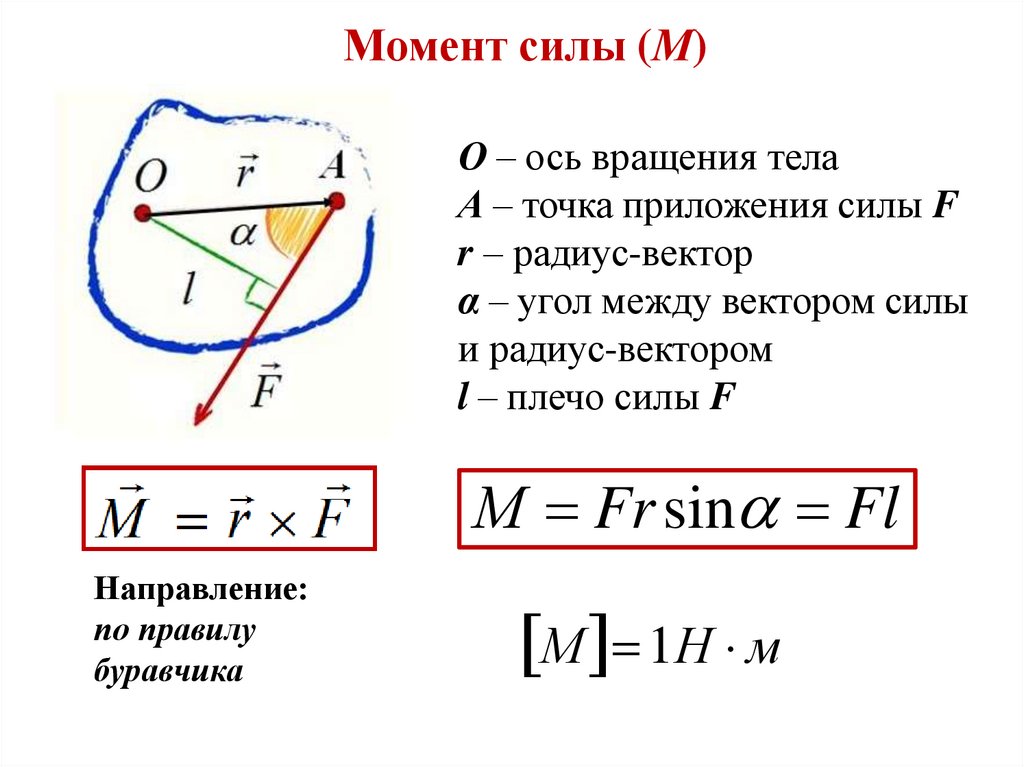
Момент силы (М)О – ось вращения тела
А – точка приложения силы F
r – радиус-вектор
α – угол между вектором силы
и радиус-вектором
l – плечо силы F
М Fr sin Fl
Направление:
по правилу
буравчика
М 1Н м
48.
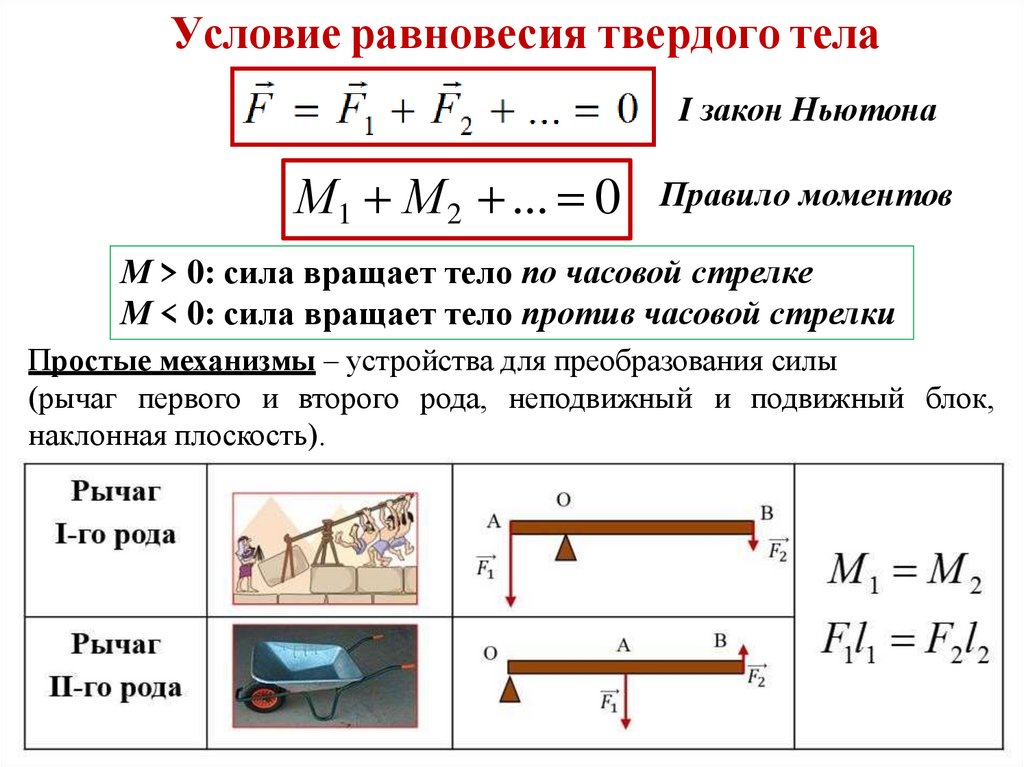
Условие равновесия твердого телаI закон Ньютона
М1 М 2 ... 0
Правило моментов
М > 0: сила вращает тело по часовой стрелке
М < 0: сила вращает тело против часовой стрелки
Простые механизмы – устройства для преобразования силы
(рычаг первого и второго рода, неподвижный и подвижный блок,
наклонная плоскость).
49.
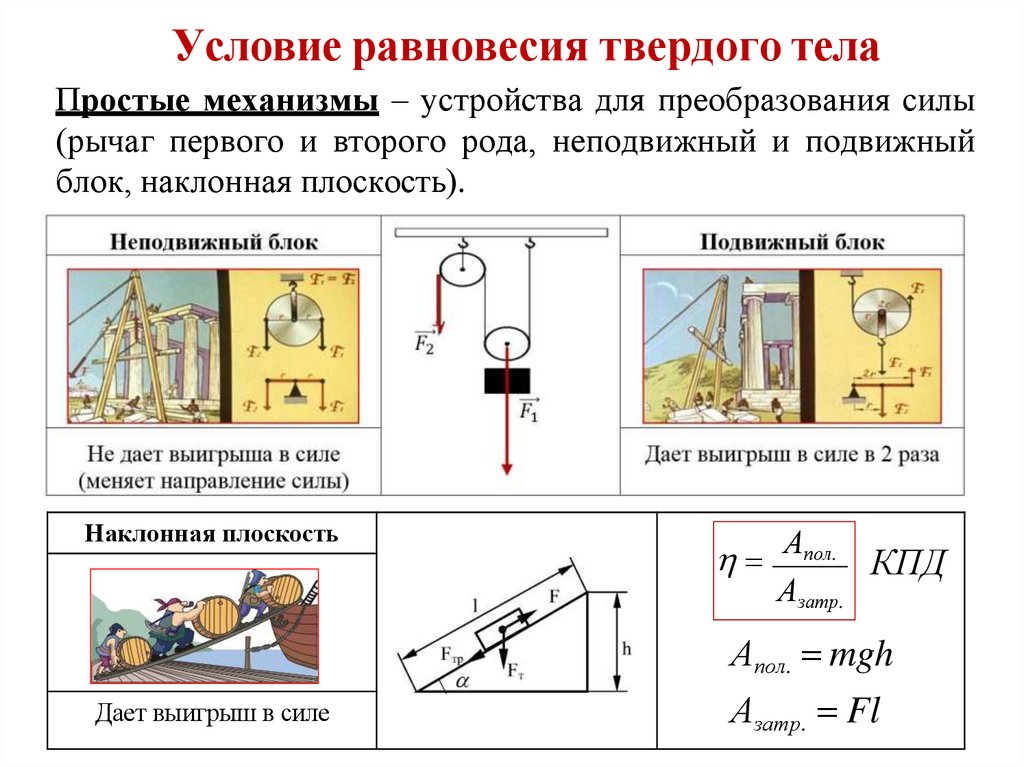
Условие равновесия твердого телаПростые механизмы – устройства для преобразования силы
(рычаг первого и второго рода, неподвижный и подвижный
блок, наклонная плоскость).
Наклонная плоскость
Апол. КПД
Азатр.
Апол. mgh
Дает выигрыш в силе
Азатр. Fl
50.
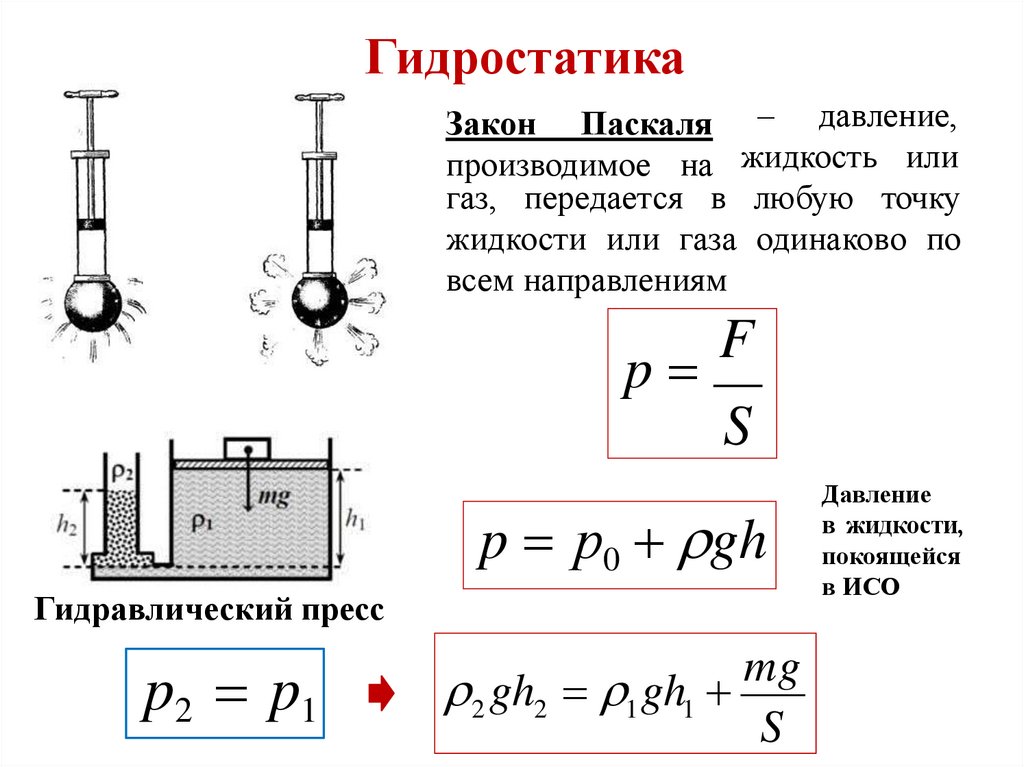
ГидростатикаЗакон Паскаля – давление,
производимое на жидкость или
газ, передается в любую точку
жидкости или газа одинаково по
всем направлениям
p
F
S
p р0 gh
Гидравлический пресс
p2 p1
mg
2 gh2 1 gh1
S
Давление
в жидкости,
покоящейся
в ИСО
51.
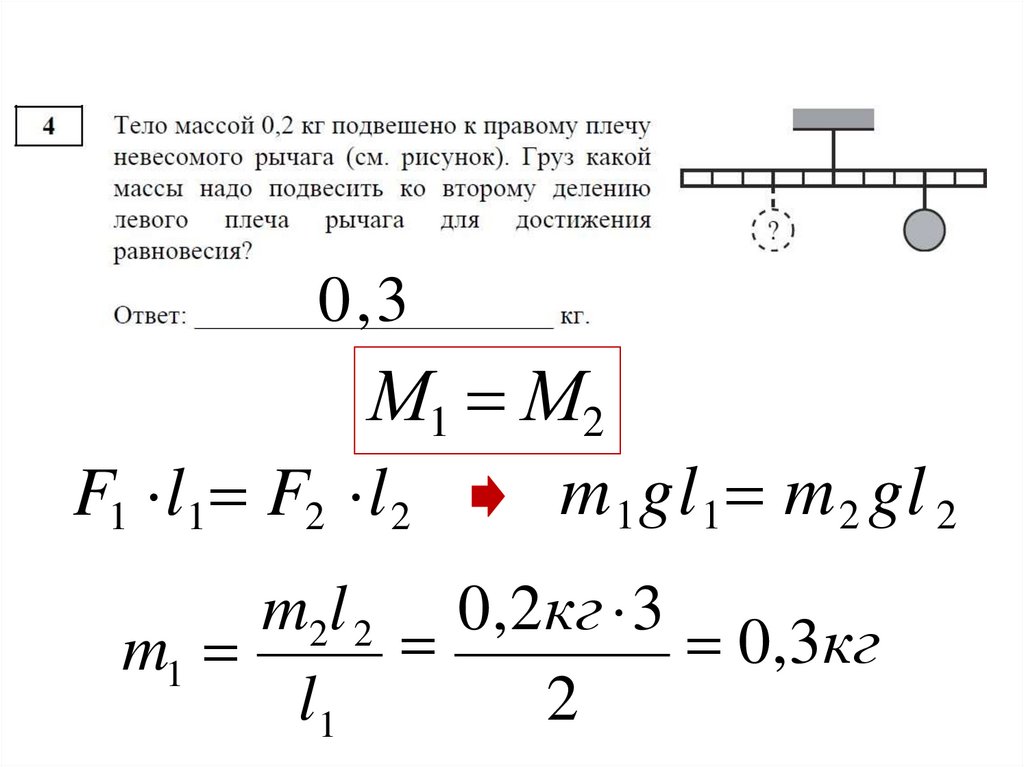
0,3М1 М2
m 1 gl 1 m 2 gl 2
F1 l 1 F2 l 2
m2l 2 0,2кг 3
0,3кг
m1
l1
2
52.
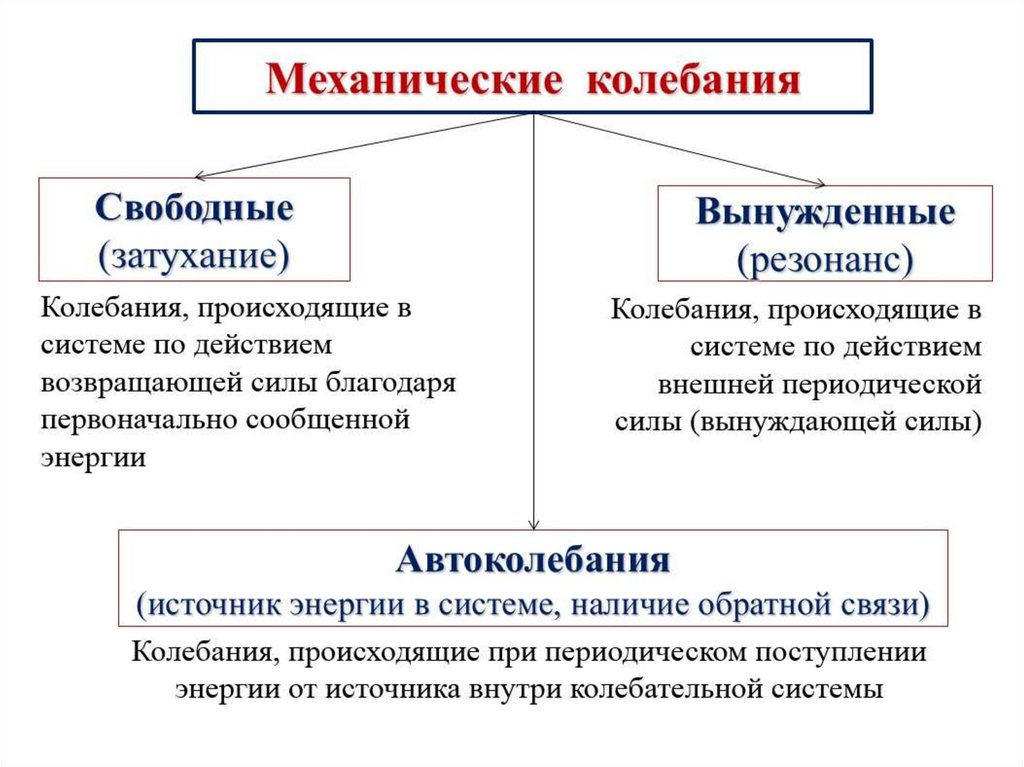
Механическиеколебания и волны
53.
54.
Характеристики колебательного процесса55.
Характеристики колебательного процессаАмплитуда (А, xm) – максимальное смещение тела от
положения равновесия, м (метр)
Период (T) – промежуток времени, в течение которого
совершается одно полное колебание, с (секунда)
Частота (ν) – количество колебаний за 1 с, Гц (герц)
Циклическая частота (ω) – количество колебаний за
2π с, рад/с (радиан в секунду)
Фаза (φ) – угловая мера времени (аргумент sin или
cos), рад (радиан)
t N 1
T
t
T
N
2
2
2
t t
T
T
56.
Закон сохранения энергииFc 0
A const
E Ek E p const
E
kx2
2
m 2
2
m 2
kA2
2
2
m
Полная
механическая
энергия
2
x(t) Acos 0t
kx
2
Ecos 0t
Ep (t)
2
x (t) m sin 0t
m 2
2
Esin 0t
Ek (t)
2
57.
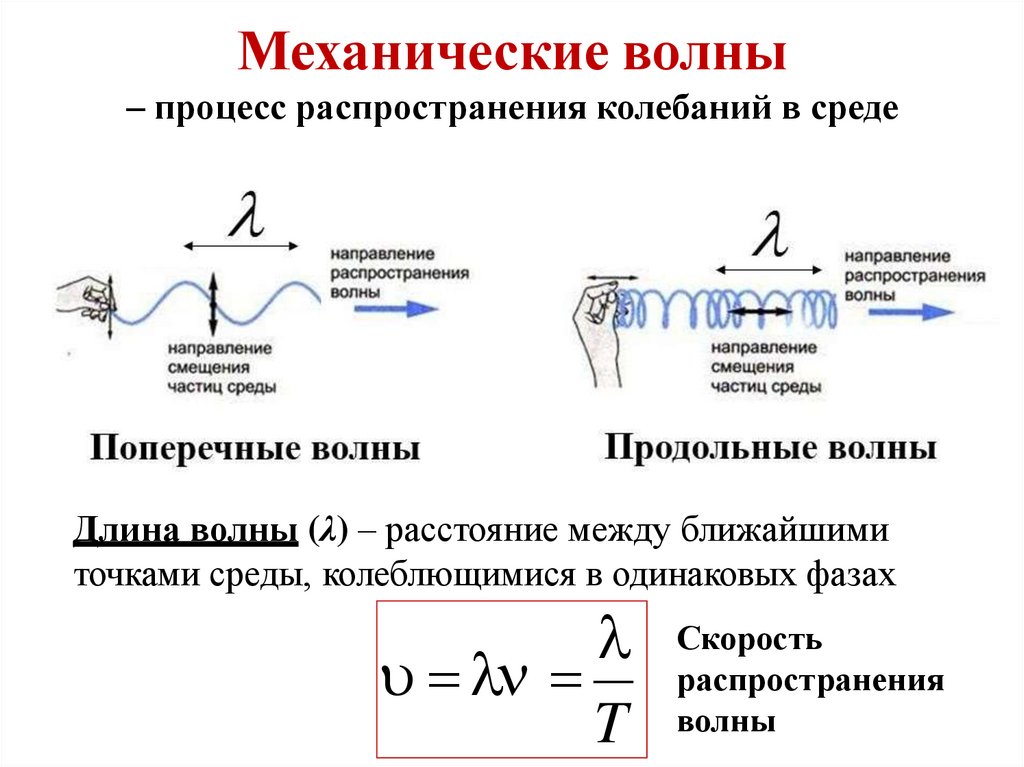
Механические волны– процесс распространения колебаний в среде
Длина волны (λ) – расстояние между ближайшими
точками среды, колеблющимися в одинаковых фазах
T
Скорость
распространения
волны
58.
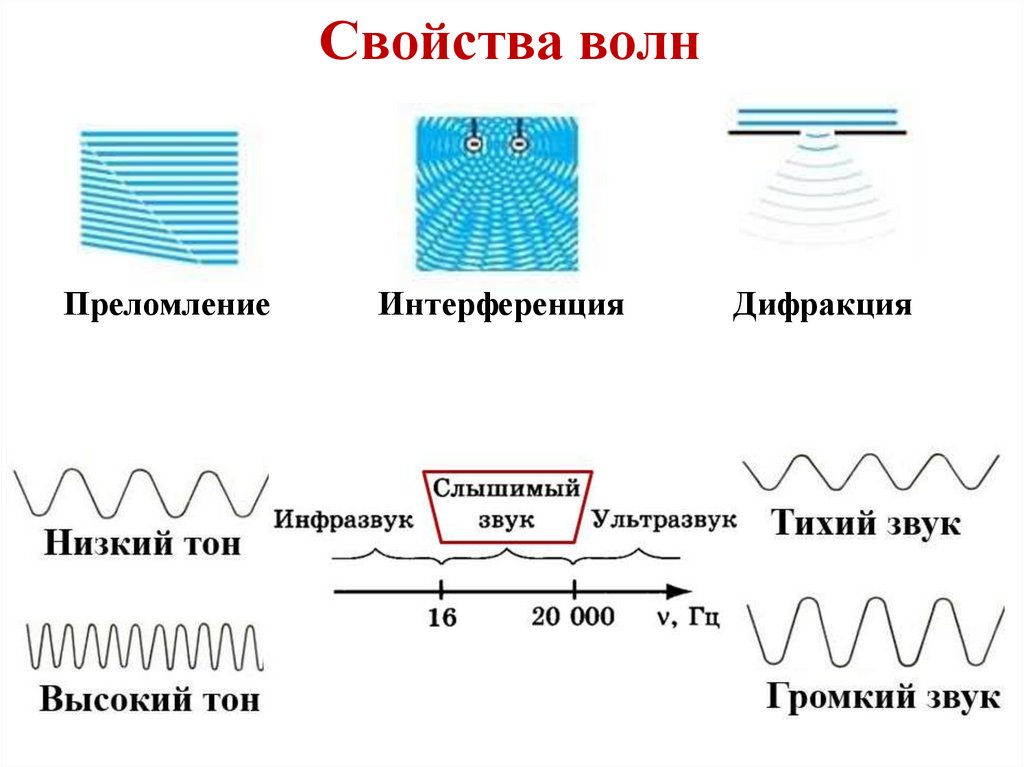
Свойства волнПреломление
Интерференция
Дифракция



























 physics
physics








