Логарифмическая функция

1.

Логарифмическая функция»
.
Подготовила:
Учитель математики
ГБОУ СОШ №81 Калининского района
г.Санкт-Петербург
Круглова М.В.

2.

Тема урока:
Логарифмическая функция
• “Истинное знание состоит не
в знакомстве с фактами,
которое делает человека
лишь педантом, а в
использовании фактов,
которое делает его
философом”.
Г. Бокль

3.

Цели урока:
1)Обобщение и систематизация
теоретического материала по данной теме.
2) Отработка умений и навыков применения формул
. для преобразования логарифмических выражений
и решения уравнений в контексте с требованиями ЕГЭ.
3) Развитие навыков работы с дополнительной литературой,
с историческим материалом.

4.

Потому-то, словно пена,
Опадают наши рифмы.
И величие степенно ,
отступает в логарифмы
Б.Слуцкий.
теория
практика

5.

Этапы урока
1.Устная работа.
2.Логарифмическая функция и ее
график.
3.Методы решения логарифмических
уравнений.
4.Самостоятельная работа (задание на
доске)
5. “Логарифмы в жизни и в природе”

6.

Работа устно:
№
a
b
c
d
1
2
3
4
Е
Н
Е
Р
П
6

7.

Джон Непер
John Napier
Дата рождения:
1550 год
Место рождения:
предместье Эдинбурга
Дата смерти:
4 апреля 1617
Место смерти:
Эдинбург
Научная сфера:
математика
Альма-матер:
Сент-Эндрюсский университет
Известен как:
изобретатель логарифмов

8.

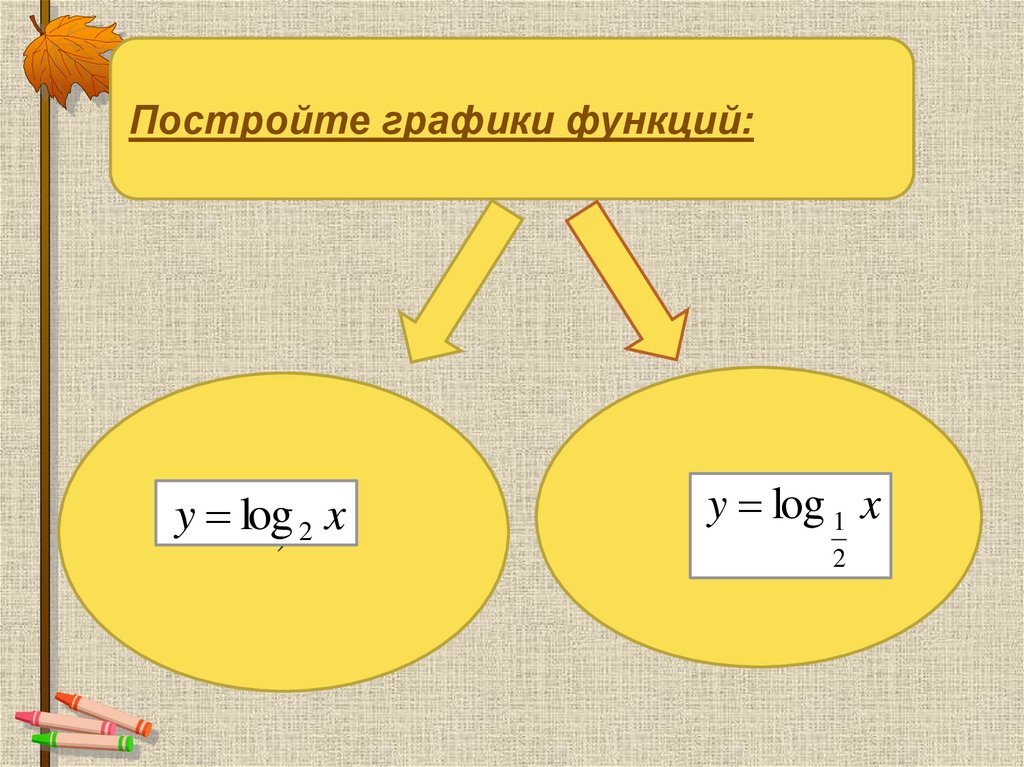
Постройте графики функций:
y log) 2 x
y log 1 x
2

9.

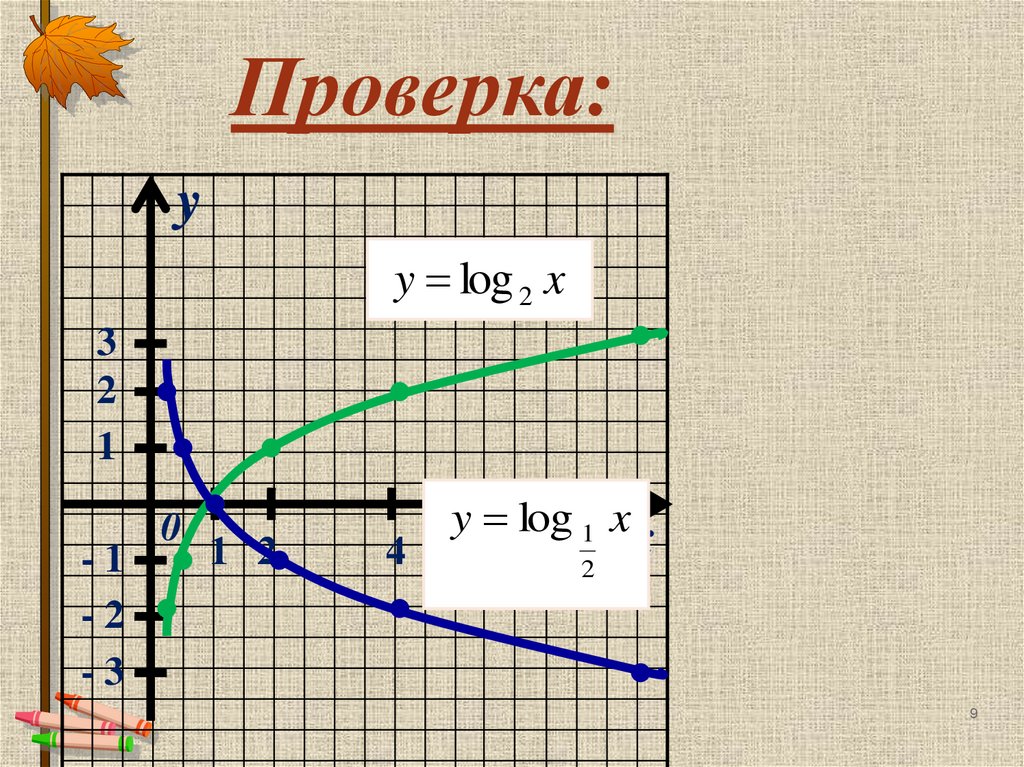
Проверка:
y
y log 2 x
3
2
1
-1
-2
-3
0
1 2
4
y log 1 x
28
x
9

10.

свойства
логарифмической
функции.
y log a x, a 1
Логарифмическая
функция
y log a x,
0 a 1

11.

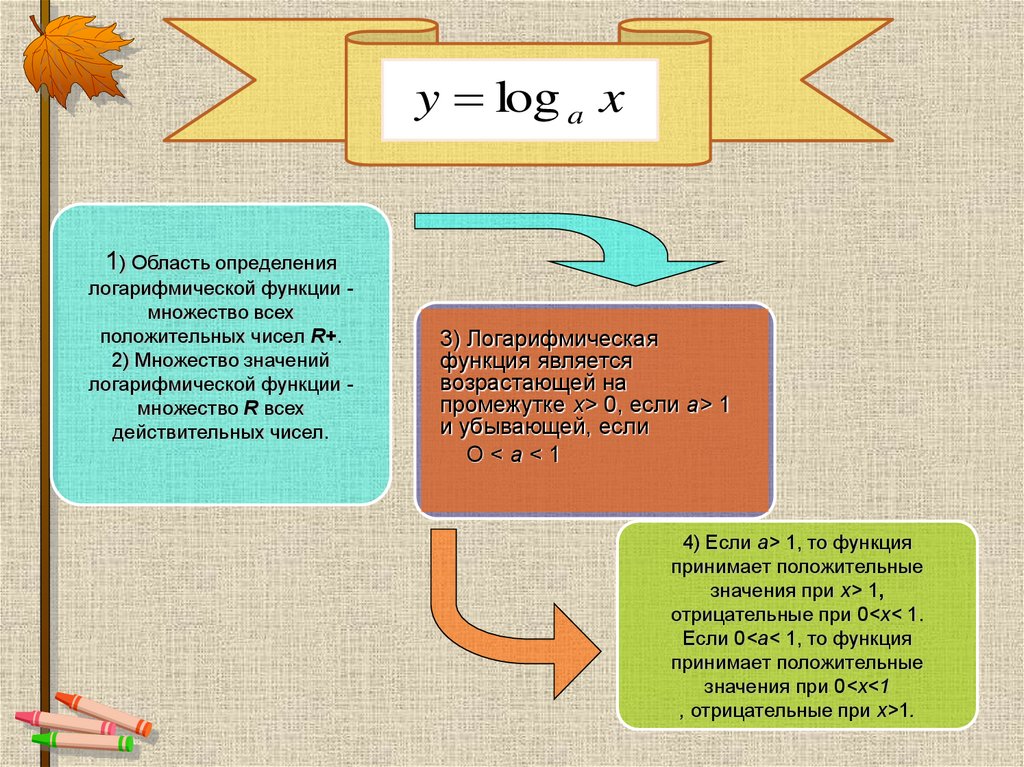
y log a x
1) Область определения
логарифмической функции множество всех
положительных чисел R+.
2) Множество значений
логарифмической функции множество R всех
действительных чисел.
3) Логарифмическая
функция является
возрастающей на
промежутке х> 0, если а> 1
и убывающей, если
О<а<1
4) Если а> 1, то функция
принимает положительные
значения при х> 1,
отрицательные при 0<х< 1.
Если 0<а< 1, то функция
принимает положительные
значения при 0<х<1
, отрицательные при х>1.

12.

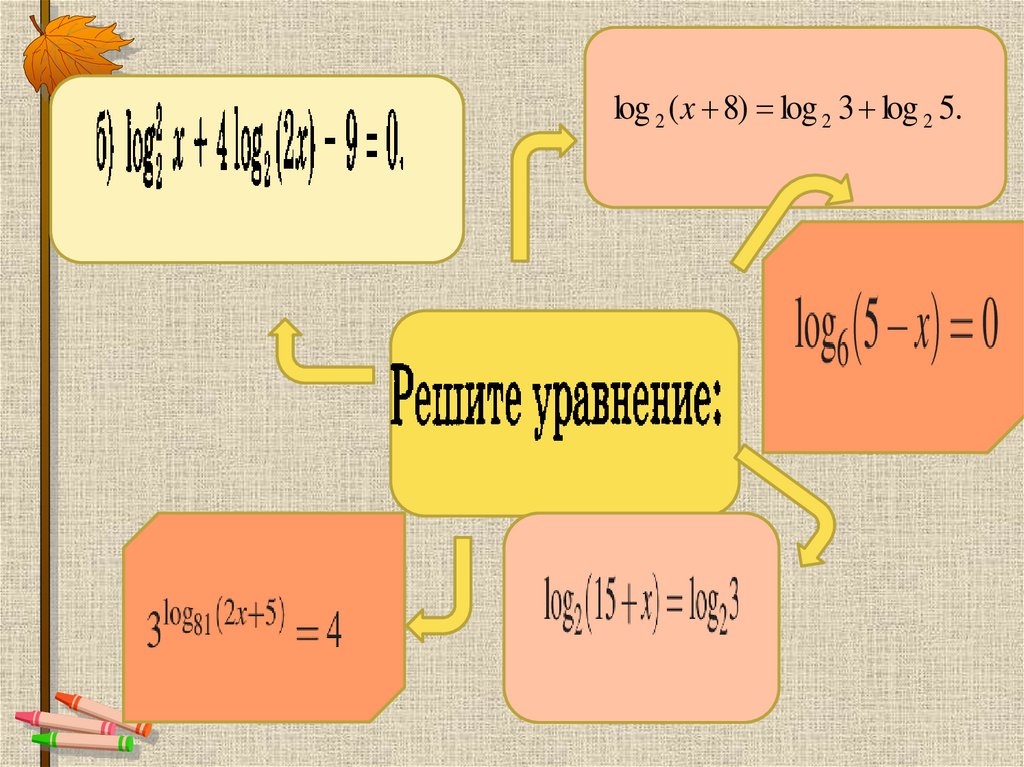
Методы решения логарифмических
уравнений.

13.

log 2 ( x 8) log 2 3 log 2 5.

14.

. Динамическая пауза или разрядка для глаз
• (исходное положение - сидя, каждое упражнение
повторяется 3-4 раза):
• 1. Откинувшись назад, сделать глубокий
вдох, затем, наклонившись вперед, выдох.
• 2. Откинувшись на спинку стула, прикрыть
веки, крепко зажмурить глаза, не открывая
век.
• 3. Руки вдоль туловища, круговые
движения плечами назад и вперёд.

15.

Вашему вниманию представлены задания взятые
из КИМов
log 2 0,04 2 log 2 5
.1 Вычислите:
2 Какому промежутку принадлежит
корень уравнения
log 2 ( x 8) log 2 3 log 2 5.
1) (-∞;-5] ; 2) (-1;3) ; 3) (3;5) ; 4) [5;8] .
3 Найдите значение выражения
log
20
5 log
20
4 2
5. Найдите сумму всех целых чисел, входящих в область
определения
6 Найти корни уравнения
у = lg ( х - 2| х - 3 | ) .
6
3
2
2 log 12 ( x
) log 12 (
) 3.
x 5
x 2 x 3

16.

Путешествие на северо-восток
Вопрос: Если идти все время
на северо-восток, то куда
придешь?
• Ответ: Рано или поздно мы
попадем на северный полюс.
• При этом путь, который мы
пройдем, будет иметь вид
логарифмической спирали.

17.

Логарифмическая спираль в природе
Хищные птицы кружат над добычей по логарифмической спирали.
Дело в том, что они лучше видят, если смотрят не прямо на добычу,
а чуть в сторону.
Раковины многих моллюсков, улиток,
а также рога горных козлов закручены по
логарифмической спирали

18.

ЗВЕЗДЫ И ЛОГАРИФМЫ
Астрономы делят звезды по степени яркости на
видимые и абсолютные звездные величины звезды первой величины, второй, третьей и т. д.
физическая их яркость изменяется по иному
закону: яркости звезд составляют геометрическую
прогрессию со знаменателем 2,5.
Легко понять, что «величина» звезды
представляет собой логарифм ее
физической яркости.
Астроном, оценивая яркость звезд, оперирует
таблицей логарифмов, составленной при
основании 2,5.

19.

ЛОГАРИФМЫ И ОЩУЩЕНИЯ
Ощущения, воспринимаемые органами чувств
человека,
могут вызываться раздражениями, отличающимися
друг от друга во много миллионов и даже миллиардов
раз.
Удары молота о скользкую плиту в сто раз громче, чем
тихий шелест листьев, а яркость вольтовой дуги в
триллионы раз превосходит яркость какой-нибудь
слабой звезды, едва видимой на ночном небе. Но
никакие физиологические процессы не позволяют дать
такого диапазона ощущений.
Опыты показали, что организм как бы логарифмирует»
полученные им раздражения, т.е. величина ощущения
приблизительно пропорциональна десятичному
логарифму величины раздражения. Как видим,
логарифмы вторгаются и в область психологии.

20.

Рефлексия (итог урока)
- Что нового узнали на уроке?
- Что повторили?
- Чью работу вы можете
отметить?
- Как оцениваете свою работу?

21.

22.

Источники информации
• Энциклопедия для детей. Т.11. Математика/Глав.
ред.М.Д. Аксёнова. – М.: Авантаж, 1998.-688 с.
• Что такое математика? /В.И.Арнольд. — М.: МЦНМО,
2008.–– 104 с.
• http://www.allmath.ru/bestbooks.htm
• http://www.exponenta.ru - Exponenta образовательный математический сайт
• http://www.gordia.ru/gm.php - математика жизни.

23.

Источники информации
• Алимов Ш.А. «Алгебра и начала анализа». Москва.
Просвещение. 2018 г.
• Шарыгин И.Ф. «Факультативный курс по математике. Решение
задач. 11 кл» Москва. «Просвещение». 1991 год.
• «Математика. Подготовка к ЕГЭ – 2017 Тематические
тесты»/Под редакцией Лысенко Ф.Ф. – Ростов н/Д: Легион – М,
2017
• Программы для общеобразовательных учреждений (школ,
гимназий, лицеев): Математика, 5-11 кл./ СоставителиГ.М.
Кузнецова, Н.Г. Миндюк. – М.: Дрофа, 2013
• Электронные ресурсы: www.fipi.ru, свободный доступ
• Электронные ресурсы: www.ege.edu.ru, свободный доступ