«С точки зрения вычислительной практики, изобретение логарифмов по важности можно смело поставить рядом с другим, более древним

Русский математик Аничков Д. С. о логарифмах

Друзья, поверьте: Самая интересная, полезная и лирическая Это – функция логарифмическая.

И уравнения решая Должны мы все не забывать, Что ОДЗ и логарифмы Вместе нужно записать!

Закручены по ней рога козлов И не найдете вы на них узлов.

Наверняка, и о том вы не знали, Галактики тоже кружат по спирали!

2.27M

Category: $mathematics$ mathematics

Бенефис логарифмической функции

1. Бенефис логифмической функции

2. «С точки зрения вычислительной практики, изобретение логарифмов по важности можно смело поставить рядом с другим, более древним

великим
изобретением индусов – нашей
десятичной системой
нумерации».
Я. В. Успенский

3.

Есть в математике тема одна,
Логарифмической функцией
называется она.
Логарифм появился, чтобы легче
считать,
Логарифм – п о к а з а т е л ь, это
надо знать!

4. Из истории логарифмов

Слово логарифм
происходит от греческого
λογοφ (число) и ρίνμοφ (отношение) и
переводится, следовательно, как отношение
чисел. Выбор изобретателем (1594 г.)
логарифмов Джоном Непером такого
названия объясняется тем, что логарифмы
возникли при сопоставлении двух чисел,
одно из которых является членом
арифметической прогрессии, а другое –
геометрической.

5. Русский математик Аничков Д. С. о логарифмах

«Ежели под геометрическою прогрессиею,
начинающеюся с единицы, подписана будет
арифметическая прогрессия, начинающаяся с нуля,
то числа, внизу подписанные, называются для
верхних – логарифмы.
Положим, что даны прогрессии:
геом.
1, 2, 4, 8, 16, 32, 64, 128, 256,
арифм.
0, 1, 2, 3, 4, 5, 6,
7,
Тогда логарифм 1 будет 0;
логарифм 4 будет 2;
а логарифм 32 будет 5 и проч.»
8.

6. Друзья, поверьте: Самая интересная, полезная и лирическая Это – функция логарифмическая.

Проходит график через точку (1;0)
И в том еще у графика есть соль,
Что в правой полуплоскости он «стелется»,
А в левую попасть и не надеется.
Сама же функция порою убывает,
А командиром служит ей значенье а
И подчиняется она ему всегда.

7. И уравнения решая Должны мы все не забывать, Что ОДЗ и логарифмы Вместе нужно записать!

8.

ЗАПОМНИ !
Сладкая
парочка!
Два
сапога –
пара!
Два в
одном
!
Логарифм и ОДЗ
ОНА
ОДЗ!
ОН
ЛОГАРИФМ!
вместе
трудятся
везде!
Два берега
у одной
реки!
Нам не жить
друг без
друга!
Близки и
неразлучны!

9.

Теперь полезность функции
мы четко обоснуем
И яркую картину нарисуем.
Вот вы когда-нибудь
слыхали
О логарифмической
спирали?

10. Закручены по ней рога козлов И не найдете вы на них узлов.

Моллюсков многих и улиток
Ракушки тоже все завиты.
И как сказал поэт великий Гете:
«Вы совершеннее строенья не найдете!»
И эту спираль мы повсюду встречаем:
К примеру, ножи в механизме вращая.
В изгибе трубы мы ее обнаружим –
Турбины тогда максимально послужат!

11. Наверняка, и о том вы не знали, Галактики тоже кружат по спирали!

В подсолнухе семечки тоже
закручены
И паука все плетенья заучены.
Наверняка, и о том вы
не знали,
Галактики тоже кружат
по спирали!

12.

Представление команд

13. Лови ошибку!

Понятия
Формулы
1.Определение логарифма числа
по заданному основанию
2. Основное логарифмическое
тождество.
log a a c c
log a b
log c b
1
; log a b
log c a
log b a
log a 1 0
3. Формула логарифм произведения.
4. Формула логарифм частного.
log a b log b a 1
5. Формула логарифм степени.
log a b n n log a b
6. Формула логарифмического перехода от
одного основания к другому основанию.
a
loga c
c
x1
log x1 log x2
x2
7. Логарифм, значение которого равно единице
log
8. Логарифм, значение которого равно нулю
log x1 x2 log x1 log x2
9. Запись числа через логарифм
log a b x b a x , a 0, a 1, b 0

14. Проверь себя!

Понятия
1.Определение логарифма числа по заданному
основанию
Формулы
log a b x b a x , a 0, a 1, b 0
2. Основное логарифмическое тождество.
3. Формула логарифм произведения.
4. Формула логарифм частного.
5. Формула логарифм степени.
6. Формула логарифмического перехода от
одного основания к другому основанию.
7. Логарифм, значение которого равно единице
8. Логарифм, значение которого равно нулю
9. Запись числа через логарифм
a
loga c
c
log x1 x2 log x1 log x2
log
x1
log x1 log x2
x2
log a b n n log a b
log a b
log c b
1
; log a b
log c a
log b a
log a a 1
log a 1 0
log a a c c

15.

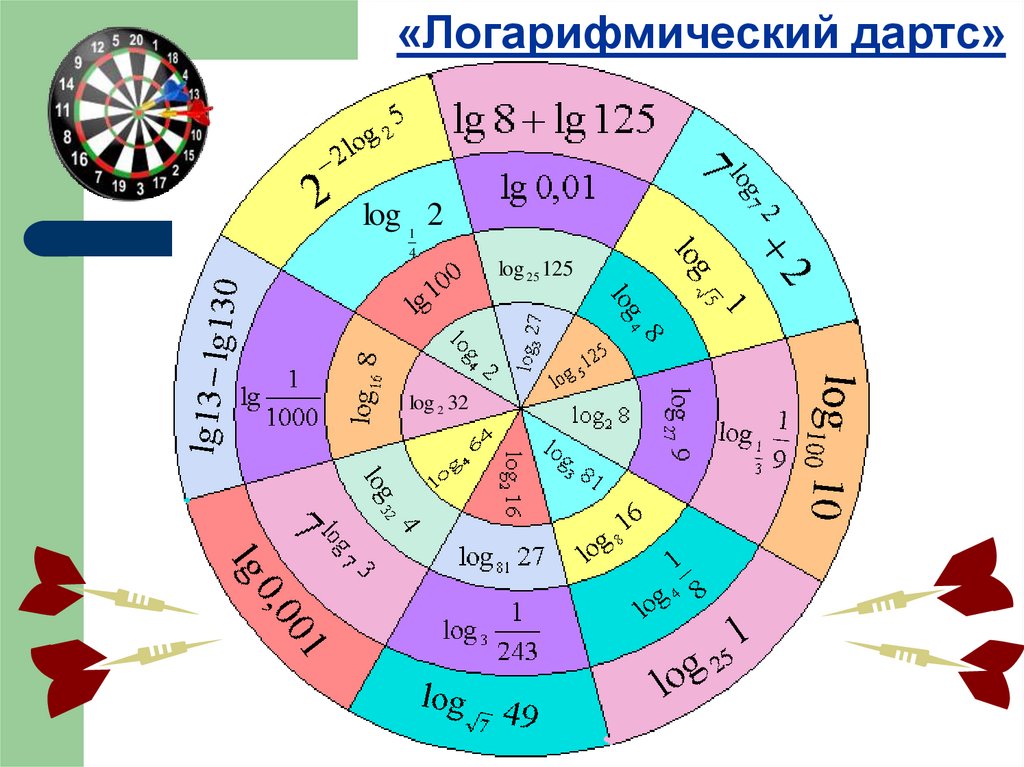
«Логарифмический дартс»
log 1 2
4
log 25 125
log 2 32

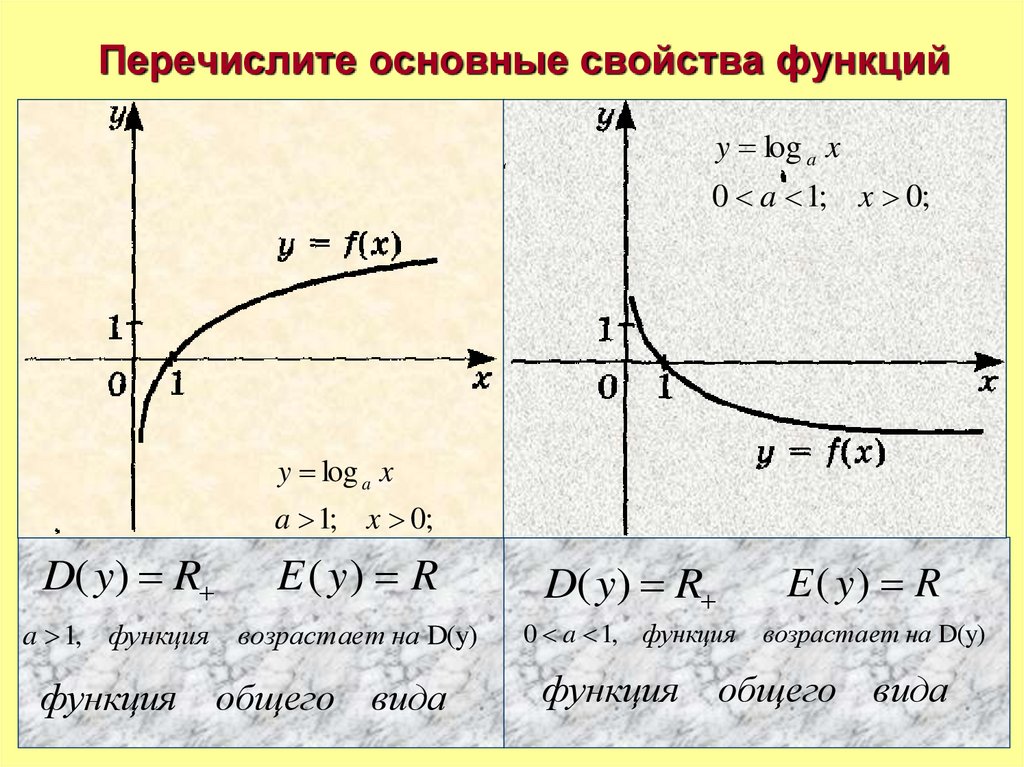
16. Перечислите основные свойства функций

y log a x
0 a 1; x 0;
y log a x
D( y) R
a 1; x 0;
D( y) R
a 1, функция
функция
E ( y) R
D( y) R
возрастает на D(y)
0 a 1, функция
общего вида
функция
E ( y) R
возрастает на D(y)
общего вида

17. Найти область определения функции

y log 0,5 (3 2 x)
3 2x 0
2 x 3
1) ( ; 1,5);
2x 3
2) ( ; 1,5);
3) (1,5; );
3
x
2
x 1,5
4) ( ;1,5]
1,5

18.

Очевидно, что ¼ > 1/8
После приведения
2
(½) >(½)
к основанию ½:
3
После логарифмирования
по основанию 10:
2
lg ( ½ ) > lg ( ½ )
3
По свойству логарифмов: 2 lg ( ½ ) > 3 lg ( ½ )
После сокращения на lg ( ½ ):
В чём ошибка?
2>3
2 > 3 ?!

19. Логарифмическая «комедия 2>3» Решение:

Логарифмическая «комедия 2>3»
Решение:
1
1
1
lg 0 2 lg 3 lg
2
2
2
2 3

20. Проба сил

Найти
2
значение выражения:
log2 7
2 log 5 15 log 5 9.
2
15
7 log 5
7 log 5 25 7 2 9.
9