Similar presentations:
Логарифмическая функция и ее свойства
1. "Логарифмическая функция и ее свойства"
"Логарифмическаяфункция и ее
свойства"
ГАОУ СПО «ККСД»
Преподаватель Филимонова Ольга
Николаевна
г. Калуга
2.
Есть в математике тема одна,Логарифмической функцией называется она,
Логарифм появился, чтобы легче считать,
Логарифм – ПОКАЗАТЕЛЬ,
Это надо знать!
Цель урока:
Обобщить и систематизировать знания о
свойствах логарифмической функции
3.
Использование свойствлогарифмической функции для
выполнения заданий с логарифмами
Сравнивать
выражения
Выполнять
преобразования
выражений
Выполнять
логарифмирование
и потенцирование
выражений
Решать
логарифмические
уравнения
Находить
значения
выражений
Строить графики
логарифмических
функций
Решать
алгебраические
неравенства
Решать
логарифмические
неравенства
4.
«Я старался,насколько мог и
умел, отделаться
от трудности и
скуки
вычислений,
докучность
которых обычно
отпугивает
весьма многих от
изучения
математики»
Джон Непер
(Шотландия, 17 век)
5. Из истории логарифмов
Слово логарифм происходит отгреческого λογοφ (число) и ρίνμοφ
(отношение) и переводится,
следовательно, как отношение чисел.
Выбор изобретателем (1594 г.)
логарифмов Джоном Непером такого
названия объясняется тем, что логарифмы
возникли при сопоставлении двух чисел,
одно из которых является членом
арифметической прогрессии, а другое –
геометрической.
6. Русский математик Аничков Д. С. о логарифмах
«Ежели под геометрическою прогрессиею,начинающеюся с единицы, подписана будет
арифметическая прогрессия, начинающаяся с нуля, то
числа, внизу подписанные, называются для верхних –
логарифмы.
Положим, что даны прогрессии:
геом.
1, 2, 4, 8, 16, 32, 64, 128, 256,
арифм.
0, 1, 2, 3, 4, 5, 6,
7,
Тогда логарифм 1 будет 0;
логарифм 4 будет 2;
а логарифм 32 будет 5 и проч.»
8.
7.
СТЕПЕНЬ1.
2.
3.
1.
2.
3.
Определения:
ап = х
(а > 0)
а0 = 1
(а ≠ 0)
а1 = а
Свойства:
а х . а у = а х+у
ах :ау = аx -y
( а х ) у = а ху
ЛОГАРИФМ
1.
2.
3.
1.
2.
3.
при а > 0, a ≠ 1,
x > 0, y > 0
Определения:
log a x = n <=> а п = х, т.е.
a log a x = x
log a 1 = 0
log a a = 1
Свойства:
log a ( x . y ) = log a x + log a y
log a x / y = log a x – log a y
log a x n
= n . log a x
8.
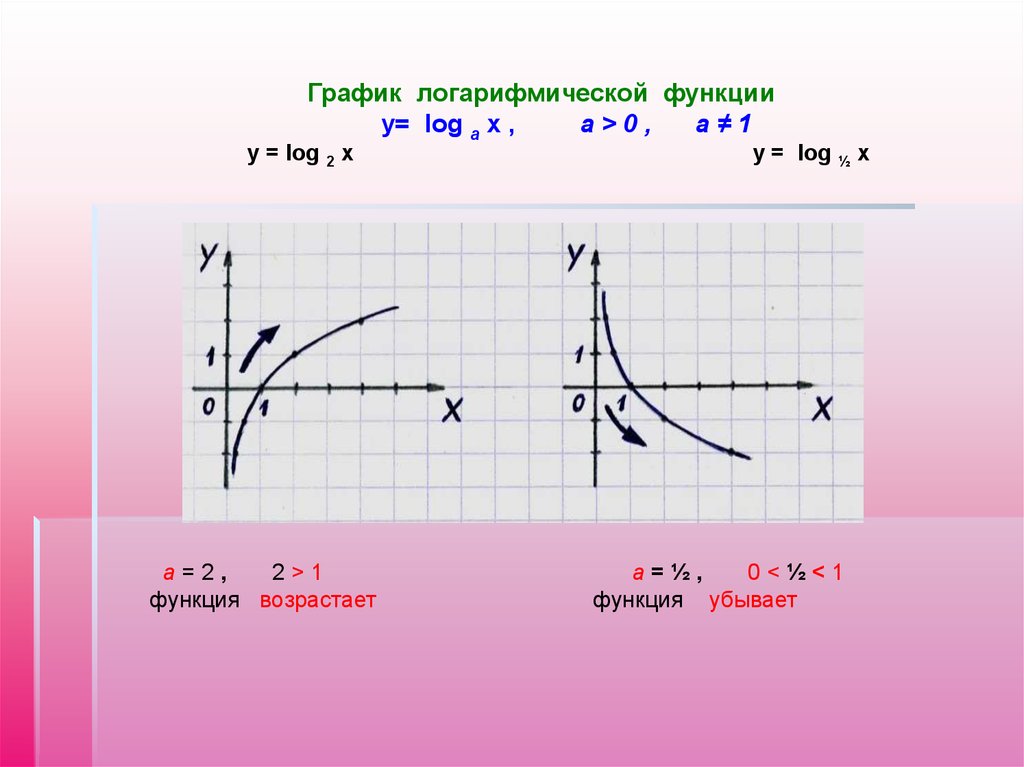
График логарифмической функцииу= log a x ,
a>0,
a≠1
y = log 2 x
а=2,
2>1
функция возрастает
y = log ½ x
a=½,
0<½<1
функция убывает
9.
Очевидно, что ¼ > 1/8После приведения
2
3
( ½ ) > ( ½ )
к основанию ½:
После логарифмирования
2
3
lg ( ½ ) > lg ( ½ )
по основанию 10:
По свойству логарифмов:
После сокращения на
2 lg ( ½ ) > 3 lg ( ½ )
lg ( ½ ):
2 > 3
В чём ошибка?
2 > 3 ?!
10.
ЗАПОМНИ !Сладкая
парочка!
Два
сапога –
пара!
Два в
одном!
Нам не жить
друг без
друга!
Логарифм и ОДЗ
вместе
трудятся
ОНА
ОДЗ!
ОН
ЛОГАРИФМ!
везде!
Два берега
у одной
реки!
Близки и
неразлучны!
11.
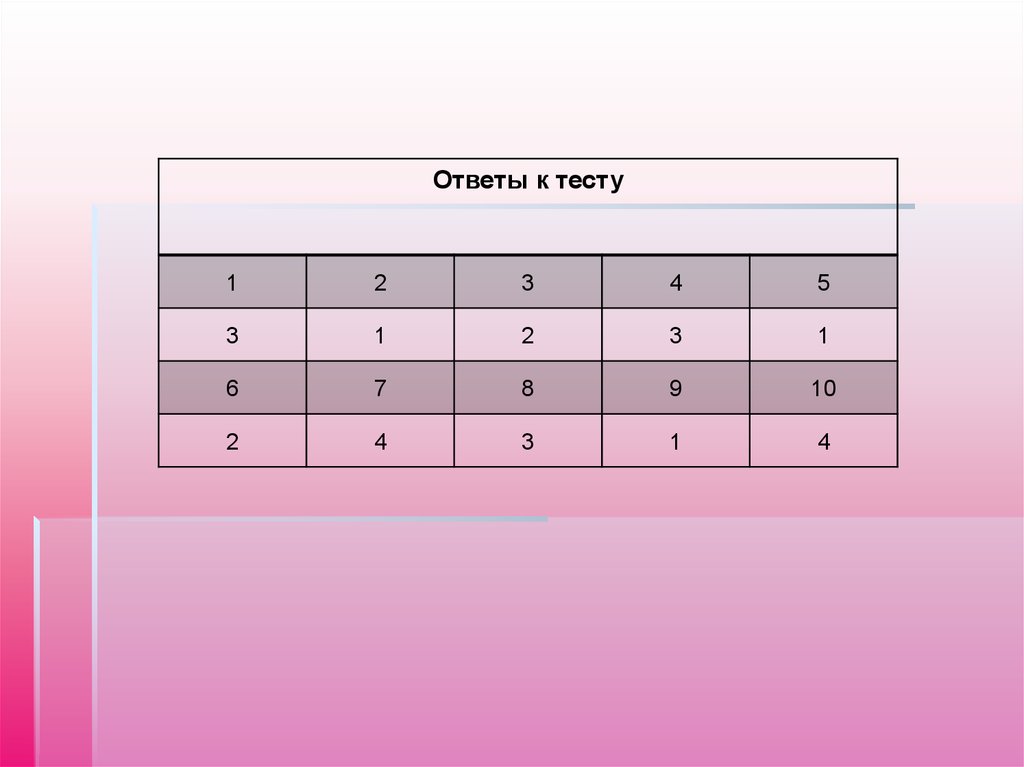
Ответы к тесту1
2
3
4
5
3
1
2
3
1
6
7
8
9
10
2
4
3
1
4
12.
Логарифмы в деятельности человекав электротехнике
в астрономии
в животноводстве
в технике
в экономике
в музыке
13. и в природе
семечки подсолнухапаутина
галактика
раковина
рога козла
14.
По горизонтали:1.Название члена при делении
2.Прямая, имеющая единственную общую точку с окружностью
3.Равенство двух отношений
4.Знак, меняющий значение выражения на противоположное
5.Член многочлена, имеющий только числовое значение
По вертикали:
1.Расстояние от начала отсчета до точки, изображающей число
2.Ось координатной плоскости
3.Множество точек (Х; f (Х) ) на плоскости
4.Действие, определяющее сумму
5.Тригонометрическая функция
15. Значимость логарифмов
«С точки зрения вычислительнойпрактики, изобретение логарифмов по
важности можно смело поставить рядом с
другим, более древним великим
изобретением индусов – нашей десятичной
системой нумерации.»
Успенский Я. В.,
русский математик










 mathematics
mathematics








