Чтение графика функции

1. Чтение графика функции

Описание свойств функции с
помощью графика

2.

3.

Схема исследования функции:
Область определения функции.
Наибольшее, наименьшее значения
функции
Непрерывность.
Нули функции.
Промежутки знакопостоянства.
Промежутки возрастания, убывания
функции.
Множество значений функции.

4.

5. Все значения, которые принимает независимая переменная (аргумент), образуют область определения функции.

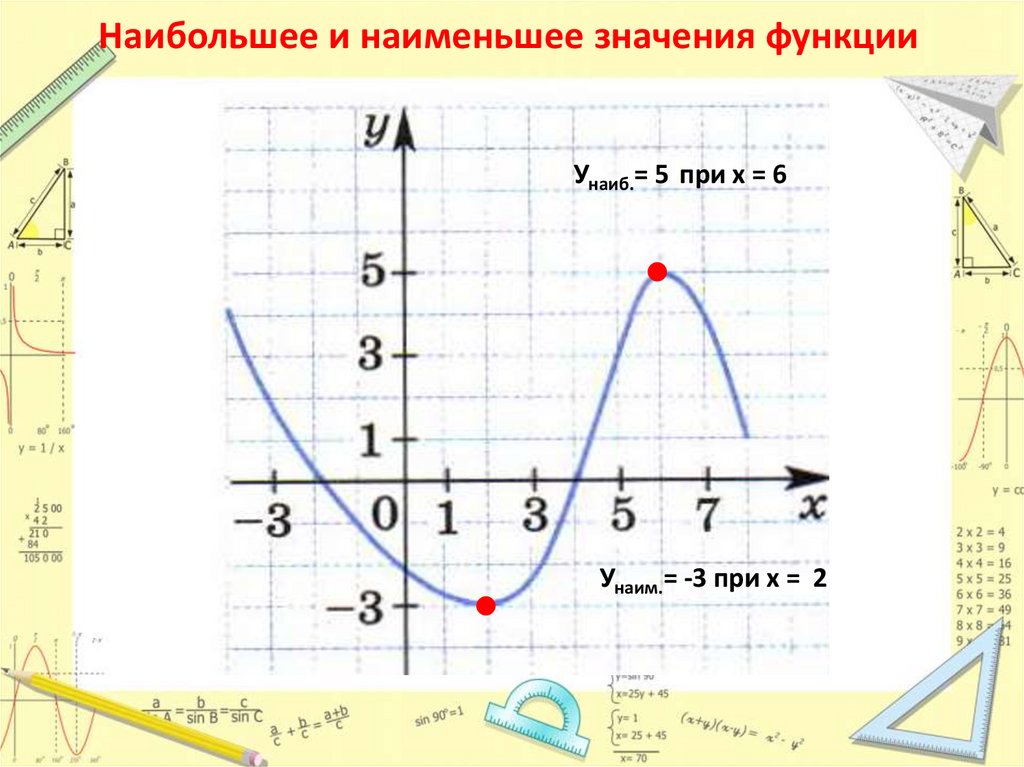
D(f)=[ -4; 8]

6. Наибольшее и наименьшее значения функции

Унаиб.= 5 при х = 6
Унаим.= -3 при х = 2

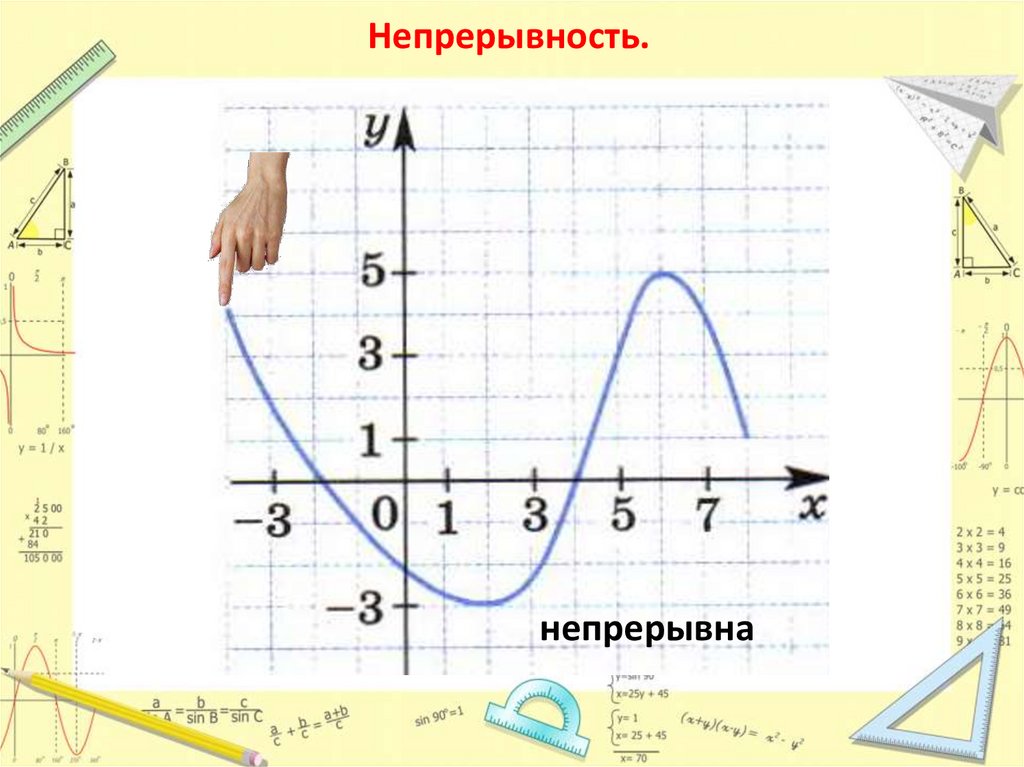
7. Непрерывность.

непрерывна

8. Графический нуль функции – это абсцисса точки пересечения графика функции с осью абсцисс.

У =0, если х = -2 и х = 4.

9. Промежутки знакопостоянства - это промежутки, на которых функция сохраняет (не меняет) знак. .

У>0, если x [-4;-2) и (4;8]
У<0, если x (-2;4)
-4
-2
4
8

10. Промежутки возрастания и убывания функции.

Убывает на отрезке [-4;2] и на
отрезке [6;8]
Возрастает на отрезке [2;6]

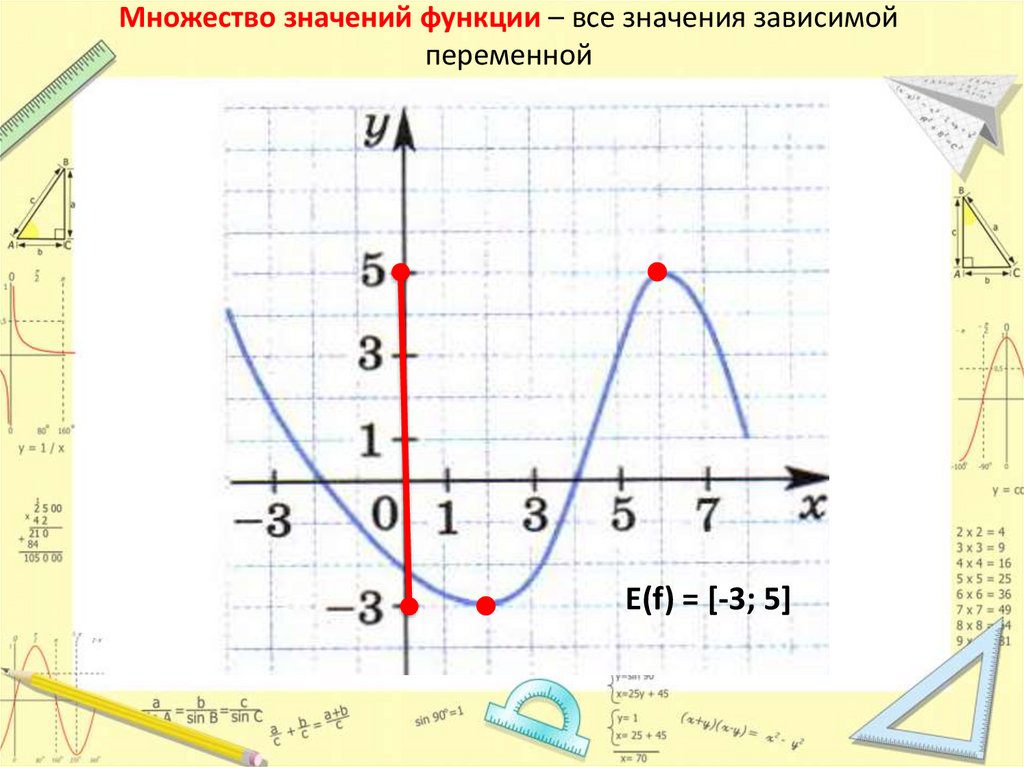
11. Множество значений функции – все значения зависимой переменной

E(f) = [-3; 5]

12. Прочитайте график функции

13.

1.D(f) = 5 ; 4 .
2. yнаиб.= 3
при х = 2
yнаим.= -2,5
при х = -1 и х = -5
3. Функция непрерывна
4. у =0 при х = -4; -2;0; 3; 4.
5. y>0 при x 4 ; 2 и 0 ;3 ,
y<0 при x 5; 4 и 2 ;0 и 3; 4 .
6. функция возрастаетна 5 ; 3 , на 1;2 и на 3,5 ; 4
функция убывает на 3 ; 1 и на 2;3,5 .
7. E(f) = 2,5 ; 3 .