Similar presentations:
Треугольные призмы. Урок № 41
1.
Урок № 41ПРИЗМЫ
ПЛАН УРОКА:
1 Устно разбираемся с теорией
2 Письменно решаем задачи
3 Записываем ДЗ
2.
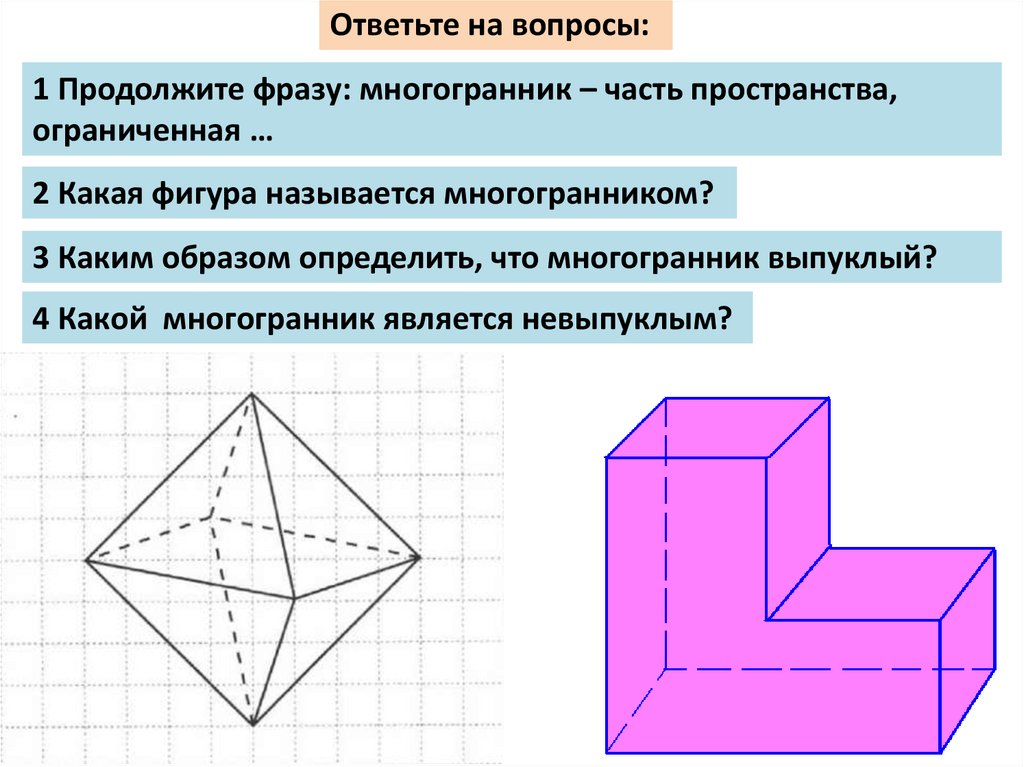
Ответьте на вопросы:1 Продолжите фразу: многогранник – часть пространства,
ограниченная …
2 Какая фигура называется многогранником?
3 Каким образом определить, что многогранник выпуклый?
4 Какой многогранник является невыпуклым?
3.
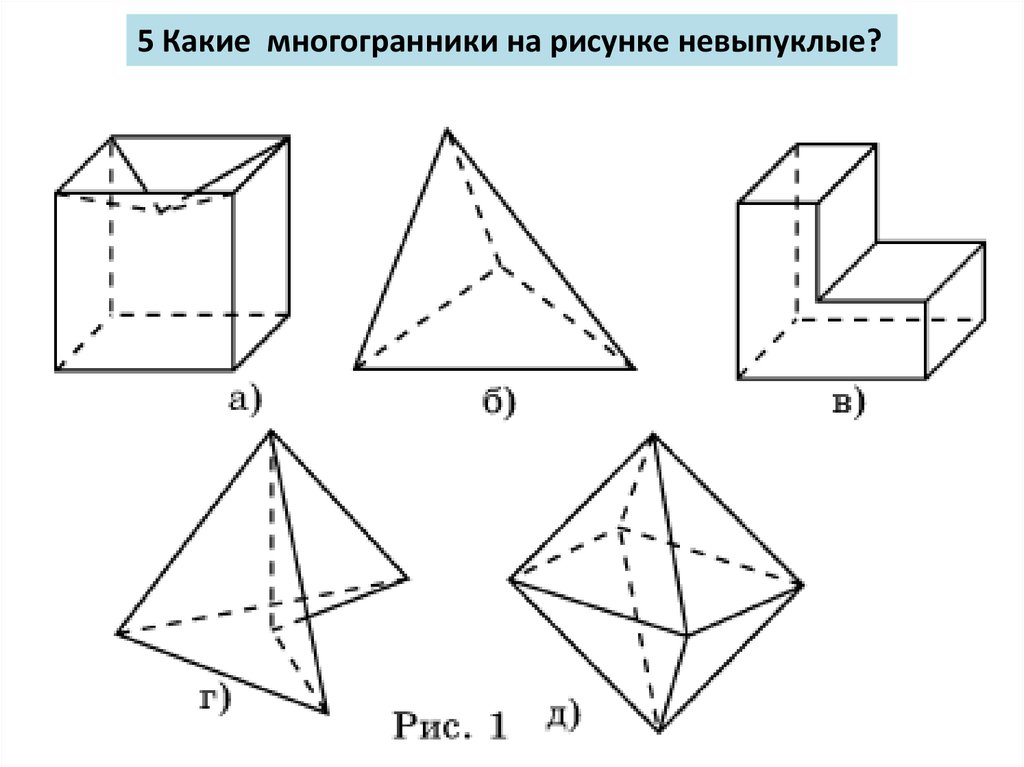
5 Какие многогранники на рисунке невыпуклые?4.
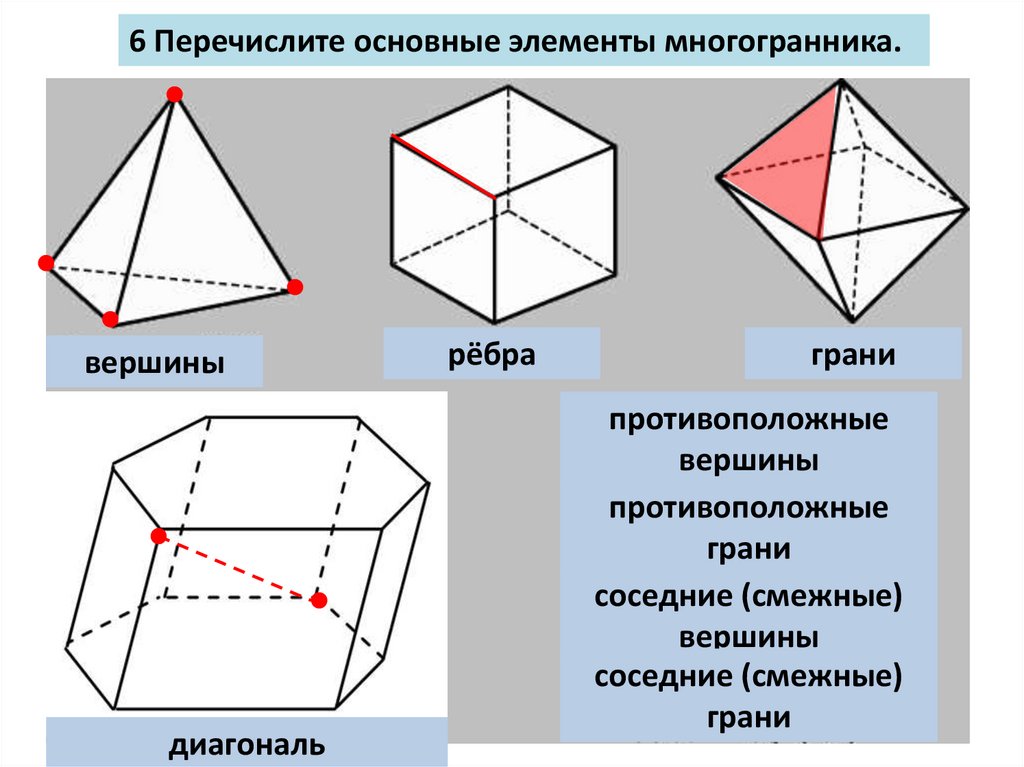
6 Перечислите основные элементы многогранника.вершины
диагональ
рёбра
грани
противоположные
вершины
противоположные
грани
соседние (смежные)
вершины
соседние (смежные)
грани
5.
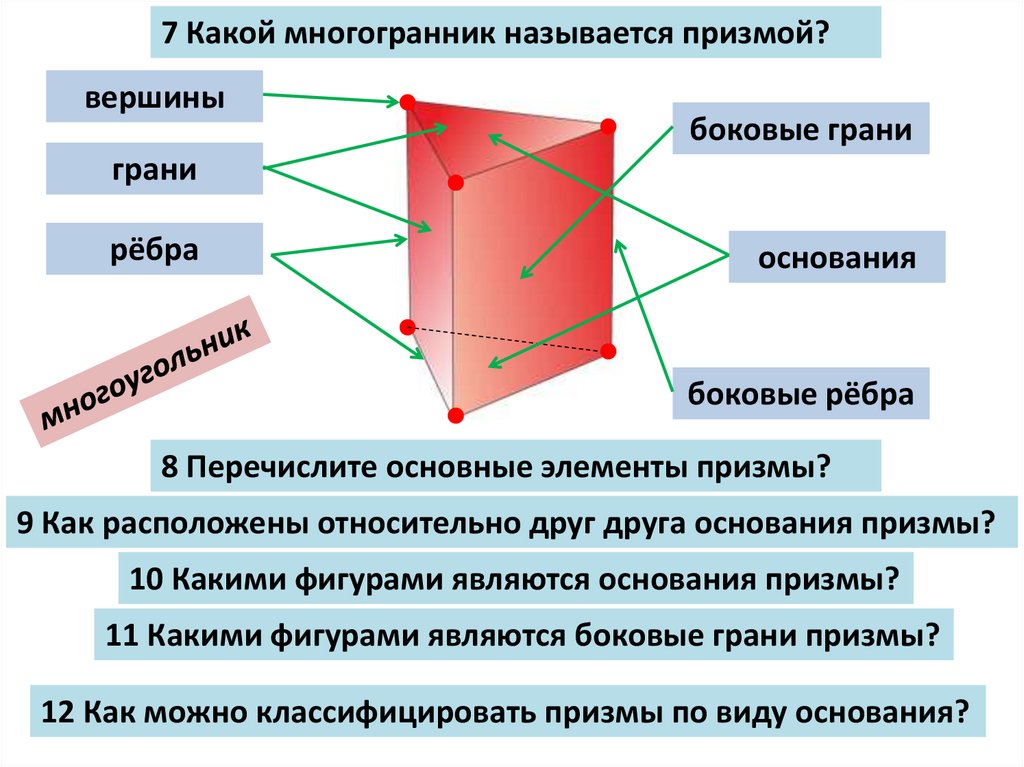
7 Какой многогранник называется призмой?вершины
боковые грани
грани
рёбра
основания
боковые рёбра
8 Перечислите основные элементы призмы?
9 Как расположены относительно друг друга основания призмы?
10 Какими фигурами являются основания призмы?
11 Какими фигурами являются боковые грани призмы?
12 Как можно классифицировать призмы по виду основания?
6.
C1B1
Н
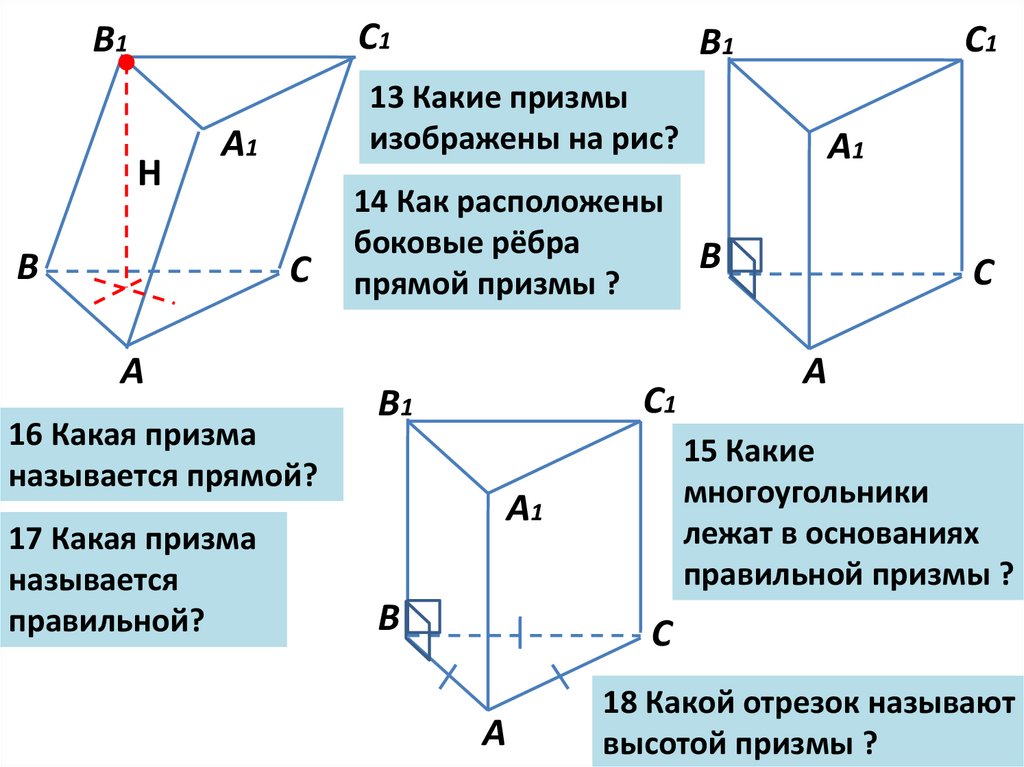
13 Какие призмы
изображены на рис?
А1
В
С
А
16 Какая призма
называется прямой?
17 Какая призма
называется
правильной?
C1
B1
14 Как расположены
боковые рёбра
прямой призмы ?
C1
B1
В
С
А
15 Какие
многоугольники
лежат в основаниях
правильной призмы ?
А1
В
А1
С
А
18 Какой отрезок называют
высотой призмы ?
7.
19 Расскажите по данным формулам: какая величинанаходится, что для этого необходимо знать?
V Sосн H
S
S ab
1
S ab
2
20 Решите задачу
a
2
4
3
1
S ah
2
1
S ab sin
2
S полн Sбок 2Sосн
8.
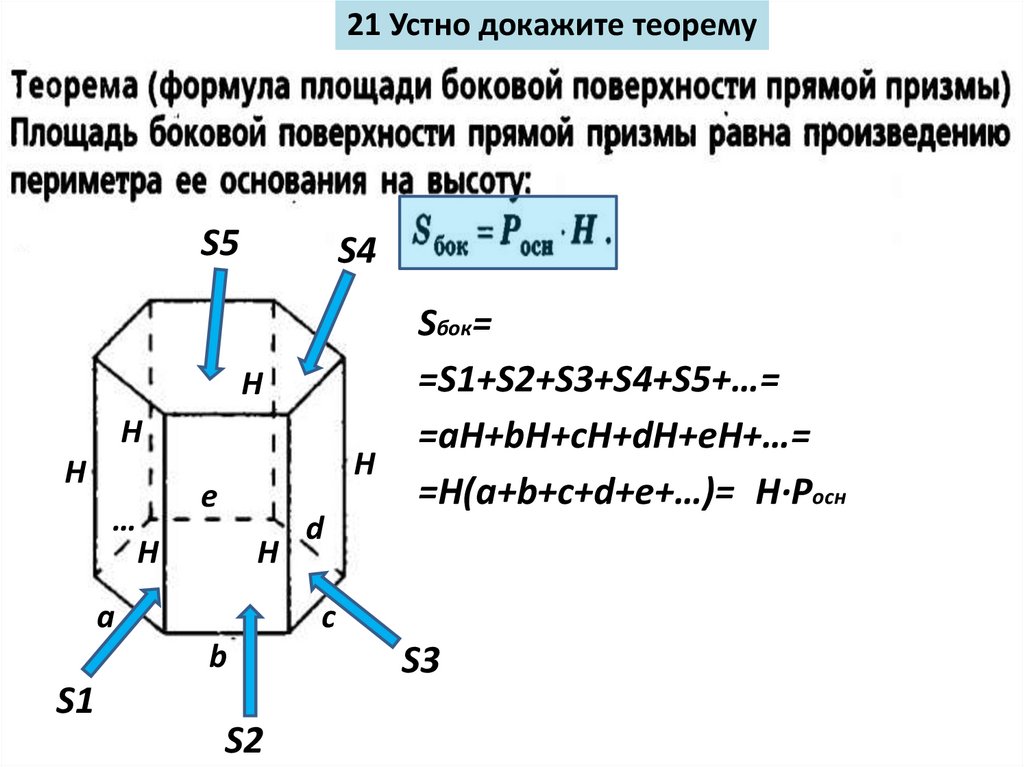
21 Устно докажите теоремуS5
S4
H
H
H
…
H
H
e
H
а
d
Sбок=
=S1+S2+S3+S4+S5+…=
=aH+bH+cH+dH+eH+…=
=H(a+b+c+d+e+…)= H∙Pосн
c
b
S1
S2
S3
9.
Решите задачи:1 В основании прямой призмы лежит прямоугольный
треугольник с катетами 12 и 16. Найдите площадь полной
поверхности и объём призмы, если боковое ребро равно 7.
2 В основании прямой призмы лежит равнобедренный
треугольник со сторонами 15, 15 и 18. Найдите площадь полной
поверхности и объём призмы, если боковое ребро равно 5.
3 Найдите площадь полной поверхности и объём прямой
призмы, если в основании призмы лежит треугольник у
которого две стороны равны 16 и 5, а угол между ними 120⁰.
Высота призмы равна 10.
4 Сторона основания правильной треугольной призмы равна 4.
Найдите площадь полной поверхности и объём призмы, если
боковое ребро равно 2√3.
10.
5 В правильной призме АВСА1В1С1 диагональ боковой граниравна 39. Найдите площадь полной поверхности и объём
призмы, если боковое ребро равно 36.
6 В основании прямой призмы АВСА1В1С1 лежит прямоугольный
треугольник с катетами 8 и 15. Найдите площадь полной
поверхности и объём призмы, если расстояние между
основаниями равно 8.
Задачу № 7 решим устно по построенному чертежу,
дома записать решение в тетрадь
7
11.
45
3
6
СС1=Х
2 Строим В1Х
3 Строим MN
В1Х
СВ=N
4 MNВ1А1 – искомое сечение
5
3
А1М
U
6
1 Строим А1М
U
7
5 Р(MNB1A1)=MN+NB1+B1A1+A1M
6 B1A1=6
N
7 ΔA1AM - прямоугольный
по теореме Пифагора A1M=5
8 MN ΙΙ А1В1
MN ΙΙ АВ
MN – средняя линия ΔАВС MN=3
Ответ: 19.
X
9 СN=NB по теореме Фалеса
10 ΔA1AM = ΔВ1ВN по 2 катетам
NB1=5
11 Р(MNB1A1)=19
12.
Домашнее задание № 41:повторить теорию, формулы.
1 В основании прямой призмы лежит прямоугольный
треугольник с катетами 9 и 40. Найдите площадь полной
поверхности и объём призмы, если боковое ребро равно 3.
2 В основании прямой призмы лежит равнобедренный
треугольник со сторонами 61, 61 и 120. Найдите площадь
полной поверхности и объём призмы, если боковое ребро
равно 4.
3 Найдите площадь полной поверхности и объём прямой
призмы, если в основании призмы лежит треугольник у
которого две стороны равны 3 и 5, а угол между ними 120⁰.
Высота призмы равна 1.
4 Сторона основания правильной треугольной призмы равна 6.
Найдите площадь полной поверхности и объём призмы, если
боковое ребро равно 3√3.
13.
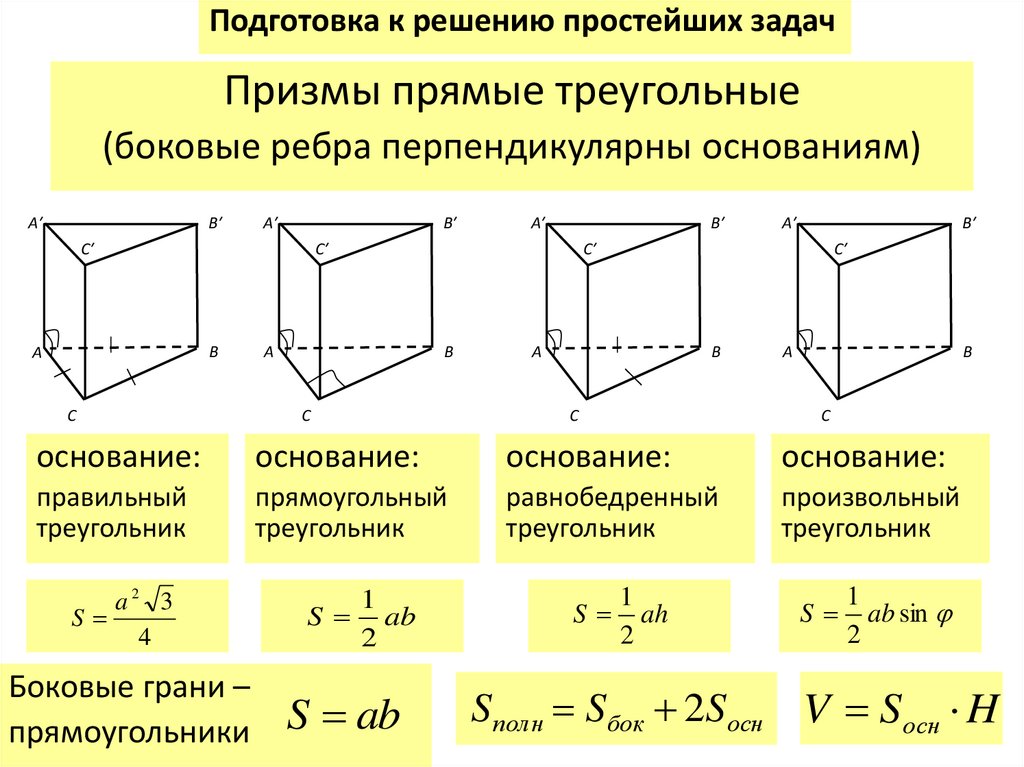
Подготовка к решению простейших задачПризмы прямые треугольные
(боковые ребра перпендикулярны основаниям)
А′
В′
А′
В′
С′
В′
С′
В
А
А′
С
А′
В′
С′
А
В
С
С′
А
В
А
В
С
С
основание:
основание:
основание:
основание:
правильный
треугольник
прямоугольный
треугольник
равнобедренный
треугольник
произвольный
треугольник
a2 3
S
4
S
Боковые грани –
прямоугольники
S ab
1
ab
2
S
1
ah
2
S
1
ab sin
2
S полн Sбок 2Sосн V Sосн H






 mathematics
mathematics








