Понятие многогранника. Призма

1.

2.

3.

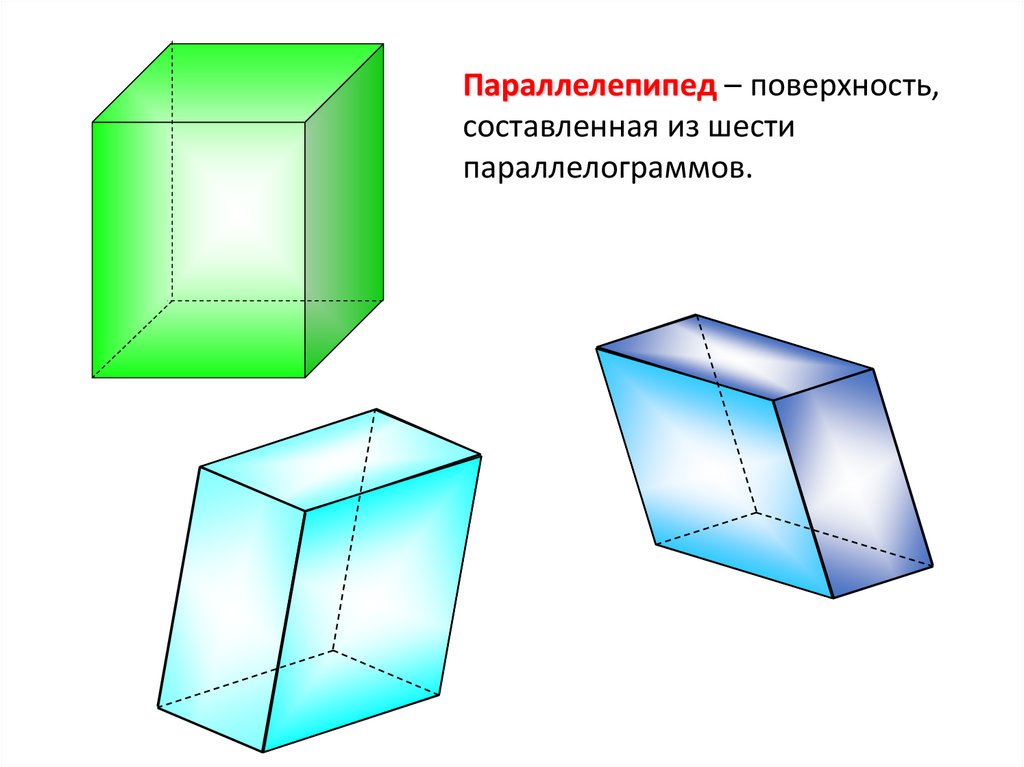
Параллелепипед – поверхность,
составленная из шести
параллелограммов.

4.

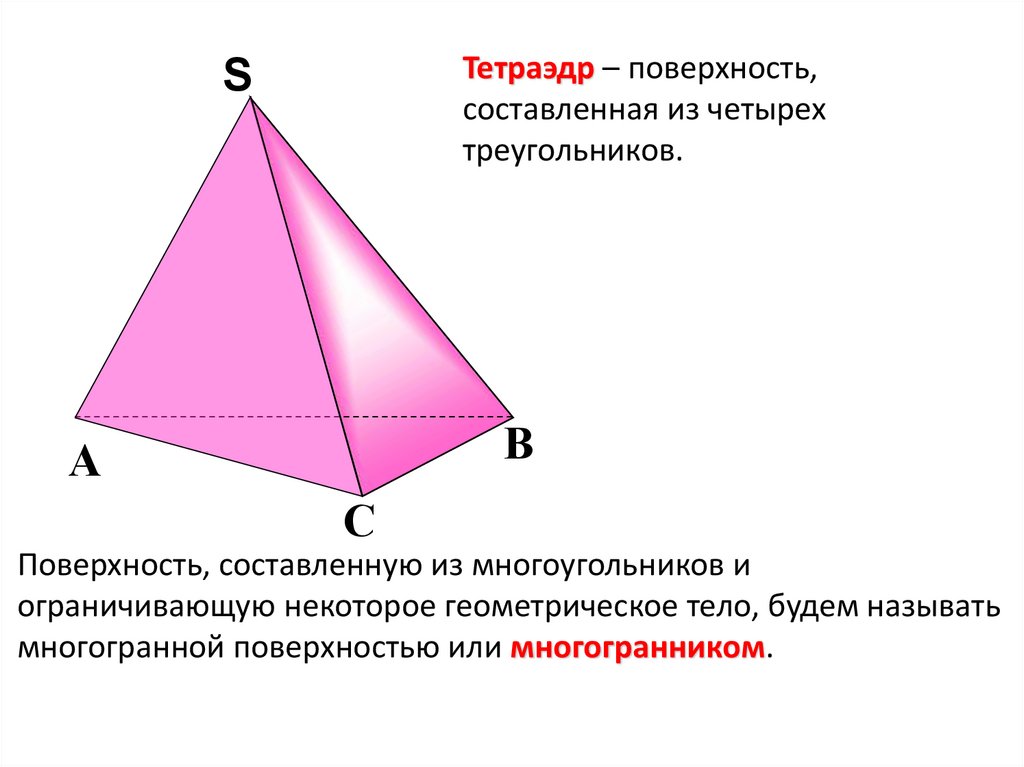
Тетраэдр – поверхность,
составленная из четырех
треугольников.
SS
В
А
С
Поверхность, составленную из многоугольников и
ограничивающую некоторое геометрическое тело, будем называть
многогранной поверхностью или многогранником.

5.

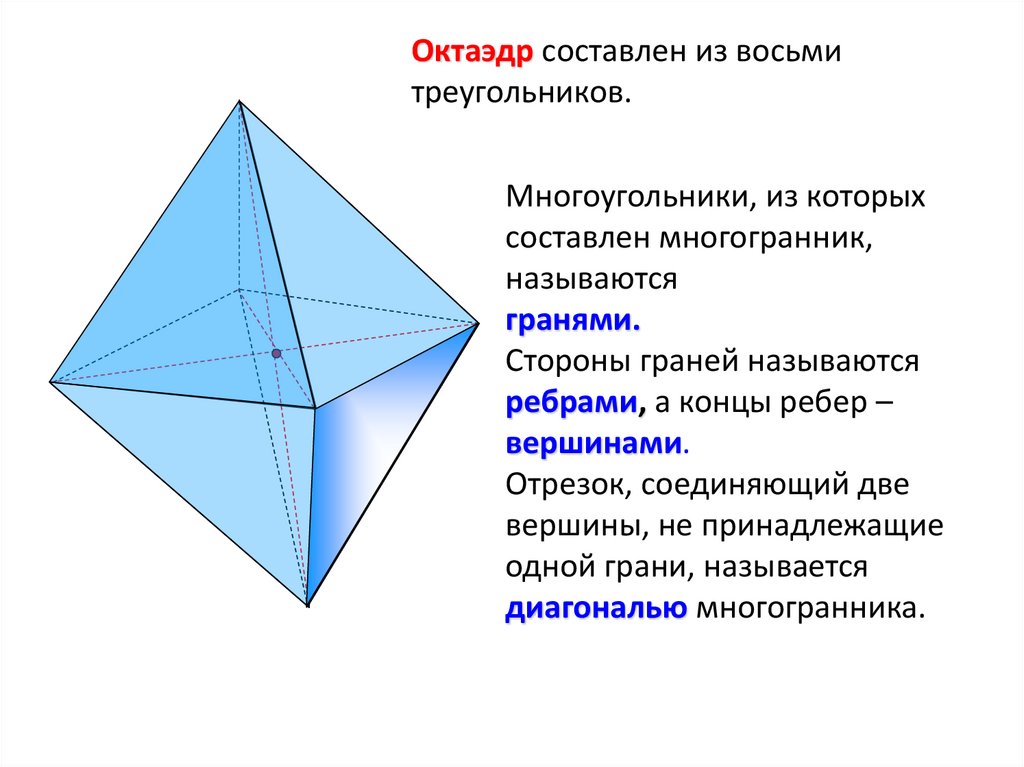
Октаэдр составлен из восьми
треугольников.
Многоугольники, из которых
составлен многогранник,
называются
гранями.
Стороны граней называются
ребрами, а концы ребер –
вершинами.
Отрезок, соединяющий две
вершины, не принадлежащие
одной грани, называется
диагональю многогранника.

6.

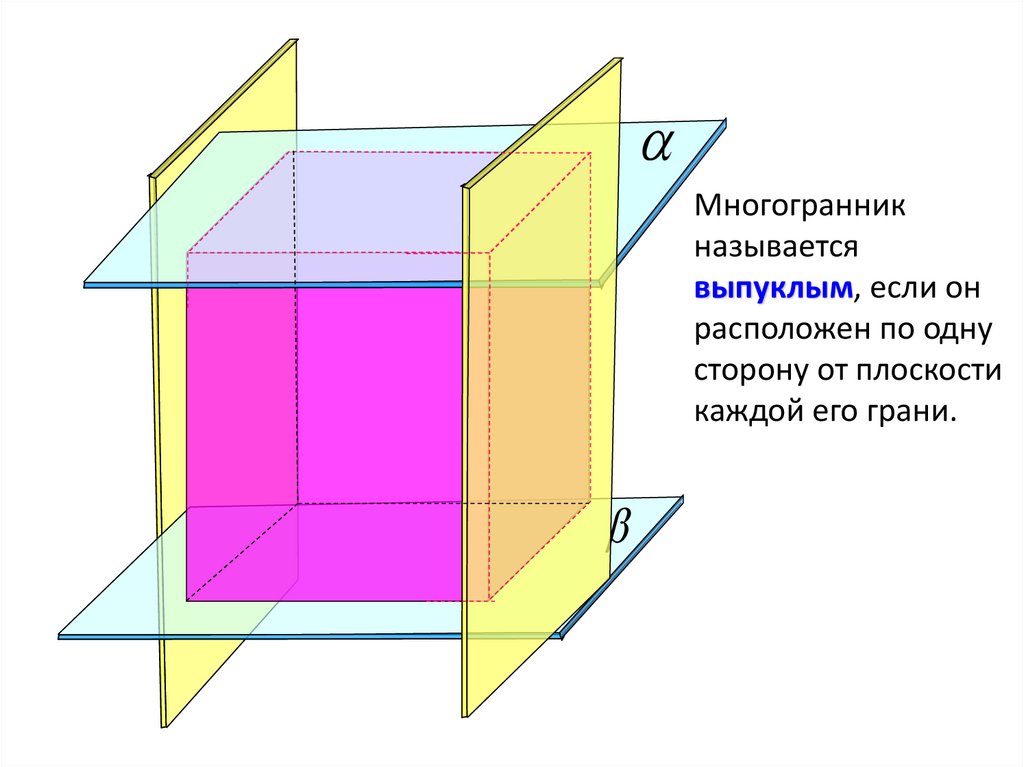
Многогранник
называется
выпуклым, если он
расположен по одну
сторону от плоскости
каждой его грани.

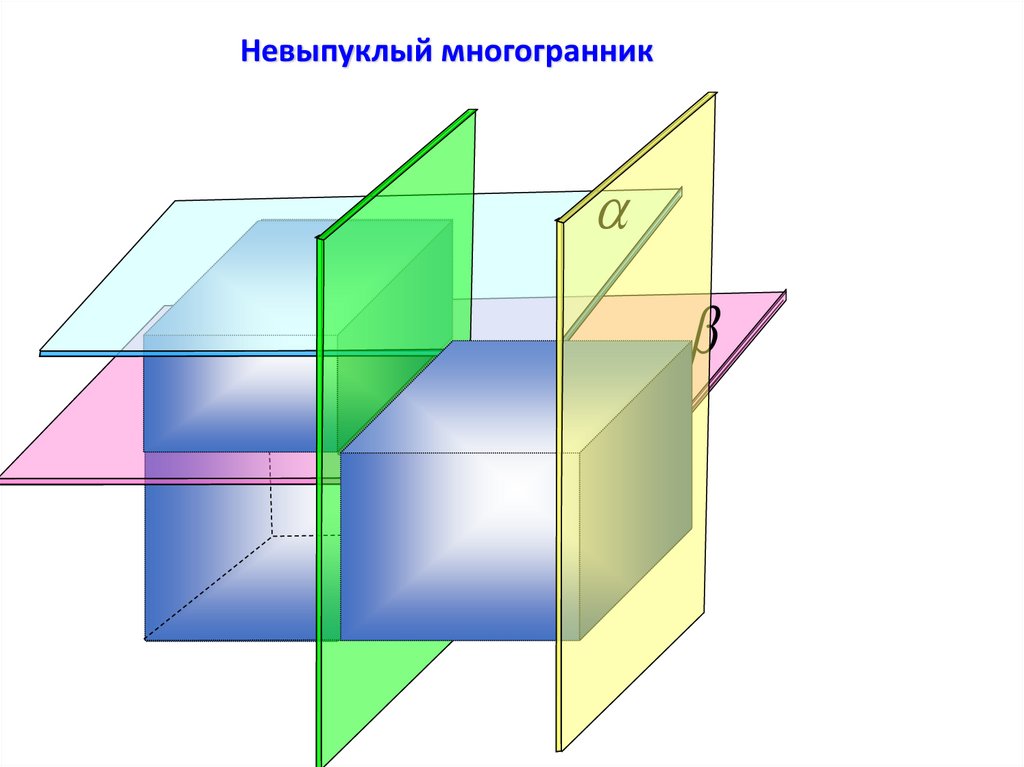
7.

Невыпуклый многогранник

8.

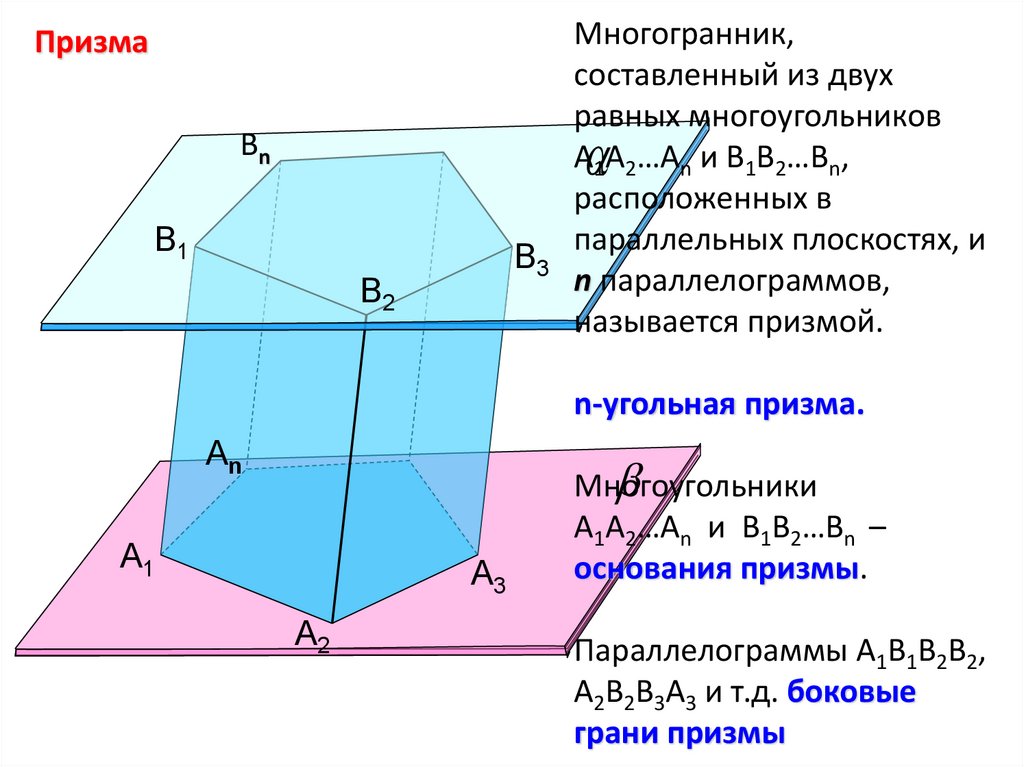
Призма
Многогранник,
составленный из двух
равных многоугольников
А1А2…Аn и В1В2…Вn,
расположенных в
параллельных плоскостях, и
n параллелограммов,
называется призмой.
Bn
B1
B3
B2
n-угольная призма.
Аn
А1
А3
А2
Многоугольники
А1А2…Аn и В1В2…Вn –
основания призмы.
Параллелограммы А1В1В2В2,
А2В2В3А3 и т.д. боковые
грани призмы

9.

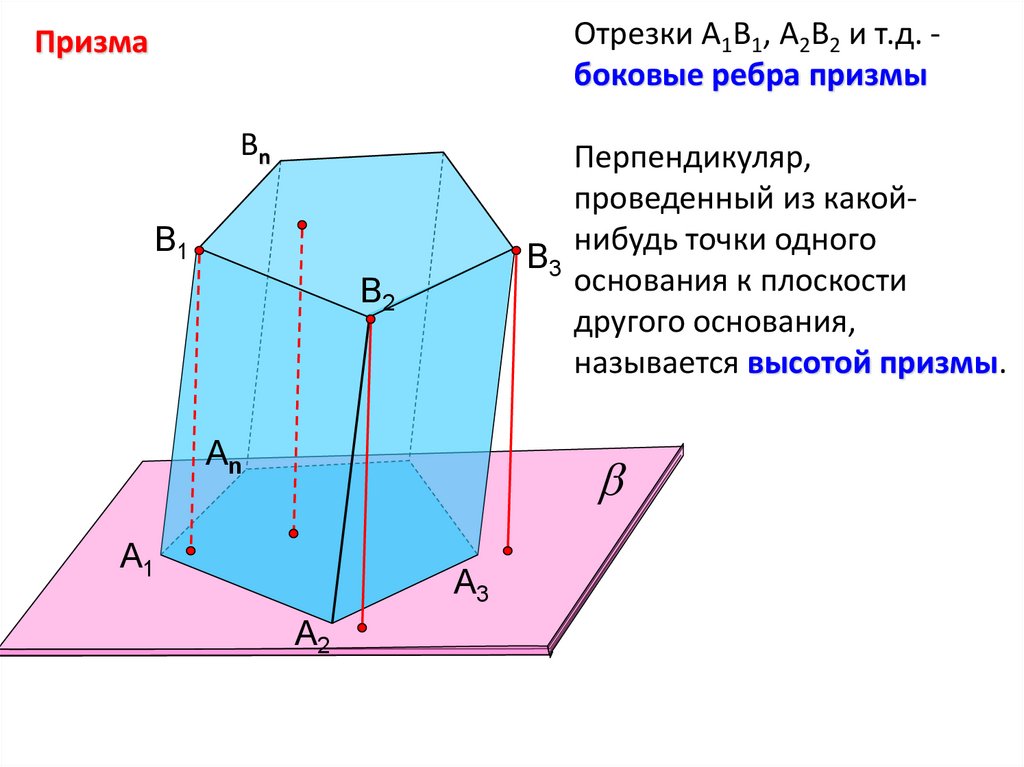
Отрезки А1В1, А2В2 и т.д. боковые ребра призмы
Призма
Bn
Перпендикуляр,
проведенный из какойнибудь точки одного
B3
основания к плоскости
другого основания,
называется высотой призмы.
B1
B2
Аn
А1
А3
А2

10.

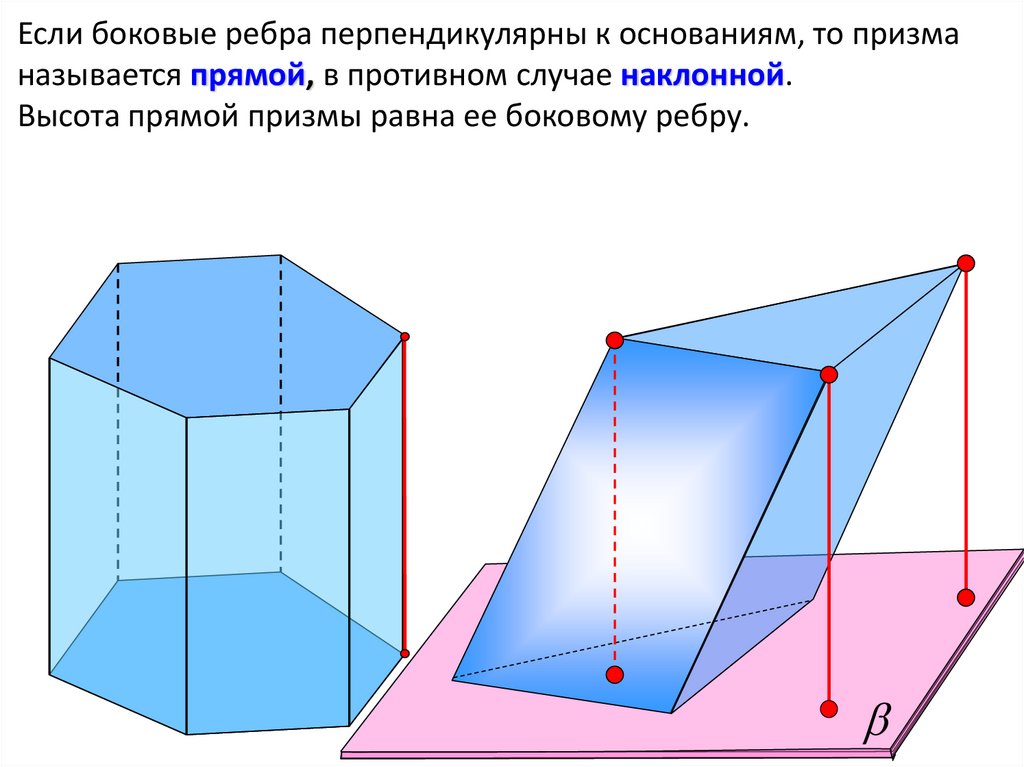
Если боковые ребра перпендикулярны к основаниям, то призма
называется прямой, в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.

11.

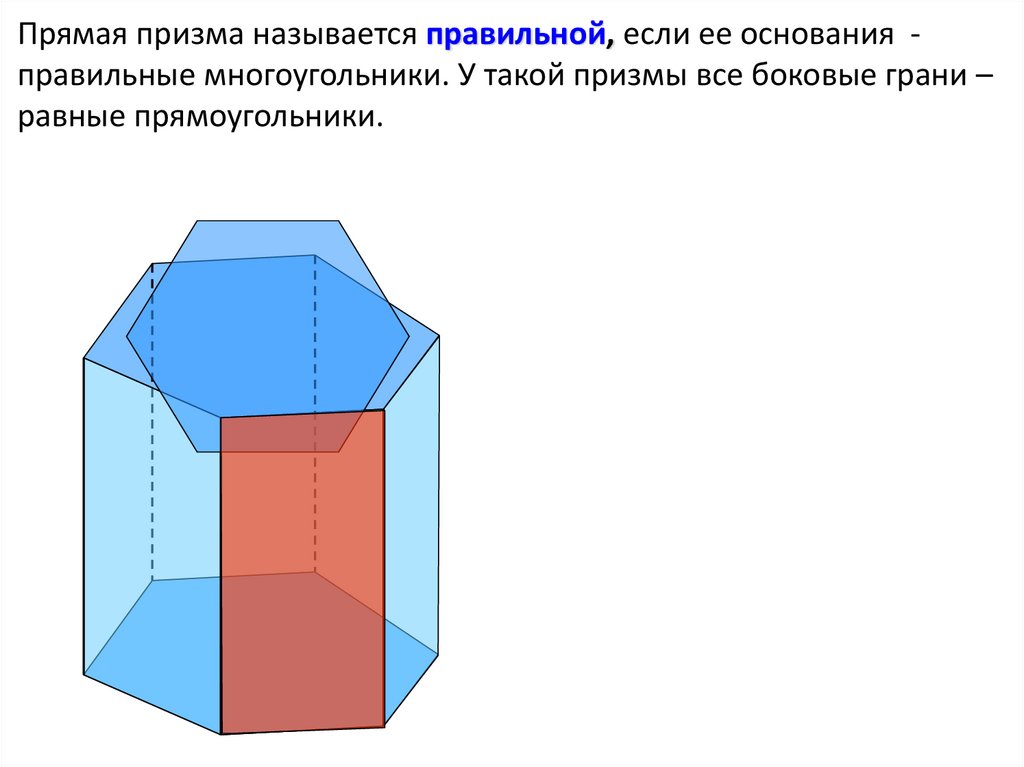
Прямая призма называется правильной, если ее основания правильные многоугольники. У такой призмы все боковые грани –
равные прямоугольники.

12.

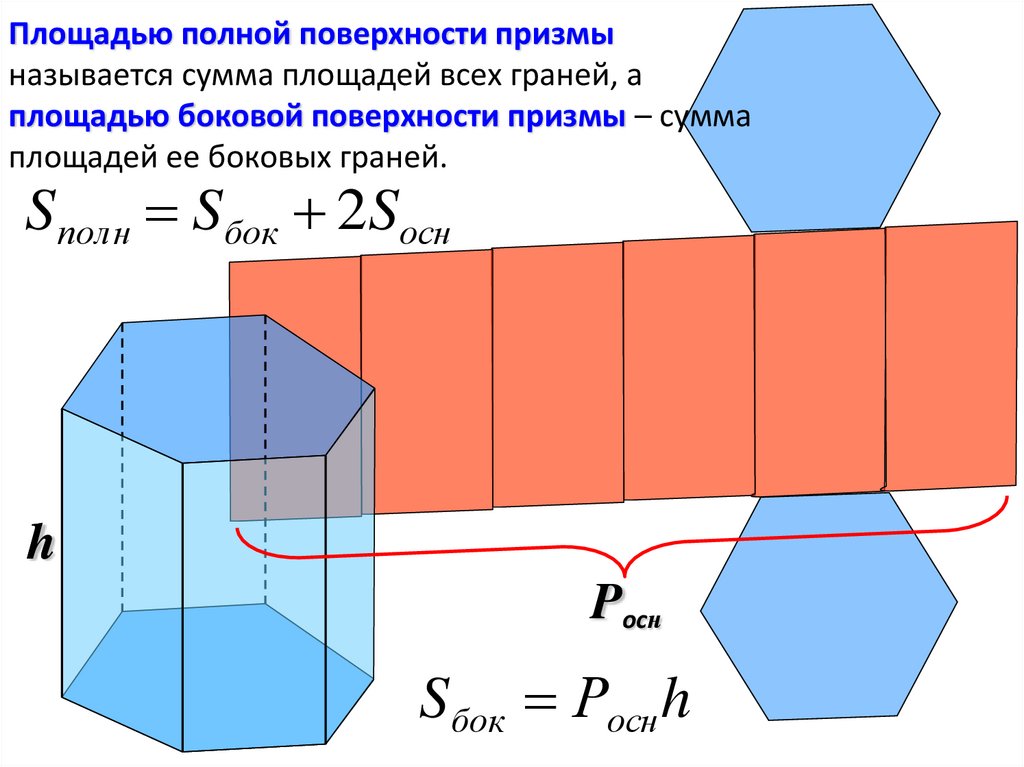
Площадью полной поверхности призмы
называется сумма площадей всех граней, а
площадью боковой поверхности призмы – сумма
площадей ее боковых граней.
Sполн Sбок 2Sосн
h
Pocн
Sбок Росн h

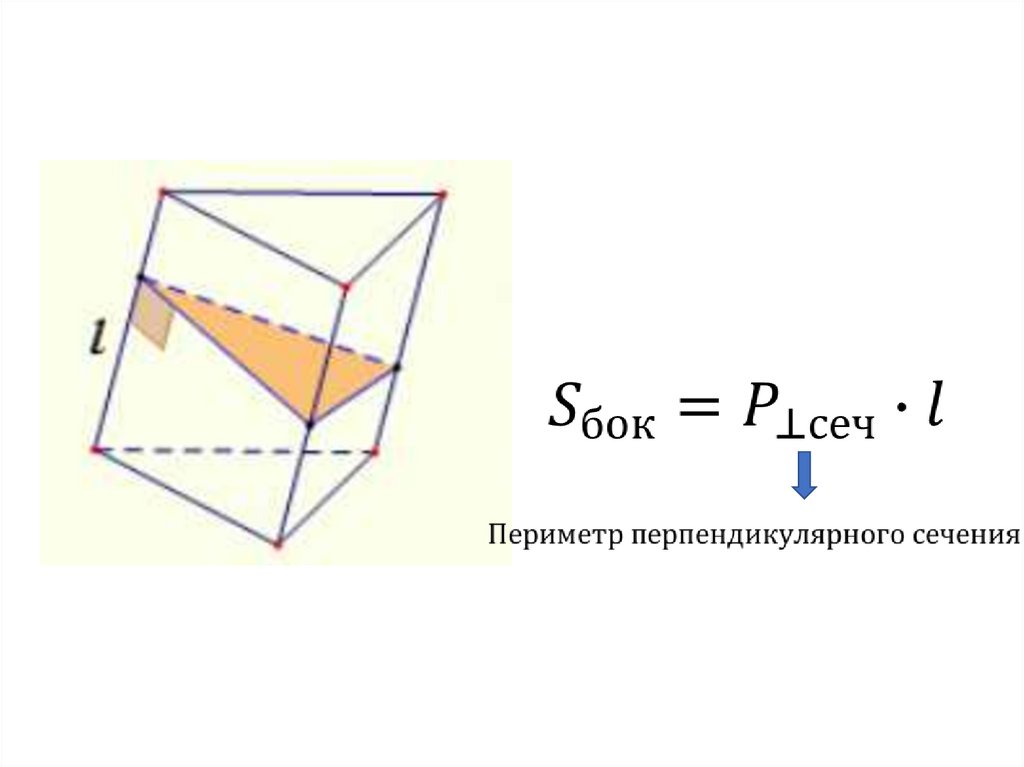
13.

Докажите, что площадь боковой поверхности
наклонной призмы равна произведению периметра
перпендикулярного сечения на боковое ребро.
S1=A1A2* l
S2=A2A3* l
+ S =A A * l
3
A4
A1
l
3 4
S4=A4A1* l
Sбок Рсеч l
l
A2
A3

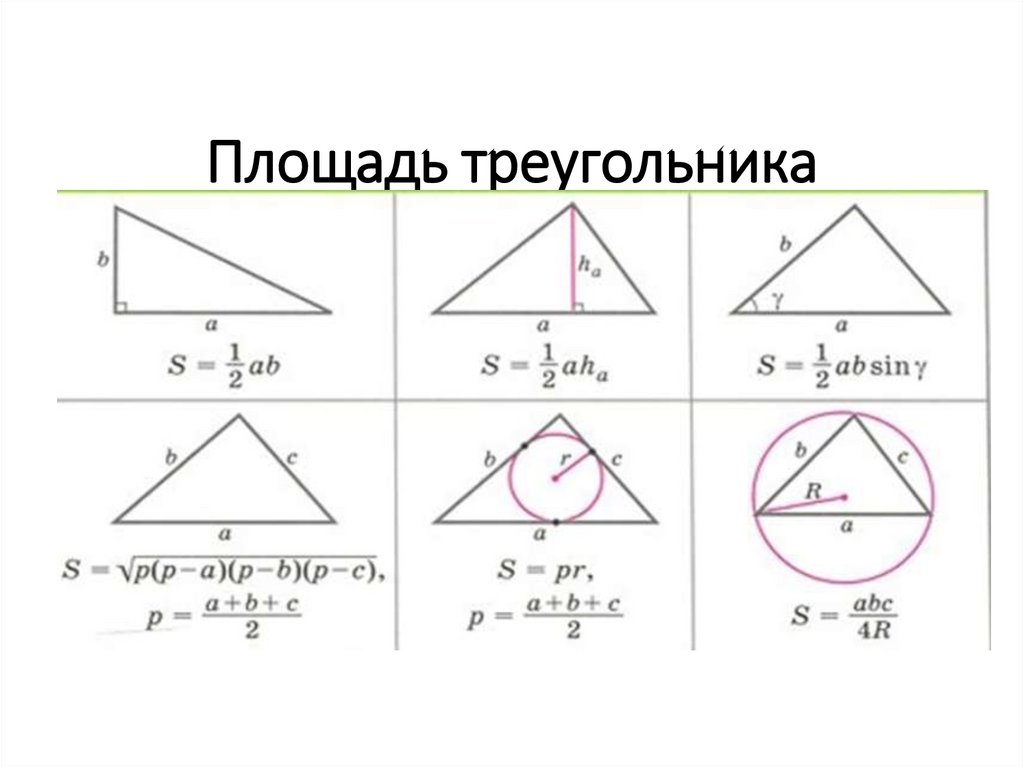
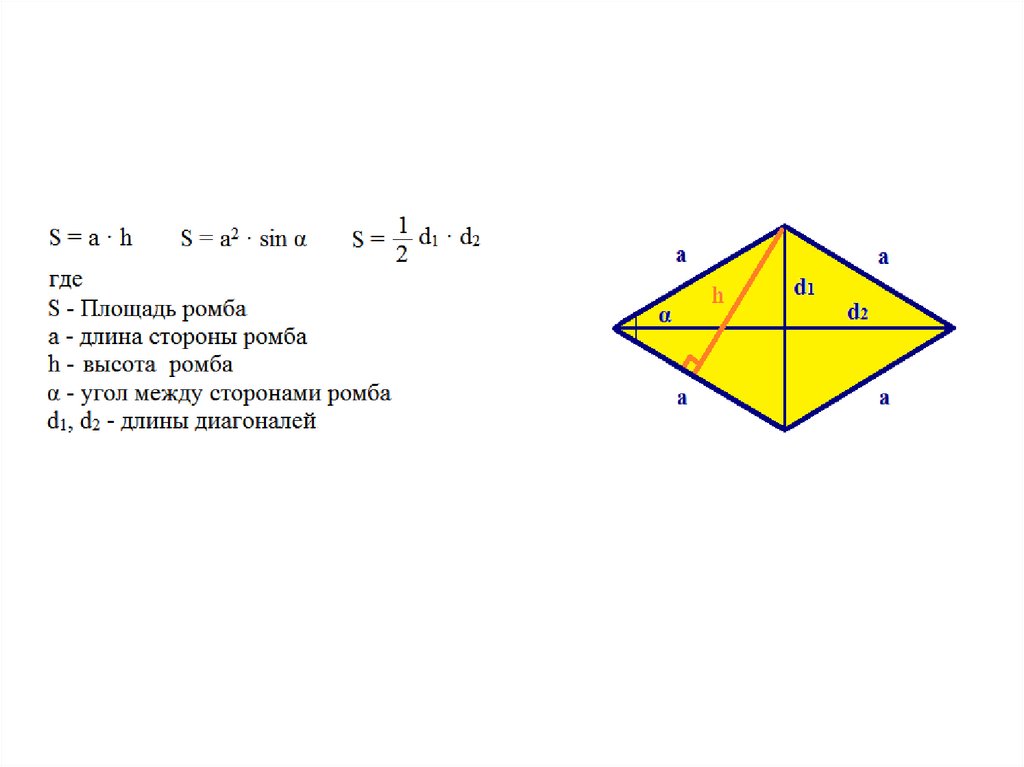
14. Площадь треугольника

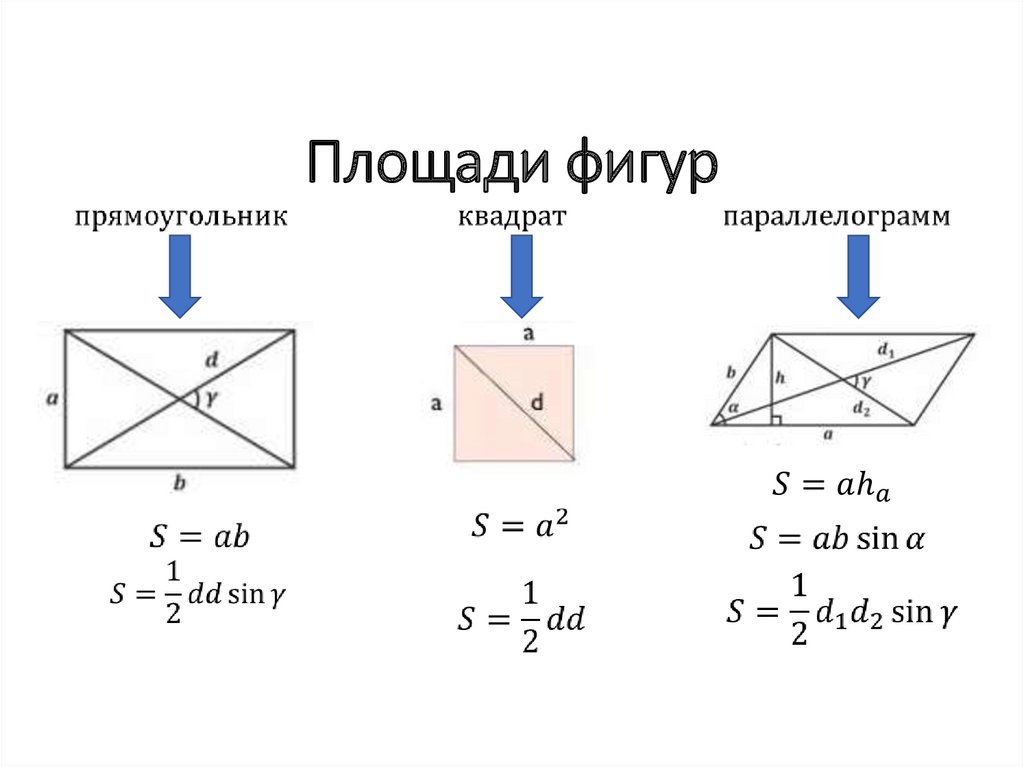
15. Площади фигур

16.

17. Площадь трапеции

18.

19.

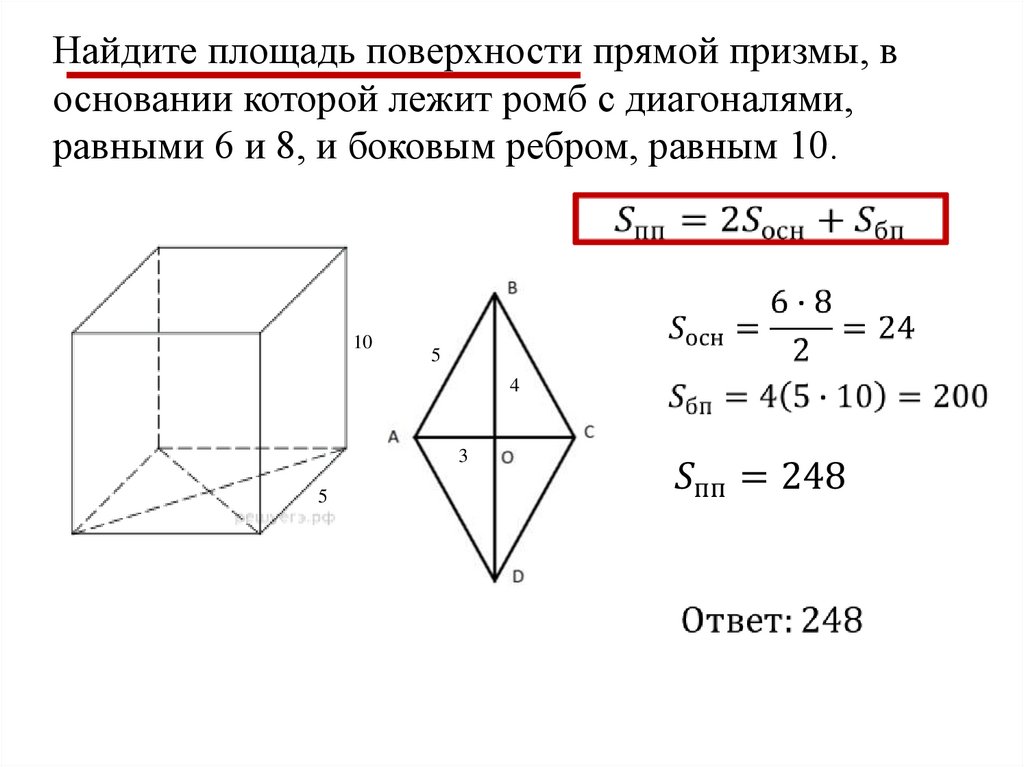
Найдите площадь поверхности прямой призмы, в
основании которой лежит ромб с диагоналями,
равными 6 и 8, и боковым ребром, равным 10.
10
5
4
3
5

20.

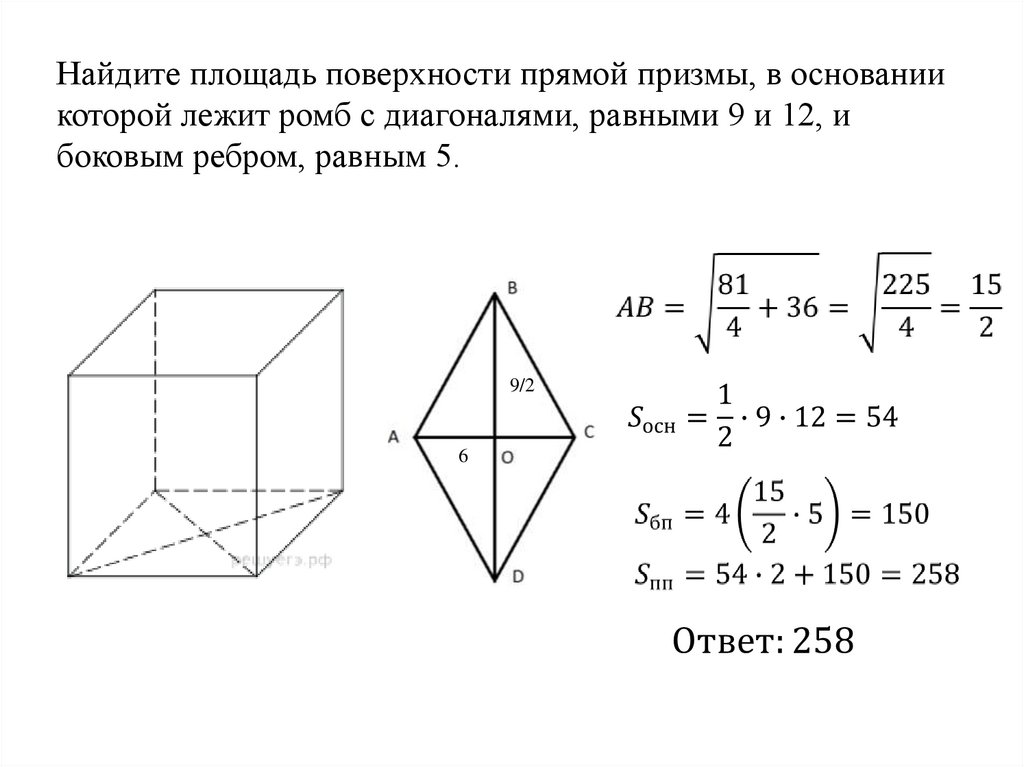
Найдите площадь поверхности прямой призмы, в основании
которой лежит ромб с диагоналями, равными 9 и 12, и
боковым ребром, равным 5.
9/2
6

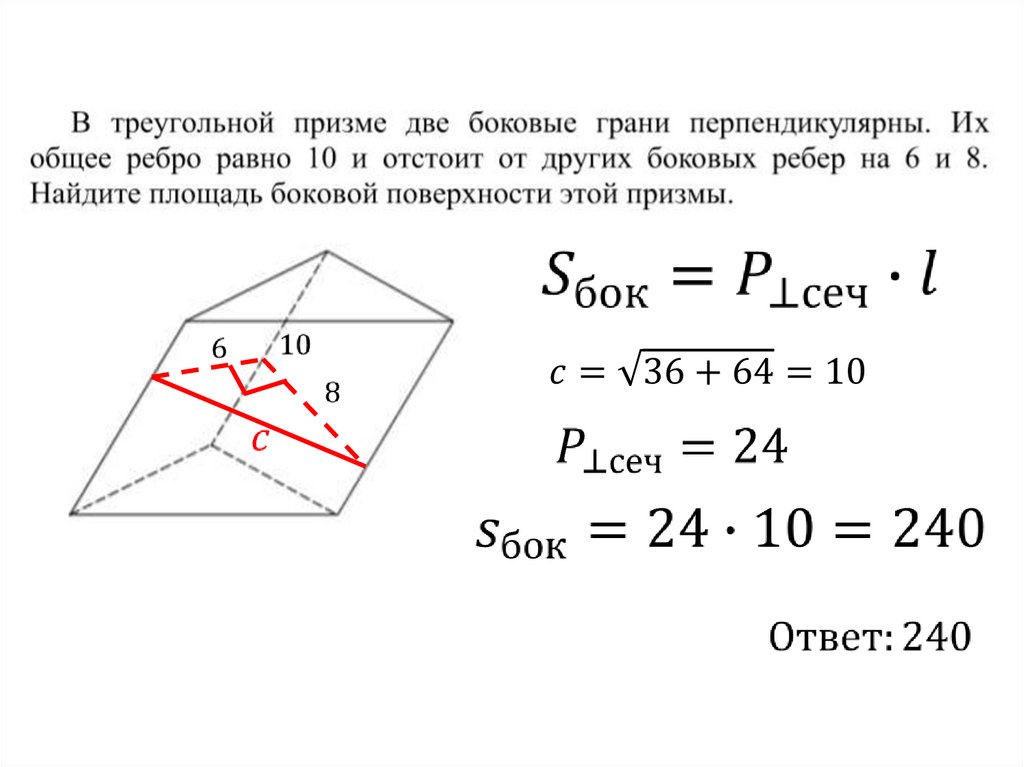
21.

Найдите площадь боковой поверхности прямой призмы, в
основании которой лежит прямоугольный треугольник с
катетами, равными 5 и 12, и боковым ребром, равным 8.

22.

23.

24.

25.

26.

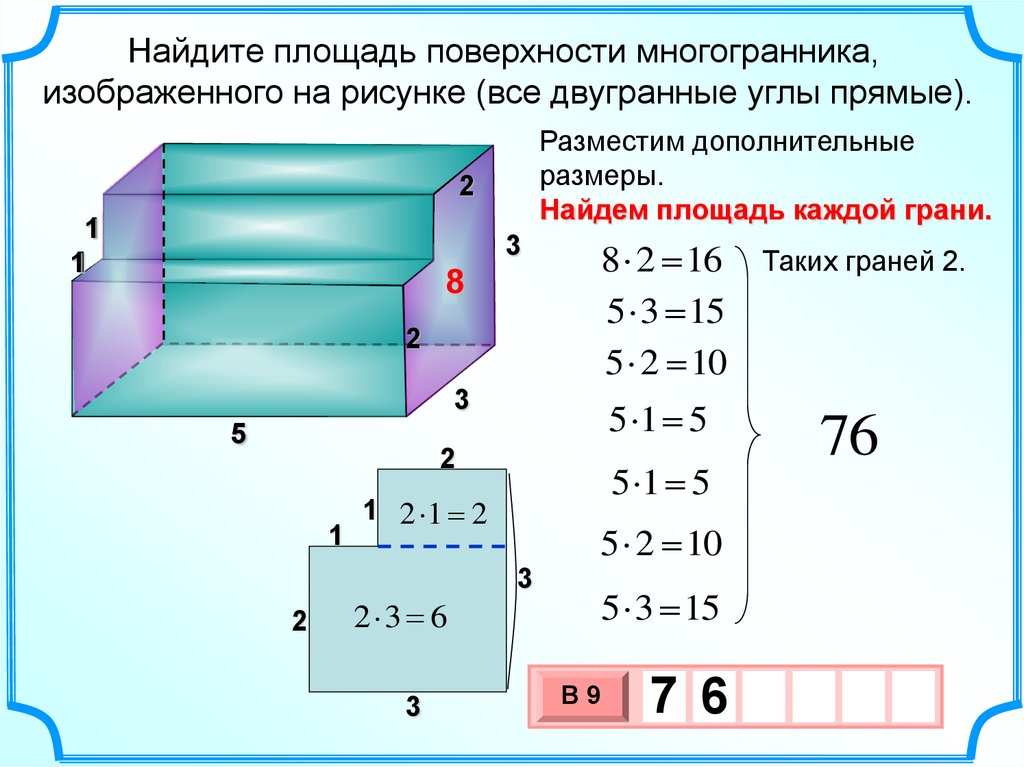
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
Разместим дополнительные
размеры.
Найдем площадь каждой грани.
2
1
1
3
8 2 16
5 3 15
5 2 10
8
2
3
5
5 1 5
2
1
1 2 1 2
5 2 10
5 3 15
2 3 6
3
76
5 1 5
3
2
Таких граней 2.
В9
7 6
3
10 х
х

27.

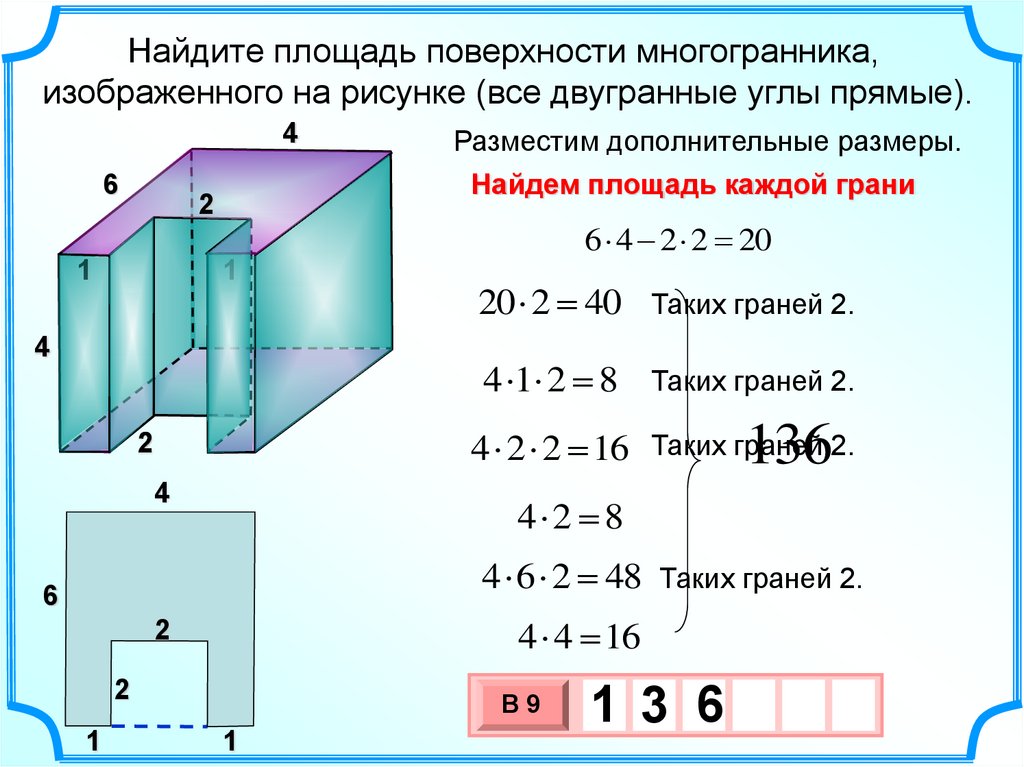
Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4
6
2
1
Разместим дополнительные размеры.
Найдем площадь каждой грани
6 4 2 2 20
1
4
2
4
20 2 40
Таких граней 2.
4 1 2 8
Таких граней 2.
4 2 2 16
Таких граней 2.
4 2 8
4 6 2 48
6
Таких граней 2.
4 4 16
2
2
1
136
В9
1
1 3 6
3
10 х
х

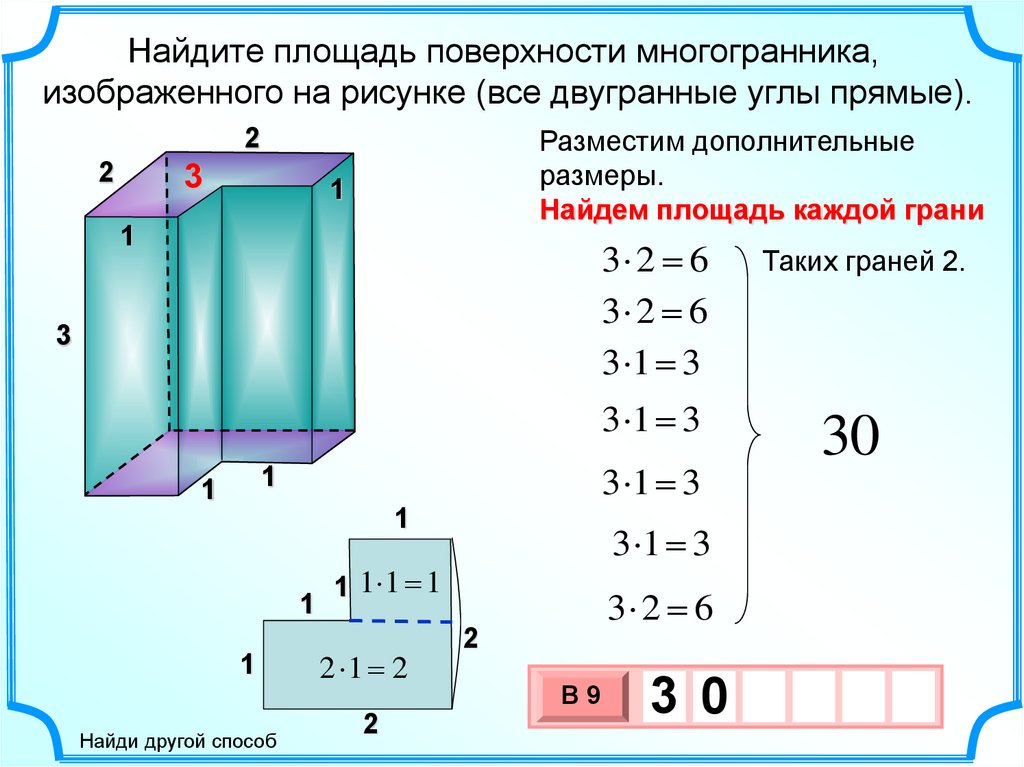
28.

Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
Разместим дополнительные
размеры.
Найдем площадь каждой грани
2
2
3
1
1
3 2 6
3 2 6
3 1 3
3
Таких граней 2.
3 1 3
3 1 3
1
1
1
1
1
Найди другой способ
30
3 1 3
1 1 1 1
2 1 2
2
3 2 6
2
В9
3 0
3
10 х
х

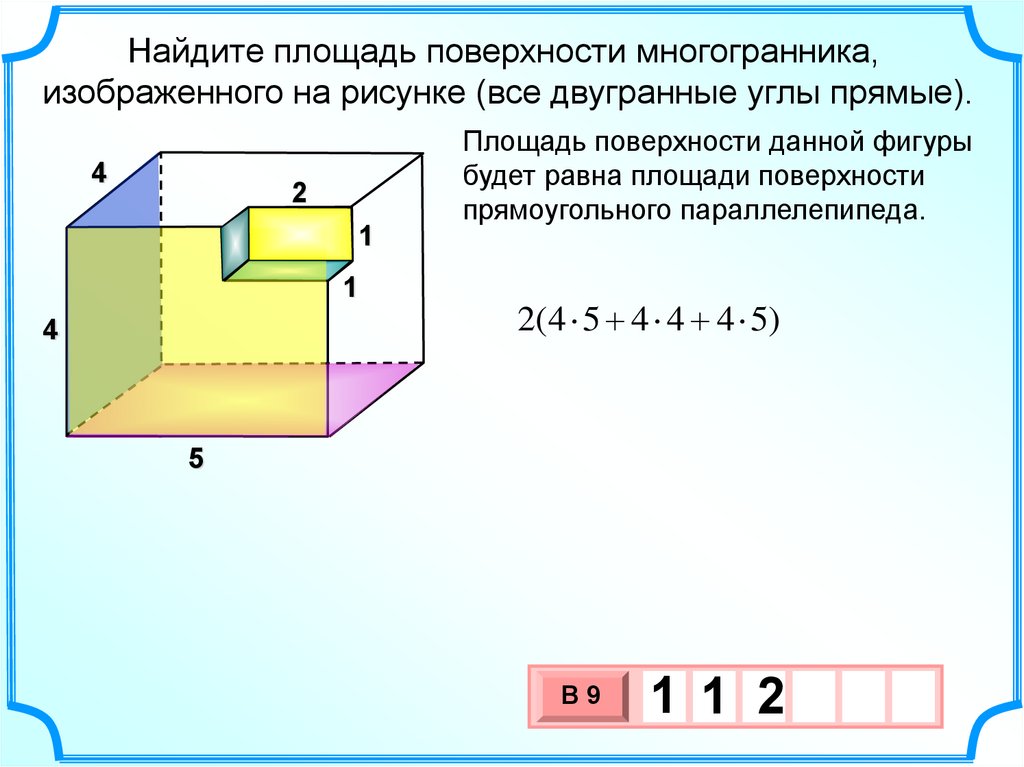
29.

Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
4
2
1
1
4
Площадь поверхности данной фигуры
будет равна площади поверхности
прямоугольного параллелепипеда.
2(4 5 4 4 4 5)
5
В9
1 1 2
3
10 х
х

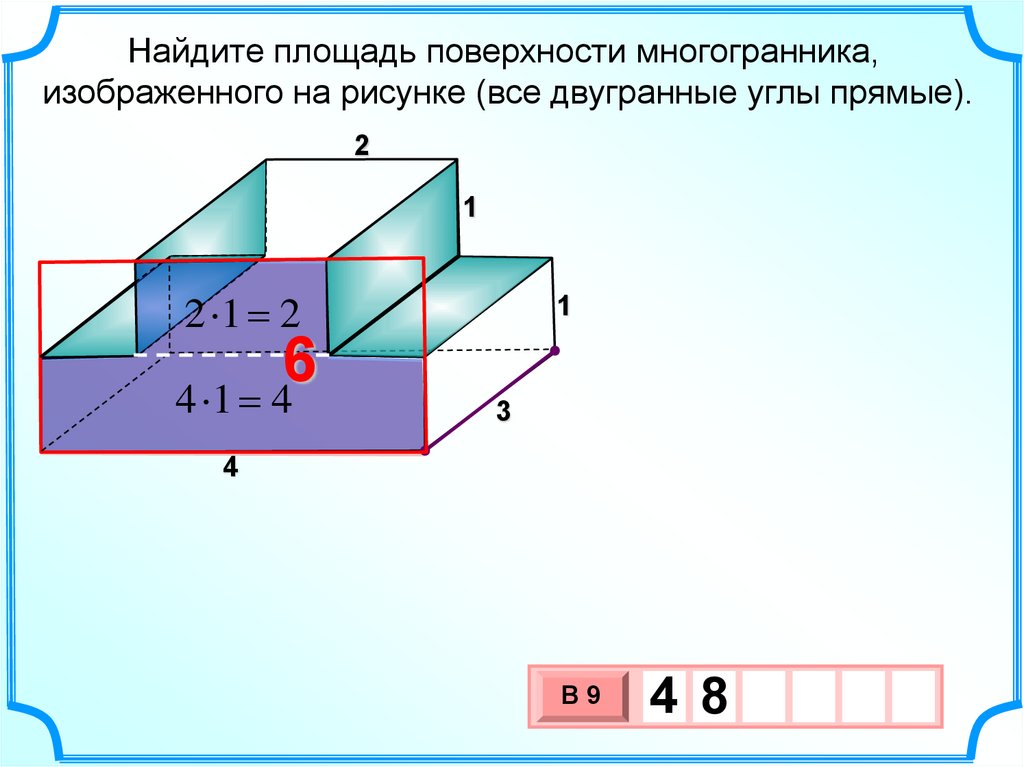
30.

Найдите площадь поверхности многогранника,
изображенного на рисунке (все двугранные углы прямые).
2
1
2 1 2
6
4 1 4
1
3
4
В9
4 8
3
10 х
х

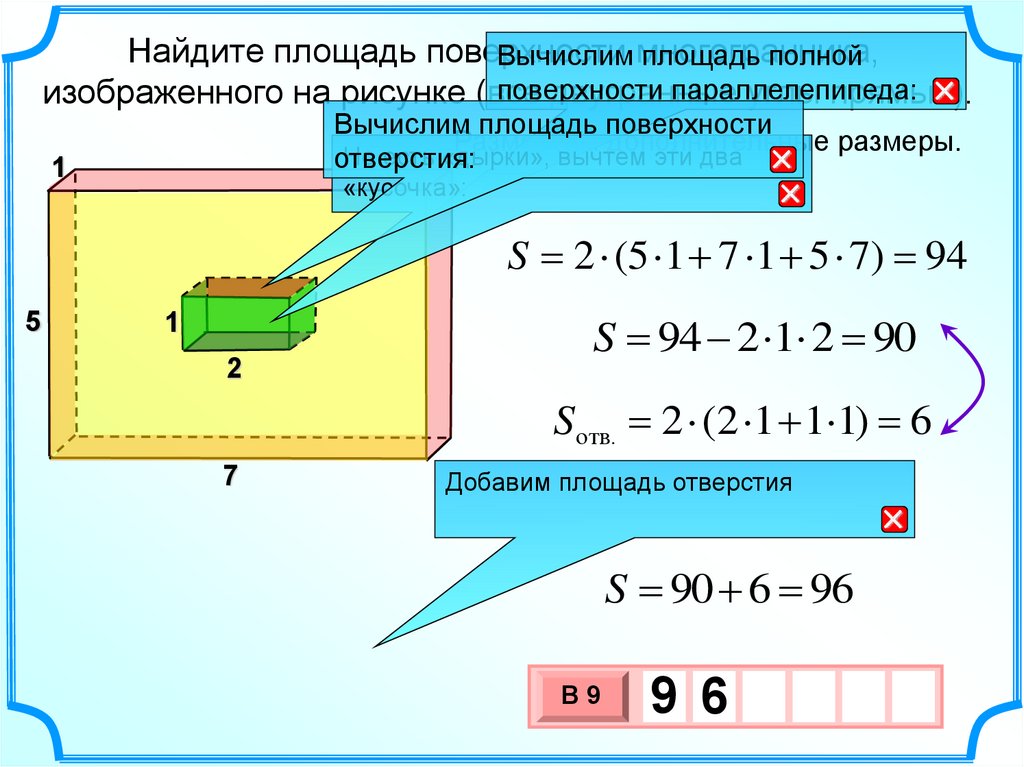
31.

Найдите площадь поверхности
Вычислим многогранника,
площадь полной
поверхности
параллелепипеда:
изображенного на рисунке (все
двугранные
углы прямые).
Вычислим площадь поверхности
Разместим дополнительные размеры.
Но есть «дырки», вычтем эти два
отверстия:
1
«кусочка»:
S 2 (5 1 7 1 5 7) 94
5
1
2
S 94 2 1 2 90
Sотв. 2 (2 1 1 1) 6
7
Добавим площадь отверстия
S 90 6 96
В9
9 6
3
10 х
х

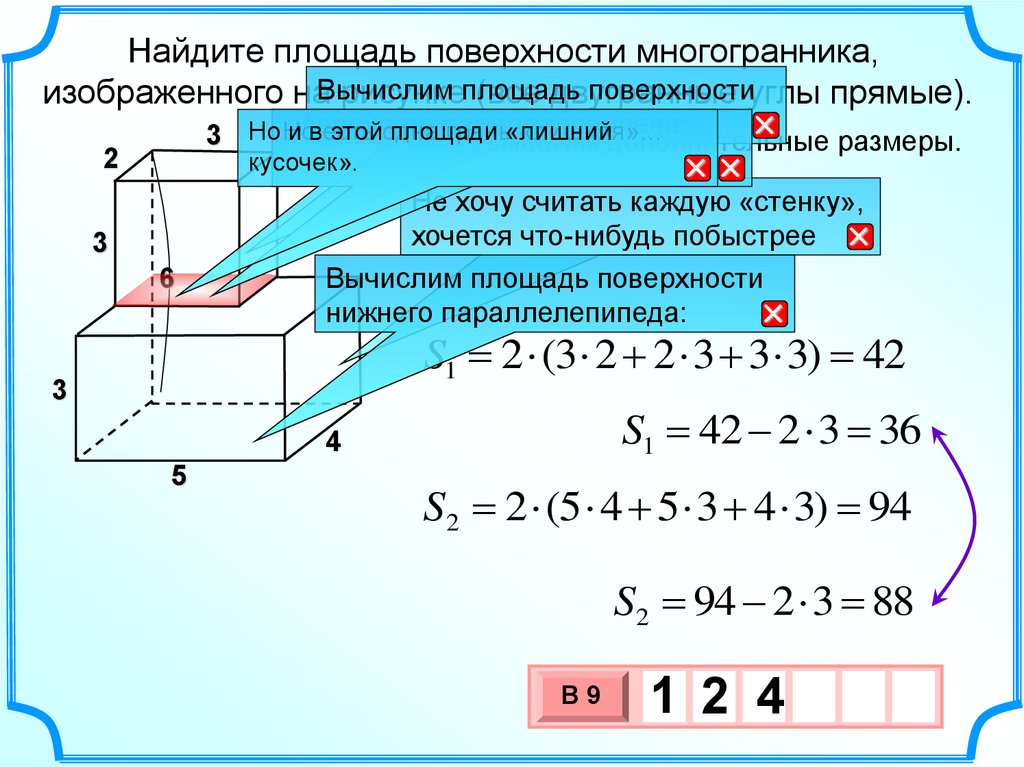
32.

Найдите площадь поверхности многогранника,
поверхностиуглы прямые).
изображенного наВычислим
рисункеплощадь
(все двугранные
параллелепипеда:
и вверхнего
есть
этойодна
площади
грань
«лишний
«лишняя»…
3 Но Но
Разместим
дополнительные размеры.
кусочек».
2
3
6
Не хочу считать каждую «стенку»,
хочется что-нибудь побыстрее
Вычислим площадь поверхности
нижнего параллелепипеда:
S1 2 (3 2 2 3 3 3) 42
3
S1 42 2 3 36
4
5
S2 2 (5 4 5 3 4 3) 94
S2 94 2 3 88
В9
1 2 4
3
10 х
х

33.

34.

35.

36.  

37.

38. Домашнее задание

• 1) Выучить теорию по теме «Многогранники.
Призма»: п.27, 30
• 2) Решить ПРОТОТИПЫ ЕГЭ