Similar presentations:
Понятие многогранника. Призма
1.
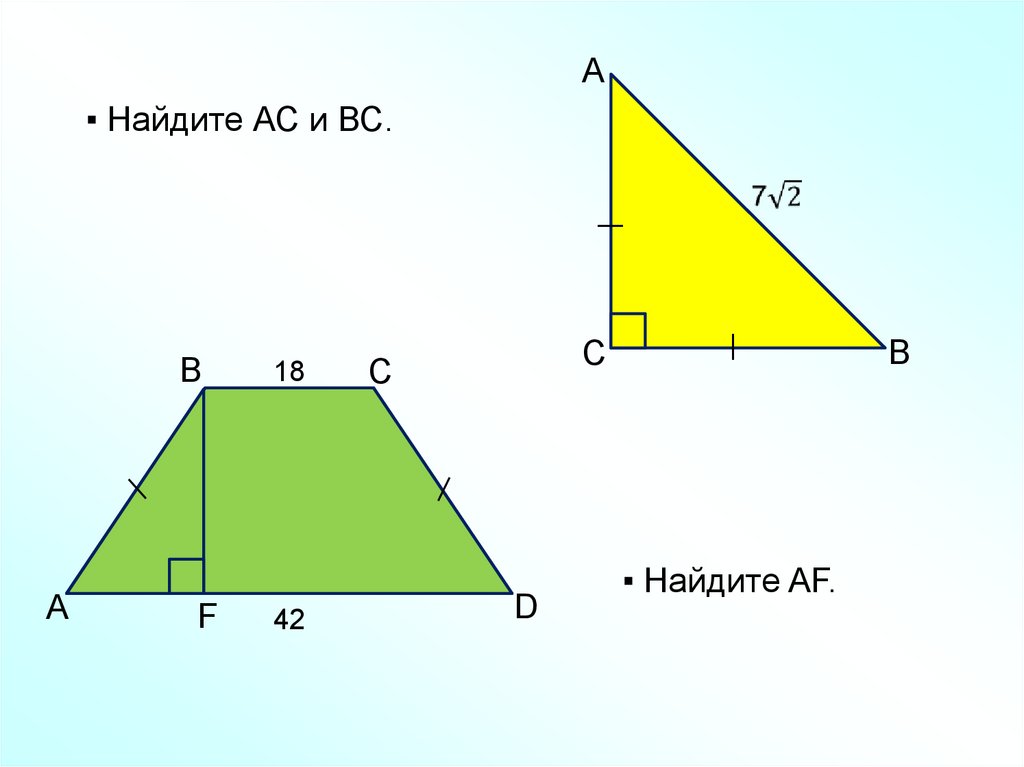
А▪ Найдите АС и ВС.
—
А
F
18
42
С
С
D
—
B
▪ Найдите AF.
В
2.
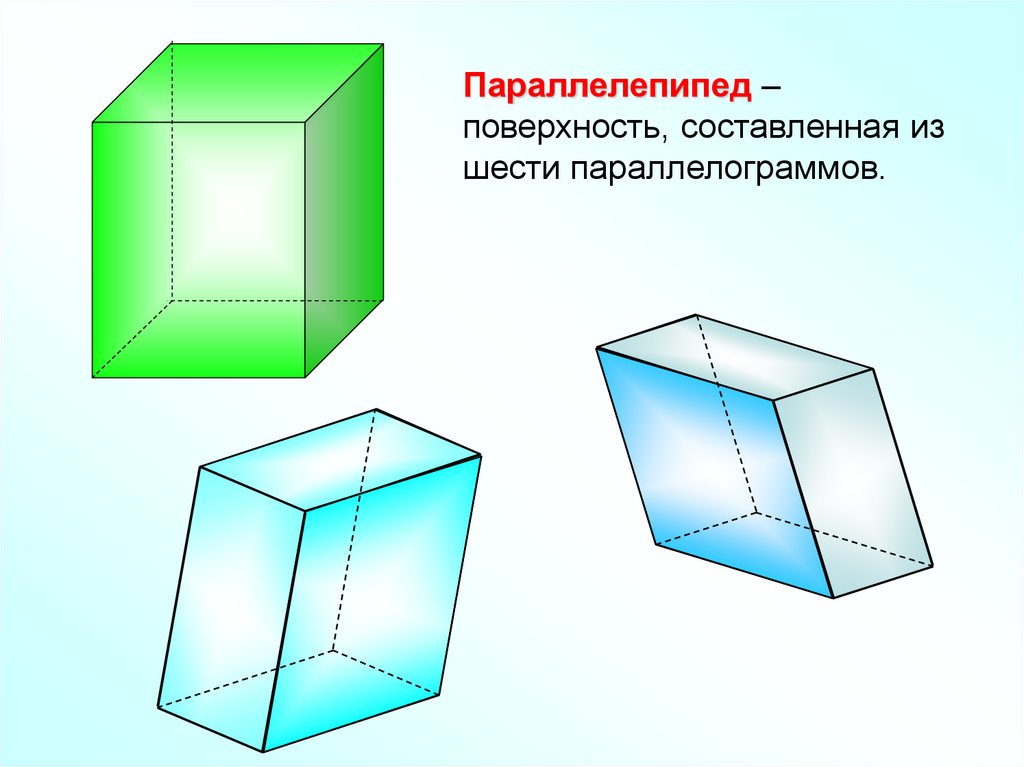
Параллелепипед –поверхность, составленная из
шести параллелограммов.
3.
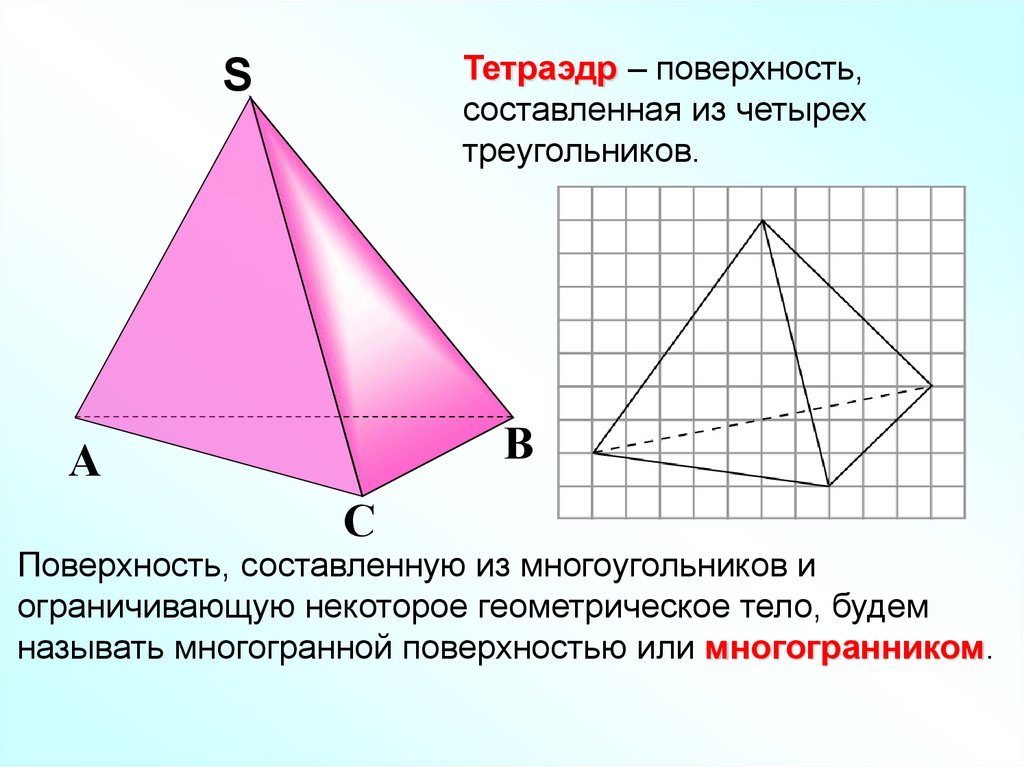
Тетраэдр – поверхность,составленная из четырех
треугольников.
SS
В
А
С
Поверхность, составленную из многоугольников и
ограничивающую некоторое геометрическое тело, будем
называть многогранной поверхностью или многогранником.
4.
5.
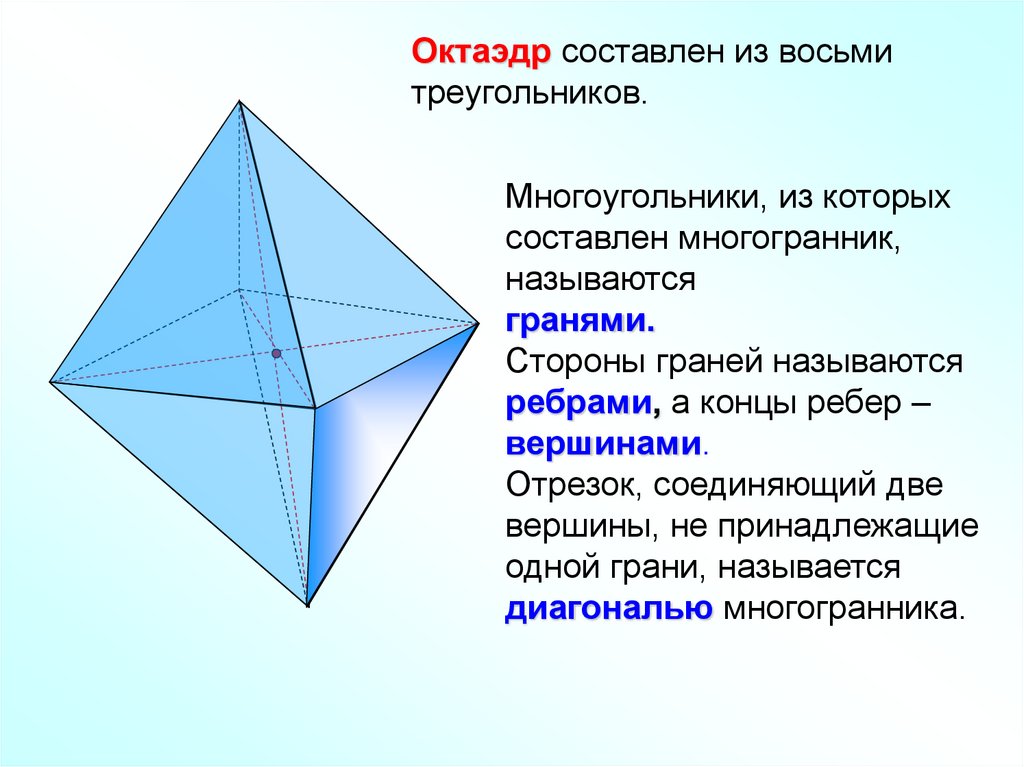
Октаэдр составлен из восьмитреугольников.
Многоугольники, из которых
составлен многогранник,
называются
гранями.
Стороны граней называются
ребрами, а концы ребер –
вершинами.
Отрезок, соединяющий две
вершины, не принадлежащие
одной грани, называется
диагональю многогранника.
6.
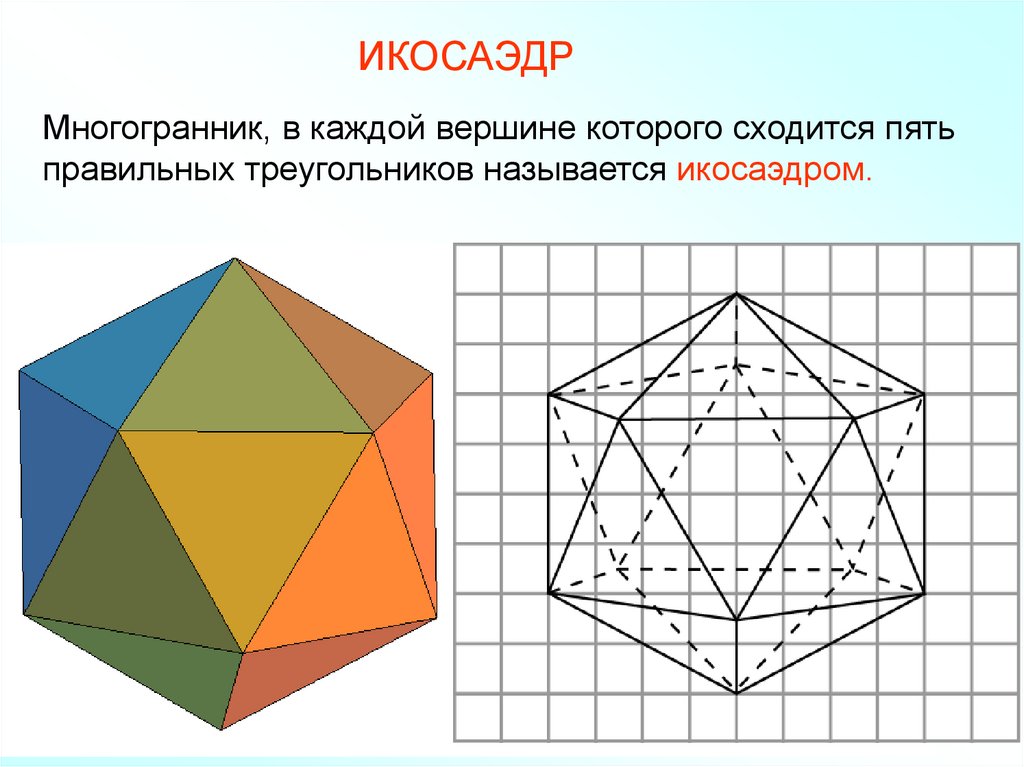
ИКОСАЭДРМногогранник, в каждой вершине которого сходится пять
правильных треугольников называется икосаэдром.
7.
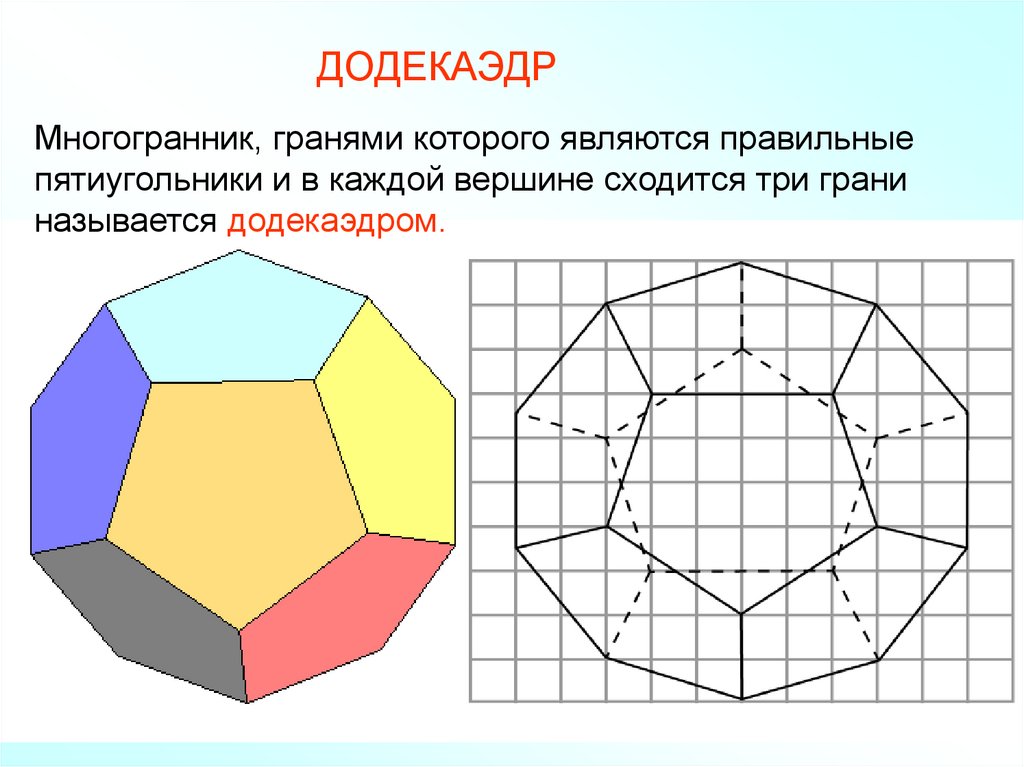
ДОДЕКАЭДРМногогранник, гранями которого являются правильные
пятиугольники и в каждой вершине сходится три грани
называется додекаэдром.
8.
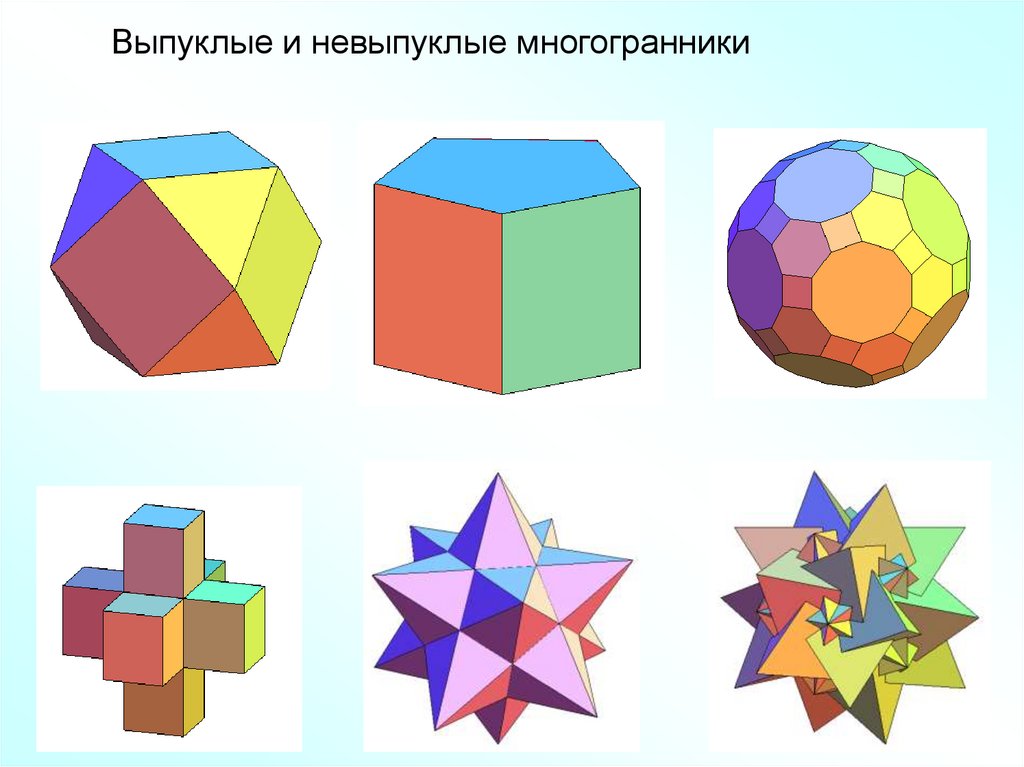
Выпуклые и невыпуклые многогранники9.
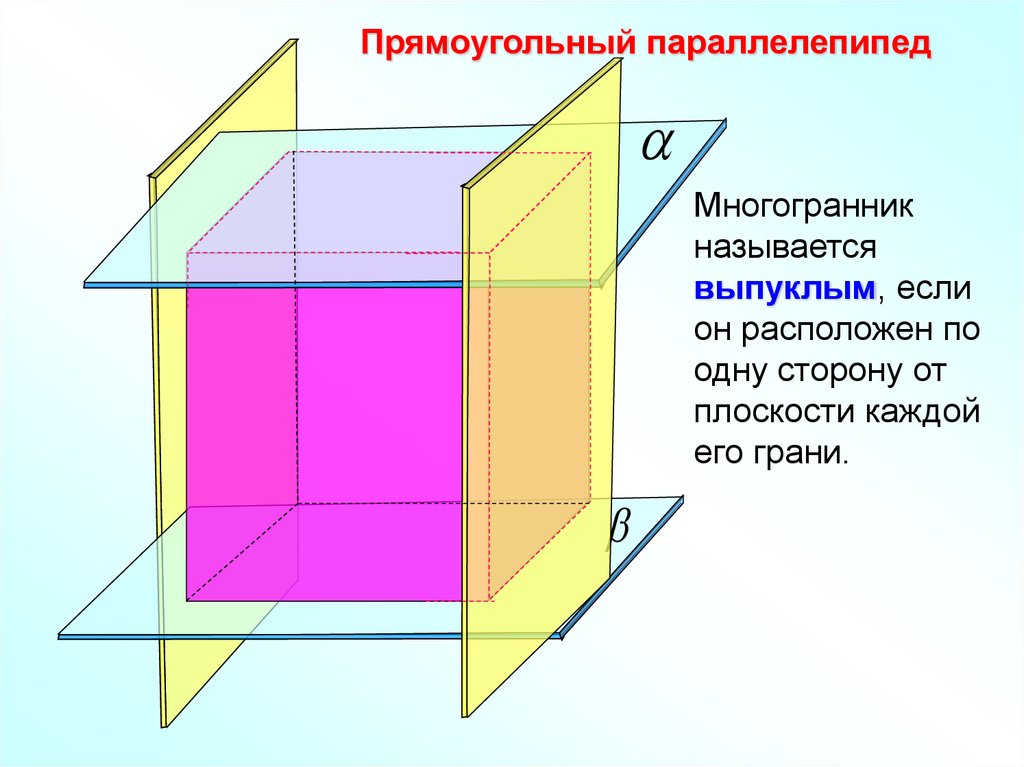
Прямоугольный параллелепипедМногогранник
называется
выпуклым, если
он расположен по
одну сторону от
плоскости каждой
его грани.
10.
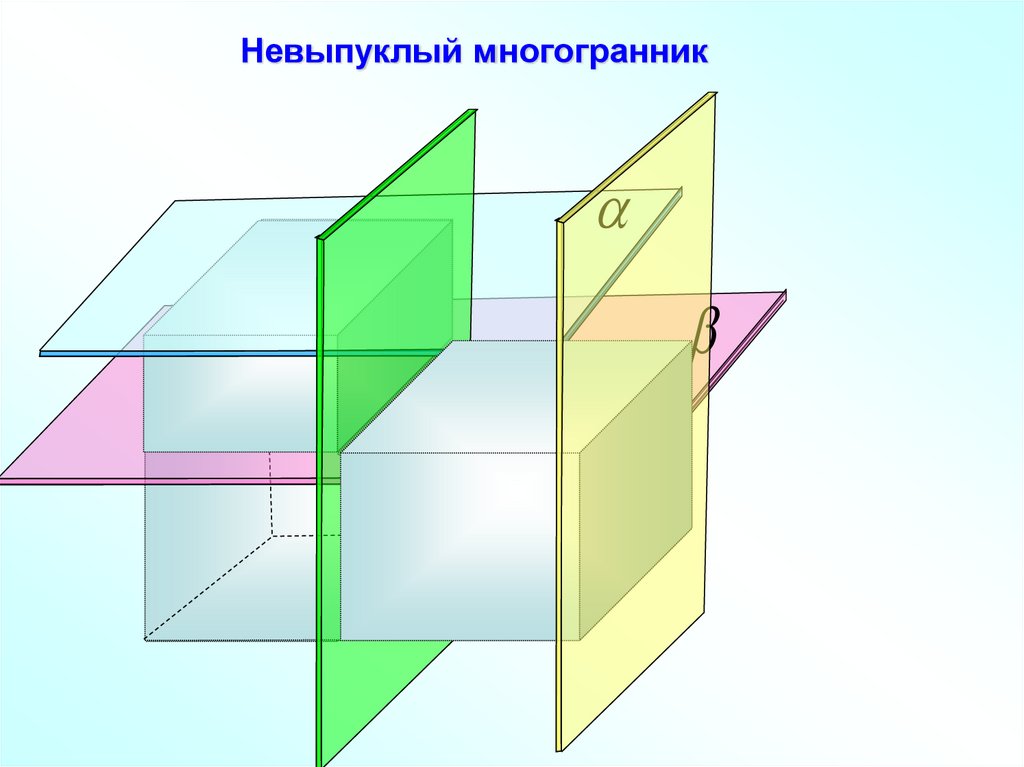
Невыпуклый многогранник11.
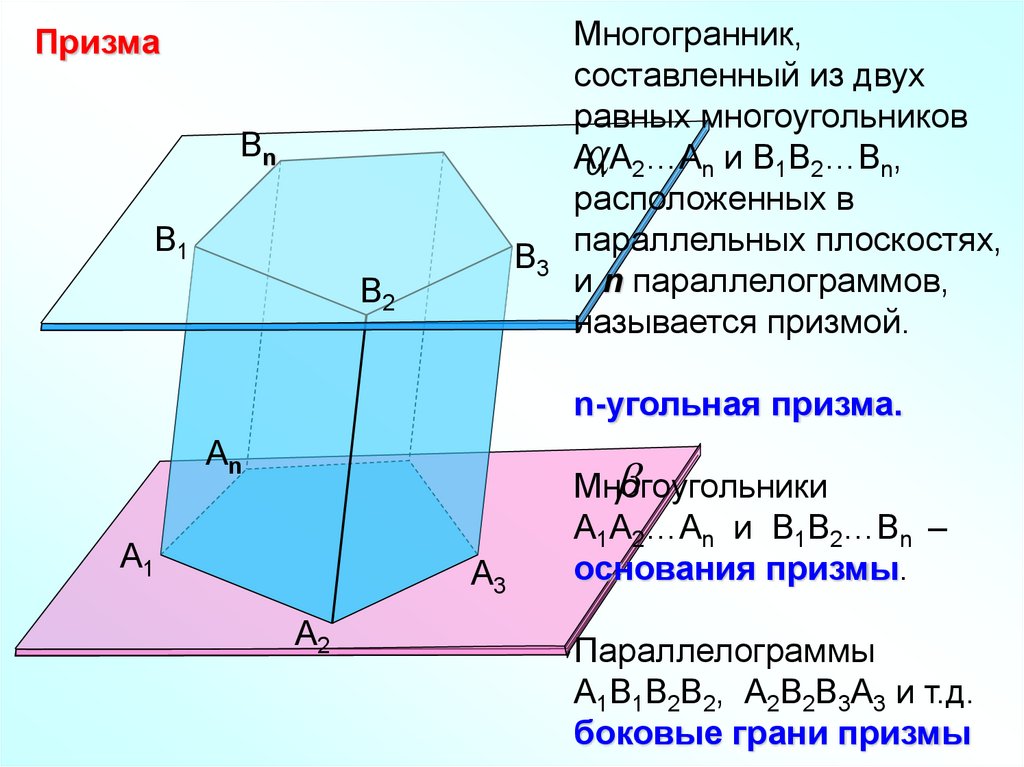
ПризмаМногогранник,
составленный из двух
равных многоугольников
А1А2…Аn и В1В2…Вn,
расположенных в
параллельных плоскостях,
и n параллелограммов,
называется призмой.
Bn
B1
B3
B2
n-угольная призма.
Аn
А1
А3
А2
Многоугольники
А1А2…Аn и В1В2…Вn –
основания призмы.
Параллелограммы
А1В1В2В2, А2В2В3А3 и т.д.
боковые грани призмы
12.
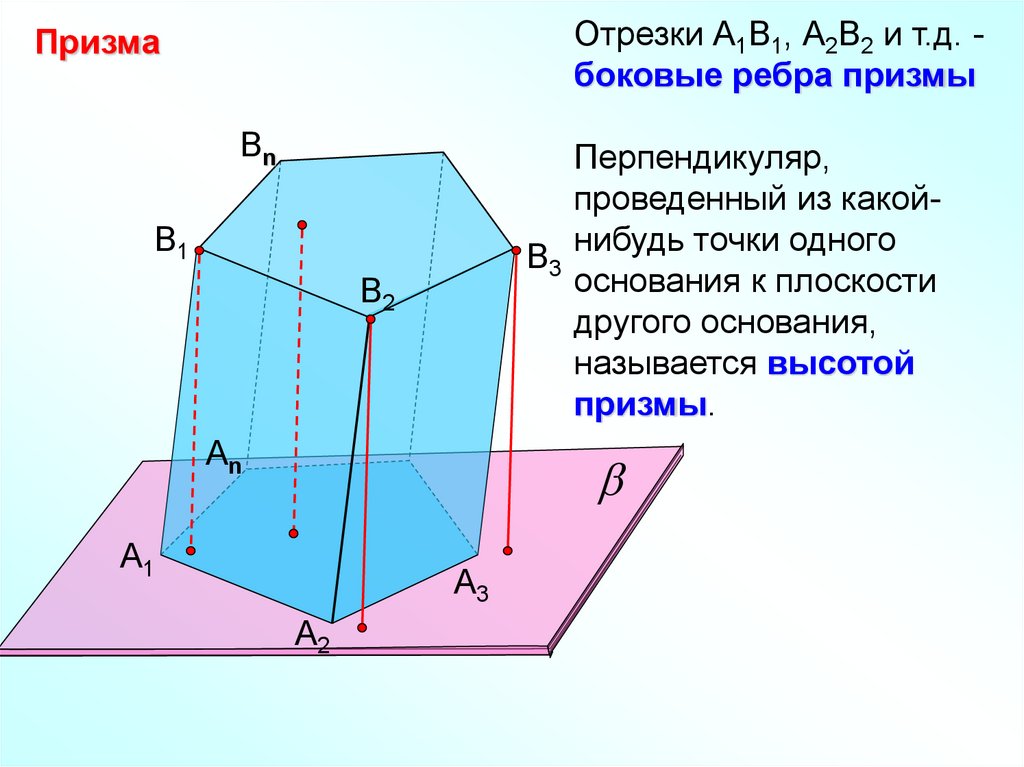
Отрезки А1В1, А2В2 и т.д. боковые ребра призмыПризма
Bn
Перпендикуляр,
проведенный из какойB3 нибудь точки одного
основания к плоскости
другого основания,
называется высотой
призмы.
B1
B2
Аn
А1
А3
А2
13.
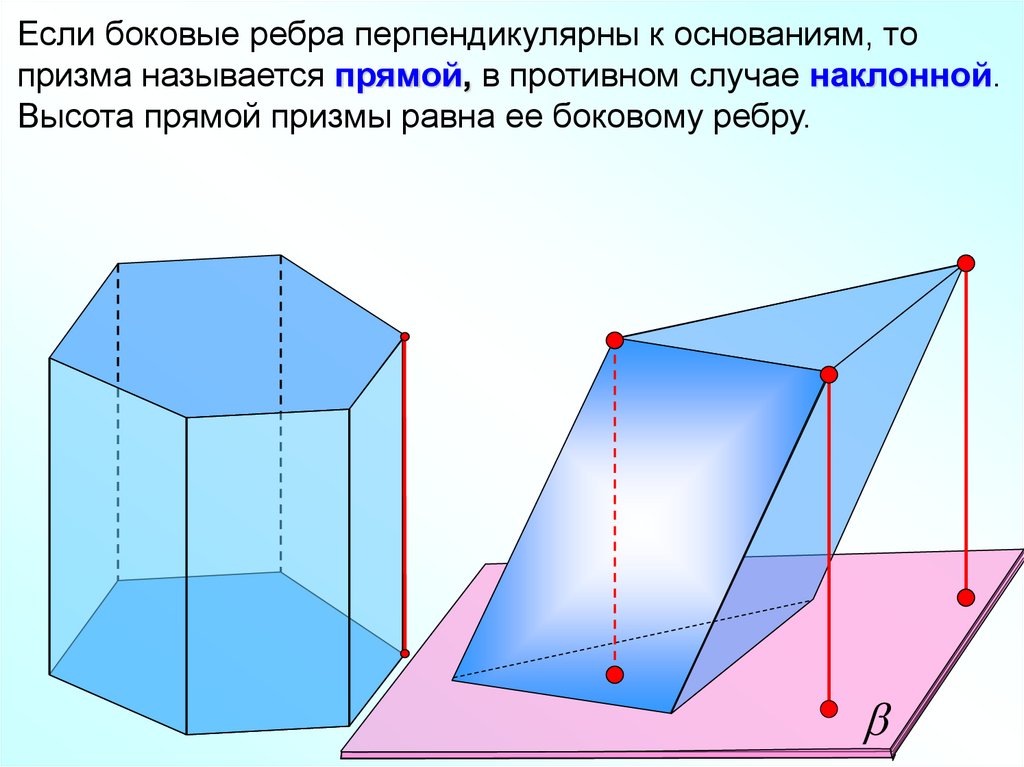
Если боковые ребра перпендикулярны к основаниям, топризма называется прямой, в противном случае наклонной.
Высота прямой призмы равна ее боковому ребру.
14.
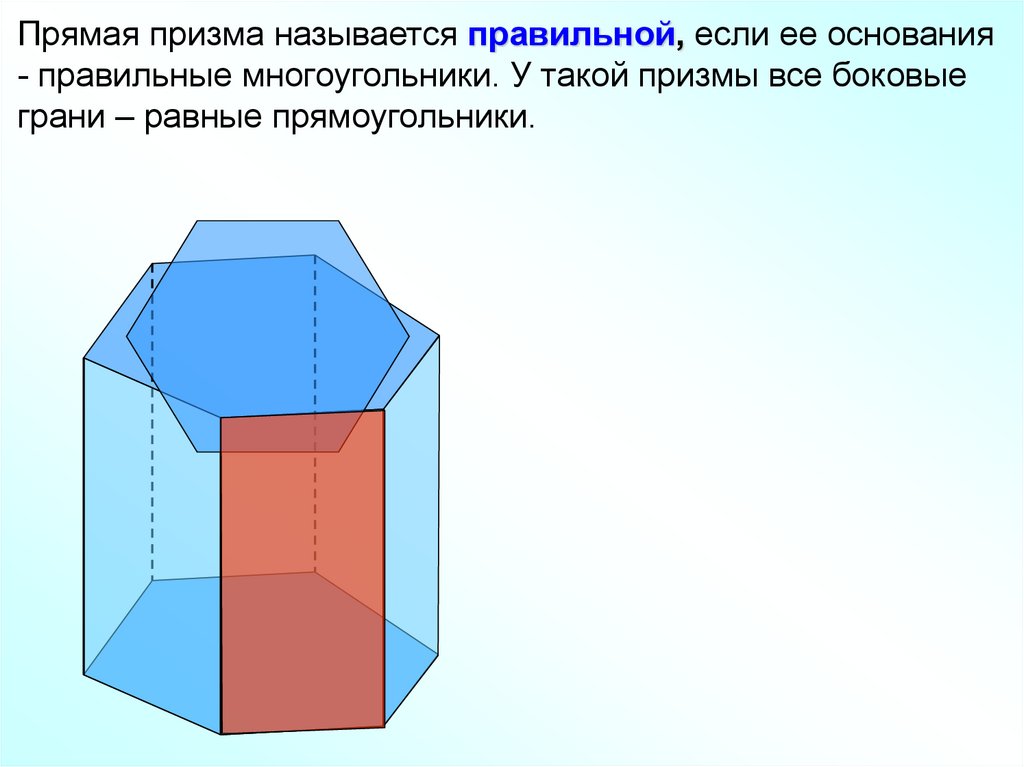
Прямая призма называется правильной, если ее основания- правильные многоугольники. У такой призмы все боковые
грани – равные прямоугольники.
15.
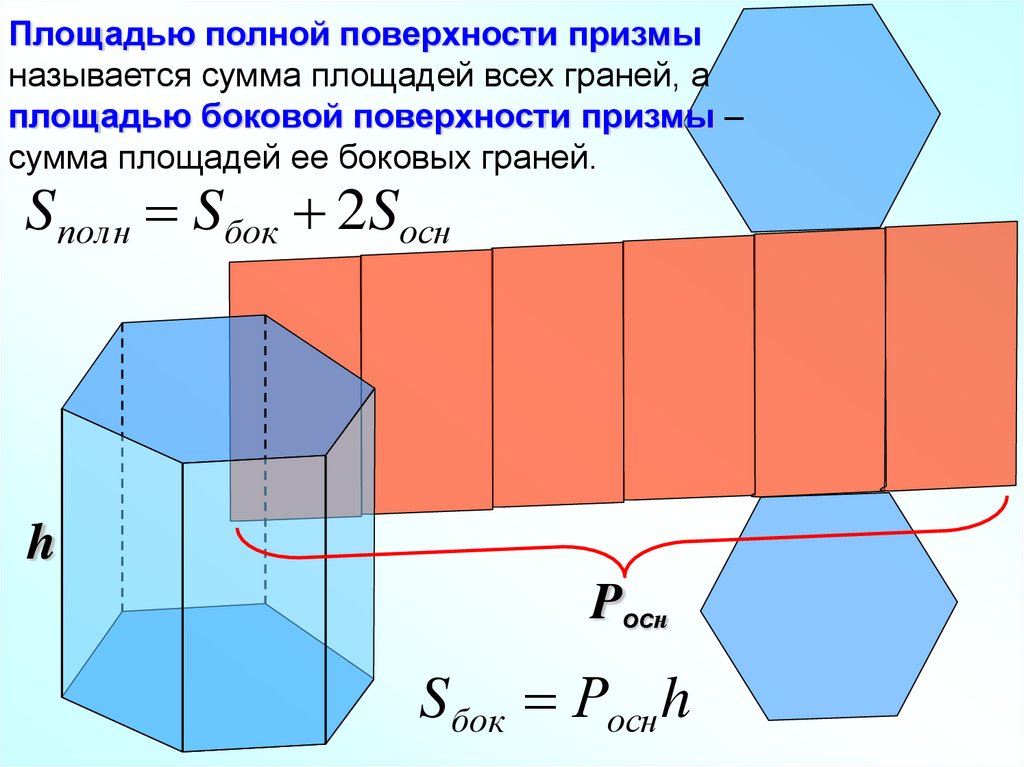
Площадью полной поверхности призмыназывается сумма площадей всех граней, а
площадью боковой поверхности призмы –
сумма площадей ее боковых граней.
S полн Sбок 2Sосн
h
Pocн
Sбок Росн h
16.
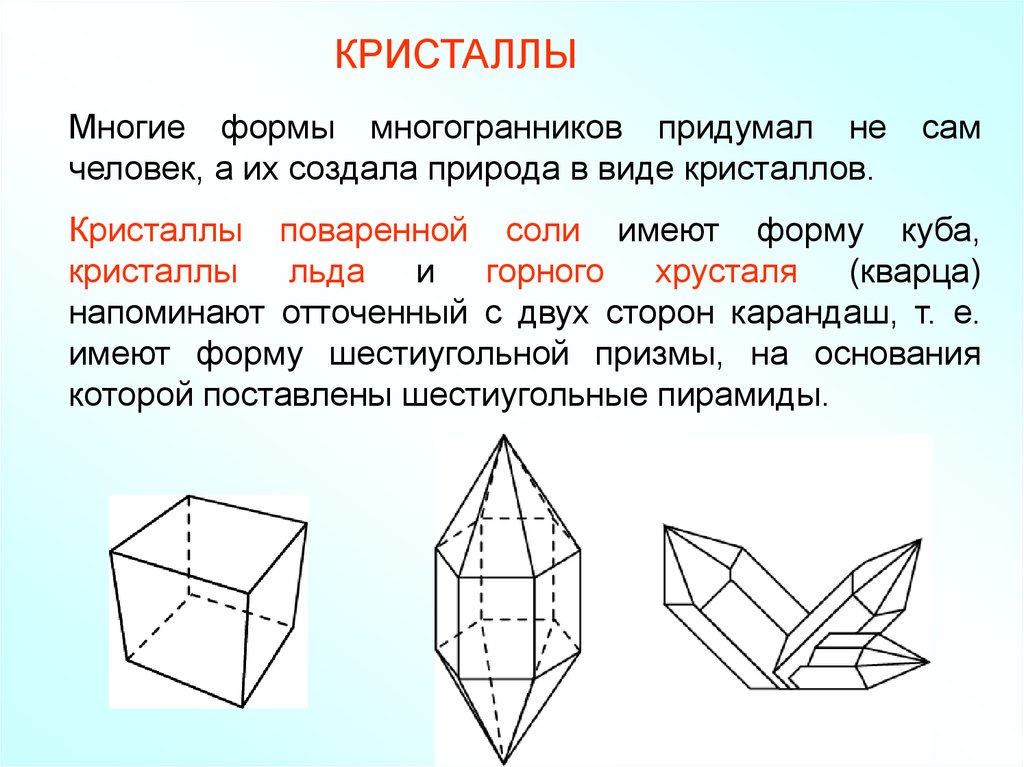
КРИСТАЛЛЫМногие формы многогранников придумал не
человек, а их создала природа в виде кристаллов.
сам
Кристаллы поваренной соли имеют форму куба,
кристаллы льда и горного хрусталя (кварца)
напоминают отточенный с двух сторон карандаш, т. е.
имеют форму шестиугольной призмы, на основания
которой поставлены шестиугольные пирамиды.
17.
Кристаллы – природныемногогранники
Здесь представлены
фотографии кристаллов
минералогического музея
им. А.Е. Ферсмана в
Москве, информацию о
котором можно узнать на
сайте www.fmm.ru
18.
Алмаз19.
Аметист20.
Изумруд21.
Кварц22.
Сера23.
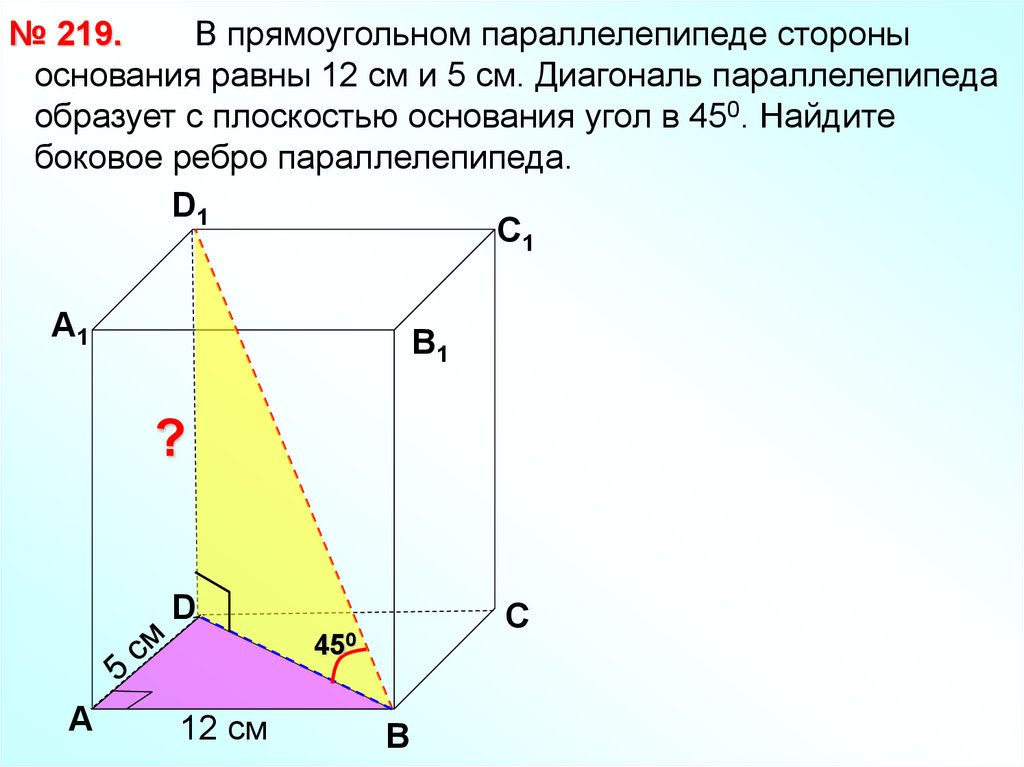
№ 219.В прямоугольном параллелепипеде стороны
основания равны 12 см и 5 см. Диагональ параллелепипеда
образует с плоскостью основания угол в 450. Найдите
боковое ребро параллелепипеда.
D1
С1
А1
В1
?
D
С
450
А
12 см
В
24.
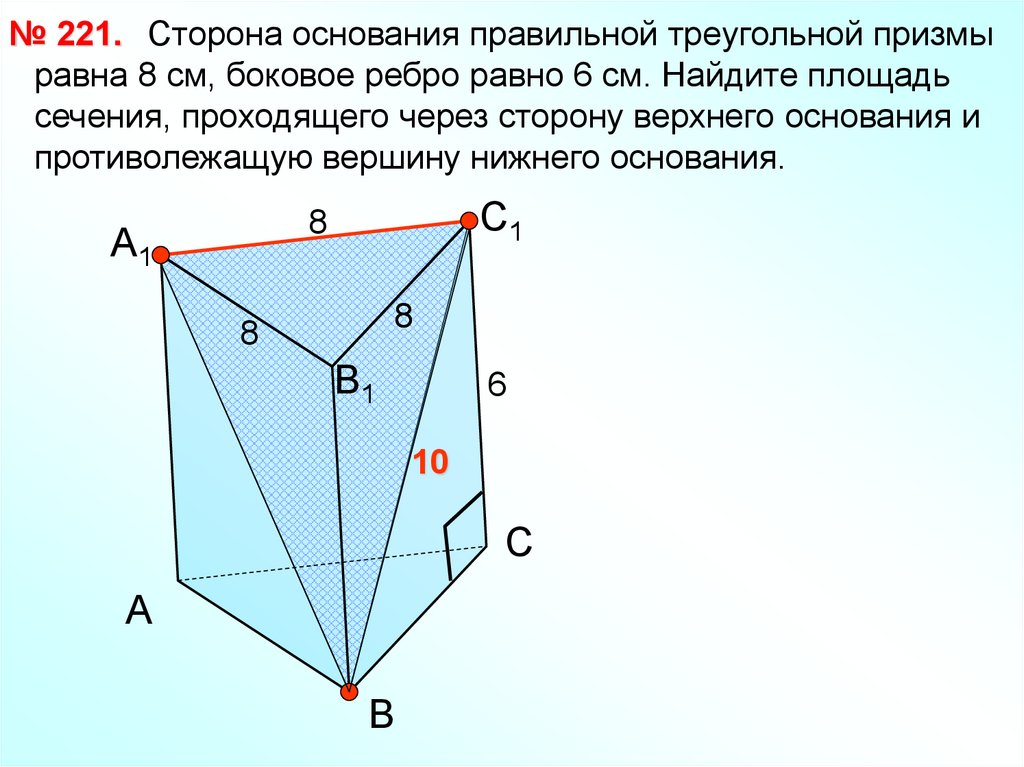
№ 221. Сторона основания правильной треугольной призмыравна 8 см, боковое ребро равно 6 см. Найдите площадь
сечения, проходящего через сторону верхнего основания и
противолежащую вершину нижнего основания.
С1
8
А1
8
8
В1
6
10
С
А
В
25.
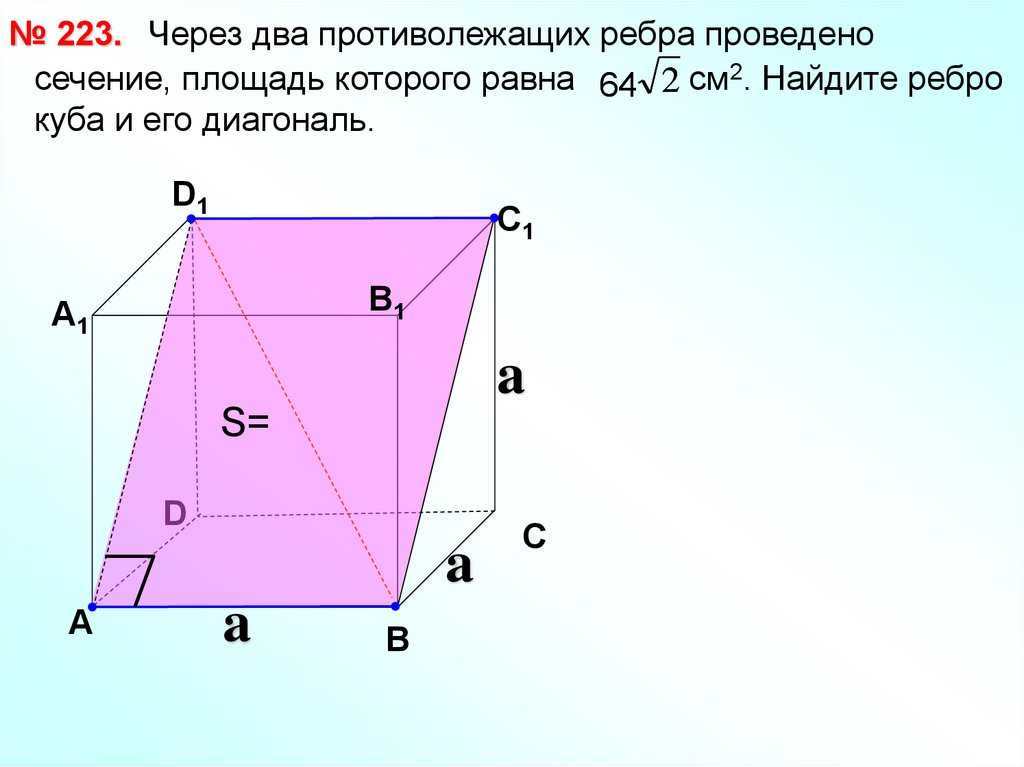
№ 223. Через два противолежащих ребра проведеносечение, площадь которого равна 64 2 см2. Найдите ребро
куба и его диагональ.
D1
С1
В1
А1
a
S=
D
a
А
a
В
С
26.
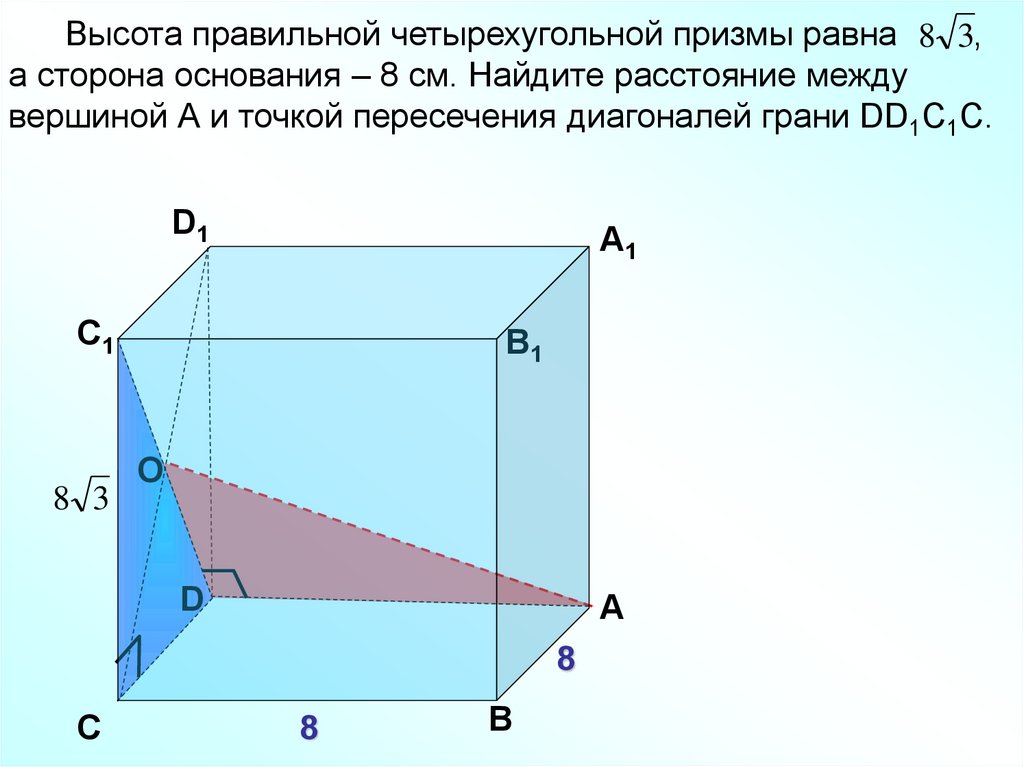
Высота правильной четырехугольной призмы равна 8 3,а сторона основания – 8 см. Найдите расстояние между
вершиной А и точкой пересечения диагоналей грани DD1С1С.
D1
А1
С1
8 3
В1
О
D
А
8
С
8
В
27.
Домашнее задание: конспект.Выполнить задачи с слайда
28.
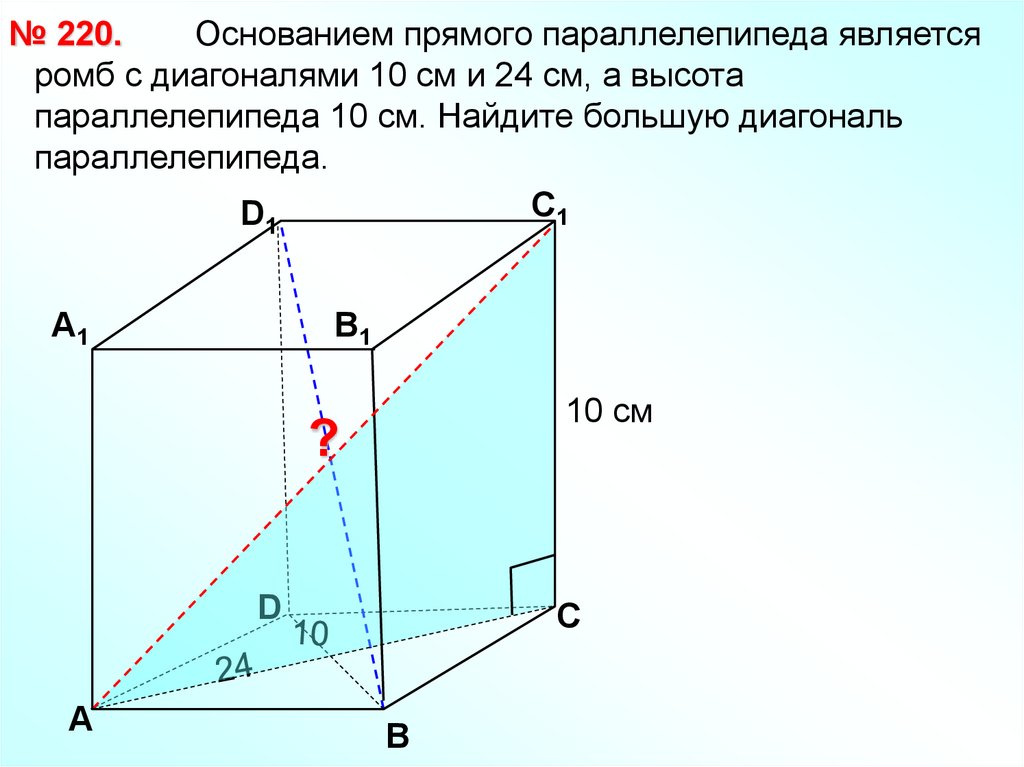
№ 220.Основанием прямого параллелепипеда является
ромб с диагоналями 10 см и 24 см, а высота
параллелепипеда 10 см. Найдите большую диагональ
параллелепипеда.
С1
D1
А1
В1
10 см
?
D
А
С
В
29.
Сторона основания правильной треугольной призмыравна 8 см, а диагональ боковой грани равна 10 см.
Найдите площадь боковой и полной поверхности
призмы.
30.
№ 222. Основанием прямой призмы являетсяравнобедренная трапеция с основаниями 25 см и 9 см и
высотой 8 см. Найдите двугранные углы при боковых ребрах
призмы.
D1
С1
А1
В1
D
9
С
25
F 8
8
А
8 H
В










 mathematics
mathematics








