Призма

1.

Призма
Преподаватель математики
Костенкова С.С.
2018г

2.

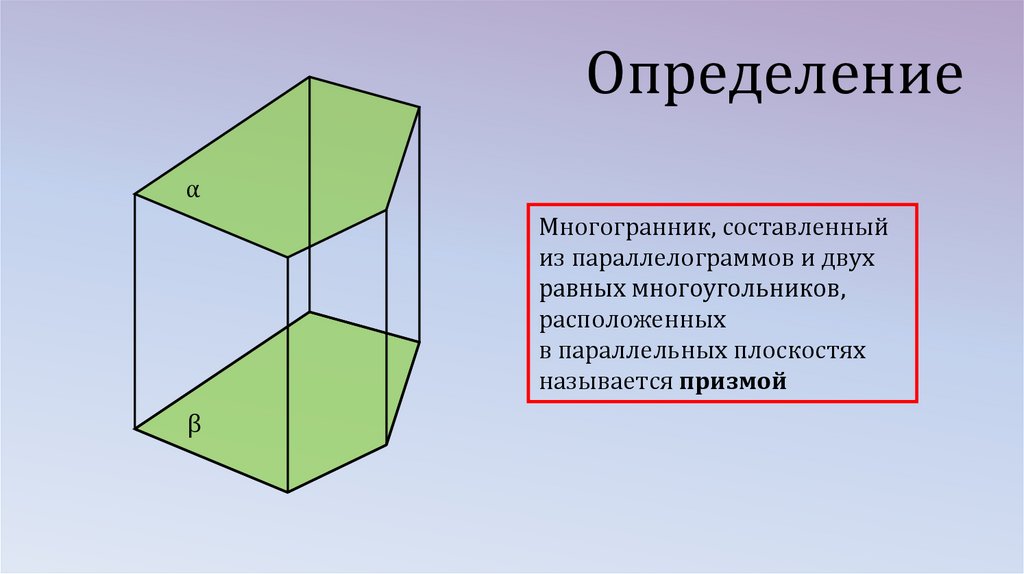
Определение
α
Многогранник, составленный
из параллелограммов и двух
равных многоугольников,
расположенных
в параллельных плоскостях
называется призмой
β

3.

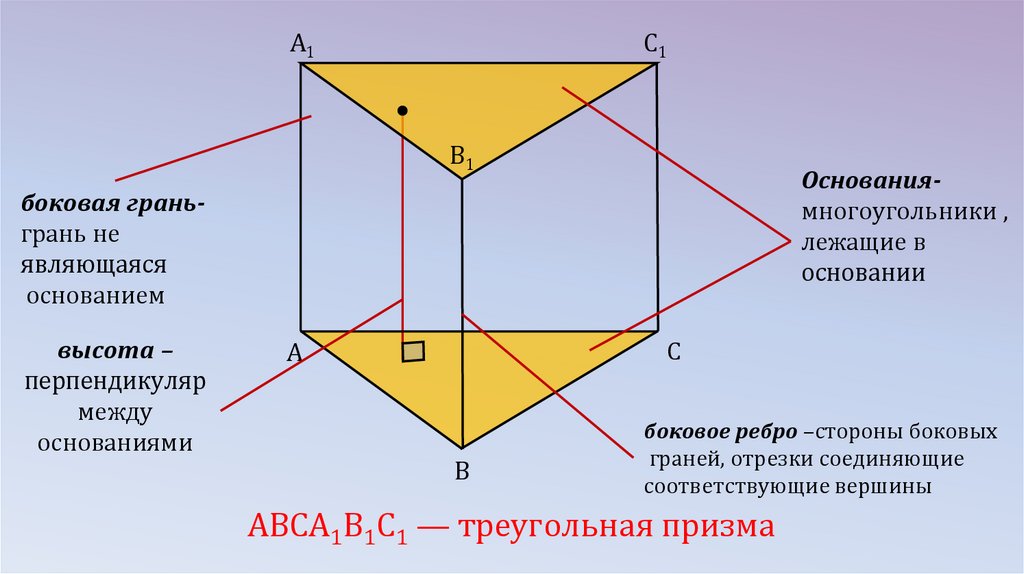
Основные элементы

4.

A1
C1
B1
Основаниямногоугольники ,
лежащие в
основании
боковая граньгрань не
являющаяся
основанием
высота –
перпендикуляр
между
основаниями
C
A
B
боковое ребро –стороны боковых
граней, отрезки соединяющие
соответствующие вершины
АВСA1B1C1 — треугольная призма

5.

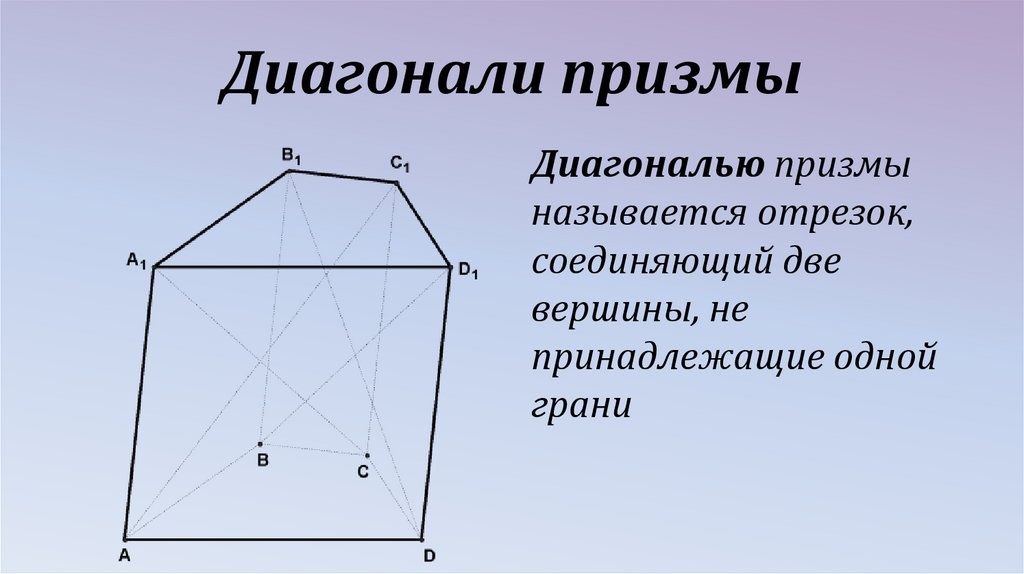
Диагонали призмы
Диагональю призмы
называется отрезок,
соединяющий две
вершины, не
принадлежащие одной
грани

6.

Свойства призмы
1.
Основания призмы равны.
2.
Основания призмы лежат в параллельных
плоскостях.
3.
Боковые ребра призмы параллельны и равны.
4.
Боковые грани наклонной призмы параллелограммы, прямой призмы - прямоугольники.

7.

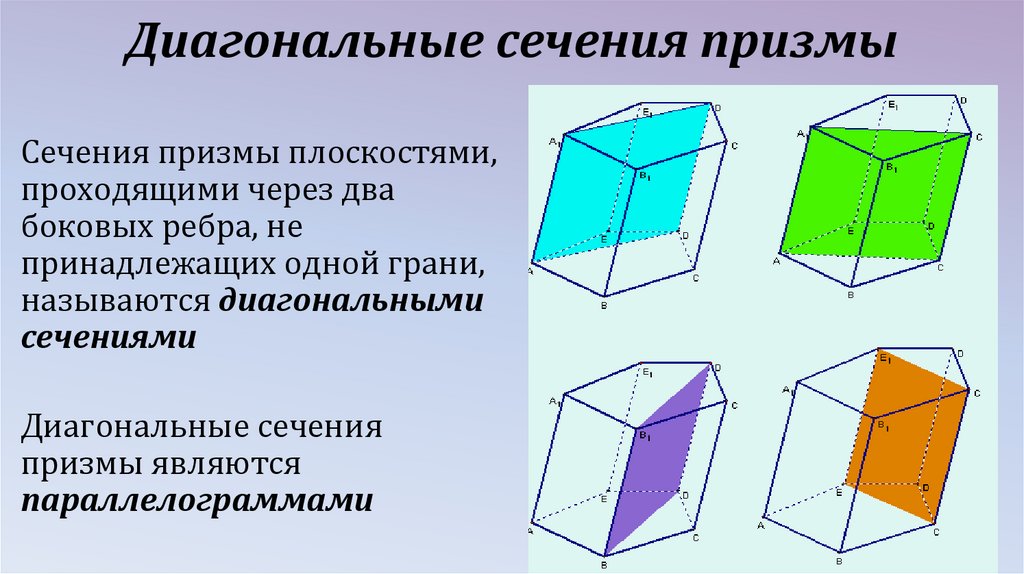
Диагональные сечения призмы
Сечения призмы плоскостями,
проходящими через два
боковых ребра, не
принадлежащих одной грани,
называются диагональными
сечениями
Диагональные сечения
призмы являются
параллелограммами

8.

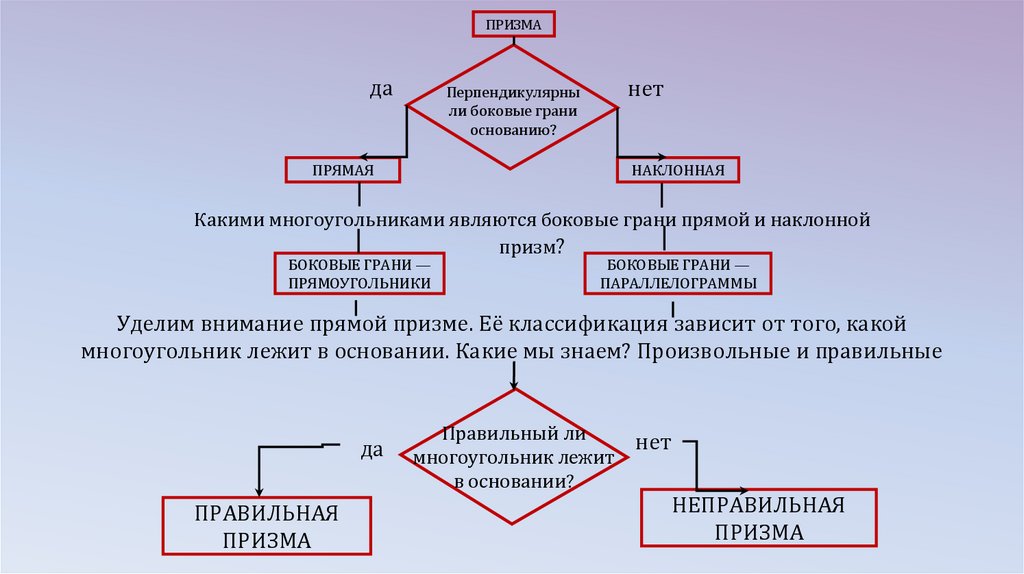
Классификация призм

9.

ПРИЗМА
да
нет
Перпендикулярны
ли боковые грани
основанию?
ПРЯМАЯ
НАКЛОННАЯ
Какими многоугольниками являются боковые грани прямой и наклонной
призм?
БОКОВЫЕ ГРАНИ —
ПРЯМОУГОЛЬНИКИ
БОКОВЫЕ ГРАНИ —
ПАРАЛЛЕЛОГРАММЫ
Уделим внимание прямой призме. Её классификация зависит от того, какой
многоугольник лежит в основании. Какие мы знаем? Произвольные и правильные
да
ПРАВИЛЬНАЯ
ПРИЗМА
Правильный ли
многоугольник лежит
в основании?
нет
НЕПРАВИЛЬНАЯ
ПРИЗМА

10.

Формулы поверхностей
призм

11.

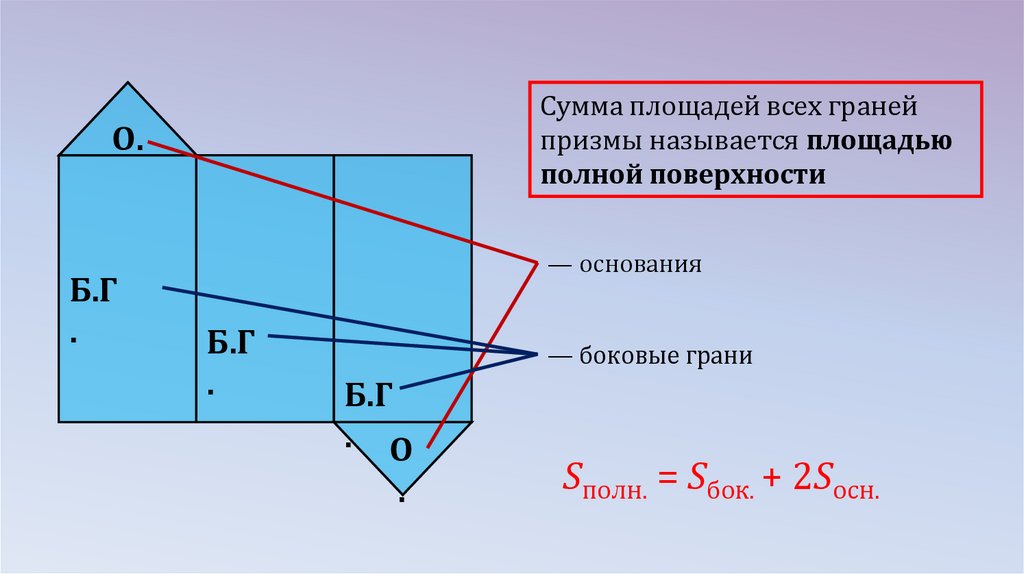
Сумма площадей всех граней
призмы называется площадью
полной поверхности
О.
Б.Г
.
— основания
Б.Г
.
— боковые грани
Б.Г
. О
.
Sполн. = Sбок. + 2Sосн.

12.

Теорема
Площадь боковой поверхности прямой призмы равна
произведению высоты призмы на периметр её основания
Sбок. = a1 · h + a2 · h + a3 · h + … an · h =
h
a3
a1
a2

13.

Объем призмы

14.

Правильные призмы

15.

Таблица вычисления площадей
правильных призм

16.

Решение задач

17.

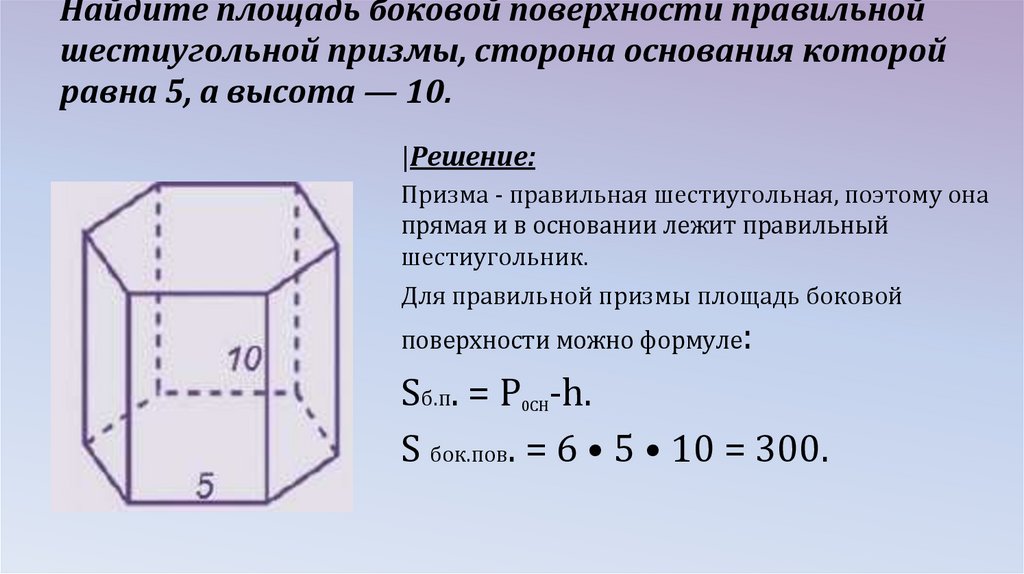
Найдите площадь боковой поверхности правильной
шестиугольной призмы, сторона основания которой
равна 5, а высота — 10.
|Решение:
Призма - правильная шестиугольная, поэтому она
прямая и в основании лежит правильный
шестиугольник.
Для правильной призмы площадь боковой
поверхности можно формуле:
Sб.п. = P -h.
S бок.пов. = 6 • 5 • 10 = 300.
0CH

18.

Основанием прямой треугольной призмы служит прямоугольный
треугольник с катетами 6 и 8. Площадь ее поверхности равна 288.
Найдите высоту призмы.

19.

СПАСИБО ЗА ВНИМАНИЕ