mat

1.

Тема урока:

2.

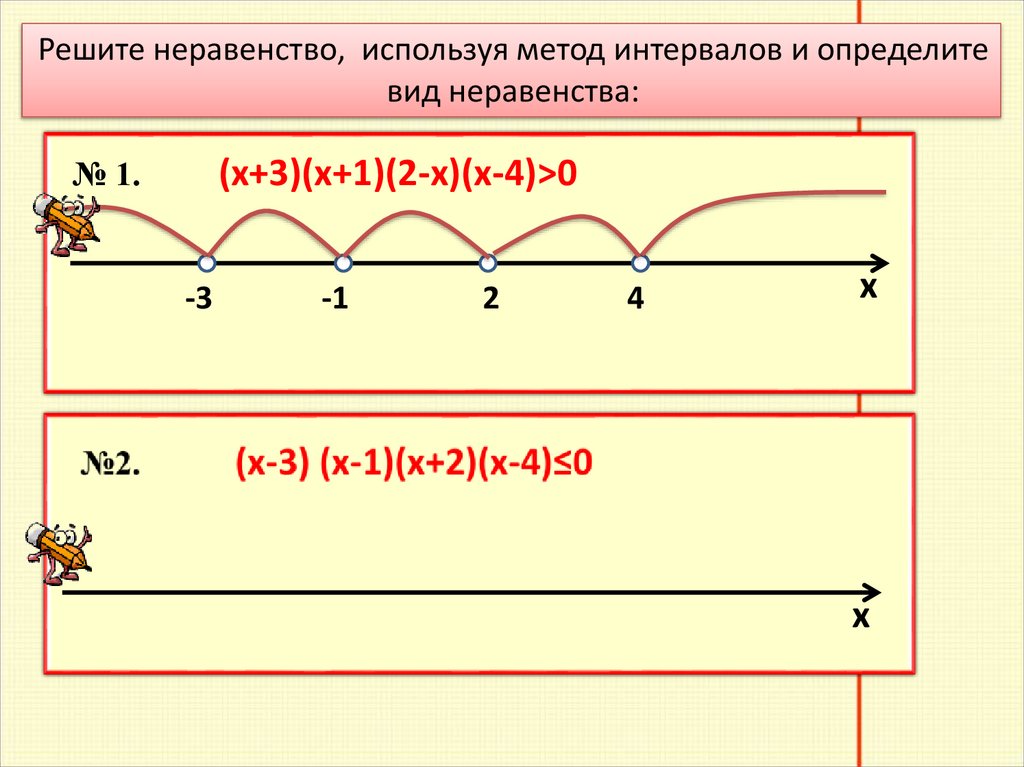
Решите неравенство, используя метод интервалов и определите
вид неравенства:
№ 1.
(х+3)(х+1)(2-х)(х-4)>0
-3
-1
2
4
x
x

3.

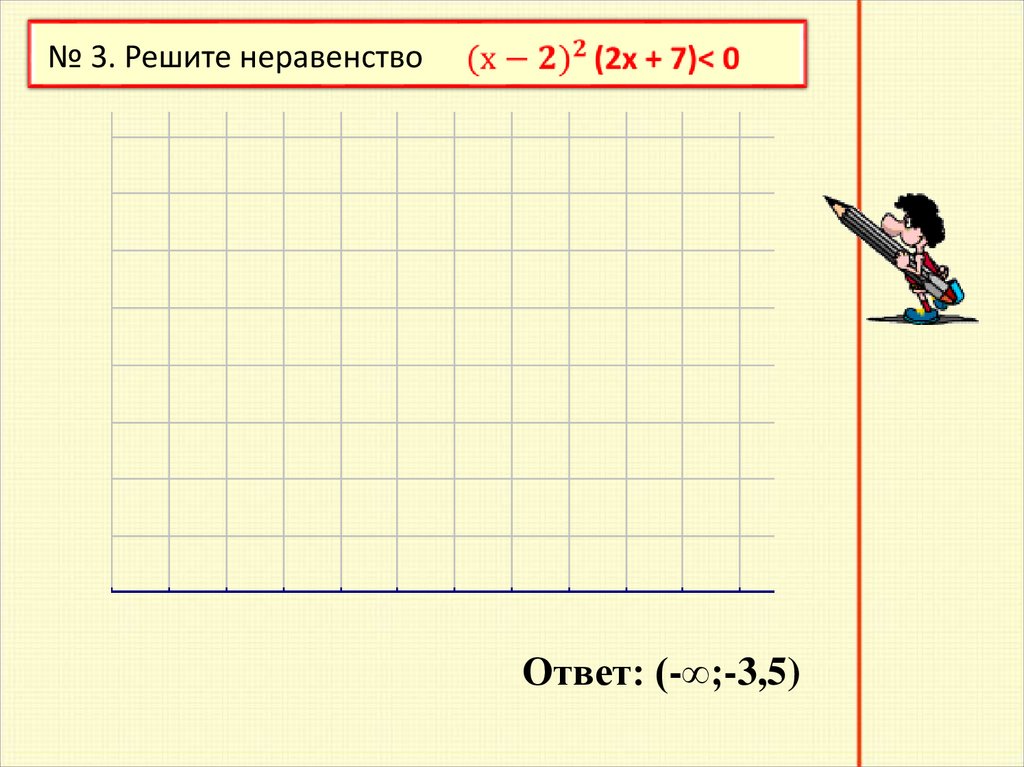
№ 3. Решите неравенство
8
6
4
2
-10
-5
Ответ: (-∞;-3,5)
-2

4.

№ 4. Решите неравенство
+
+
-4
х 2
0
( x 4)( x 4)
-2
+
5
Ответ: ( 4; 2) (4; )
х

5.

Если надо найти все числа х, каждое из которых
есть решение одновременно всех данных
рациональных неравенств, то говорят, что надо
решить систему рациональных неравенств с
одним неизвестным х.
Для того чтобы решить систему рациональных
неравенств, надо решить каждое неравенство
системы, затем найти общую часть (пересечение)
полученных множеств решений – она и будет
множеством всех решений системы.

6.

Пример 1.
Решим систему
неравенств
( х 1)( х 5)( х 7 ) 0,
( x 2 )( x 3)
0.
x 4
Решение
( х 1)( х 5 )( х 7 ) 0 ,
( х 2 )( х 3)( х 4 ) 0 .
+
-
-
IIIIIIIIIII1
-
+
5IIIIIIIIIIIIII7
+
2IIIIIIIII 3
-
х
+
4IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII X
Ответ: (5; 7)

7.

Пример 2.
Решение
2
x
6 x 10 0,
Решить систему
9
неравенств
x x3 x 2
0.
4
2
x x 1
Значит первое неравенство системы не имеет решения.
Теперь можно не решать второе неравенство системы,
так как ответ ясен: система неравенств не имеет
решений.
Ответ: нет решений.

8.

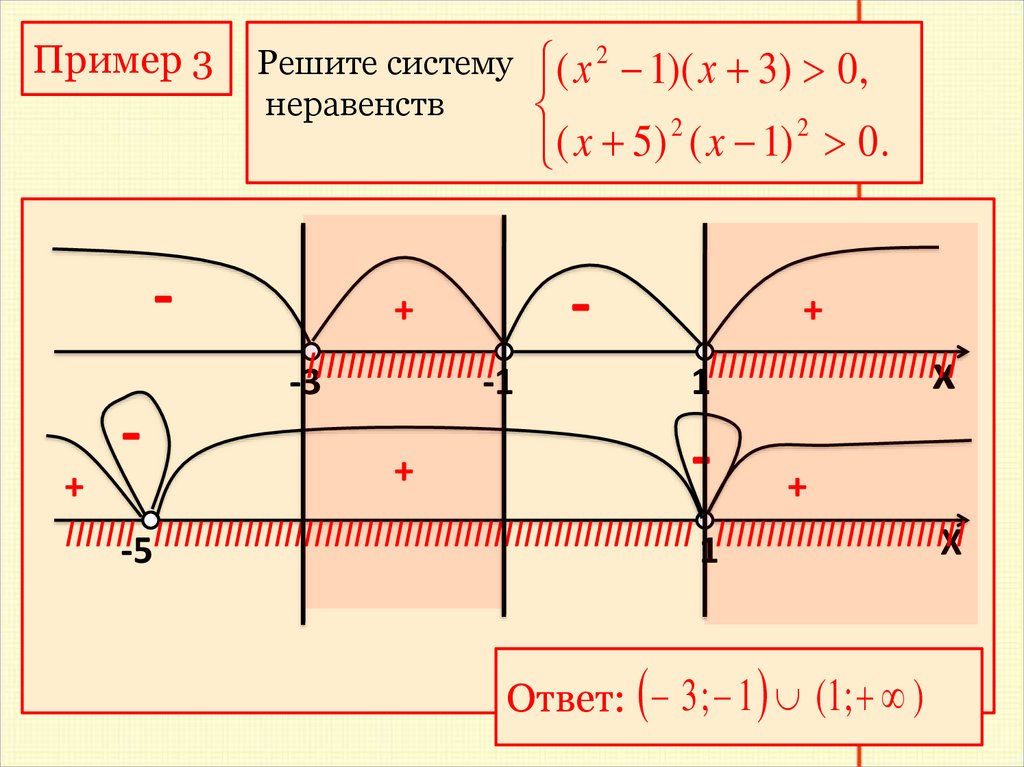
Пример 3
2
Решите систему
(
х
1)( х 3) 0,
неравенств
( x 5) 2 ( x 1) 2 0 .
-
+
-3IIIIIIIIIIIIIIIIIII-1
+
-
+
х
1IIIIIIIIIIIIIIIIIIIIIIIII
-
+
+
IIIIIII-5IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII 1IIIIIIIIIIIIIIIIIIIIIIIII
X
Ответ: 3 ; 1 (1; )

9.

Домашнее задание: