Неравенства и системы неравенств с двумя переменными

1. Неравенства и системы неравенств с двумя переменными

2. Девиз урока

Да, надо математику любить
И не считать ученье за мученье!
Все в жизни пригодится, ты учись,
Учись и не жалей на то мгновенье!

3.

Опишите графическую модель уравнения
у х 2х 5
ху 1
2
у х 0
2
х у 25
2
2
у х
2 х 3 у 15
( х 10) у 16
2
2
у х 12 0
2
y x
3
у 3
( х 5) ( у 3) 0
2
x 5
2

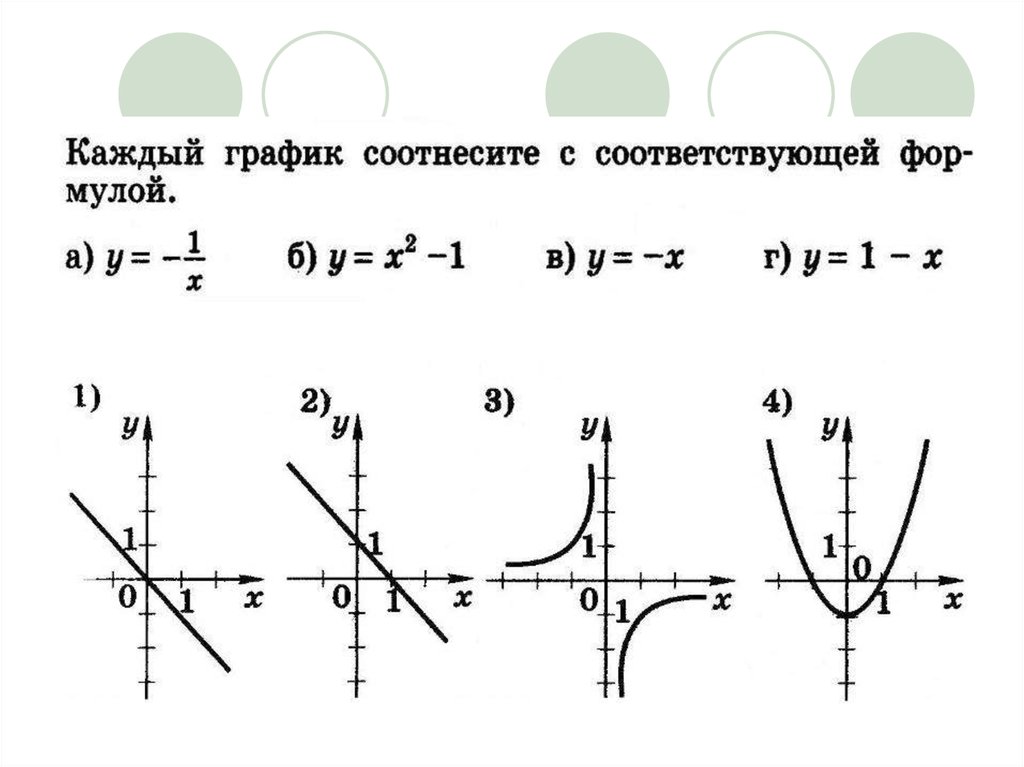
4.

5. Какая из пар (х; у) является решением

уравнения
неравенства
x 2y 0
2y x 0
а) (1; 2);
:
б) (2; 1)?

6. Решением какой системы уравнений является пара чисел (2;3)?

х у 13,
2 х у 7;
2
2
х у 5,
3
х
1
у
.
2

7. Какая из пар чисел (x;y) является решением системы неравенств

2x - 3y ≤ 6,
x + y + 7 >0:
а) (2;1)
б) (3;-2)?

8. Опишите алгоритм решения системы уравнений графическим методом

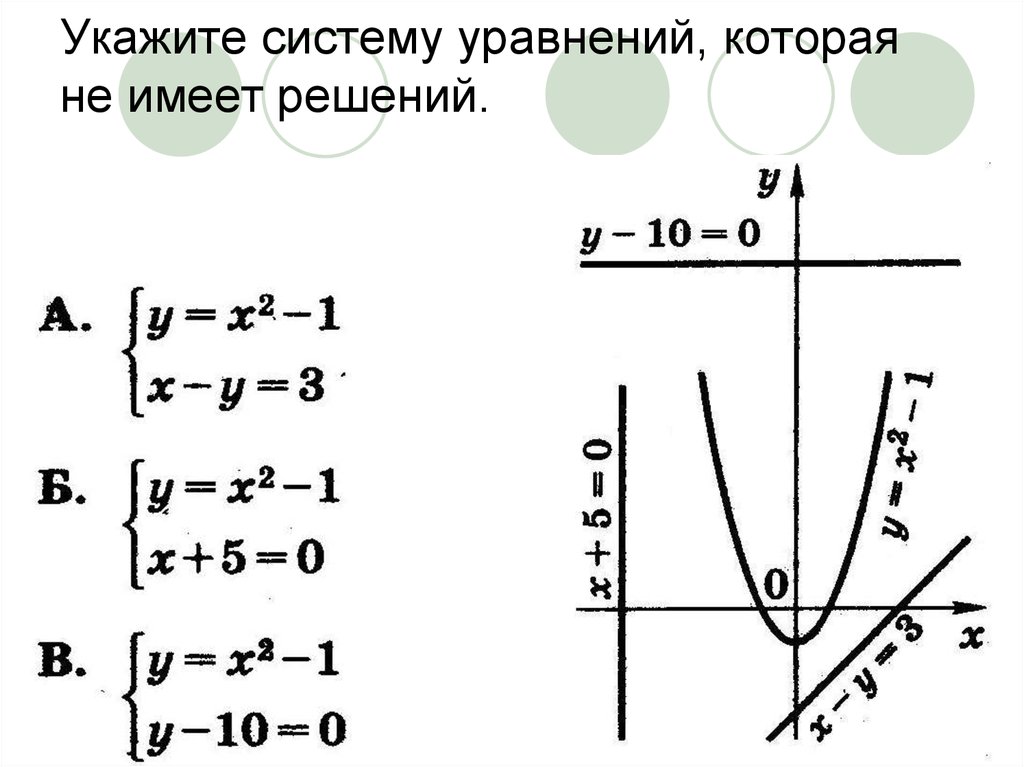
9. Укажите систему уравнений, которая не имеет решений.

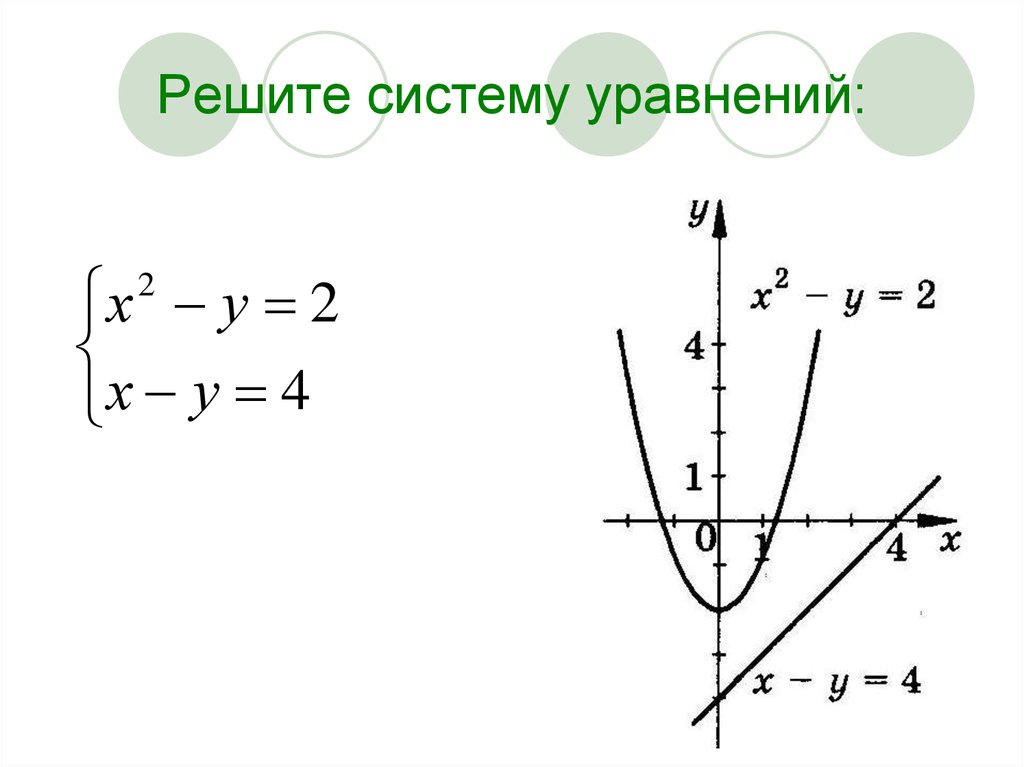
10. Решите систему уравнений:

х у 2
х у 4
2

11. Сколько решений имеет система уравнений?

4 у 3х 24
ху 12

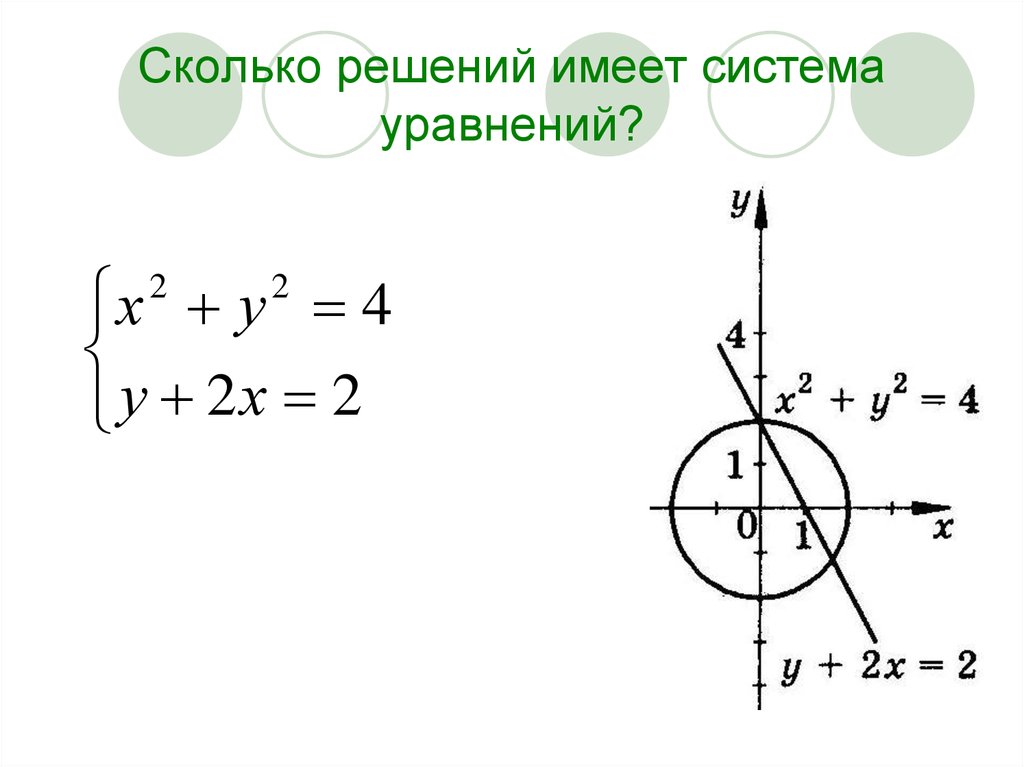
12. Сколько решений имеет система уравнений?

х у 4
у 2х 2
2
2

13.

Если уравнение р(х; у) = 0 удаётся преобразовать к виду
у = f(х), то график функции у = f(х) считается одновременно
графиком уравнения р(х; у) = 0. Полезно запомнить
соответствия:
Если координаты точки
то она лежит
К (х; у) удовлетворяют
соответственно
неравенству
у > f(х)
над линией
уравнению
у = f(х)
на линии
неравенству
у < f(х)
под линией
Обратное верно

14.

Решения неравенства изображаются точками плоскости,
расположенными по одну из сторон от графика уравнения. Чтобы
выбрать нужную часть плоскости, берут в какой-нибудь из них точку,
подставляют её координаты в заданное неравенство. Если
получается верное числовое неравенство, то часть плоскости
выбрана верно, если нет – то нет.
Если графиком рационального уравнения является линия L, то
по одну и по другую сторону от L выражение р(х; у) сохраняет
постоянный знак.

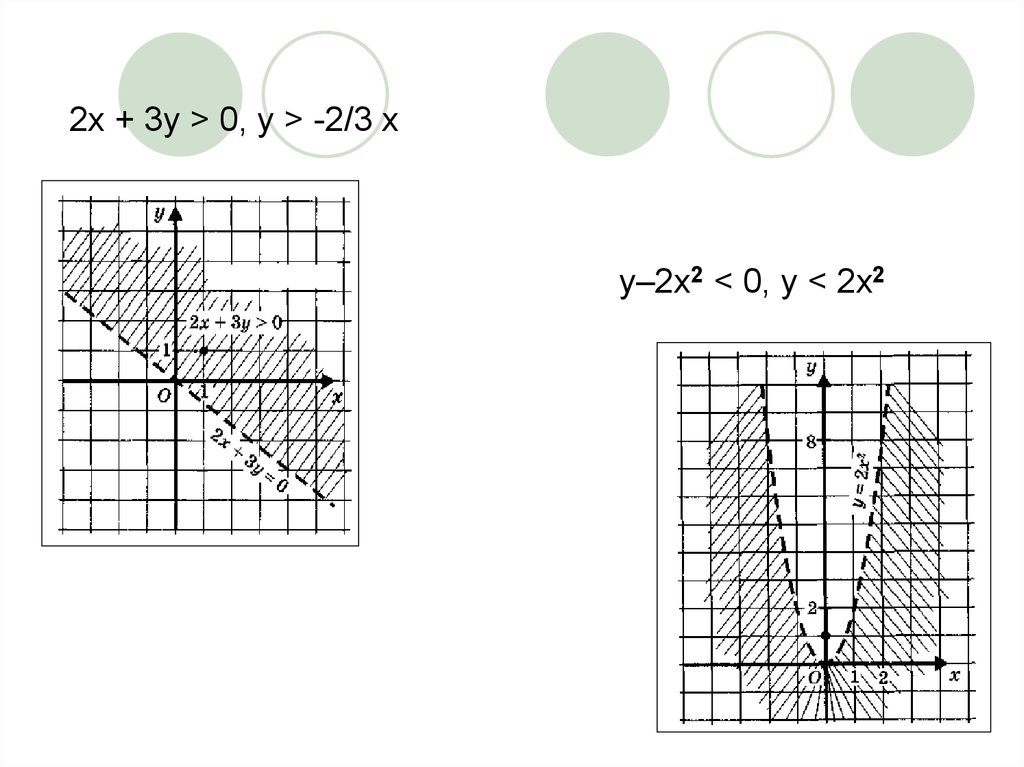
15.

2х + 3у > 0, у > -2/3 х
у–2х2 < 0, у < 2x2

16. Решите систему неравенств

2x – 3y ≤ 6,
x + y + 7 ≥ 0.

17. Математический диктант

18. Запишите аналитическую модель по данной геометрической.

1)
2)
3)

19. Запишите аналитическую модель по данной геометрической.

4)
5)
6)

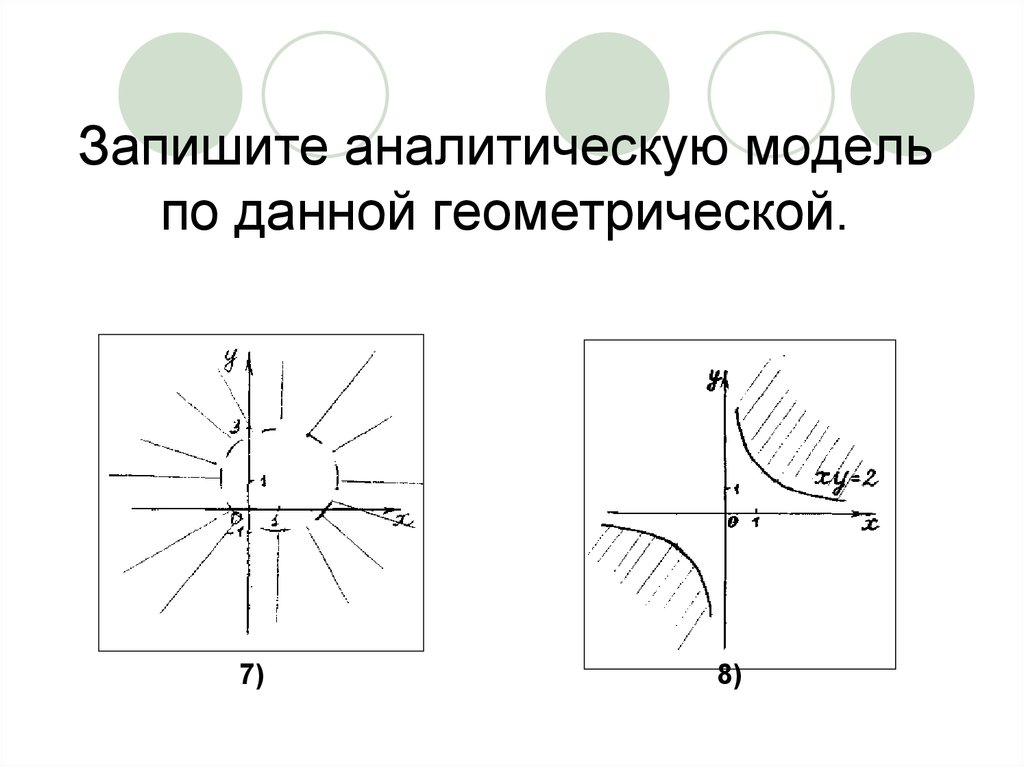
20. Запишите аналитическую модель по данной геометрической.

7)
8)

21. 9. Разбейте точки на три группы

D (0;3), Е (1;1), М (3;2)
А (2;2), В (4;0), С (-4;3)

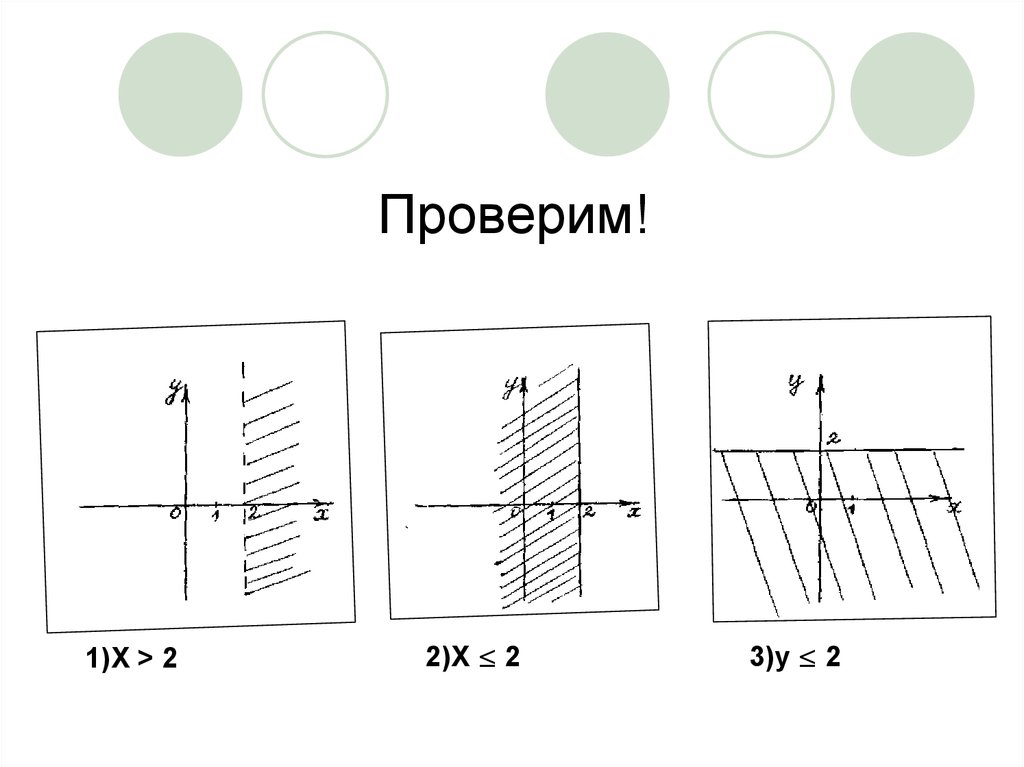
22. Проверим!

1)X > 2
2)X ≤ 2
3)y ≤ 2

23. Проверим!

4)y > -1
5)y ≥ x+1
6)x2 + y2 ≤ 16

24. Проверим!

7)(x-1)2 + (y-1)2 >4
8)xy ≥ 2

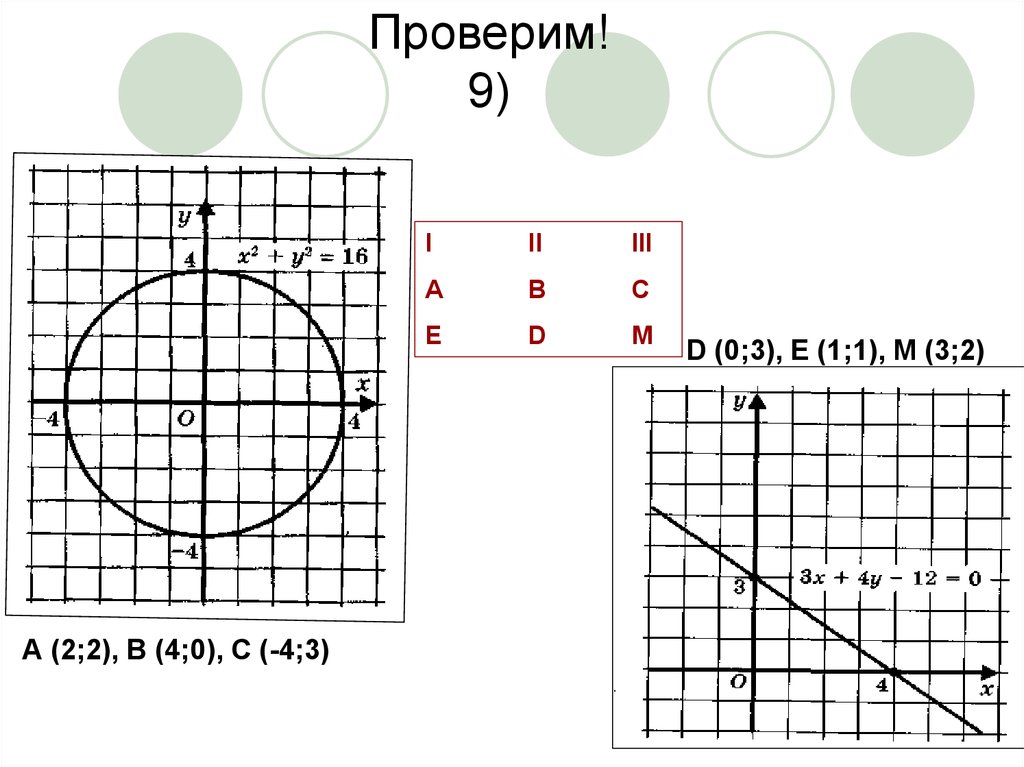
25. Проверим! 9)

А (2;2), В (4;0), С (-4;3)
I
II
III
A
B
C
E
D
M
D (0;3), Е (1;1), М (3;2)

26. Критерии оценки

Задания №1 - №4 – по 1 баллу
Задания №5 - №8 – по 2 балла
Задание №9 – 3 балла
Оценка «5» - 14-15 баллов
Оценка «4» - 10-12 баллов
Оценка «3» - 8-9 баллов